详解语言模型NGram及困惑度Perplexity

      对于自然语言相关的问题，比如机器翻译，最重要的问题就是文本的序列时候不是符合我们人类的使用习惯，语言模型就是用于评估文本序列符合人类语言使用习惯程度的模型。

      语言模型所面临的最大难题。我们为了让机器能够理解或者是产生符合人类语言的语言序列，一种方式是制定一个规范的人类语言范式（规范），比如陈述句需要需要有主语谓语宾语组成，定语需要放在索要修饰的名词之前等等。但是人类语言在实际使用的时候往往没有那么死板的规定，人类语言对于字、词的组合具有非常大的灵活性·，同样的含义，可以有许多种不同的表达方式，甚至很多的“双关语”、“反语”是人类幽默表达的组成部分，如果完全按照字面意思理解可能会贻笑大方，故而要给一门语言制定一个完整的规则显然是不现实的。

那怎么办呢？

     当前的语言模型是以统计学为基础的统计语言模型，统计语言模型是基于预先人为收集的大规模语料数据，以真实的人类语言为标准，预测文本序列在语料库中可能出现的概率，并以此概率去判断文本是否“合法”，是能能被人所理解。如下例子

打个比方, 如果有这样一段话:

        "今天我吃了西红柿炒__ "

    对一个好的语言模型, 这句话后面出现的词是"鸡蛋"的概率可能是 30%, "土豆"的概率是 5%, "豆腐"的概率是 5%, 但"石头"的概率则应当几乎为零.显然，鸡蛋的概率更高，也更加符合人类的习惯和理解方式，石头的概率最低，因为人类的习惯不是这样子的，这就是语言模型最直观的理解。

      从语言模型的发展历史看吗，主要经历了三个发展阶段，Ngram语言模型，神经网络语言模型，循环神经网络语言模型。本节主要介绍一下Ngram语言模型。

简单地说，语言模型就是用来计算一个句子的概率的模型，也就是判断一句话是否是人话的概率？

那么如何计算一个句子的概率呢？给定句子（词语序列）

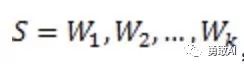
它的概率可以表示为：

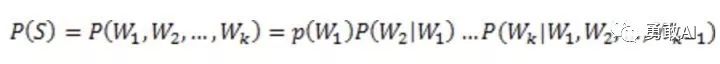
从上面可以看看出，因为W2的出现是与W1相关的，即在W1的条件下出现W2的概率，故而上述为一个条件概率的链式法则，而对于每一个词出现的条件概率，可以通过在语料库中统计计数的方式得出。

现在很多的应用中，需要计算一个句子的概率，一个句子是否合理，就看看它的可能性大小，这里可能性的大小就用概率来衡量。比如下面几个例子：

在机器翻译中：

P(high  winds  tonite)  >  P(large  winds  tonite)

拼写检查中：比如这一句话：The  office  is  about  fiIeen  minuets  from  my  house

显然 P(about  fiIeen  minutes  from)  >  P(about  fiIeen  minuets  from)

语音识别中：

比如I  saw  a  van 和eyes  awe  of  an听上去差不多，但是P(I  saw  a  van)  >>  P(eyes  awe  of  an)

上面的几个例子中都需要计算一个句子的概率，以作为判断其是否合理的依据。下面将上述的内容形式化描述。

我们需要计算一个句子或序列W的概率：

 P(W)  =  P(w 1 ,w 2 ,w 3 ,w 4 ,w 5 …w n )

其中我们也需要计算一个相关的任务，比如P(w 5 |w 1 ,w 2 ,w 3 ,w 4 )，表示w 1 w 2 w 3 w 4 后面是w 5的概率，即下一个词的概率。

像这样计算P(W)或者P(w n |w 1 ,w 2 …w n-­‐1 )  的模型叫做语言模型( language  model简称LM)。

那么如何计算P(W)呢？用概率的链式规则，链式规则常常用来评估随机变量的联合概率，链式规则如下：

将上面的链式规则计算P(W)可以写作如下：

按照链式规则计算方式，举例如下：

P(“its water is so transparent”) = P(its) × P(water|its) ×  P(is|its water) ×  P(so|its water is) ×  P(transparent|its water is so)

那么下面的问题是如何计算上面每一个概率，比如 P(transparent|its water is so)，一种比较直观的计算就是计数然后用除法：

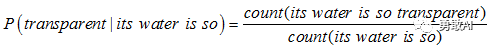
事实上不能用这种方式去计算条件概率，原因有两个：

1.直接这样计算会导致参数空间过大。一个语言模型的参数就是所有的这些条件概率，试想按上面方式计算P(w 5 |w 1 ,w 2 ,w 3 ,w 4 )，这里w i都有一个词典大小取值的可能，记作|V|，则该模型的参数个数是|V|^5，而且这还不包含P(w4 | w1, w2, w3)的个数，可以看到这样去计算条件概率会使语言模型参数个数过多而无法实用。

2.数据稀疏严重。我的理解是像上面那样计数计算，比如计数分子its water is so transparen,在我们所能见的文本中出现的次数是很小的，这样计算的结果是过多的条件概率会等于0，因为我们根本没有看到足够的文本来统计！

为什么呢？

对于第二个问题，假设一个语料库中单词的数量为|V|个，一个句子由n个词组成，那么每个单词都可能有|V|个取值，那么由这些词组成的n元组合的数目为|V|ⁿ  种，也就是说，组合数会随着n的增加而呈现指数级别的增长，随着n的增加，预料数据库能够提供的数据是非常有限的，除非有海量的各种类型的语料数据，否则还有大量的n元组合都没有在语料库中出现过（即由n个单词所组成的一些句子根本就没出现过，可以理解为很多的n元组所组成的句子不能被人很好地理解）也就是说依据最大似然估计得到的概率将会是0，模型可能仅仅能够计算寥寥几个句子。怎么解决呢？

为了解决參数空间过大的问题。引入了马尔科夫假设：随意一个词出现的概率只与它前面出现的有限的一个或者几个词有关。

上面的计算方式是通过马尔科夫假设进行简化的，马尔可夫假设是指假设第wi个词语只与它前面的k个词语相关，这样我们就得到前面的条件概率计算简化如下：

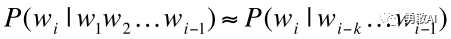
这样我们的P(W)计算简化如下：

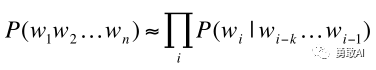
当k = 0时，这个时候对应的模型叫做一元模型(Unigram  model)，即wi与它前面的0个词相关，即wi不与任何词相关，每一个词都是相互独立的，P(W)计算如下：

当k = 1时，对应的模型叫做二元模型(Bigram  model)，此时wi与它前面一个词相关，P(W)计算如下：

同样的，我们可以让k = 2，叫做 trigrams，4-grams，5-grams，当k = N - 1，模型成为n元模型，即N-grams。

NGram的不足：

1. 总的来说，N-grams有一些不足，因为语言存在一个长距离依赖关系，比如考虑下面的句子：

2. “The      computer which I had just put into the machine room on the fifth floor      crashed.”

3. 假如我们要预测最后一个词语crashed出现的概率，如果采用二元模型，那么crashed与floor实际关联可能性应该非常小，相反的，这句子的主语computer与crashed的相关性很大，但是n-grams并没有捕捉到这个信息。

如果一个词的出现与它周围的词是独立的，那么我们就称之为unigram也就是一元语言模型：

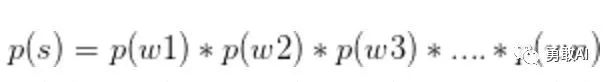
如果一个词的出现仅依赖于它前面出现的一个词，那么我们就称之为bigram：

假设一个词的出现仅依赖于它前面出现的两个词，那么我们就称之为bigram：

一般来说，N元模型就是假设当前词的出现概率只与它前面的N-1个词有关。而这些概率参数都是可以通过大规模语料库来计算，比如三元概率有：

在实践中用的最多的就是bigram和trigram了，高于四元的用的非常少，由于训练它须要更庞大的语料，并且数据稀疏严重，时间复杂度高，精度却提高的不多。

下面我们详细介绍一下一元语言模型，二元语言模型来帮助大家理解语言模型。

要计算出模型中的条件概率，这些条件概率也称为模型的参数，得到这些参数的过程称为训练。用最大似然性估计计算下面的条件概率：

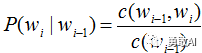
其中c(wi-1)表示wi-1出现的次数，是count的首字母c

一元语言模型中，我们的句子概率定义为：

,在这里，这个式子成立的条件是有一个假设，就是条件无关假设，我们认为每个词都是条件无关的。

那好，刚刚说了语言模型是得到一个句子的概率，此时我们句子的概率计算公式已经有了，那么如何估计

这些值呢？

     首先介绍一下，这里的参数种类是一种 P(wn),但是参数实例有V个（V是我们的词典大小）我们应该如何得到每个参数实例的值。用的是极大似然估计法。

比如我们说我们的训练语料是下面这个简单的语料。

那么我们的字典为：“星期五早晨，我特意起了个大早为的就是看天空。” 22个不同词，每个词语的概率直接用极大似然估计法估计得到。

如：p(星)=1/27，p(期)=1/27，一直算到后面的空为1/27.

于是我们就需要存储我们学习得到的模型参数，一个向量，22维，每个维度保存着每个单词的概率值。

那么有同学就需要问了，来了一句话，我们应该怎么估计呢？下面我举一个简单的例子来模拟一下如何用语言模型估计一句话的概率，比如：

p(我看看早晨的天空)=p(我)*p(看)*p(看)*p(早)*p(晨)*p(的)*p(天)*p(空)=1/27*1/27*1/27*....*1/27就能够直接运算出来。

于是我们得出，只要将每句话拆开为每个单词然后用累积形式运算，这样我们就能算出每句话的概率来了。

但是这样是不是就解决我们所有的问题呢？并没有，下面我们介绍二元语言模型。

我们再看一个Bigram的例子，这个例子来自大一点的语料库，为了计算对应的二元模型的参数，即P(wi | wi-1)，我们要先计数即c(wi-1，wi)，然后计数c(wi-1)，再用除法可得到这些条件概率。可以看到对于c(wi-1，wi)来说，wi-1有语料库词典大小（记作|V|）的可能取值，wi也是，所以c(wi-1，wi)要计算的个数有|V|^2。c(wi-1，wi)计数结果如下:

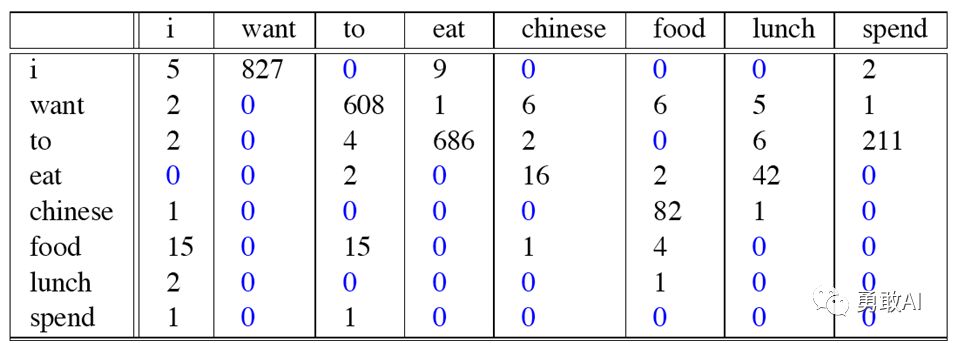
c(wi-1)的计数结果如下：

那么二元模型的参数计算结果如下：

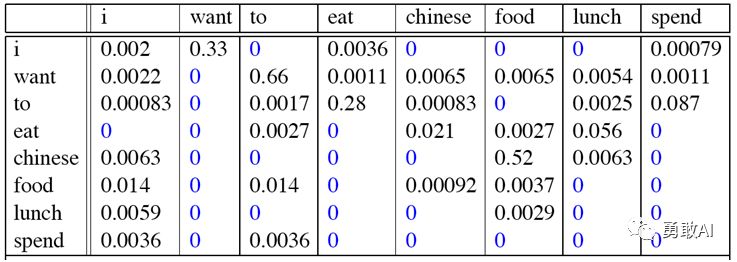
比如计算其中的P(want | i) = 0.33如下：

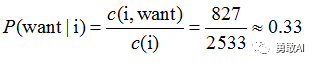
那么针对这个语料库的二元模型建立好了后，我们可以计算我们的目标，即一个句子的概率了，一个例子如下：

P(<s> I want english food </s>) = P(I|<s>) ×  P(want|I) × P(english|want) ×  P(food|english)  ×  P(</s>|food) =  .000031

这个数已经很小了

我们再看一下该二元模型所捕捉到的一些实际信息：

实际上常常在对数空间里面计算概率，原因有两个：

1. 1.防止溢出，可以看到，如果计算的句子很长，那么最后得到的结果将非常小，甚至会溢出，比如计算得到的概率是0.001，那么假设以10为底取对数的结果就是-3，这样就不会溢出。

2. 2.对数空间里面加法可以代替乘法，因为log(p1p2) = logp1 + logp2，而在计算机内部，显然加法比乘法执行更快！

什么是Perplexity(困惑度)?

“困惑度”这一概念最初的来源是信息论，在信息论中，perplexity(困惑度)用来度量一个概率分布或概率模型预测样本的好坏程度。它也可以用来比较两个概率分布或概率模型。（译者：应该是比较两者在预测样本上的优劣）低困惑度的概率分布模型或概率模型能更好地预测样本。可以从三个不同的方面去解释困惑度（殊途同归）

1.概率分布的困惑度 概率模型的困惑度 每个分词的困惑度

定义离散概率分布的困惑度如下：

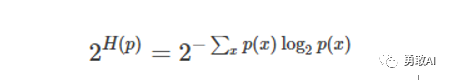 其中H(p)是概率分布p的熵，x是样本点。因此一个随机变量X的困惑度是定义在X的概率分布上的（X所有”可能”取值为x的部分）。（译者：x不能包含零测集的点，不然p(x)logp(x)没定义）

一个特殊的例子是k面均匀骰子的概率分布，它的困惑度

k。一个拥有k困惑度的随机变量有着和k面均匀骰子一样

的不确定性，并且可以说该随机变量有着k个困惑度的

值（k-ways perplexed）。（在有限样本空间离散随机

变量的概率分布中，均匀分布有着最大的熵）

困惑度有时也被用来衡量一个预测问题的难易程度。

但这个方法不总是精确的。例如：

在概率分布B(1,P=0.9)中，即取得1的概率是0.9

，取得0的概率是0.1。可以计算困惑度是：

同时自然地，我们预测下一样本点的策略将是：预测其取值为1，那么我们预测正确的概率是0.9。而困惑度的倒数是1/1.38=0.72而不是0.9。（但当我们考虑k面骰子上的均匀分布时，困惑度是k，困惑度的倒数是1/k，正好是预测正确的概率）

困惑度是信息熵的指数。

用一个概率模型q去估计真实概率分布p，那么可以通过测试集中的样本来定义这个概率模型的困惑度。

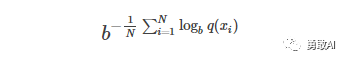
其中测试样本

我们指出，指数部分是交叉熵。

其中 p^p^ 表示我们对真实分布下样本点x出现概率的估计。比如用p(x)=n/N

在自然语言处理中，困惑度是用来衡量语言概率模型优劣的一个方法。一个语言概率模型可以看成是在整过句子或者文段上的概率分布。（译者：例如每个分词位置上有一个概率分布，这个概率分布表示了每个词在这个位置上出现的概率；或者每个句子位置上有一个概率分布，这个概率分布表示了所有可能句子在这个位置上出现的概率）

比如，i这个句子位置上的概率分布的信息熵可能是190，或者说，i这个句子位置上出现的句子平均要用190 bits去编码，那么这个位置上的概率分布的困惑度就是2^(190)。（译者：相当于投掷一个2^(190)面筛子的不确定性）通常，我们会考虑句子有不同的长度，所以我们会计算每个分词上的困惑度。比如，一个测试集上共有1000个单词，并且可以用7.95个bits给每个单词编码，那么我们可以说这个模型上每个词有2^(7.95)=247 困惑度。相当于在每个词语位置上都有投掷一个247面骰子的不确定性。

在Brown corpus (1 million words of American English of varying topics and genres) 上报告的最低的困惑度就是247per word，使用的是一个trigram model（三元语法模型）。在一个特定领域的语料中，常常可以得到更低的困惑度。

要注意的是，这个模型用的是三元语法。直接预测下一个单词是”the”的正确率是7%。但如果直接应用上面的结果，算出来这个预测是正确的概率是1/247=0.4%，这就错了。（译者：不是说算出来就一定是0.4%，而是说这样算本身是错的）因为直接预测下一个词是”the“的话，我们是在使用一元语法，而247是来源于三元语法的。当我们在使用三元语法的时候，会考虑三元语法的统计数据，这样做出来的预测会不一样并且通常有更好的正确率。

我们能够建立语言模型了，一般的我们在训练集上得到语言模型的参数，在测试集里面来测试模型的性能，那么如何去衡量一个语言模型的好坏呢？比较两个模型A,B好坏，一种外在的评价就是将AB放入具体的任务中，然后分别得到模型的准确率，这种方式当然是最好的方式，但这种方式的缺点是过于耗时，在实际情况中往往需要花费过多时间才能得到结果。另一种方式是使用下面要介绍的困惑度，但注意困惑度并不是上述外在评价的一个好的近似，所以一般使用在试点试验上，所谓试点试验就是一个小规模的初步研究，以评估一些性能。

困惑度

困惑度的基本评价方式是对测试集赋予高概率值的模型更好，一个句子W的困惑度(PP)定义如下：

对于二元模型，该公式为：

可以看到，概率越大，困惑度越小，即小的困惑度等于好的模型。且当wi之间是独立的（一元模型），且等概率为p时，公式为：

比如计算一个只包含0~9数字序列的困惑度，每个数字发生的概率是1/10。那么我们得到困惑度PP(W) = 10。这里讲义并没有详细的讲一个测试集上的困惑度是如何定义的，需要一些信息论的概念。

这节的核心就是句子概率越大，语言模型越好，迷惑度越小。

深度学习之前，传统的基于统计算法的语言模型，在测试时困惑度大多都在 80以上 (人工语言处理的困惑度的理论最低点大约在 10-20 之间)．一方面是算法的局限，另一方面是来自培训语句数量规模的限制.

2013年，以 Ciprian Chelba 为首的来自谷歌的团队推出了一个叫做＂十亿单词基准＂(Ｏne Billion Word Benchmark) 的语料库．这个语料库包含了接近十亿个英文单词组成的不同语句, 用来培训和测试不同的算法模型. 这个数据规模, 是先前流行的所谓 "Penn Treebank" 的包含四百五十万英文单词的语料库的大约两百倍.

Chelba 的团队, 使用一个包含二百亿个自由参数的循环神经网络的模型, 模型的训练消耗了十天的时间, 把困惑度下降到了 51 左右. (同期使用传统的统计算法, 最佳结果是 67)

2016年二月, 以 Rafal Jozefowicz 为第一作者的谷歌大脑的团队, 发表论文, "探索语言模型的极限" (Exploring the limits of language modeling). 该团队, 使用了 RNN/ LSTM 和所谓 "字母层面的卷积神经网络" (Character-Level Convolutional Neural Network) 的技术结合的模型, 在"十亿单词基准"的测试上把困惑度降低到了 30. 而相应的模型自由参数的数目降到了只有十亿 (相当于 Chelba 团队的模型的百分之五), 计算量大大降低.

更有意思的是,当把十个经过微调的不同参数的LSTM模型综合起来,取其均值, 对测试数据验证时, 其困惑度最低达 23.7.

机器越来越懂人话, 越来越会说人话了.