014基于深度学习的脑电癫痫自动检测系统-2018(300引用)_心电信号窗口

An automated system for epilepsy detection using EEG brain signals based on deep learning approach

 a b s t r a c t 

癫痫是一种威胁生命和具有挑战性的神经系统疾病，影响着世界各地的大量人群。对于其检测，脑电图(EEG)是一种常用的临床方法，但人工检查EEG脑信号是一个费时费力的过程，给神经科医生带来了沉重的负担，影响了他们的工作表现。已经提出了几种使用传统方法来帮助神经科医生的自动系统，这些系统在检测二元癫痫情况(例如正常对发作)时表现良好，但是在分类三元情况(例如发作对正常与发作间期)时性能下降。为了克服这个问题，我们提出了一个系统，它是金字塔一维卷积神经网络(P-1D-CNN)模型的集成。虽然CNN模型学习数据的内部结构，并且优于手工设计的技术，但主要问题是大量可学习的参数，这些参数的学习需要大量的数据。为了克服这个问题，P-1D- CNN致力于细化方法的概念，与标准CNN模型相比，它涉及的参数减少了61%，因此具有更好的通用性。为了进一步克服少量数据的限制，我们提出了两种增强方案。我们在基准数据集波恩大学数据集上测试了该系统；在几乎所有与癫痫检测相关的情况下，它的准确率为99.1±0.9%，优于最先进的系统。此外，在享有CNN模型的优势的同时，P-1D-CNN模型需要少61%的存储空间，并且其检测时间非常短(< 0.0 0 0481 s)，因此其适合于实时临床设置。这将减轻神经科医生的负担，并有助于患者在癫痫发作前提醒他们。提出的P-1D- CNN模型不仅适用于癫痫检测，而且可以用于开发针对其他类似疾病的健壮专家系统。

1. Introduction

癫痫是一种神经系统疾病，影响着全球约5000万人(Megiddo et al.， 2016)。脑电图(EEG)是一种有效的非侵入性技术，通常用于监测大脑活动和癫痫的诊断。脑电图读数由神经学家分析，以检测和分类疾病的模式，如发作前期和癫痫发作。目测费时费力;检查一个病人一天的脑电图记录需要很多小时，而且需要专家的服务。因此，对患者脑电图脑信号的分析给神经科医生带来了沉重的负担，降低了他们的工作效率。这些限制促使人们努力设计和开发自动系统，以帮助神经学家对癫痫和非癫痫脑电图脑信号进行分类。

最近，人们开展了大量的研究工作来将癫痫和非癫痫信号分类(Gardner，Krieger，Vachtsevanos，&Litt，2006；Meier，Dittrich，Schulze-Bonhage，&Aertsen，2008；Mirowski，Madhavan，LeCun，&Kuzniecky，2009；Sheb&Guttag，2010)。从机器学习的角度来看，癫痫和非癫痫脑电信号的识别是一项具有挑战性的任务。通常，由于癫痫发作的罕见，有少量的癫痫数据可用于训练分类器。此外，数据中噪声和伪影的存在造成了学习与正常、发作和非发作病例相关的大脑模式的困难。由于患者的癫痫形态不一致，这一难度进一步增加(McShane，2004)。现有的癫痫发作自动检测技术使用传统的信号处理(SP)和最大似然技术。其中许多技术对一个问题表现出很好的准确性，但对其他问题却不能准确执行。他们对癫痫发作和非癫痫发作病例进行分类的准确性很好，但在正常发作与发作间歇期的情况下表现较差(Zhang，Chen，&Li，2017)。由于三个原因，它仍然是一个具有挑战性的问题：1)不存在可以将二进制和三元问题分类的广义模型(即正常vs.发作vs.发作间期)，ii)较少可用的标记数据，以及iii)低准确度。为了帮助和辅助神经学家，我们需要一种通用的自动系统，即使使用较少的训练样本也能提供良好的性能(Andrzejak等人，2001；Sharmila&Geethanjali，2016)。

现有的检测癫痫发作的方法使用手工设计的技术从脑电信号中提取特征。一些方法使用来自EEG信号的信息的频谱(Tzallas等人，2012)和时间角度(Shoeb，2009)。脑电信号包含具有长时间周期的低频特征和具有短时间周期的高频特征(Adeli，周和爸爸-Mehr，2003)，即特征之间存在一种层次。深度学习是一种先进的最大似然学习方法，它自动编码特征的层次结构，这些特征不依赖于数据，并适应数据的内部结构，在许多应用中显示了良好的结果。此外，使用DL模型提取的特征被证明比手工设计的特征更具区分性和健壮性(LeCun&Bengio，1995)。为了提高癫痫和非癫痫脑电信号分类的准确性，提出了一种基于DL的分类方法。

最近出现的数字图书馆技术在几个应用领域表现出了显著的性能。深度CNN的变种，即。2D CNN如AlexNet(Krizevsky，Sutskever，&Hinton，2012)、VGG(Simonyan&Zisserman，2014)等或3D网络如3D CNN Ji，Xu，Yang，&Yu，2013)，C3D(Tran，Bourdev，Fergus，Tor-resani，&Paluri，2015)等在许多领域都表现出色。最近，1D-CNN已经成功地用于文本理解、音乐生成和其他时间序列数据(Cui，Chen，&Chen，2016；Ince等人，2016；LeCun，Bottou，Bengio，&Haffner，1998；Zhang&LeCun，2015)。DL方法的端到端学习范式避免了为提取和选择最具区分性的特征而选择适当的特征抽取器和特征子集选择器的适当组合，这些特征将由合适的分类器分类(Andrzejak等人，2001；Hussain，Aboalsamh，Abdul，Bamatraf和Ullah，2016；Sharmila&Geethanjali，2016；Zhang等人，2017)。虽然传统的学习方法训练速度快于动态学习方法，但在测试时速度慢得多，不能很好地推广。经过训练的深度模型可以在几分之一秒内对样本进行测试，适合于实时应用，唯一的瓶颈是需要大量的数据和较长的训练时间。为了克服这一问题，需要引入一种增强方案，该方案可以帮助以最佳方式使用少量可用数据来训练深度模型。

由于脑电记录是一维信号，我们提出了一种金字塔状的1D-CNN(P-1D-CNN)模型来检测癫痫，该模型包含的可学习参数要少得多。由于可用的数据量很小，因此，为了训练P-1D-CNN，我们提出了两种增强方案。使用训练好的P-1D-CNN模型作为专家，设计了一个P-1D-CNN模型集成系统，该系统采用多数投票策略融合局部决策来检测癫痫。该系统提取一个EEG信号，用固定大小的滑动窗口对其进行分割，并将子信号传递给基本P-1D-CNN模型(图2)，由P-1D-CNN模型对其进行处理，并将局部决策传递给多数投票模块。最后，多数票模块作出最终决定(图1)。在不同的癫痫检测问题上，它的表现优于最先进的技术。本研究的主要贡献是：(1)数据增强方案，(2)基于P-1D-CNN深层模型集成的二值和三值脑电信号分类的自动系统，(3)构造深层1D-CNN模型的新方法，(4)对用于检测不同癫痫病例的增强方案和深层模型进行全面的评价。

 

 

论文的其余部分安排如下：在第二节中，我们介绍了文献综述。第三节详细介绍了拟议的制度。第四节讨论了P-1D-CNN模型的模型选择、数据增强方案和训练。第五节介绍了结果；第六节讨论了结果，并将它们与最先进的方法进行了比较。最后，第六部分对全文进行了总结，并对未来的研究方向进行了展望。

2. Literature review 文献综述

癫痫和非癫痫脑电信号的识别是一个分类问题。该方法从脑电信号中提取识别特征，然后进行分类。在接下来的几段中，我们概述了利用不同的特征提取和分类方法对癫痫和非癫痫脑电图信号进行分类的相关技术。

几乎所有现有的癫痫检测方法都是基于手工设计的特征提取技术。Chua、Chandran、Acharya和Lim(201)使用高阶光谱(HOS)和基于功率谱的特征自动检测癫痫。采用高斯混合模型(GMM)作为分类器，基于HOS和功率谱特征的分类准确率分别为93.1 1%和88.78%。在另一项研究中，Chua、Chandran、Acharya和Lim(2009)使用基于HOS特征的SVM分类器，准确率达到92.67%。Acharya, Vinitha Sree和Suri(2011)使用累积量自动检测癫痫。他们从小波包分解(WPD)系数中提取HOS累积量，SVM分类器准确率达到98.5%。

Subasi(2007)提出了一种分类正常和癫痫脑电图脑信号的方法。该方法采用离散小波变换(DWT)将脑电信号分解为不同的频率子带。从DWT系数中提取四个统计特征，并传递到模块化神经网络(称为专家- mes混合)进行分类。他们报告的敏感性为95%，特异性为94%，准确性为94.5%。在另一项研究中(Acharya et al.， 2012)，作者使用SampEn, ApEn和两相熵和模糊分类器;他们报告的特异性为100%，准确性为98.1%，敏感性为99.4%。Martis等人(2013)使用了来自内部时间尺度分解(ITD)和决策树分类器的特征。该方法的准确性为95.67%，特异性为99.50%，敏感性为99%。在(Acharya et al.， 2013)中，作者提出了一种将脑电图大脑信号自动分类为三种不同类别的方法，即ictal、normal和intertal。他们使用连续小波变换(CWT)进行特征提取，支持向量机作为分类器。结果表明，该方法准确率达96%。

Swami、Gandhi、Panigrahi、Tripathi和Anand(2016)提取了手工制作的特征，如香农熵、标准差和能量。他们使用通用回归神经网络(GRNN)分类器对这些特征进行分类，并获得了最大的准确率，即在Bonn数据集中，A-E(非发作vs.发作)和AB-E(正常vs.发作)病例的准确率分别为10%和99.18%。然而，其他病例如B-E、C-E、D-E、CD-E和ABCD-E的最大准确率为98.4%。在另一项研究中，Guo、Rivero、Do- rado、Rabunal和Pazos(2010)在同一数据集上对ABCD-E病例实现了97.77%的准确性。他们使用人工神经网络分类器(ANN)对离散小波变换(DWT)提取的线长特征进行分类。Nicolaou和Georgiou(2012)从脑电图信号中提取排列熵特征。他们采用支持向量机(SVM)作为分类器，对波恩大学数据集上的a - e案例实现了93.55%的准确率。其他病例如B-E、C-E、D-E、ABCD-E的最大准确率为86.1%。Gandhi、Panigrahi和Anand(201)利用小波变换从EEG信号中提取熵、标准差和能量特征。他们使用支持向量机和概率神经网络(PNN)作为分类器，报告了ABCD- E病例的最大准确率为95.44%。Gotman, Ives和Gloor(1979)使用了锐波和尖刺识别技术。他们在Gotman(1982年、1999年)、Koffler和Gotman(1985年)和Qu和Gotman(1993年)中进一步加强了这种技术。Shoeb(2009)使用支持向量机分类器，采用患者特异性预测方法;结果表明，该方法的准确率达96%。在大多数工作中，用于区分发作和非发作事件的常用分类器是支持向量机(SVM)。然而，在Khan、Rafiuddin和Farooq(2012)的研究中，线性判别分析(LDA)分类器被用于对包括65例癫痫发作的5个受试者进行分类。该方法的准确性、灵敏度和特异性分别为91.8%、83.6%和10%。Acharya等人(2012)专注于使用熵值进行脑电图癫痫检测和七种不同的分类器。表现最好的分类器是Fuzzy Sugeno分类器，它达到了99.4%的灵敏度，10%的特异性和98.1%的整体准确性。表现最差的分类器是朴素贝叶斯分类器，其灵敏度为94.4%，特异性为97.8%，准确性为88.1%。Nasehi和Pourghassem(2013)使用粒子群Op- timization神经网络(PSONN)，其灵敏度为98%。

Yuan、Zhou、Liu和Wang(2012)使用极限学习机(ELM)算法进行分类。21(21)条截获记录用于训练分类器，65(65)条用于测试。结果表明，该系统的灵敏度平均为91.92%，特异性为94.89%，总体准确率为94.9%。Patel、Chua、Fau和Bleakley(2009)提出了一种低功率的实时分类算法，用于检测动态脑电图中的癫痫发作。他们比较了Mahalanobis判别分析(MDA)，二次判别分析(QDA)，线性判别分析(LDA)和支持向量机分类器对13(13)个主题。结果表明，当LDA在单个患者身上进行训练和测试时，效果最好。该方法的灵敏度为94.2%，特异性为77.9%，总体准确性为87.7%。当应用于所有受试者时，其灵敏度为90.9%，特异性为59.5%，总体准确性为76.5%。Acharya、Faust、Kannathal、Chua和Laxminarayan(2005)使用复发量化分析(RQA)特征对EEG信号进行三类分类，以检测癫痫。采用支持向量机作为分类器，以RQA参数为特征，准确率达到95.60%。此外，一个详细的特征提取器和分类器用于二进制(例如。Sharmila和Geethanjali(2016)和Zhang等人(2017)给出了癫痫vs非癫痫)和三元(癫痫vs正常vs间歇性)场景。

对上述最新的特征提取技术的概述表明，大多数特征提取技术都是手工设计的，并不通过学习数据的内部结构来从脑电图信号中提取辨别性信息;它们的性能取决于各种参数的调优，不能很好地泛化。为了提高癫痫检测系统的准确性和广泛性，可以使用DL方法来避免手工设计特征提取器和分类器的需要。据我们所知，目前还没有人使用DL方法进行癫痫检测，可能是因为现有数据量较少，不足以训练出一个深度模型。因此，我们有动机使用DL技术来提出一个包含少量可学习参数的深度模型，并有效地将脑电图大脑信号分为癫痫性和非癫痫性。然而，最近DL也被应用于类似的问题。Acharya等人(2017 a, b,c)最近将DL应用于从心电图信号中检测心律失常、心肌梗死和冠状动脉。他们使用了一个有11层的深度卷积神经网络模型。在Acharya等人(2017a)中，作者提出了两个CNN模型:A和B。模型A以一个包含500个样本的心电信号窗口作为输入，而模型B的输入是一个大小为1250个样本的窗口。我们的CNN模型与这些模型的不同之处在于:(1)它所涉及的层数较少(只有5层)，(2)它是基于金字塔结构的，显著减少了参数的数量。我们的系统是一个CNN模型的集合，它分析输入信号的不同部分，通过这种方式增加多样性，从而获得更好的检测性能。

3. The proposed system

基于P-1D-CNN模型集合的脑电图脑信号自动癫痫检测系统如图1所示。该系统由三个主要模块组成:(1)输入模块，将输入的脑电波信号分解成具有固定大小重叠窗口的子信号，并传递给P-1D-CNN基模型;(2)集合模块，子信号按P-1D-CNN基模型进行分类;(3)融合决策，采用多数投票的方法对局部决策进行融合，得出最终决策。

 

标准的深度CNN模型需要大量的数据进行训练，但对于癫痫检测问题，数据量是有限的。为了解决这个问题，我们在第4节中介绍了用于为训练基地P-1D-CNN模型创建数据的数据增强方案。

训练P-1D-CNN模型后，使用其副本作为基础模型，我们构建一个深度集成分类器，其中每个基础模型扮演检查输入信号不同部分的专家的角色。当输入信号传递给集合进行分类时，为了多样性(考虑到增强方法)，它被分割成重叠的窗口，然后传递给集合中不同的P-1D-CNN基模型，如图1所示，即信号的不同部分被分配给不同的专家(基模型)进行局部分析。经过局部分析，每个模型给出局部决策;最后，采用多数投票的方式将这些决策进行融合，形成最终决策。集合中P- 1D-CNN模型(专家)的数量取决于窗口的数量。例如，如果一个输入的脑电图信号被分成n个窗口(子信号)，集合将由n个P-1D- CNN基模型组成。我们用n = 3和n = 5测试了系统，发现n = 3给出了更好的结果

该系统的核心组件是一个P-1D-CNN模型。它是一个深度模型，由三种主要类型的层组成:卷积层(Conv)、批处理归一化层(BN)和全连接层(FC)。对于Conv和FC层，使用ReLU作为激活函数;Dropout技术用于训练中的正则化。ReLU和dropout采用不同的层进行应用，并在模型中得到一致的显示。在下一节中，我们将详细介绍这个深度模型。为了更紧凑地描述这些想法，表1给出了关键术语及其缩写。

3.1. P-1D-CNN architecture 架构

深层CNN模型(LeCun等人，1998；Simonyan&Zisserman，2014)从数据中自动学习EEG信号的结构，并以端到端的方式执行分类，这与传统的手动工程方法相反，在传统的人工工程方法中，首先提取特征，选择所提取的特征的子集，最后将其传递给分类器进行分类。CNN模型的主要组成部分是Conv层，它由许多通道(特征地图)组成。通道中每个神经元的输出是与输入信号上的固定感受场的核(由同一通道中的所有神经元共享)或前一卷积层的特征映射(1D信号)的卷积运算的结果。通过这种方式，CNN通过分析信号来了解不同信息的层次结构。在CNN中，核是从数据不同的手工工程方法中学习的，其中核是预定义的，例如。小波变换。

CNN具有共享内核的新颖思想，与完全连接的体系结构相比，它的优势在于显著减少了参数的数量。最近出现的使CNN更深入的方法增加了大量的参数，增加了它的复杂性，当可用数据集很小时，这是过拟合的潜在原因。现有的用于癫痫检测的脑电图数据集规模小，我们使用两种不同的策略来解决这一问题，即新的数据增强方案和包含少量参数的记忆高效深度金字塔CNN模型。

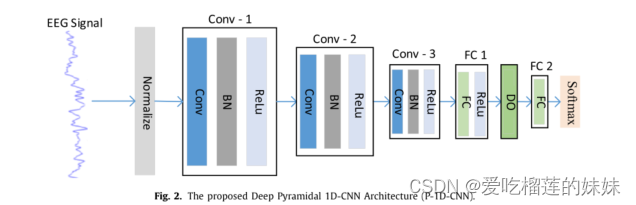
脑电图信号是一维时间序列;因此，我们提出了一个金字塔的1D-CNN模型，我们称之为P-1D-CNN，它的通用架构如图2所示，它是一个端到端模型。

 

与传统的CNN模型不同，它不包括任何池化层;通过在Conv层中使用更大的大步来减少冗余或不必要的特性。Conv和FC层从给定的输入信号中学习从低到高的特征层次。将具有语义表示的高级特征作为输入传递给最后一层的softmax分类器，预测输入脑电信号的各类。

CNN模型通常采用从过程到细化的方法，其中底层层包含少量的内核，而高层层包含大量的内核。但是这个结构包含了大量的可学习参数。它的复杂性很高。相反，我们采用了类似于Ullah和Petrosino(2016)为深度2D CNN提出的金字塔结构，即底层层有大量的内核，而高层层包含少量的内核。这种结构显著减少了可学习参数的数量，避免了过拟合的风险。在convv -1层取了大量的核，在convv -2和convc -3层取了一定数量的核，如表3所示的型号M5和M6，包括conv1、conv2和conv3层，分别有24、16和8个核。其思想是，低层次提取大量的微结构，这些微结构被更高层次的层组合成更高层次的特征，随着网络的深入，这些特征数量很少，但具有区别性，即该模型隐式地进行特征选择。

为了展示P-1D-CNN模型的有效性，我们考虑了8个不同配置的模型，其中4个基于金字塔结构。表3显示了这些模型的详细规格，并给出了每个模型中需要训练的参数数量。最后一层完全连接层有两个或三个神经元，这取决于脑电图大脑信号分类问题是两类(如癫痫和非癫痫)还是三类(正常、癫痫和间隔期)。在这些模型的帮助下，我们展示了一个适当设计的模型如何在较少参数的情况下产生相同或更好的性能，从而降低过拟合的风险。基于金字塔结构的模型涉及的可学习参数数量显著减少，见表3;例如，具有金字塔结构的模型M5的参数比类似的1D-CNN模型M1少61%。

深度P-1D-CNN模型(M5)的细节如图2所示。输入信号归一化为零的平均值和单位方差，即。

使用z分数归一化。这种归一化有助于更快的收敛和避免局部极小值。归一化输入由三个卷积块处理，每个卷积块由三层组成:卷积层、批处理归一化层(BN)和非线性激活层(ReLU)。conv1的核数为24个，每个核的感受野为5(即1 × 5);conv2的核数为16个，每个核的感受野为3(即1 × 3)，深度为24;conv3的核数为8，每个核的感受野为3(即1 × 3)，深度为16。第三个块的输出被传递给第一个FC层(FC 1)，然后是一个ReLU层和另一个FC层(FC 2)。

FC1中的神经元数量是20个。为了避免过拟合，我们在FC 2之前使用dropout层。将FC 2的输出交给一个softmax层，该层作为分类器，并预测输入信号的类别。FC2中的神经元数量是2或3，取决于类的数量。在测试时，模型不使用BN和DO。其他型号规格见表3。在接下来的小节中，我们将简要解释主要层，即1D-Conv层、BN层和FC层。详见LeCun et al.(1998)和Ioffe and Szegedy(2015)。

a) Convolution Layers

一维卷积运算用于滤波一维信号(如。时间序列)用于提取鉴别特征。将前一层与K个感知场Rf和深度c的核进行卷积生成Conv层，这些核等于前一层中的chan- nels或feature map的数量。形式上,卷积层X = {X ij: 1≤≤c j 1≤≤z},其中c是渠道的数量的层和z是神经元的数量在每个chan - nel与K内核K l, l = 1, 2,…,K的接受域卷积c产生射频和深度层Y = {Y lm: 1≤≤K, K m 1≤≤},在那里

m为该层每个通道中的神经元数量，K为该层中的通道总数。注意，生成的Conv层中的通道数量等于内核的数量。不同的核从输入信号中提取不同类型的判别特征。核的数量随着网络的深入而变化。底层核学习微观结构，而高层核学习高级特征。在该模型中，第一个Conv层选择最大的核数，并在随后的层中减少33%，以保持金字塔结构。三个Conv层的激活(通道)如图3所示。

 

a) Batch Normalization

在训练过程中，特征图的分布会因参数的更新而发生变化，这迫使选择较小的学习率和仔细的参数初始化。它减慢了学习的速度，使学习变得更加困难，因为饱和的非线性。Ioffe和Szegedy(2015)将这种现象称为内部协变量漂移，并提出了批量归一化(BN)作为解决这一问题的方法。在BN中，每一层的每个小批次的激活都是标准化的，详细信息可以在Ioffe和Szegedy(2015)中找到。现在，在神经网络中使用BN是非常普遍的。它有助于避免特殊的参数初始化，同时提供更快的收敛速度。在所提出的模型中，我们只在训练过程中的每一卷积层之后使用BN。

a) Fully Connected

在卷积层之后，每个模型有两个全连接(FC)层。CONV3层的所有神经元都被连接到每个神经元是第一个完全连接的层Fc1。在不同的模型中，Fc1内神经元的数量不同，详情如表3所示。第二个全连接层有2个或3个神经元，取决于检测问题，例如对于正常对癫痫问题，这是一个两类问题，FC2中的神经元数量是2，而对于正常对发作间期对发作，这是一个三类问题，FC2包含3个神经元。

4. Model selection and parameter tuning

首先，我们介绍了数据的细节，以及提出的数据增强方案。然后，我们给出了用于验证所提出的系统性能的评估指标。之后，对培训程序进行了详细的阐述。最后，最好的数据通过分析不同的数据增强方式和不同的一维CNN模型的结果，得出了P-1D-CNN模型和增强方案。

4.1. Dataset and data augmentation schemes

这项工作中使用的数据集由波恩大学的一个研究小组获得(Andrzejak等人，2001年)，并已被广泛用于癫痫检测的研究。使用标准的10-20电极放置系统记录脑电信号。完整的数据由五个集合(A到E)组成，每个集合包含100个单通道实例。A组和B组分别由5名健康志愿者在放松清醒状态下睁眼(A组)和闭眼(B组)时记录的脑电信号组成。C组、D组和E组记录自5名患者。D组脑电信号取自致痫灶。C组记录于对侧大脑半球的海马区。C组和D组包括在无癫痫发作间期(发作间歇期)测量的脑电信号，而E组的脑电信号仅在癫痫发作活动(发作)期间被记录(Andrzejak等人，2001年)。详情载於表二。

该数据集中收集的实例数量不足以训练有效的深度模型。为了解决这个问题，获取大量的脑电信号是不现实的，由专业神经学家对其进行标记也不是一件容易的任务。我们需要一种扩充方案来帮助我们增加足以训练深度广义CNN模型的数据量，这需要大量的训练数据才能获得更好的性能。现有的脑电信号数据量小，可以学习模型，但存在过度拟合的问题。为了克服这个问题，我们提出了两种数据增强方案来训练我们的模型。通过使用固定大小的窗口将给定的全长EEG信号分割成小信号来扩大数据；每个小信号被用作学习CNN模型的独立实例。将脑电信号分离成小信号是现有方法中采用的标准程序(Sharmila&Geethanjali，2016；Zhang等人，2017，Zhang等人，2017)。

波恩大学数据集中的每个记录由4097个样本组成。为了从一条记录中生成多个实例，我们采用了与参考文献中的方法类似的滑动窗口方法。Sharmila和Geethanjali(2016)和Zhang等人。(2017)。

在Zhang等人的研究中。(2017)，作者采用了窗口大小为512，步长为480(512的93.75%)；每条记录被分割成8个相等的脑电子信号，去掉最后一个样本。通过这种方式，从100个单通道记录中为每个数据集获得总共800个数据实例，但这个数量不足以学习深度模型。然而，这种方法表明大跨度没有帮助，可以使用较小的跨度来创建足够的数据。基于窗口大小和步长，我们提出了两种数据增强方案。

Scheme-1

将可用信号分为互不相交的训练集和测试集，分别占总信号的90%和10%。使用训练集来扩充数据。选择512的窗口大小和64的步长(512的12.5%，重叠87.5%)，将训练集中的长度为4097的每个信号分成57个子信号，每个子信号被视为独立的信号实例STR。这样，每个类别(类)总共创建5130个实例，用于训练P-ID-CNN模型。

为了进行测试，将测试集中的每个长度为4097的信号划分为4个子信号Sts，每个子信号的长度为1024，这些子信号被视为独立的测试信号实例。当长度为1024的信号实例Sts被传递到系统时，它被分成具有大小为512和50%重叠的窗口的三个子信号，即Sts i，i=1，2，3，每个大小为512，它们被传递到集合中的三个训练的基本P-ID-CNN模型，并且多数投票被用作融合策略以作出关于输入信号实例S的决策。集成中的每个基本模型充当专家的角色，独立分析信号实例Sts的局部部分，并在融合局部决策的帮助下由系统给出全局决策。

Scheme-2 

此方法类似于方案1。在这种情况下，用于创建训练实例S的窗口大小为512，重叠25%(即，步长128)。

为了测试，当长度为1024的输入信号实例Sts被传递到系统时，将其划分为具有大小为512和75%重叠的窗口的五个子信号，即，每个大小为512的Sts i，i=1，2，3，4，5，这些子信号被传递到集合中的五个经训练的基本P-ID-CNN模型，并且多数投票被用作融合策略以作出关于信号实例Sts的决定。

4.2. Performance measures (evaluation procedure)

在评估方面，我们采用了10次交叉验证，以确保系统在不同的数据变化上进行测试。每一类的100个信号被分成10个折叠，每个折叠(10%)依次保留用于测试，其余9个折叠(90%信号)用于学习模型。对于每个折叠，使用所提出的扩充方案和90%的训练数据来创建训练实例，并且从坚持的10%的测试数据来创建测试实例。平均性能计算为10倍。使用诸如准确度、特异度、敏感度、精确度、f-测量和g-均值等众所周知的性能指标来评估性能。大多数最先进的癫痫系统也使用这些指标，这些指标的适应评估我们的系统有助于与最先进的系统进行公平的比较。这些指标的定义如下：

其中，Tp(真阳性)是异常情况的数量(例如。FN(假阴性)是被预测为正常的异常病例的数量，TN(真阴性)是被预测为正常的正常病例的数量，FP(假阳性)是系统识别为异常的正常病例的数量。

Training of P-1D-CNN Model

P-1D-CNN的训练需要从数据中学习权重参数(核)。为了学习这些参数，我们使用了传统的具有交叉熵损失函数的反向传播技术和带有Adam优化程序的随机梯度下降方法(Kingma&BA，2014)。ADAM算法有六个超参数：学习率(0.001)，Beta1(0.9%)，Beta2(0.999)，Epsilon(0.0 0 0 1)，使用LOCKING(FALSE)和NAME(ADAM)；我们使用所有这些参数的缺省值(在括号中给出)，除了学习率，我们将其设置为一个非常小的数字0.0 0 0 2。虽然BN通常允许较高的学习率，但在使用ADAM优化器时，需要较小的学习率来控制网络的振荡，避免出现局部极小值问题。根据数据集的大小，用不同数量的迭代来训练模型。在Dropout中，所有实验的概率值均为0.5。该模型是在TensorFlow(TensorFlow，2017)中实现的，TensorFlow是谷歌的一个免费提供的DL库。每个实验的迭代次数不同--这取决于实验中使用的数据集的数量。例如，当我们使用两个数据集，即A与E或D与E时，我们以50k次迭代训练模型；当我们在实验中使用五个集合(即A、B、C、D或E)中的三个集合时，例如。

AB和C，我们将最大迭代次数设置为150k。然而，当我们使用四个或所有五个可用信号集时，我们用300k次迭代来训练我们的模型。虽然模型的训练速度要快得多，但我们仍然将其训练到指定的最大迭代次数，以便更好地泛化模型。

4.2.1. Selection of best model and data augmentation scheme

为了选择最好的模型，我们在最初的实验中考虑了八个CNN模型，如表3所示。对于最佳模型的选择，我们需要解决两个问题：(A)哪种数据增强方案最合适？(B)金字塔体系结构是否比传统模型有更好的普适性，传统模型的核心数量随着网络的深入而增加？为了回答这些问题，我们仅对三类问题：非癫痫发作(AB)与癫痫发作间期(CD)与癫痫发作(E)这三类问题，对所有八个模型进行了10倍交叉验证。这些实验使我们选择了最好的模型和数据增强方案，并将其用于其他分类问题。应该注意的是，所有10重交叉验证集都是随机创建的，强制将所有样本包括在训练(90%)和测试(10%)中。

模型的训练和测试使用数据增强方案1和2。模型M1到M4是使用随着网络的深入而在每个较高层增加K(过滤器或核的数量)的传统概念来设计的，而模型M5到M8(金字塔模型)是使用过程到精细化的概念来设计的，即随着网络的深入而减少K(过滤器或核的数量)33%的比例。

与传统模型相比，金字塔模型涉及的参数数量更少，因此不太容易过度拟合和很好地泛化。

表3给出了使用不同模型和数据增强方案的10倍交叉验证获得的平均性能结果。首先，使用数据增强方案1和2的平均精度(所有模型)及其标准差分别为96.45±0.13和95.40±0.35；在其他性能指标方面几乎可以观察到类似的结果。结果表明，增强方案1比方案2具有更好的性能。在此基础上，本文的其他实验均采用方案1。

其次，根据总体结果可以看出，金字塔模型(M5到M8)的结果优于或等于两种增强方案的传统模型的结果。此外，在大多数情况下，金字塔模型M5给出了最好的结果，在完全连接的情况下，具有0.5个和20个神经元层；它与20个神经元一起工作比在完全连接的层中40个神经元更好。显然，M5是最好的模型，它的性能略高或相近，但涉及的参数最少；与参数较多的模型(M1、−、M4)相比，这种模型易于在内存有限的低成本芯片上部署。在所有后续实验中，我们使用具有增强方案1的模型M5。

5. Results

在模型选择后，即M5与增强方案1，我们提出并讨论了与癫痫检测相关的不同实验案例的结果。我们考虑了三个实验案例:(i)正常vs间歇期vs间歇期(AB vs CD vs E)， (ii)正常vs癫痫(AB vs CDE和AB vs CD)， (iii)癫痫发作vs非癫痫发作(A vs E, B vs E, A + B vs E, C vs E, D vs E, C + D vs E)。AB vs. CD vs. E, AB vs. E, A vs. E, B vs. E, CD vs. E, C vs. E, D vs. E, BCD vs. E, BC vs. E, BD vs. E, AC vs. E, ABCD vs. E, AB vs. CDE, ABC vs. E和ACD vs. E，在16个实验中，有14个被大多数研究频繁考虑，例如Sharmila和Geethanjali(2016)。剩下的两个实验很少或从未被测试过。所有实验均采用10倍交叉验证。

5.1. Experiment 1: normal vs ictal vs interictal classification (AB vs CD vs e) 

Zhang et al. (2017) 指出最近的几项研究工作对正常与癫痫发作或非癫痫发作脑电图信号的分类达到了近10%的准确性。然而，较少的工作投入到正常与间隔信号和间隔信号的分类。他们专门针对这三类问题提出了一个系统，取得了97.35%的准确率。

使用M5模型，单一P-1D-CNN模型的平均准确率为96.1%，3个P-1D-CNN模型的平均准确率为99.1%，比(Zhang等人，2017)高出1.7% (Bhattacharyya, Pachori, Upadhyay， & Acharya, 2017)高出0.5%。这一问题的详细性能分析如表3所示，其中显示了所有模型和增强方案的平均结果。然而，表4和表5显示了这个问题的10倍交叉验证结果和混淆矩阵。表5指出，主要混淆出现在nor- mal和inter-ictal或inter-ictal和ictal之间。

 

 

5.2. 实验2:正常vs癫痫分类(AB vs CDE和AB vs CD)

本案例涉及两类实验，涉及二元分类问题:(i)正常(AB) vs非发作性癫痫(CD)， (ii)正常(AB) vs非发作性癫痫和发作性癫痫(CDE);10次交叉验证结果如表6所示。

 

在单一P-1D-CNN模型下，该系统对AB vs CD的平均准确率为98.2%，而在3个P-1D-CNN模型的集成下，该系统的平均准确率为99.8%。同样，平均敏感性和特异性分别为98%和99%。在AB vs CDE的情况下，单模型和集成的平均准确性分别为98.1%和99.95%，而平均敏感性和特异性均为98%。结果表明，该系统具有更好的泛化性，优于Sharma、Pachori和Acharya(2017)和Sharmila和Geethan- jali(2016)中报道的最新方法。同时指出P-1D-CNN模型的综合效果优于单一的P-1D-CNN模型，这是因为在综合过程中，每个模型都是一个专家，对信号的局部部分进行分析，最后通过多数投票将局部决策进行融合，得出最终决策。

5.3. 实验3:正常或非发作vs发作分类(A vs E, B vs E, A + B vs E, C vs E, D vs E, C + D vs E)

第三组实验涉及6个二类问题(i)正常(A) vs发作(E)， (ii)正常(B) vs发作(E)， (iii)正常(AB) vs发作(E)， (iv)非发作(C) vs发作(E)， (v)非发作(D) vs发作(E)， (vi)非发作(CD) vs发作(E))。

我们测试了所有这些组合，以检查所提出的系统的鲁棒性。表7报告了结果。单一P-1D-CNN模型给出的平均值在99.9% ~ 97.4之间，而集成模型给出的平均值在10% ~ 98.5%之间。对于所有正常与癫痫发作的问题，综合诊断的准确性几乎为10%。对于C vs E问题，单一P-1D-CNN模型的平均准确率为98.1%，整体P-1D-CNN模型的平均准确率为98.5%;在这种情况下，集成有一点改进，这表明在这种情况下，几乎所有的专家(P-1D-CNN模型)有相同的决定，它不会产生重大影响。对于另外两个非癫痫发作与癫痫发作的问题，平均准确率分别为99.3%和99.7%，这表明这些问题比C对E相对容易。

6. Discussion

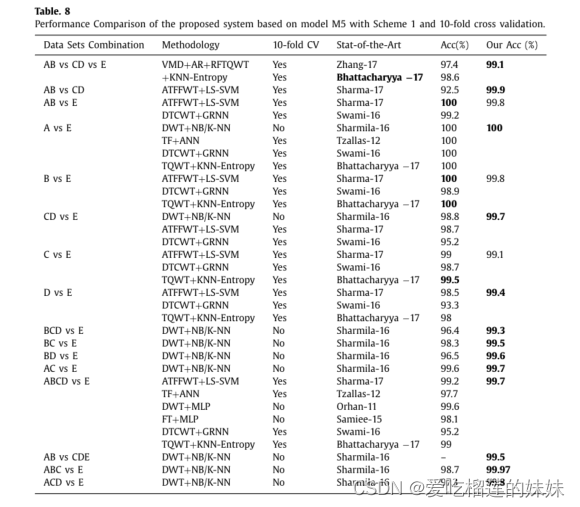
对于二元(正常与癫痫、发作与非发作)和三元(正常与发作间歇期与发作期)分类问题，已经提出了许多方法。表8给出了与最先进方法的比较：Zhang-17(Zhang等人，2017)、Bhattacharyya-17(Bhattacharyya等人，2017)、Sharma-17(Sharma等人，2017)、Swami-16(Swami等人，2016)、Sharmila-16(Sharmila&Geethan-jali，2016)、Samiee-15(Samiee等人，2015)、Orhan-1(Orhan等人，201 1)、Tzallas-12(Tzallas等人，2012)。据我们所知，到目前为止还没有使用动态链接法来解决这个问题。最近，Zhang等人提出了一种基于变分模式分解(VMD)的融合技术和基于自回归的二次特征提取技术。(2017)。使用随机森林分类器将提取的特征分为三类。尽管使用了多种复杂技术，但对于三类问题，它的准确率达到了97.35%，我们的系统达到了1.7%的高准确率，即99.1%。

Bhattacharyya等人提出的技术。(2017)使用可调Q小波变换(Tqwt)计算基于品质因子(Q)的多尺度熵度量，并将其用作特征。该方法的性能是基于Q和Tqwt的剩余参数(R)的调节。我们的方法在A与E，B与E，C与E，D与E，ABCD与E，AB与CD与E上进行了测试。我们的方法在D与E，ABCD与E，AB与CD与E上的性能优于它。然而，在B与E和C与E的两种情况下，它给出了更好的结果，但差异不显著，参见表8。这种方法的缺点是需要手动调整参数，并且依赖于数据。

Sharmila和Geethanjali(2016)提出的方法采用离散小波变换(DWT)进行特征提取，朴素贝叶斯(NB)和k近邻(k-NN)用于癫痫和非癫痫信号的分类。该方法报道的结果没有10倍交叉验证。表8显示，用10倍交叉验证评估的拟议系统总体上优于执行最好的方法(Sharmila&Geethanjali，2016；Bhattacharyya等人，2017)。有趣的是，观察到Sharmila和Geethanjali(2016)和Bhattacharyya等人的方法。(2017)不一致，即它们在不同情况下的表现存在显著差异。这表明，这些系统不能很好地适用于不同的情况，并依赖于数据。另一方面，该系统在所有情况下都表现出一致的性能，即对于不同的情况，准确率从99.1%到99.97%不等，略有差异是由于问题的性质；这意味着它不太依赖数据，具有较好的鲁棒性和比最新方法更好的泛化能力。对于所有16种情况(如上列的表8所示)，所提出的系统的平均准确率为99.6%，这验证了所提出的系统的泛化能力。

现有的所有系统都是基于人工设计的特征提取技术，需要对参数进行调整，其性能在很大程度上依赖于超参数和数据的选择，没有学习数据的内部结构。因此，它们不能很好地在不同的数据集上进行泛化，即不同的案子。此外，它们还涉及费力的设计，即首先提取和选择特征，然后将其传递给分类器，所有这些阶段都涉及到超参数，其联合调整是费力的。相反，该系统是一个端到端的系统，它基于深度学习理论，接受输入信号并给出决策，不需要任何信号预处理、人工特征提取和选择以及局部参数调整。它从数据中自动学习判别信息，学习过程完全自动化。与基于手工设计技术的传统系统相比，拟议系统的唯一缺点是必须始终保留学习的模型。值得注意的是，与其他CNN模型相比，我们的设计需要最小的存储空间。基于金字塔设计的P-1D-CNN模型(M5、M6、M7)与三类情况下的类似标准CNN模型相比，参数个数最少。最好的基于金字塔的P-1D-CNN模型(M5)包含8347个参数，是类似标准CNN模型(M1)包含的21,387个参数的39%，即M5包含的参数至少少61%。较少的参数不仅确保了更好的泛化，而且还导致了较少的存储开销。

我们在一台笔记本电脑上训练了P-1D-CNN模型，该笔记本电脑配备了英特尔酷睿i7-6700HQ CPU@2.60 GHz，具有16 GB RAM，4 GB Nvidia GeForce GTX 965 M显卡。对于P-1D-CNN模型的训练，我们使用了22,400个EEG信号，每个EEG信号由512个样本组成；一个历元(训练和验证)花费了4.33秒。在测试场景中，系统接受1024个样本的EEG信号作为输入并预测其类别。在AB、CD和E三种情况下，一个实例的预测时间在有GPU加速的情况下为0.0 0 0 142s，而在没有GPU加速的情况下为0.0 0 481s，这表明所提出的系统适合于部署在小型FG-PAS中；在这种情况下，系统的唯一弱点可能是内存和存储需求。由于高精度和实时性能，该系统可以部署在临床环境中，以帮助神经科学家。

7. Conclusion 

本文提出了一种癫痫自动检测系统，它处理二元检测问题(癫痫与非癫痫或发作与非癫痫)和三元检测问题(发作期与正常发作与发作间歇期)。该系统被设计为一种记忆效率高且简单的一维深卷积神经网络(P-1D-CNN)模型的集成，它以脑电信号为输入，将其传递给不同的基本P-1D-CNN模型，最后利用多数投票来融合它们的决策。为了克服数据集小的问题，提出了两种数据增强方案。由于该模型具有较少的参数和扩充方案，因此在有限数据的情况下易于训练，并且易于在内存有限的芯片上部署。它将帮助神经科医生发现癫痫，并将大大减轻他们的负担，提高他们的效率。

与拟议的工作相关的未来方向有很多。

虽然提出的系统在基准数据集上表现良好，但其临床验证和检查其在临床环境中部署的适宜性仍是未来的工作。另一个可能的方向是将其整合到癫痫患者的可穿戴设备中。尽管P-1D-CNN占用的内存和存储空间减少了约61%，但它对可穿戴设备的存储和内存要求可能是个问题。这个问题还需要进一步研究，以进一步降低内存和存储需求。此外，该系统可以部署在集中的云环境中，通过移动设备快速访问，而不使用特定的可穿戴设备。需要输入的小尺寸脑电信号和轻便的P-1D-CNN模型使其适合云部署。小信号可以很容易地传输到云中进行实时处理，在那里它可以生成警告警报，以便在必要时提醒医生/患者。在这方面，隐私保护和数据丢失是将数据传输到云中的一项艰巨任务。这些问题将在今后的工作中予以强调。该系统具有一定的通用性，可用于类似脑电信号疾病的专家系统开发，如工作指令应力检测。此外，通过增加模型的深度，增强基于CNN模型的多样性，可以对深层模型进行扩展，以设计出更具通用性和更强大的模型。