经典文献阅读之--lris（优于Scan Context的回环检测）_lidar iris for loop-closure detection

0. 前言

作为激光雷达的回环而言,最经典的仍然是Scan Context,但是Scan Context仍然会存在有一些缺陷，一是它只利用了最大的高度，丢失了很多点云信息，二是Scan-Context不具有旋转不变性，需要进行暴力匹配，三是Scan-Context缺少特征提取步骤。所以文章《LiDAR Iris for Loop-Closure Detection》,同时作者也将代码开源到了Github上:https://github.com/JoestarK/LiDAR-Iris,下面我们来详细梳理一下这篇文章.

1. 闭环策略

作为SLAM的回环来说,目前主要有四种闭环检测策略：

1. point-to-point matching，即点到点的匹配（如，ICP,NDT及其变种）；

2. 从3D点云中检测关键点，并从每个关键点位置中提取描述子，然后利用词袋模型（bag-of-words (BoW) model）进行场景匹配(BoW,BoW3d等)。

3. 从点云中提取以直方图的形式表示的全局描述子（如ESF, FPFH, VFH, M2DP,Scan Cntext）。

4. 基于卷积神经网络(CNNs)模型的方法。

2. 本文贡献

如上文所说,目前激光的全局或者局部的描述子能力和不变性有所欠缺,同时不具有旋转不变性,需要暴力的匹配,在Scan Context中使用了$N_r$ (Rings）的快速搜索算法来节省时间,但是也损失了对应的精度。而本文的方法解决了上述的缺陷

1. 提出了一个LiDAR点云的全局描述符LiDAR Iris，将一个地方总结为在LiDAR-Iris图像表示上进行几次Gabor过滤和阈值操作后获得的二进制签名图像, 充分利用了点云的大部分信息。
2. 该全局描述符具有旋转不变性，避免了暴力搜索，节约了计算资源。
3. 与现有的LIDAR全局描述符相比，该描述符的性能达到了SOTA。

3. 主要内容

准确的说,Lidar Iris描述符的生成理论上可以从执行上可以分解为三个模块:一是生成Lidar-Iris图像的表示；二是通过傅立叶变换使得Lidar-Iris具有平移不变性；三是基于LoG-Gabor滤波器的二值特征提取。下面我们就来对这三个执行模块进行分析.

3.1 LiDAR-lris图像

首先和Scan Context思想类似,即将三维点云映射成二维图像，对应的方法如下图所示

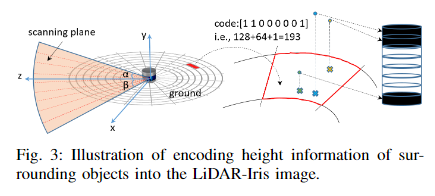
作者保留了一个以雷达为中心的$k\ast k(m)$的一个正方形作为有效感应区(本文取$k=80m$)，激光雷达的位置作为正方形的中心。以这个正方形为单位，将点云离散为80(沿半径的方向的) * 360(角向)的bin。值得注意的是，压缩成二维平面后，每一个区域中仍然具有高度、距离、反射率等特性，如果舍去就和栅格地图无异了，所以作者通过八位二进制代码对同一个bin内的所有点进行编码。以高度的编码方法举例，对于每一个bin内的点云集，首先按照高度的大小顺序，线性离散为8个bin，并不是每个bin都会有点，有点的bin值为1，否则为0，从而可以获得上图中的8位二进制编码。

同时借鉴了虹膜算法，将我们bin的环形鸟瞰图转化为像素条，形成和Scan Context类似的结果，有区别的是Lidar-IRIS图像的像素强度为每个bin的8位二进制数所转换的十进制数，而Scan Context是获取了当前位置的最高高度，这样其实是丢失了很多信息。

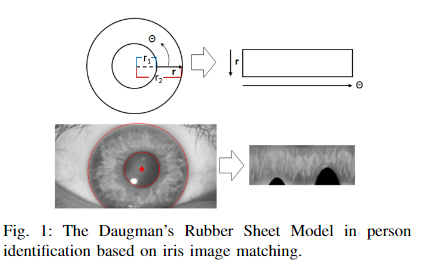
最后，与现有的基于直方图的全局描述符相比，所提出的编码过程不需要对每个bin中的点进行计数，从而提高了计算效率，但是又保存了大致的特征，不会受到噪声的干扰。

3.2 平移不变性Lidar-Iris的傅立叶变换

虽然在空间上来看是一个圆，应该有旋转不变性。但我们按照$0-2\pi$展开成 2D 图像后，像素条 对 Lidar 的朝向就变得敏感了。朝向稍微偏几度可能整体图像就有比较大的平移从而不相似了。所以作者提出了平移不变性Lidar-Iris的傅立叶变换。在学过图像处理的同学知道，傅里叶频谱可以有效地解决平移导致匹配重合度不高的问题

同时傅里叶本身又具有旋转变化性，这就导致非常适合我们的像素条的监测。

基于傅里叶变换的方案能够估计粗略的点云旋转、缩放和平移(用不到缩放)。点云的旋转对应于经过傅里叶变换后的Lidar-IRIS图像的水平平移，反映到傅里叶变换后两幅图像是完全没有差异的。

而点云的平移则是对应傅里叶变换后的 LiDAR-Iris 图像的垂直方向上的平移，会引起Lidar-IRIS 图像像素强度的轻微变化，从而导致傅里叶变换后本身的频谱发生轻微的变化。 但是Lidar-IRIS以bin为最小单位保留了点云的绝对内部结构，并没有那么高的分辨率，所以提高了辨别能力的同时又对图像像素强度的变化具有鲁棒性, 所以可以忽略由机器人在小范围内平移引起的 LiDAR-Iris 图像中强度的变化。

假设两个Lidar-IRIS图像仅仅差别一个位移(${\delta }_x,{\delta }_y$)，例如$I_1(x,y)=I_2(x-\delta x,y-\delta y)$,那么这两个图像之间的傅立叶变换可以定义为
$${\hat{I}}_1(w_x,w_y){\hat{e}}^{-i(w_x{\delta }_x+w_y{\delta }_y)}={\hat{I}}_2(w_x,w_y)$$

对应的，归一化的交叉功率谱定义为:
$$\widehat{Corr}=\frac{{\hat{I}}_2\left(w_x,w_y\right)}{{\hat{I}}_1\left(w_x,w_y\right)}==\frac{{\hat{I}}_2\left(w_x,w_y\right){\hat{I}}_1\left(w_x,w_y\right)\ast }{\left|{\hat{I}}_1\left(w_x,w_y\right){\hat{I}}_1\left(w_x,w_y\right)\ast \right|}=e^{-i\left(w_x{\delta }_x+w_y{\delta }_y\right)}$$

其中$\ast$表示复共轭。我们可以看到在简化后的归一化的交叉功率谱之间的关系，只有和初始位置以及移动来变化的。取傅里叶逆变换$Corr(x,y)=F^{-1}(\widehat{Corr})=\delta (x-{\delta }_x,y-{\delta }_y)$，这意味着$Corr(x,y)$仅在 ( δ x , δ y ) = a r g max ⁡ x , y { C o r r ( x , y ) } (δ_x,δ_y) =arg \max_{x,y}\{Corr(x,y)\} (δx​,δy​)=argmaxx,y​{Corr(x,y)}为非零。

3.3 基于LoG-Gabor滤波器的二值特征提取

…详情请参照古月居