算法－图的强连通分量，图的最小生成树_图最小生成树联通分量怎么求

作者：喵喵爱编程 | 2024-07-03 04:21:58

踩

图最小生成树联通分量怎么求

1.图的强连通分量
(1). 定义
图的强连通分量是图论中的一个重要概念，主要在有向图中进行讨论。具体来说，如果在一个有向图G中，任意两个顶点vi和vj（其中vi大于vj）之间都存在一条从vi到vj的有向路径，同时也存在一条从vj到vi的有向路径，那么这两个顶点就被称为强连通。如果有向图G的每两个顶点都强连通，那么G就被称为一个强连通图。

进一步地，有向图G的极大强连通子图被称为强连通分量。这里，“极大”意味着如果添加任何额外的顶点，子图将不再保持强连通的属性。因此，强连通分量实际上是原图中满足强连通条件的最大的子图。

强连通分量在实际应用中有着重要的价值。例如，在复杂网络分析中，强连通分量可以帮助我们识别出网络中紧密连接、相互依赖的节点群体，这对于理解网络的结构和功能至关重要。此外，强连通分量还可以用于简化图的复杂度，将原图分解为多个更小的强连通分量，从而方便后续的分析和处理。

在算法实现上，有多种方法可以用来寻找有向图中的强连通分量，如Kosaraju算法、Tarjan算法和Gabow算法等。这些算法通常基于深度优先搜索（DFS）的思想，通过遍历图中的节点和边来识别强连通分量。

(2). Kosaraju算法求解图的强连通分量
Kosaraju算法是一种求解有向图强连通分量（Strongly Connected Components, SCC）的算法。这个算法的基本思想是分两步进行深度优先搜索（DFS）。首先，对原图进行DFS，并记录每个节点的完成时间（即退出DFS的时间）。然后，根据完成时间的逆序（从大到小），对节点进行第二次DFS，每次DFS找到的就是一个强连通分量。
(3). 实例
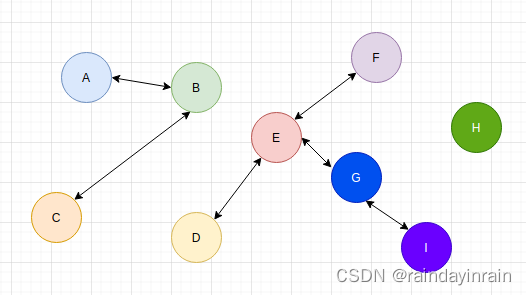
在这里插入图片描述
上述是一个图结构．利用Kosaraju算法可以求解其中每个强连通分量．

// 强连通分量
class NodeInfo{
public:
    char m_nName;
    bool m_bVisit = false;
    int32_t m_nTag = -1;
    int32_t m_nFirstTick;
    int32_t m_nLastTick;
};
template<class T>
class Node{
public:
    T m_nEle;
};
template<class EdgeInfo>
class Edge{
public:
    bool m_bValid = false;
};
Node<NodeInfo> stNodes[9];
Edge<int> stEdges[9][9];
Edge<int> stEdges2[9][9];
int nVisitTick = 0;
void Visit(int nCurIndex, int32_t nTag = -1);
 // 对节点按最后访问时间逆序排列
struct VisitInfo{
    int32_t nVisitTick;
    int32_t nIndex;
};
void Sort(VisitInfo* lpBegin, VisitInfo *lpEnd);
int main(){
    stNodes[0].m_nEle.m_nName = 'A';
    stNodes[1].m_nEle.m_nName = 'B';
    stNodes[2].m_nEle.m_nName = 'C';
    stNodes[3].m_nEle.m_nName = 'D';
    stNodes[4].m_nEle.m_nName = 'E';
    stNodes[5].m_nEle.m_nName = 'F';
    stNodes[6].m_nEle.m_nName = 'G';
    stNodes[7].m_nEle.m_nName = 'H';
    stNodes[8].m_nEle.m_nName = 'I';
    
    stEdges[0][1].m_bValid = true;
    stEdges[1][0].m_bValid = true;
    stEdges[1][2].m_bValid = true;
    stEdges[2][1].m_bValid = true;
    stEdges[4][5].m_bValid = true;
    stEdges[5][4].m_bValid = true;
    stEdges[4][3].m_bValid = true;
    stEdges[3][4].m_bValid = true;
    stEdges[4][6].m_bValid = true;
    stEdges[6][4].m_bValid = true;
    stEdges[6][8].m_bValid = true;
    stEdges[8][6].m_bValid = true;

    stEdges2[1][0].m_bValid = true;
    stEdges2[0][1].m_bValid = true;
    stEdges2[2][1].m_bValid = true;
    stEdges2[1][2].m_bValid = true;
    stEdges2[5][4].m_bValid = true;
    stEdges2[4][5].m_bValid = true;
    stEdges2[3][4].m_bValid = true;
    stEdges2[4][3].m_bValid = true;
    stEdges2[6][4].m_bValid = true;
    stEdges2[4][6].m_bValid = true;
    stEdges2[8][6].m_bValid = true;
    stEdges2[6][8].m_bValid = true;
    for(int i = 0; i < 9; i++){
        if(stNodes[i].m_nEle.m_bVisit == false){
            Visit(i);
        }
    }

    VisitInfo stArr[9];
    for(int32_t i = 0; i < 9; i++){
        stArr[i].nIndex = i;
        stArr[i].nVisitTick = stNodes[i].m_nEle.m_nLastTick;
    }
    // 按访问时间逆序排列数组元素
    Sort(stArr, stArr + 9);
    // 构造一个转置图，已经提前构建好．复用了原图的节点结构．深度优先前复位节点状态．
    for(int32_t i = 0; i < 9; i++){
        for(int32_t j = 0; j < 9; j++){
            stEdges[i][j] = stEdges2[i][j];
        }
    }
    for(int32_t i = 0; i < 9; i++){
        stNodes[i].m_nEle.m_bVisit = false;
        stNodes[i].m_nEle.m_nFirstTick = -1;
        stNodes[i].m_nEle.m_nLastTick = -1;
        stNodes[i].m_nEle.m_nTag = -1;
    }
    // 对转置图按排序后节点顺序再次执行深度搜索
    int32_t nTag = 0;
    for(int32_t i = 0; i < 9; i++){
        int32_t nNodeIndex = stArr[i].nIndex;
        if(stNodes[nNodeIndex].m_nEle.m_bVisit == false){
            Visit(nNodeIndex, nTag);
            nTag++;
        }
    }
    // 此时一次性求出了图的所有强连通分量．tag相同的节点位于同一个强连通分量．
    printf("strong connect num:%d\n", nTag);
    for(int32_t i = 0; i < nTag; i++){
        printf("%d:\n", i);
        for(int32_t k = 0; k < 9;  k++){
            if(stNodes[k].m_nEle.m_nTag == i){
                printf("%c ", stNodes[k].m_nEle.m_nName);
            }
        }
        printf("\n");
    }
    return 0;
}

void Sort(VisitInfo* lpBegin, VisitInfo *lpEnd){
    int32_t nNum = lpEnd - lpBegin;
    if(nNum <= 1){
        return;
    }

    // 归并排序
    int32_t nMid = nNum / 2;
    Sort(lpBegin, lpBegin+nMid);
    Sort(lpBegin+nMid,lpEnd);
   
    // 归并
    VisitInfo* lpArrTmp = (VisitInfo*)malloc(sizeof(VisitInfo) * nNum);
    int32_t nArrIndex = 0;
    int32_t nLeftIndex = 0;
    int32_t nRightIndex = 0;
    while(nLeftIndex < nMid && nRightIndex < (nNum - nMid)){
        if(lpBegin[nLeftIndex].nVisitTick >= lpBegin[nRightIndex+nMid].nVisitTick){
            lpArrTmp[nArrIndex] = lpBegin[nLeftIndex];
            nArrIndex++;
            nLeftIndex++;
        }
        else{
            lpArrTmp[nArrIndex] = lpBegin[nRightIndex+nMid];
            nArrIndex++;
            nRightIndex++;
        }
    }
    if(nLeftIndex < nMid){
        for(int32_t i = nLeftIndex; i < nMid; i++){
            lpArrTmp[nArrIndex] = lpBegin[i];
            nArrIndex++;
        }
    }
    else{
        for(int32_t i = nRightIndex; i < (nNum - nMid); i++){
            lpArrTmp[nArrIndex] = lpBegin[i+nMid];
            nArrIndex++;
        }
    }
    // 设置回去
    for(int32_t i = 0; i < nNum; i++){
        lpBegin[i] = lpArrTmp[i];
    }
}
// 基础的深度优先重点在于节点遍历．而不是，走完所有可能路径．
void Visit(int nCurIndex, int32_t nTag){
    nVisitTick++;
    stNodes[nCurIndex].m_nEle.m_bVisit = true;
    stNodes[nCurIndex].m_nEle.m_nFirstTick = nVisitTick;
    stNodes[nCurIndex].m_nEle.m_nTag = nTag;
    for(int i = 0; i < 9; i++){
        if(stEdges[nCurIndex][i].m_bValid && stNodes[i].m_nEle.m_bVisit == false){
            Visit(i, nTag);
        }
    }
    stNodes[nCurIndex].m_nEle.m_nLastTick = nVisitTick;
    nVisitTick++;// 用来保证LastTick不出现重复
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173

特意说明下，这里的深度优先访问是最基础的深度优先版本．此版本主要侧重于对每个可达节点执行一次访问．

2.图的最小生成树
(1). 定义
图的最小生成树（Minimum Spanning Tree，MST）是一个在图论中常见的概念。给定一个加权连通图（即图的每条边都有一个权重，连通图是图中任意两点均可相互到达的意思），最小生成树是一个子图，它包含了原图中的所有顶点，且所有的边都属于原图的边，同时边的权值和在所有这样的子图中是最小的。换句话说，最小生成树是一个连通所有顶点的树，且所有边的权值和最小。（也可说成是代价最小的连通所有顶点的子图）

最小生成树问题是一个优化问题，它在网络设计、电路设计等领域有广泛的应用。例如，在构建通信网络时，我们可能希望以最小的成本连接所有的城市，这就可以通过求解最小生成树问题来实现。

求解最小生成树问题的常见算法有两种：普里姆算法（Prim's algorithm）和克鲁斯卡尔算法（Kruskal's algorithm）。

普里姆算法：
图需要是无向图
(1). 将源节点加入当前最小生成树．
(2). 对所有边按权重排序．
(3). 循环迭代：
a. 从所有边中选出跨越当前最小生成树，图剩余部分的权重最小的边．跨越意味着此边一个节点在当前最小生成树中，另一节点不在．
b. 将此边的另一节点也加入当前最小生成树．
(4). 树中所有节点均加入最小生成树后，迭代结束．获得最小生成树．

克鲁斯卡尔算法：
(1).对图中的所有边按照权值大小进行排序．
(2). 按照权值从小到大的顺序依次选择边。
在选择每一条边时，需要判断这条边的两个顶点是否已经在同一个连通分量中，如果是，则跳过这条边；如果不是，则将这条边加入最小生成树中，并更新连通分量的信息。

(2). 实例
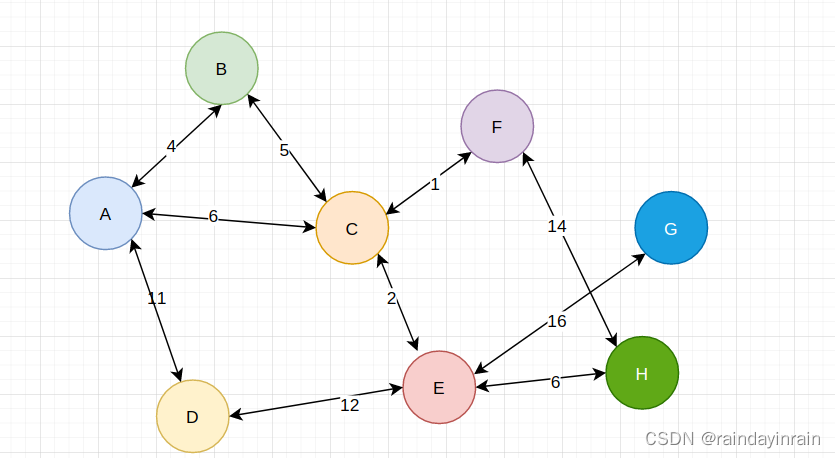
在这里插入图片描述

可利用上述算法求解上图中的一颗最小生成树．

声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】

算法－图的强连通分量，图的最小生成树_图 最小生成树 联通分量怎么求

算法－图的强连通分量，图的最小生成树_图最小生成树联通分量怎么求