循环队列的实现（附完整代码）

题目解读

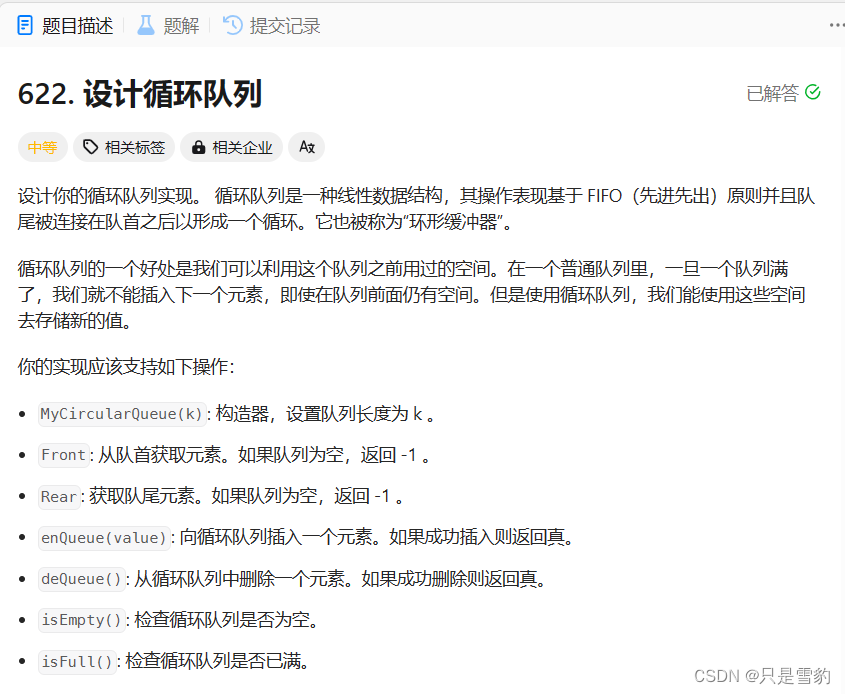
本题是要求我们设计一个循环的队列，循环队列要有以下功能：
1.获取队首元素，若队列为空返回-1
2.获取队尾元素，若队列为空，则返回-1
3.插入元素，插入成功返回真
4.删除元素，删除成功返回真
5.检查队列是否为空
6.检查队列是否已满
首先我们可以将之前写的用链表实现的队列的代码拷贝到该题中，以便于循环队列的实现，然后开始构思。
循环队列的解释题目中也给出了解释：
循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

解题构思

所以我们可以把循环队列先画图，他是一个环形的队列，并且首位相连尾接

那么，循环队列什么时候是满的，什么时候是空的呢？
其实，当队首和队尾在同一个位置时，这个时候队列就是空的，而当对头front的位置等于对尾rear的位置加1时，这个时候队列就是满的：

经过前面的构思，这个题目就很好理解了
但是还有一个问题很值得思考：
题目中对于循环队列的定义还有一个点很重要：
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。
什么意思呢？

也就是说，循环队列中我们如果在栈满了之后还想存储值，也是可以的，但是就要反复地使用之前用过的空间，会将其覆盖，所以尾指针rear和头指针front的位置的下标是会有覆盖的变化的

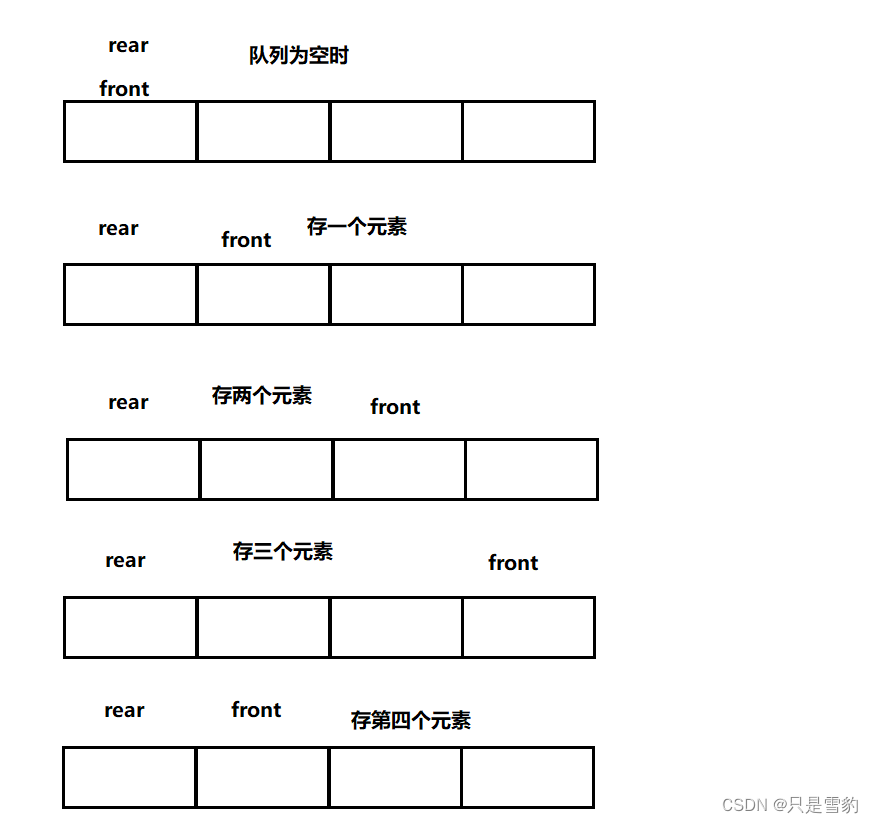
我们将循环队列形象地转换成数组：

这样你就能理解我上面所说的问题了！
你可以看到，队列为空时，按照题目的意思，front的位置时为rear+1的，在上图中，其实front的位置是0，rear的位置是3。
他们之间的关系就需要我们来求证一下了，因为在循环队列这个环形队列中，无论插入还是删除，都是从队头（或者是队尾）进行操作的！
我们其实就可以发现front的位置是与队列最大存储元素有关联的，上图中最大存储个数是3，当front存入4个元素时，存完第3个就满了，这个时候就应该重新从front位置开始存储，所以front（rear）和存储个数k有着以下关系：

就是说无论front的位置怎么移动，他最终都是在1-k的范围之内的

front  =  front  %  （ k + 1 ）
1

现在，我们就可以开始用代码实现循环队列：

循环队列的构造

我们首先定义一个结构体，就是循环队列的结构
首先就是front和rear分别为队首和队尾的下标位置
然后就是k，存储元素个数
还有数组a，存储元素

typedef struct 
{
    int front;
    int rear;
    int k;
    int* a;
} MyCircularQueue;
1
2
3
4
5
6
7

然后我们就可以构造一个循环队列了

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->rear=0;
    obj->k=k;
    return obj;
}
1
2
3
4
5
6
7
8

判断循环队列是否为空

我们在前面的解题构思中就知道，当front和rear相等时，循环队列就为空了，所以我们直接返回obj->front==obj->rear，如果队列为空，就返回 1，队列不为空就返回0

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front==obj->rear;
}
1
2
3
4

判断循环队列是否已满

当rear+1和front相等时就是满的
这里能这样写吗？答案是不能，他要除以k+1然后取余，和front的方法一样

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->rear+1)%(obj->k+1)==obj->front;
}
1
2
3
4

循环队列插入元素

如果队列已经满了我们就直接返回false即可
如果不是满的话就要将数组rear位置下标的值赋值为你要插入的元素的值
同时rear++，然后取余，最后返回true

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->rear]=value;
    obj->rear++;
    obj->rear %= (obj->k+1);
    return true;
}
1
2
3
4
5
6
7
8
9
10
11

循环队列删除元素

当队列为空时就不能删了，返回-1
不为空时，我们就将front的位置往前移动，这样队首的元素就被删除了
同时记得取余

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front %= (obj->k+1);   
    return true;
}
1
2
3
4
5
6
7
8
9
10

获取循环队列队首元素

这个也很简单，直接返回数组的front下标位置的元素即可

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[obj->front];
}
1
2
3
4
5
6
7
8

获取循环队列尾首元素

返回队尾元素我们就要根据图来具体求下标的关系了
由于画图较为麻烦，作者水平很有限，故不画图，给上源码，诸位大佬自己琢磨

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}
1
2
3
4
5
6
7
8

循环队列的销毁

free循环队列目标的同时记得把数组也给free掉，不然可能会出现内存泄漏

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}
1
2
3
4
5

完整代码如下：

typedef struct 
{
    int front;
    int rear;
    int k;
    int* a;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->rear=0;
    obj->k=k;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->rear]=value;
    obj->rear++;
    obj->rear %= (obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front %= (obj->k+1);   
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

好了，今天的分享到这里就结束了，谢谢大家的支持！