【机器学习】期望最大化（EM）算法_期望最大化算法

EM是一种解决 存在隐含变量优化问题 的有效方法。EM的意思是“期望最大化（Expectation Maximization）” 。EM是解决（不完全数据，含有隐变量）最大似然估计（MLE）问题的迭代算法 。

EM算法有很多的应用，最广泛的就是混合高斯模型GMM、隐马尔可夫模型HMM、贝叶斯网络模型等等。

在介绍具体的EM算法前，我们先介绍 极大似然估计 和 Jensen不等式。

一、极大似然估计

极大似然估计法是一种求估计的统计方法，它建立在极大似然原理的基础之上。

1.1 基本原理

极大似然估计的原理是：一个随机试验如有若干个可能的结果A，B，C，…。若在一次试验中，结果A出现，则一般认为试验条件对A出现有利，也即A出现的概率很大。极大似然估计就是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。 这也是统计学中用样本估计整体的一种阐述。

1.2 举例说明

【任务】：估计某个学校的男生的身高分布。 假设你在校园里随便找了100个男生，他们的身高是服从高斯分布的。但是这个分布的均值u和方差σ我们不知道，记作$\theta =[u,\sigma ]$。
　　
【问题】：我们知道样本所服从的概率分布的模型和一些样本，而不知道该模型中的参数？

【如何估计】：

• 样本集$X=x_1,x_2,\dots ,x_N$，其中 N=100
• 概率密度：$p(x_i|\theta )$ 为抽到男生i（的身高）的概率。 100个样本之间独立同分布，所以我同时抽到这100个男生的概率就是他们各自概率的乘积。就是从分布是 $p(x|\theta )$ 的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：
  

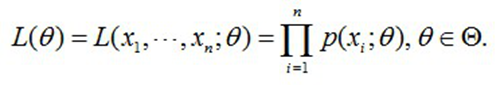
上式反映了在概率密度函数的参数是θ时，得到X这组样本的概率。

需要找到一个参数θ，其对应的似然函数L(θ)最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做θ的最大似然估计量，记为：

【求解步骤】：

1. 首先，写出似然函数：
   
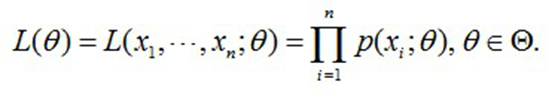
2. 然后，对似然函数取对数：
   
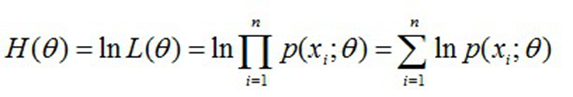
3. 求导数，令导数为0，得到似然方程；
4. 最后，解似然方程，得到的参数即为所求。

【总结】：
极大似然法：知道样本所服从的概率分布模型，而不知道该模型中的参数，需要求参数。

具体步骤如下：

1. 已知概率模型，根据概率密度函数写出联合概率（似然函数）；
2. 对似然函数取对数；
3. 求导。令导数等于0，求出参数。

注意：这里是通过求导来实现求解。若是求导不好解，可以在似然函数前面乘以负值，改写成最小化目标函数，然后用梯度下降法求解。具体可以参考logistic regression的求解方法。

多数情况下我们是根据已知条件来推算结果，而极大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

二、Jensen不等式

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。
Jensen不等式表述如下：如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])。当且仅当X是常量时，上式取等号。

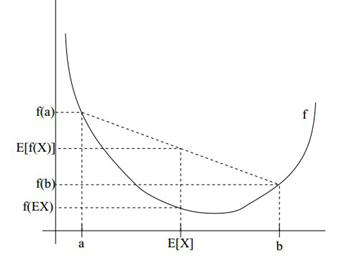
三、EM算法

【任务】：估计某个学校的男生和女生的身高分布。 我们抽取了100个男生和100个女生样本的身高，但是我们不知道每一个人到底是从男生还是女生的身高分布中抽取的。

用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。 这个时候，对于每一个样本，就有两个东西需要猜测或者估计：
(1)这个人是男的还是女的？
(2)男生和女生对应的身高的高斯分布的参数？

EM算法要解决的问题是：
(1)求出每一个样本属于哪个分布
(2)求出每一个分布对应的参数

如果把这个数据集的概率密度画出来，大约是这个样子：

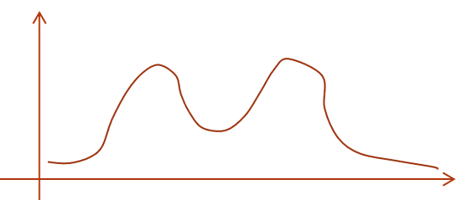
　其实这个双峰的概率密度函数是有模型的，称作混合高斯模型（GMM）。GMM其实就是k个高斯模型加权组成，α是各高斯分布的权重，Θ是参数。

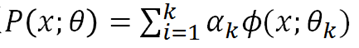
　对GMM模型的参数估计，就要用EM算法。更一般的讲，EM算法适用于带有隐变量的概率模型的估计。

3.1 隐变量 与 观测变量

首先给出观测变量与隐变量的定义：

• 观测变量: 模型中可以直接观测，即在研究中能够收集到的变量成为观测变量。
• 隐变量: 模型中不可观测的随机变量，我们通常通过可观测变量的样本对隐变量作出推断。

在上述例子中，隐变量就是对每一个身高而言，它属于男生还是女生。

3.2 为什么要用EM

我们来具体考虑一下上面这个问题。如果使用极大似然估计（这是我们最开始最单纯的想法），那么我们需要极大化的似然函数应该是这个：

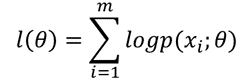
然而我们并不知道p(x;θ)的表达式。这里考虑隐变量，如果我们已经知道哪些样本来自男生，哪些样本来自女生。用Z=0或Z=1标记样本来自哪个总体，则Z就是隐变量，需要最大化的似然函数就变为：

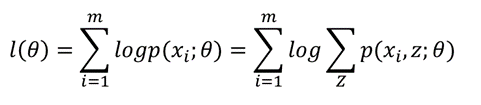
然而我们并不知道隐变量的取值。要估计一个样本是属于男生还是女生，我们就要有模型参数，要估计模型参数，我们首先要知道一个样本属于男生还是女生的可能性。（鸡生蛋，蛋生鸡）

这里，我们利用假设来求解：

• 首先假设一个模型参数θ，然后每个样本属于男生还是女生的概率p(zi)就能算出来了，p(xi,zi)=p(xi|zi)p(zi)。而x|z=0服从女生身高分布，x|z=1服从男生身高分布，所以似然函数可以写成含有θ的函数，极大化它我们可以得到一个新的θ。
• 新的θ因为考虑了样本来自哪个分布，会比原来的更能反应数据规律。有了这个更好的θ我们再对每个样本重新计算它属于男生还是女生的概率，用更好的θ算出来的概率会更准确。
• 有了更准确的信息，我们可以继续像上面一样估计θ，自然而然这次得到的θ会比上一次更棒，如此直到收敛（参数变动不明显了）。

实际上，EM算法就是这么做的。

事实上，隐变量估计问题也可以通过梯度下降等优化算法求解，但由于求和的项数将随着隐变量的数目以指数级上升，会给梯度计算带来麻烦。而EM算法则可以看作是一种非梯度优化方法。

3.3 引入Jensen不等式

然而事情并没有这么简单，上面的思想理论上可行，实践起来不成。主要是因为似然函数有“和的log”这一项，log里面是一个和的形式，求导复杂。直接强来你要面对 “两个正态分布的概率密度函数相加”做分母，“两个正态分布分别求导再相加”做分子的分数形式。m个这玩意加起来令它等于0，要求出关于θ的解析解，你对自己的数学水平想的不要太高。此处，考虑到Jensen不等式，有
直接最大化似然函数做不到，那么如果我们能找到似然函数的一个紧的下界一直优化它，并保证每次迭代能够使总的似然函数一直增大，其实也是一样的。（利用紧下界迭代逼近）

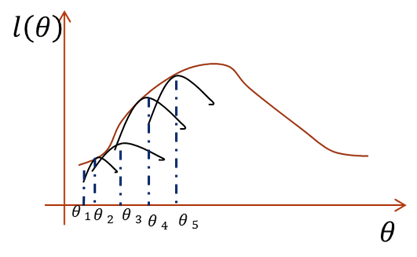
横坐标是参数，纵坐标是似然函数，首先我们初始化一个θ1，根据它求似然函数一个紧的下界，也就是图中第一条黑短线。黑短线上的值虽然都小于似然函数的值，但至少有一点可以满足等号（所以称为紧下界），最大化小黑短线我们就hit到至少与似然函数刚好相等的位置，对应的横坐标就是我们的新的θ2。如此进行，只要保证随着θ的更新，每次最大化的小黑短线值都比上次的更大，那么算法收敛，最后就能最大化到似然函数的极大值处。

构造这个小黑短线，就要靠Jensen不等式。注意我们这里的log函数是个凹函数，所以我们使用的Jensen不等式的凹函数版本。根据Jensen函数，需要把log里面的东西写成数学期望的形式，注意到log里的和是关于隐变量Z的和。于是，这个数学期望一定是和Z有关，如果设Q(z)是Z的分布函数，那么可以这样构造：


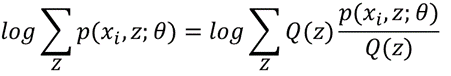
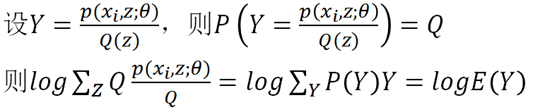
所以log里其实构造了一个随机变量Y，Y是Z的函数，Y取p/Q的值的概率是Q。构造好数学期望，下一步根据Jensen不等式进行放缩：

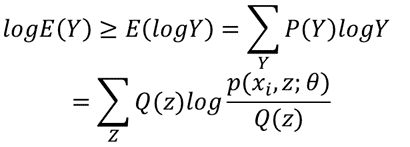
有了这一步，我们看一下整个式子：

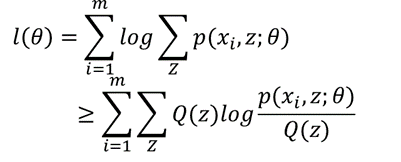
也就是说我们找到了似然函数的一个下界，那么优化它是否就可以呢？不是的，上面说了必须保证这个下界是紧的，也就是至少有点能使等号成立。由Jensen不等式，等式成立的条件是随机变量是常数，具体就是：

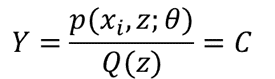
又因为Q(z)是z的分布函数，所以：
　　

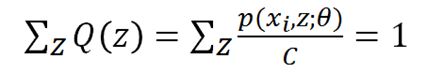
把C乘过去，可得C就是p(xi,z)对z求和，所以我们终于知道了：
　　

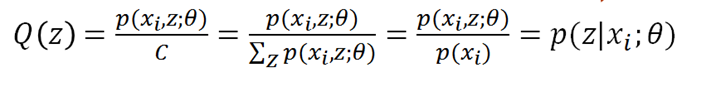
得到Q(z)，大功告成。Q(z)就是p(zi|xi)，或者写成p(zi)，代表第i个数据是来自zi的概率。

3.4 EM算法步骤

初始化分布参数θ，重复以下步骤直到收敛：

1. E-Step：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。 作为隐变量的现估计值。（根据参数θ计算每个样本属于zi的概率，即这个身高来自男生或女生的概率）

2. M-Step：将似然函数最大化以获得新的参数值。 根据计算得到的Q，求出含有θ的似然函数的下界并最大化它，得到新的参数θ。

3.5 EM算法总结

• EM算法是一种从不完全数据或有数据丢失的数据集（存在隐变量）中求解概率模型参数的最大似然估计方法。
  • 第一步求隐变量的期望(E)
  • 第二步求似然函数极大(M)
• EM算法在一般情况是收敛的，但是不保证收敛到全局最优，即有可能进入局部的最优。
• 应用到的地方：混合高斯模型GMM、隐马尔科夫模型HMM、贝叶斯网络模型等。

参考资料

• 【机器学习】EM算法详细推导和讲解