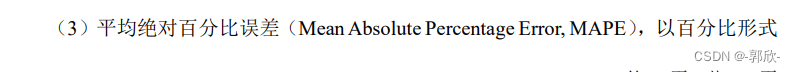机器学习辅助的乙醇浓度检测（毕设节选）

目录

1.为什么要机器学习

2. 神经网络一般组成

3.BP神经网络工作过程

 4.评价指标

5.实操代码

1.为什么要用机器学习

人工分析大量的谐振模式，建立各种WGM的响应与未知目标之间的关系，是一个很大的挑战。机器学习(ML)能够自行识别全谱的全部特征。作为一种数据驱动的分析技术，它可以自动从大型数据集中搜索有效信息，揭示数据背后的机制，从而建立数据之间的映射关系输入数据与未知目标参数。（我的理解是，采集的是乙醇的光谱数据，人眼识别或者记录比较困难，故而借助机器学习。）

2. 神经网络一般组成

（1）输入层：输入层是神经网络的起始部分，它的作用是接收外部输入的数据。输入层的设计直接影响到神经网络的性能，因为它决定了网络能够接收和处理的信息类型和结构。

（2）隐藏层：隐藏层在神经网络中的作用尤为重要，它们负责特征的转换和提取。通过应用非线性变换，隐藏层能够提升模型对复杂数据的表达能力。

（3）输出层：输出层是模型的最后一层，它的任务是生成模型的最终预测结果。这一层的神经元数量与所解决的问题类型密切相关。在回归问题中，通常只需要一个输出神经元来预测连续的数值；而在分类问题中，输出神经元的数量则与目标类别的数量一致。

（4）权重和偏置：这些是网络中的参数，可以在训练过程中进行学习。权重决定了输入特征如何影响隐藏层和输出层，而偏置则用于调整神经元的激活水平。

（5）激活函数：激活函数是神经网络中的关键组件，它负责为网络引入非线性。在神经网络中，每个神经元在接收到输入信号后，会通过一个激活函数来决定是否以及如何激活。

（6）损失函数：损失函数（Loss Function）是神经网络训练过程中用于衡量模型预测值与实际值之间差异的函数。它为网络提供了一个优化的目标，即最小化损失函数的值。损失函数的选择取决于具体的任务和模型的需求。

（7）优化器：优化器在神经网络训练中起着至关重要的作用，它的主要工作是调整网络的权重和偏置，目的是减少损失函数的值。

3.BP神经网络工作过程

（1）初始化：首先，需要初始化网络中的权重和偏置。

（2）输入数据：将输入数据送入网络，进而传递到第一层的神经元，即输入层。

（3）前向传播：数据在网络中逐层向前传递，每一层的神经元接收来自前一层的输出，通过激活函数处理，生成当前层输出。激活函数常使用Sigmoid、Tanh或ReLU等。

（4）计算误差：在网络的最后一层，即输出层，计算预测结果与实际目标值之间的误差。误差通常使用均方误差（Mean Squared Error, MSE）或其他损失函数来衡量。

（5）反向传播：利用计算出的误差，通过反向传播算法调整网络中的权重和偏置。这个过程涉及到梯度的计算，即损失函数对权重的偏导数。

（6）权重更新：根据反向传播得到的梯度信息，使用梯度下降或其变体（如动量法、AdaGrad等）来更新权重和偏置。

（7）迭代训练：重复步骤（3）至（6），直到满足停止条件，如达到预定的迭代次数或误差降低到可接受的水平。

（8）评估和应用：训练完成后，使用测试数据集评估网络的性能，然后可以将训练好的神经网络应用于实际问题。

 4.评价指标

5.实操代码

%% BP神经网络回归预测
%% 1.初始化
clear all
close all
clc
format short %2位小数，format short精确4位，format long精确15位
 
%% 2.读取数据
data=xlsread("D:\Matlab\machine learning\machine learning.xlsx"); %使用xlsread函数读取EXCEL中对应范围的数据即可; xlsread函数报错时，可用Load函数替代 
 
% 设置神经网络的输入和输出
T=data(:,1);   %步长
X=data(:,2);   %第1列至倒数第2列为输入
Y=data(:,3);  %最后1列为输出
N=length(Y);  %计算样本数量
input=X;
output=Y;
 
%% 3.设置训练集和测试集
%（1）随机选取测试样本code5
k=rand(1,N);
[m,n]=sort(k);
testNum=9;              %设定测试集样本数量——修改
trainNum=N-testNum;       %设定训练集样本数量
input_train = input(n(1:trainNum),:)';                   % 训练集输入
output_train =output(n(1:trainNum))';                    % 训练集输出
input_test =input(n(trainNum+1:trainNum+testNum),:)';    % 测试集输入
output_test =output(n(trainNum+1:trainNum+testNum))';    % 测试集输出
 
%% 4.数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);         % 训练集输入归一化到[0,1]之间
%[outputn,outputps]=mapminmax(output_train,0,1);         
[outputn,outputps]=mapminmax(output_train);          % 训练集输出归一化到默认区间[-1, 1]
inputn_test=mapminmax('apply',input_test,inputps);   % 测试集输入采用和训练集输入相同的归一化方式
 
%% 5.求解最佳隐含层
inputnum=size(input,2);   %size用来求取矩阵的行数和列数，1代表行数，2代表列数
outputnum=size(output,2);
disp(['输入层节点数：',num2str(inputnum),',  输出层节点数：',num2str(outputnum)])
disp(['隐含层节点数范围为 ',num2str(fix(sqrt(inputnum+outputnum))+1),' 至 ',num2str(fix(sqrt(inputnum+outputnum))+10)])
disp(' ')
disp('最佳隐含层节点的确定...')
 
%根据hiddennum=sqrt(m+n)+a，m为输入层节点数，n为输出层节点数，a取值[1,10]之间的整数
MSE=1e+5;                             %误差初始化
transform_func={'tansig','purelin'};  %激活函数采用tan-sigmoid和purelin
train_func='trainlm';                 %训练算法
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10
    
    net=newff(inputn,outputn,hiddennum,transform_func,train_func); %构建BP网络
    
    % 设置网络参数
    net.trainParam.epochs=1000;       % 设置训练次数
    net.trainParam.lr=0.01;           % 设置学习速率
    net.trainParam.goal=0.000001;     % 设置训练目标最小误差
    
    % 进行网络训练
    net=train(net,inputn,outputn);
    an0=sim(net,inputn);     %仿真结果
    mse0=mse(outputn,an0);   %仿真的均方误差
    disp(['当隐含层节点数为',num2str(hiddennum),'时，训练集均方误差为：',num2str(mse0)])
    
    %不断更新最佳隐含层节点
    if mse0<MSE
        MSE=mse0;
        hiddennum_best=hiddennum;
    end
end
disp(['最佳隐含层节点数为：',num2str(hiddennum_best),'，均方误差为：',num2str(MSE)])
 
%% 6.构建最佳隐含层的BP神经网络
net=newff(inputn,outputn,hiddennum_best,transform_func,train_func);
 
% 网络参数
net.trainParam.epochs=1000;         % 训练次数
net.trainParam.lr=0.01;             % 学习速率
net.trainParam.goal=0.000001;       % 训练目标最小误差
 
%% 7.网络训练
net=train(net,inputn,outputn);      % train函数用于训练神经网络，调用蓝色仿真界面
 
%% 8.网络测试
an=sim(net,inputn_test);                     % 训练完成的模型进行仿真测试
test_simu=mapminmax('reverse',an,outputps);  % 测试结果反归一化
error=test_simu-output_test;                 % 测试值和真实值的误差
 
% 权值阈值
W1 = net.iw{1, 1};  %输入层到中间层的权值
B1 = net.b{1};      %中间各层神经元阈值
W2 = net.lw{2,1};   %中间层到输出层的权值
B2 = net.b{2};      %输出层各神经元阈值
 
%% 9.结果输出
% BP预测值和实际值的对比图
figure
plot(output_test,'bo-','linewidth',1.5)
hold on
plot(test_simu,'rs-','linewidth',1.5)
legend('实际值','预测值')
xlabel('测试样本'),ylabel('指标值')
title('BP预测值和实际值的对比')
set(gca,'fontsize',12)
 
% BP测试集的预测误差图
figure
plot(error,'bo-','linewidth',1.5)
xlabel('测试样本'),ylabel('预测误差')
title('BP神经网络测试集的预测误差')
set(gca,'fontsize',12)
 
 
%计算各项误差参数
[~,len]=size(output_test);            % len获取测试样本个数，数值等于testNum，用于求各指标平均值
SSE1=sum(error.^2);                   % 误差平方和
MAE1=sum(abs(error))/len;             % 平均绝对误差
MSE1=error*error'/len;                % 均方误差
RMSE1=MSE1^(1/2);                     % 均方根误差
MAPE1=mean(abs(error./output_test));  % 平均百分比误差
r=corrcoef(output_test,test_simu);    % corrcoef计算相关系数矩阵，包括自相关和互相关系数
R1=r(1,2);    
  
% 显示各指标结果
disp(' ')
disp('各项误差指标结果：')
disp(['误差平方和SSE：',num2str(SSE1)])
disp(['平均绝对误差MAE：',num2str(MAE1)])
disp(['均方误差MSE：',num2str(MSE1)])
disp(['均方根误差RMSE：',num2str(RMSE1)])
disp(['平均百分比误差MAPE：',num2str(MAPE1*100),'%'])
disp(['预测准确率为：',num2str(100-MAPE1*100),'%'])
disp(['相关系数R： ',num2str(R1)])
 
%%读取待预测数据
kes=xlsread("D:\Matlab\machine learning\self.xlsx");
 
%%数据转置
kes=kes';
 
%%数据归一化
n_test = mapminmax('apply',kes,inputps,0,1);
 
%%仿真测试
t_sim = sim(net,n_test);
 
%%数据反归一化
T_sim = mapminmax('reverse',t_sim,outputps,0,1);
 
%%保存结果
xlswrite('self_product',T_sim')