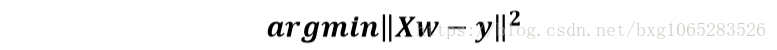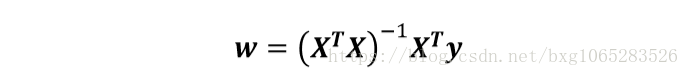9.机器学习sklearn-----岭回归及其应用实例_岭回归的应用场合

1.基本概念

对于一般地线性回归问题，参数的求解采用的是最小二乘法，其目标函数如下：

参数w的求解，也可以使用如下矩阵方法进行： 

      

对于矩阵X，若某些列线性相关性较大（即训练样本中某些属性线性相关），就会导致，就会导致XTX的值接近0，在计算(XTX)-1时就会出现不稳定性： 

结论：传统的基于最小二乘的线性回归法缺乏稳定性。

岭回归(ridge regression)是一种专用于共线性数据分析的有偏估计回归方法,是一种改良的最小二乘估计法，对某些数据的拟合要强于最小二乘法。

在sklearn库中，可以使用sklearn.linear_model.Ridge调用岭回归模型，其 主要参数有：

                     • alpha：正则化因子，对应于损失函数中的α

                     • fit_intercept：表示是否计算截距，

                     • solver：设置计算参数的方法，可选参数‘auto’、‘svd’、‘sag’等

2.实例

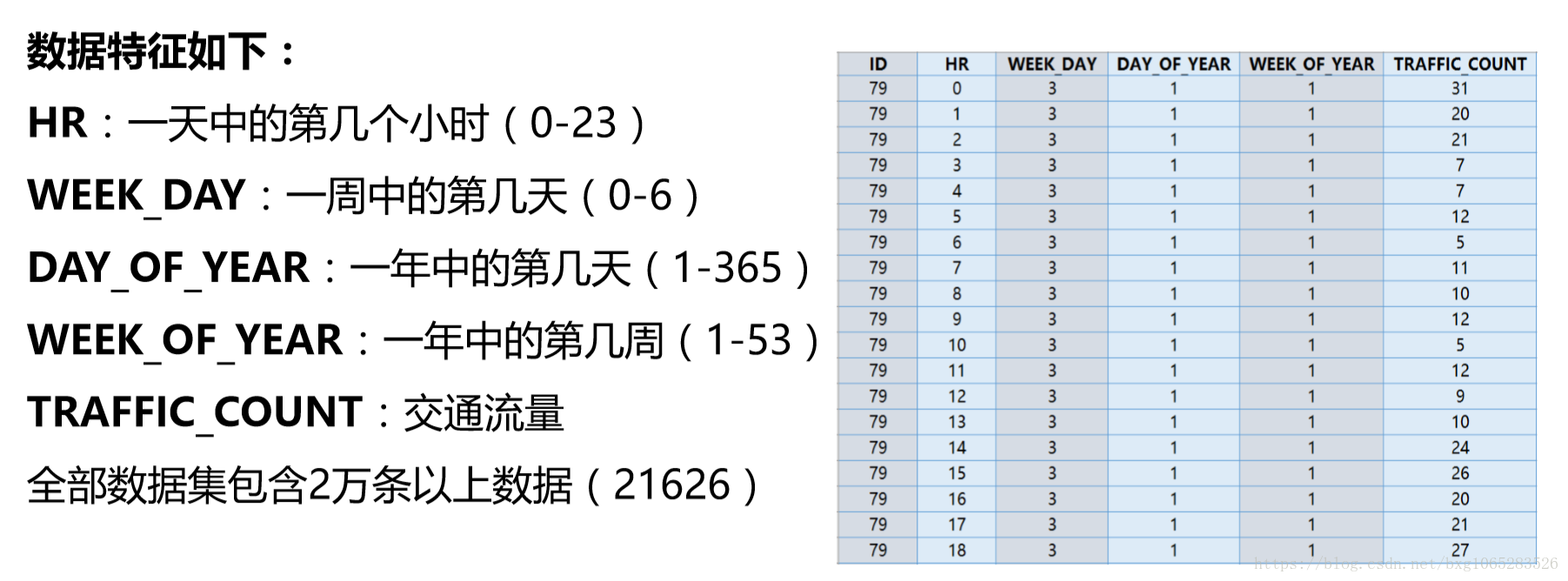
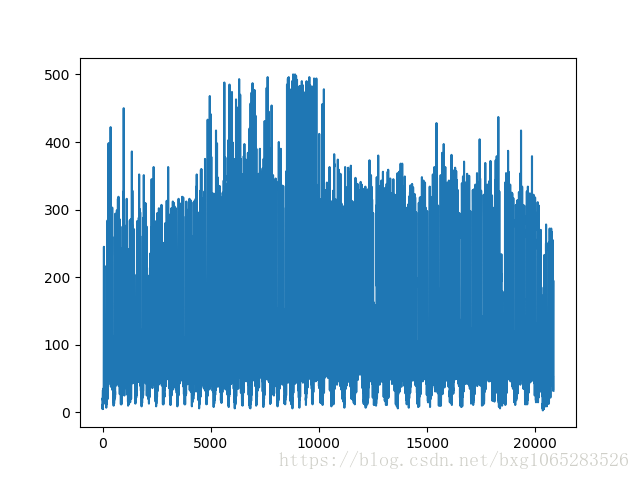
数据介绍： 数据为某路口的交通流量监测数据，记录全年小时级别的车流量。 

实验目的： 根据已有的数据创建多项式特征，使用岭回归模型代替一般的线性模型，对车流量的信息进行多项式回归。

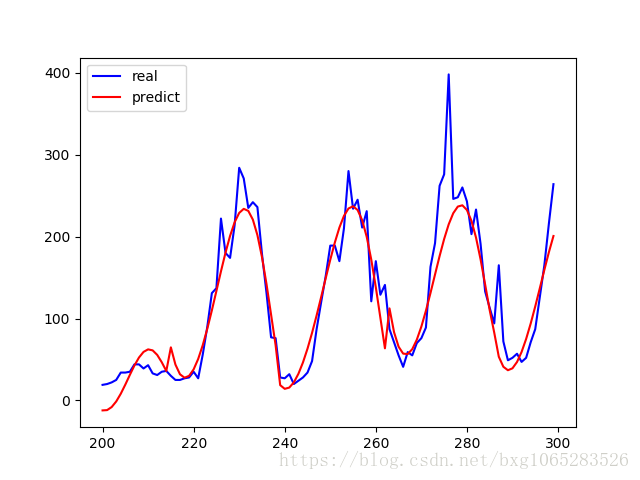
import numpy as np
import pandas as pd
#通过sklearn.linermodel加载岭回归方法
from sklearn.linear_model import Ridge
from sklearn import model_selection
#加载交叉验证模块
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
#使用numpy的方法从txt文件中加载数据
a=pd.read_csv('data.csv')
data=np.array(a)

#使用plt展示车流量信息
plt.plot(data[:,5])
plt.show()
#X用于保存0-5维数据，即属性
X=data[:,1:5]
#y用于保存第6维数据，即车流量
y=data[:,5]
#用于创建最高次数6次方的的多项式特征，多次试验后决定采用6次
poly =PolynomialFeatures(6)
#X为创建的多项式特征
X=poly.fit_transform(X)
#将所有数据划分为训练集和测试集，test_size表示测试集的比例，
#random_state是随机数种子
train_set_X,test_set_X,train_set_y,test_set_y=\
    model_selection.train_test_split(X,y,test_size=0.3,random_state=0)

#创建回归器，并进行训练
#创建岭回归实例
clf =Ridge(alpha=1.0,fit_intercept=True)
#调用fit函数使用训练集训练回归器
clf.fit(train_set_X,train_set_y)
#利用测试集计算回归曲线的拟合优度，clf.score返回值为0.7375拟合优度，
# 用于评价拟合好坏，最大为1，无最小值，
#当对所有输入都输 出同一个值时，拟合优度为0。
clf.score(test_set_X,test_set_y)

start =200 #花一段200到300范围内的拟合曲线
end =300
y_pre =clf.predict(X) #是调用predict函数的拟合值
time =np.arange(start,end)
plt.plot(time,y[start:end],'b',label="real")
plt.plot(time,y_pre[start:end],'r',label='predict')
plt.legend(loc='upper left')
plt.show()

结果：

分析结论：预测值和实际值的 走势大致相同