- 1大数据最全Spark与flink计算引擎工作原理(1),零基础学习大数据开发开发_spark引擎
- 2分布式系统技术系列--租约(lease) (转载)
- 32024年最全Python代码实现尼姆游戏聪明模式_尼姆游戏python代码,spring bean的生命周期面试题_编写程序模拟聪明版的尼姆
- 4C语言基础知识_c语言编程基础
- 5OWASP API Security Top 10解读
- 6使用Eclipse处理GIt冲突的一种方法_eclipse git rebase
- 7AndServer,一个Android端的web服务器_yanzhenjie:andserver:
- 8Linux信号处理机制原理_linux信号原理
- 9Echarts-vue_vue echarts 获取echarts对象
- 10【粉丝福利社】AI商业广告设计实战108招:ChatGPT+Photoshop+Firefly+Midjourney(文末送书-进行中)_midjourney广告设计
大模型思维链推理的综述:进展、前沿和未来_大模型推理链
赞
踩
前言
预训练语言模型(PLMs)能够自动从无标签文本中学习通用表示,并通过在下游任务上的微调实现出色的性能(Devlin等人,2019年;Raffel等人,2020年;Radford和Narasimhan,2018年)。最近,扩大语言模型的规模显著提高了性能,并带来了许多惊喜,例如突现能力(Wei等人,2022a;Schaeffer等人,2023年)。因此,自然语言处理的范式正从预训练加微调转变为预训练加上下文学习。然而,到目前为止,大规模语言模型(LLMs)在复杂推理任务上,如数学推理(Cobbe等人,2021年;Patel等人,2021年)、常识推理(Talmor等人,2021年;Mihaylov等人,2018年)等,仍有相当大的改进空间。
为了利用LLMs解决复杂推理任务,Wei等人(2022b)通过逐步推理过程扩展了上下文学习,首先引入了思维链(CoT)提示的概念。Kojima等人(2022年)发现,简单地在提示中添加一个魔法短语“让我们一步步来”就能使LLMs在没有任何人类注释的情况下执行零样本思维链推理。这些研究突出了思维链在增强模型复杂推理能力以及提高其推理和规划能力方面的重要性。
随后,关于X-of-thought(XoT)的大量工作像雨后的蘑菇一样在NLP社区迅速涌现,例如自动XoT构建(Kojima等人,2022年;Zhang等人,2023f;Xu等人,2023年),XoT结构变体(Chen等人,2022a;Ning等人,2023年;Lei等人,2023a;Yao等人,2023b)等。请注意,为了与原始的CoT区分开来,我们使用XoT来广泛地指代CoT,这是一个集体术语,用于指代逐步推理方法的使用。
然而,这些方法和数据集尚未经过系统性的回顾和分析。为了填补这一空白,我们提出这项工作来进行对XoT家族的全面和详细分析。尽管已经有一些综述讨论了思维链,但它们仅限于特定方面,例如使用提示的LLM推理(Qiao等人,2023年)和思维链提示策略(Yu等人,2023c)。相比之下,我们的综述不仅提供了对他们已经涵盖的主题的更全面和全面的讨论,还包括了额外的主题和讨论,如XoT构建、XoT结构变体和前沿应用等。具体来说,在本文中,我们首先介绍了相关背景和初步知识(第2节)。此外,我们从多个角度仔细分类了XoT系列工作,并完成了深入分析(第4节),包括XoT构建方法(4.1节)、XoT结构变体(4.2节)和XoT增强方法(4.3节)。然后,我们提供了XoT在前沿领域的实际应用(第5节)。为了激发XoT后续工作的灵感,我们提供了对这一领域未来研究潜在途径的见解(第6节)。最后,我们比较并讨论了现有的方法(第7节)。

2 背景和初步
2.1 背景
近年来,随着计算能力的不断扩展,大规模语言模型如雨后春笋般涌现(Brown等人,2020年;OpenAI,2023年;Touvron等人,2023a;Scao等人,2022年;Touvron等人,2023b;Zhao等人,2023b),随着模型规模的持续增长,许多新能力已经出现,例如上下文学习和思维链推理(Brown等人,2020年;Wei等人,2022b,a;Schaeffer等人,2023年)。
Brown等人(2020年)发现,大规模语言模型具有出色的上下文学习(ICL)能力。ICL将输入-输出演示融入到提示文本中。通过ICL,现成的LLMs可以在不进行额外微调的情况下使用,同时实现可比的性能。然而,这种端到端的方法在面对复杂推理任务时往往会表现不佳。
Wei等人(2022b)发现,通过在演示中添加逐步推理过程,可以提高LLMs的推理能力,这被称为思维链提示。CoT提示使模型能够更精确地理解问题的复杂性和推理过程。此外,模型生成了一系列推理步骤,这为我们提供了对模型认知过程的透明视图,进一步提高了可解释性。
2.2 基础
在本节中,我们介绍了使用LLMs进行思维链推理的初步知识,并引用了(Qiao等人,2023年)中的公式定义。假设有一个问题Q,一个提示T和一个概率语言模型PLM。模型将问题和提示作为输入,给出理由R和答案A。我们首先考虑上下文场景,其中演示不包含推理链。我们需要最大化答案A的可能性,如公式(1,2)所示。
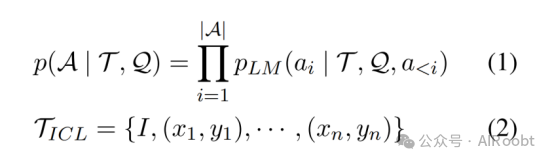
在思维链推理场景中,演示包含推理过程,我们需要最大化答案A和理由R的可能性,如公式(3,4,5,6)所示。
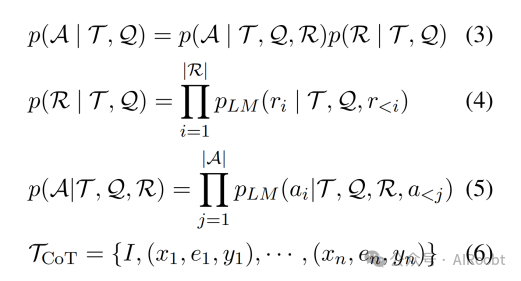
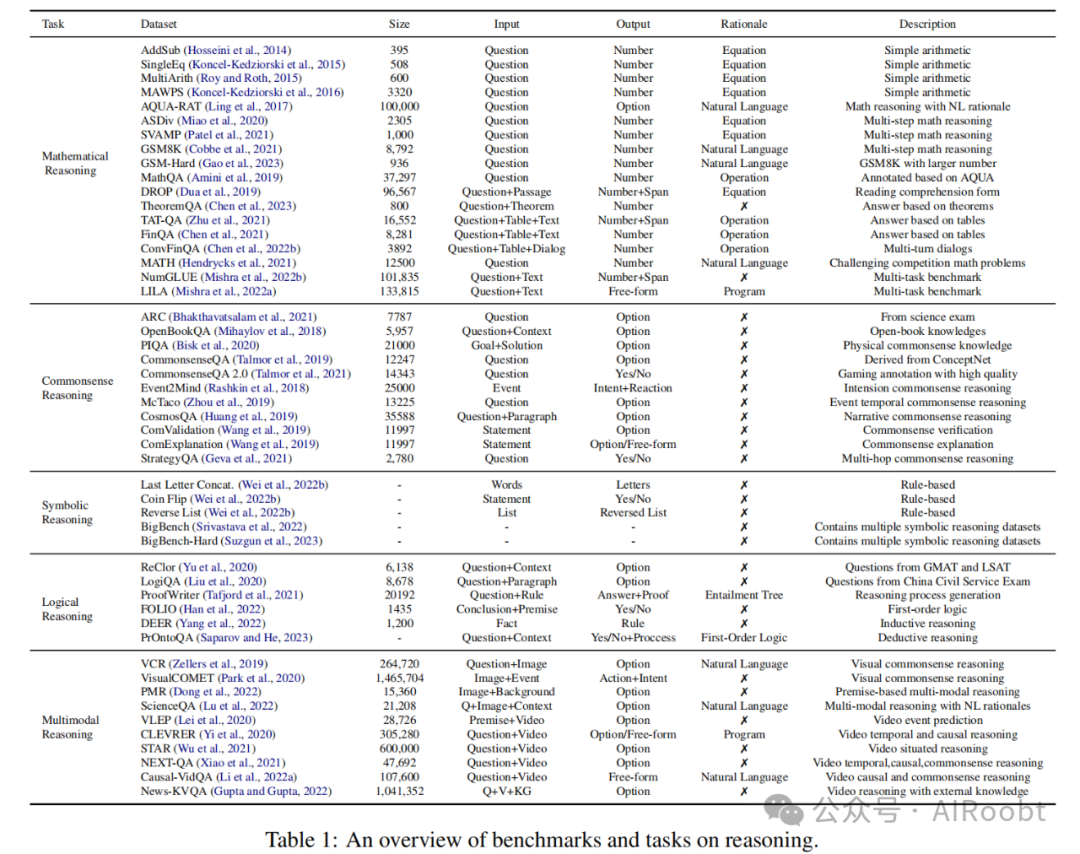
3 基准测试
3.1 数学推理
数学推理通常用来衡量模型的推理能力。早期的基准测试包含简单的算术运算(Hosseini等人,2014年;Koncel-Kedziorski等人,2015年;Roy和Roth,2015年;Koncel-Kedziorski等人,2016年)。Ling等人(2017年)以自然语言形式标记了推理过程,而Amini等人(2019年)在AQUA的基础上,通过以程序形式标记推理过程进行了构建。后来的基准测试(Miao等人,2020年;Patel等人,2021年;Cobbe等人,2021年;Gao等人,2023年)包含了更复杂和多样化的问题。(Zhu等人,2021年;Chen等人,2021年,2022b年)需要基于表格内容进行推理。还有一些通用基准测试(Hendrycks等人,2021年;Mishra等人,2022a,b年)和阅读理解形式的基准测试(Dua等人,2019年;Chen等人,2023年)。最近,(Yu等人,2021a年)通过使用层次推理和知识,赋予了预训练模型数学推理的能力。
3.2 常识推理
常识推理是基于通常在日常生活世界中普遍知晓和普遍感知的知识进行推断、判断和理解的过程。如何获取和理解常识知识是模型面对常识推理时面临的主要障碍。许多基准测试和任务都集中在常识理解上(Talmor等人,2019年,2021年;Bhakthavatsalam等人,2021年;Mihaylov等人,2018年;Geva等人,2021年;Huang等人,2019年;Bisk等人,2020年),事件时间常识推理(Rashkin等人,2018年;Zhou等人,2019年)和常识验证(Wang等人,2019年)。
3.3 符号推理
这里的符号推理特指模拟一些对人类来说简单但对LLMs来说具有挑战性的简单操作。最后一个字母串联、抛硬币和反转列表(Wei等人,2022b年)是最常用的符号推理任务。此外,协作基准测试BigBench(Srivastava等人,2022年)和BigBench-Hard(Suzgun等人,2023年)也包含了几个符号推理数据集,如状态跟踪和对象计数。
3.4 逻辑推理
逻辑推理分为演绎推理、归纳推理和溯因推理(Yu等人,2023a年)。演绎推理从一般前提中推导出结论(Liu等人,2020年;Yu等人,2020年;Tafjord等人,2021年;Han等人,2022年)。归纳推理从特殊案例中推导出一般结论(Yang等人,2022年)。溯因推理为观察到的现象提供合理的解释(Saparov和He,2023年)。
3.5 多模态推理
在现实世界中,推理还涉及除文本之外的其他模态信息,其中视觉模态最为普遍。为此,提出了许多视觉多模态推理的基准测试(Zellers等人,2019年;Park等人,2020年;Dong等人,2022年;Lu等人,2022年),其中ScienceQA(Lu等人,2022年)注释了推理过程,是使用最广泛的视觉多模态推理基准测试。视频多模态推理(Lei等人,2020年;Yi等人,2020年;Wu等人,2021年;Xiao等人,2021年;Li等人,2022a年;Gupta和Gupta,2022年)更具挑战性,因为它与视觉多模态推理相比引入了额外的时间信息。
3.6 指标
准确率 准确率用于评估模型在分类任务上的能力,通常用于多项选择(Ling等人,2017年;Mihaylov等人,2018年;Liu等人,2020年;Lu等人,2022年)和是非(Talmor等人,2021年;Geva等人,2021年;Han等人,2022年)任务。
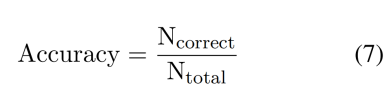
EM和F1 EM和F1是用于评估自由形式(Mishra等人,2022a年;Wang等人,2019年;Yi等人,2020年)和跨度提取(Dua等人,2019年;Zhu等人,2021年;Mishra等人,2022b年)任务的指标。两者都在词符级别上计算。
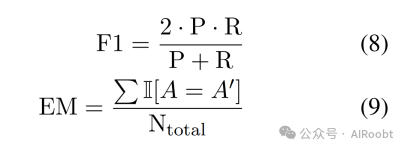
其中P和R分别代表精确度和召回率,EM计算预测和答案完全相同的比例。
4 方法
在本节中,我们通过三种不同的分类探讨X-of-thought(思维X)推理:X-of-thought的构建(4.1节)、X-of-thought的结构变体(4.2节)以及X-of-thought的增强方法(4.3节)。
4.1 构建方法
经过深入分析,我们将X-of-thought的构建分为三类:1)手动XoT,2)自动XoT,3)半自动XoT,具体描述如下。
4.1.1 手动XoT
尽管大型语言模型通过提示进行少量样本的上下文学习,但在推理任务中仍有限制。为了探索大型语言模型的潜在推理能力,一种标准方法是在示例中提供不同形式的思考。
Wei等人(2022b)首次提出思维链提示(Few-shot CoT),通过手动提供自然语言形式的理由来演示。为了进一步确保推理过程中的确定性并减少推理路径和答案之间的不一致性,PAL(Gao等人,2023)、PoT(Chen等人,2022a)和NLEP(Zhang等人,2023e)利用编程语言作为注释理由,将问题解决转化为可执行的Python程序。同时,为了同时利用自然语言和编程语言的优势并提高推理输出的置信度,MathPrompter(Imani等人,2023)使用零样本思维链提示生成多个代数表达式或Python函数,这些可以相互验证并提高结果的可靠性。此外,由于示例中的推理复杂性,如包含更多推理步骤的链,会导致性能提升,Fu等人(2023a)提出了基于复杂度的提示,其中在高复杂度理由之间进行投票以得出最终答案。
手动构建的X-of-thought方法通过向示例中添加不同类型的逐步中间推理过程来扩展上下文学习。它们允许LLMs模仿并生成推理路径。尽管手动XoT方法为人类理解和复杂任务(如数学推理、常识推理、符号推理等)提供了更大的可解释性和可靠性,但手动注释理由需要显著的成本,并存在诸如示范选择困难和任务泛化等缺点。具体来说,不同的任务需要不同方式的示范。因此,其他工作尝试自动构建推理路径,如在§4.1.2中讨论的。
4.1.2 自动XoT
思维链提示(Wei等人,2022b)通过在少量样本设置中使用特定任务示例激发了LLMs的复杂推理能力,这限制了可扩展性和泛化能力。为了减少手工制作的少量样本示例的成本,Kojima等人(2022)提出了零样本CoT,通过在问题后引入一个魔法短语“让我们一步步来”,使LLMs能够以零样本的方式生成推理链。然而,零样本CoT存在推理路径质量差、错误多的问题。由于示范的多样性在推理链生成中起着至关重要的作用,Auto-CoT(Zhang等人,2023f)通过聚类和代表性示例选择自动生成示范,提高了多样性并一致性地匹配或超过了Few-shot CoT的性能。COSP(Wan等人,2023)引入了问题的输出熵来辅助示范选择。Xu等人(2023)提出了Reprompting,通过迭代使用Gibbs采样来找到有效的CoT提示。同时,推理链中的一些错误来自遗漏步骤的错误,Wang等人(2023f)将零样本CoT扩展到计划和解决(PS)提示,通过设计一个计划将整个任务划分为更小的子任务,并根据计划执行子任务,带有更详细的指令。LogiCoT(Zhao等人,2023c)使用符号逻辑来验证零样本推理过程,从而减少推理中的错误。此外,PoT(Chen等人,2022a)也探索了语言模型,如Codex,通过添加“让我们一步步编写Python程序…”,在零样本设置中生成可执行的Python程序来解决数学问题,这减少了中间推理步骤中的错误。一些工作引入了代理来解决推理问题。例如,Agent Instruct(Crispino等人,2023a)利用代理生成与任务相关的、有信息量的指令,指导LLMs执行零样本推理。
与手动XoT不同,自动XoT使用零样本提示工程或采样,是可扩展的,并且可以在没有人类干预的情况下在领域之间泛化。然而,由于缺乏人类对齐,自动生成的思维链面临质量差、幻觉和事实不一致等挑战。因此,以半自动方式构建XoT是必要的,这在§4.1.3中介绍。
4.1.3 半自动XoT
半自动XoT方法结合了手动和自动构建方法的优点。Shao等人(2023)提出了合成提示,利用少数人工注释的示例来提示模型通过交替的前向-后向过程生成更多示例,并选择有效的示范以激发更好的推理,缓解了AutoCoT中缺乏人类对齐的问题。尽管之前的工作解决了手动注释的问题,示范选择也可以显著影响性能。Automate-CoT(Shum等人,2023)采用强化学习与方差降低的策略梯度策略来估计黑盒语言模型中每个示例的重要性,激发更好的示范选择。同样,Lu等人(2023b)提出了PromptPG,它利用策略梯度来学习在表格推理中选择示范。Ye和Durrett(2023)最初使用两个代理指标来评估每个示例,然后在示例中搜索以找到在银标开发集中产生最佳性能的示范。同时,Pitis等人(2023)提出了Boosted Prompting,这是一种提示集成方法来提高性能,它在遇到当前示范难以处理的问题时,通过迭代扩展示例。Zou等人(2023)引入了Meta-CoT,它根据问题类别自动选择示范,消除了特定任务提示设计的需求。
半自动XoT方法减少了手动标记的工作量,同时引入了人类对齐信号和示范选择策略,增强了推理的能力和稳定性。此外,它还实现了成本效益高的领域泛化。然而,示范选择问题尚未完全解决,需要更多的努力和研究。
4.2 XoT结构变体
最原始的思维链是一个链式结构,用自然语言描述中间推理步骤。在本节中,我们介绍修改原始链式结构的结构变体,包括链式结构变体、树状结构变体和图状结构变体。
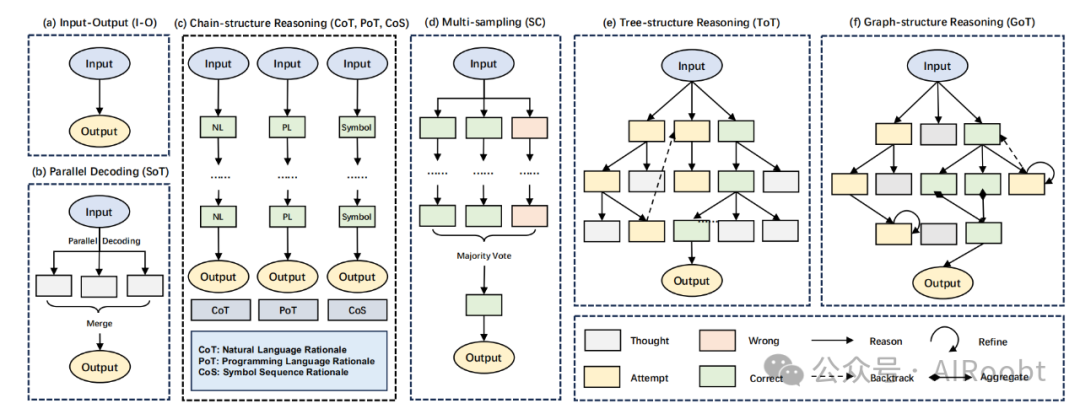
图2展示了推理的发展过程,从直接的输入/输出,到链式结构,再到树和图结构。
链式结构 PAL(Gao等人,2023年)和 PoT(Chen等人,2022a)引入编程语言来描述推理过程,从而将推理问题转化为可执行程序的实现,以获得最终答案。由于程序执行是确定性的并且能够准确执行算术计算,这种方法在数学推理中表现出色。此外,符号序列是另一种思维表示类型。符号链(Chain-of-Symbol,Hu等人,2023a)在规划期间用简化的符号链表示表示复杂环境,这减少了模拟环境的复杂性。链式结构变体如图2(c,d)所示。思维算法(Algorithm of Thought,Sel等人,2023)将算法能力注入模型,通过添加基于算法的示例使模型的推理更加逻辑化。它没有树搜索(Long,2023;Yao等人,2023b)的巨大搜索空间,节省了计算资源并取得了出色的性能。
树状结构 原始的链式结构本质上限制了探索范围。通过结合树状结构和树搜索算法,模型获得了在推理过程中有效探索和回溯的能力(Long,2023;Yao等人,2023b),如图2(e)所示。结合对中间思维的自我评估,模型可以实现全局最优解。ToT(思维链)的推理过程涉及不确定性,这可能导致级联错误。TouT(Mo和Xin,2023)在推理中引入了蒙特卡洛dropout,考虑了不确定性。Yu等人(2023b)深入研究了类似的问题,利用它们的解决方案提升LLMs复杂的推理能力。这些类似的问题呈现出树状结构,最终汇聚解决主要问题。然而,当前的思维树在选择任务上有很大的局限性,需要为每个任务设计特定的提示,这阻碍了它的广泛应用。SoT(Ning等人,2023)是树状结构的另一种变体,它将问题分解为可以并行处理并同时解决的子问题,以加快推理速度。然而,它的实用性仅限于可并行分解的问题,不适用于复杂推理任务。
图状结构 与树相比,图引入了循环和环,带来了更复杂的拓扑关系,并允许建模更复杂的推理,如图2(f)所示。GoT(Besta等人,2023;Lei等人,2023a)将中间思维视为图中的节点,结合探索和回溯操作,并与思维树相比额外引入了聚合和细化操作。额外的操作,聚合和细化,在复杂任务中激发了更好的推理。然而,它面临着与思维树相同的困境,即任务限制和较差的泛化能力。此外,它的推理成本增加了。与明确构建思维图的GoT不同,ResPrompt(Jiang等人,2023a)在提示文本中引入了思维之间的残差连接,允许不同步骤的推理相互交互。
随着模型从线性链过渡到层次化的树和复杂的图,思维的相互作用逐渐变得更加复杂,从而逐步增强了解决复杂问题的能力。然而,随着拓扑复杂性的增加,相关方法对任务选择施加了更多限制,导致它们的泛化能力显著降低,使其应用变得困难。将基于复杂拓扑结构的方法扩展到通用领域是未来研究面临的一个主要挑战。
4.3 XoT增强方法
在本节中,我们将介绍XoT增强方法。总共,我们将提供五个类别的概述,分别是添加验证和细化(4.3.1节)、问题分解(4.3.2节)、利用外部知识(4.3.3节)、投票和排名(4.3.4节)以及提高效率(4.3.5节)。
4.3.1 验证和改进
思维链推理往往倾向于产生幻觉,产生错误的推理步骤。中间推理步骤中的错误又可能触发一系列错误。引入验证以获得反馈,随后根据这些反馈细化推理过程,可以有效地减轻这种现象,类似于人类反思的过程。图3描述了验证和细化的概述。
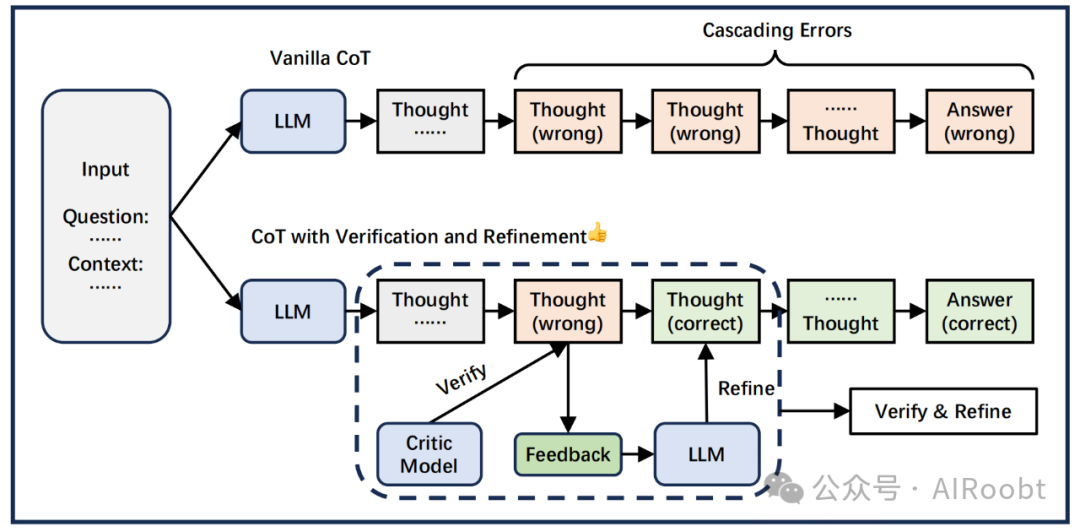
图3:验证和改进减少推理中的级联错误。
VerifyCoT(Ling等人,2023年)设计了一种自然程序,这是一种演绎推理形式,允许模型产生准确的推理步骤,每个后续步骤严格基于前一步。DIVERSE(Li等人,2022c)使用投票机制来排除错误答案,然后对每个推理步骤进行细粒度的验证。SCREWS(Shridhar等人,2023)认为后修改的结果并不一定优于原始结果,因此它引入了一个选择模块来在原始和修改之间选择更好的结果。为了便于知识密集型任务,Verify-and-Edit(Zhao等人,2023a)引入外部知识来重新推理不确定的示例,减少推理中的事实错误。一些研究努力尝试挖掘模型的内部知识。为了解决事实错误,一些研究尝试挖掘LLMs的内在知识。他们在回答问题之前从模型中获取知识(Dhuliawala等人,2023年;Zheng等人,2023年)。Ji等人(2023年)进一步验证了内在知识的正确性,Liu等人(2023b)通过强化学习提高了内在知识获取的准确性。
不一致性是推理中的另一个主要挑战,Dua等人(2022年)迭代地使用先前的推理结果作为提示,直到模型给出一致的答案。Paul等人(2023年)训练一个批评模型来提供关于推理过程的结构化反馈。Self-Refine(Madaan等人,2023)执行迭代自我反馈和细化以减轻推理中的错误。与Self-Refine相比,Reflexion(Shinn等人,2023)引入了强化学习进行反思,这也带来了决策能力。同时,一些工作引入了反向推理(Yu等人,2023a)进行验证。
RCoT(Xue等人,2023)根据推理链重构问题,其与原始问题的不一致性暴露了推理过程中的错误。FOBAR(Jiang等人,2023b)和Self Verification(Weng等人,2022)通过从答案中推断问题中的条件进行验证。FOBAR推断问题中的变量,而Self Verification推断问题中的条件。然而,Huang等人(2023a)发现LLMs在没有外部反馈的情况下难以自我纠正,甚至可能导致性能下降。
LLM推理是一个无监督过程,在中间推理步骤中来自反馈信号的指导在提高推理中起着至关重要的作用。来自反馈信号的指导可以有效地减少推理中的幻觉现象。在获取适当的反馈并根据该反馈进行准确纠正方面仍有很大的研究空间。
4.3.2 问题分解
X-of-thought推理的本质在于其逐步解决问题。然而,原始的思维链推理方法并没有明确地剥离出逐步推理过程,仍然使用一次性生成。在本节中,我们将讨论问题分解方法,该方法明确地逐步解决问题。概述如图4所示。
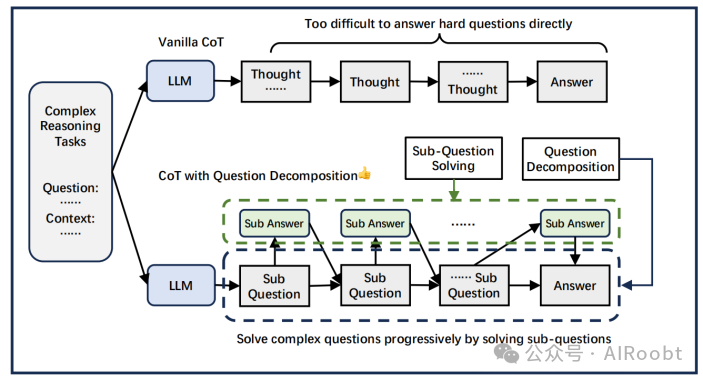
图 4:问题分解通过逐步解决简单的子问题来解决复杂问题。
Wang等人(2022a)迭代地从模型中获取知识,在多跳QA中取得进展。Zhou等人(2023b)提出了Least-to-Most提示,最初以自顶向下的方式将问题分解为子问题,随后,它一次解决一个子问题,并利用它们的解决方案来促进后续子问题。Successive Prompting(Dua等人,2022)采取了与Least-to-Most提示类似的方法,不同之处在于它采用了交错的子问题和答案的分解,而不是两阶段分解。上述方法没有为各种子问题制定定制解决方案。Decomposed Prompting(Khot等人,2023)设计了一个模块化共享库,每个库专门针对一类子问题,可以为不同类别的子问题定制更有效的解决方案。除了一般任务,一些工作专注于表格推理中的问题分解。BINDER(Cheng等人,2023)以神经符号方式将推理映射到程序,并通过程序执行器(如Python或SQL)获得最终答案。Ye等人(2023)引入了DATER,它将大型表格分解为较小的表格,将复杂问题分解为简单问题。前者减少了不相关信息,后者减少了推理的复杂性。
直接回答复杂问题可能是具有挑战性的。通过将问题分解为简单的子问题并逐步解决它们,难度降低了。此外,每个子问题都可以追溯到特定的推理步骤,使推理过程更加透明和可解释。当前的工作大多使用自顶向下的分解策略,而基于反向推理的自底向上分解策略仍有待在未来的工作中探索。
如何系统的去学习大模型LLM ?
作为一名热心肠的互联网老兵,我意识到有很多经验和知识值得分享给大家,也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑,所以在工作繁忙的情况下还是坚持各种整理和分享。
但苦于知识传播途径有限,很多互联网行业朋友无法获得正确的资料得到学习提升,故此将并将重要的 AI大模型资料 包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


