- 1conda 安装opencv_基于python和OpenCV构建智能停车系统
- 2华为OD机试C卷-- 最长子字符串的长度(二)(Java & JS & Python & C)_华为机考最长子字符串的长度2
- 3菜鸟写Python-Scrapy:Spider源码分析_valueerror: spider must have a name
- 4【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 异国客人的幸运数字 (100分) - 三语言AC题解(Python/Java/Cpp)
- 5最新版gradle安装使用简介_gradle 6.7
- 6分布式锁全面总结_分布式锁机制
- 7软件测试|自动化界面操作神器pywinauto教程(一)
- 8【AI大模型应用开发】从CoT到ToT,再到ReAct,提升大模型推理能力的方式探索(含代码)_cot totreact
- 9Yolov7/Yolov5损失函数改进:Wasserstein Distance Loss,助力小目标涨点
- 10什么是shuffle?shuffle的原理及过程
聚类算法 | Kmeans:肘方法、Kmeans++、轮廓系数 | DBSCAN_聚类肘部判别法
赞
踩
本篇文章我们来讲机器学习篇章中的最后一个专题:聚类算法
那么,什么是聚类呢?
聚类(Clustering):
按照某个特定标准(如距离),把一个数据集分割成不同的类或簇
使同一个簇内的数据对象相似性尽可能大
不在同一个簇中的数据对象差异性也尽可能地大
即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离
- 1
- 2
- 3
- 4
- 5
简单说,聚类算法就是物以类聚,人以群分
注意:聚类算法是机器学习篇中接触到的第二个无监督算法(前面讲过PCA)
一. 聚类算法划分方式
1. 划分式
- K-Means算法(均值)
- K-medoids算法(中值)
- K-modes算法(众数)
- K-prototypes算法
- CLARANS(基于选择)
- K-Means++
- bi-KMeans
2. 层次式
- BIRCH算法(平衡迭代规约)
- CURE算法(点聚类)
- CHAMELEON(动态模型)
- Agglomerative(凝聚式)
- Divisive(分裂式)
3. 基于密度
- DBSCAN(基于密度连接区域)
- DENCLUE(密度分布函数)
- OPTICS(对象排序识别)
4. 基于网络
- STING(统计信息网络)
- CLIOUE(聚类高维空间)
- WAVE-CLUSTER(小波变换)
5. 基于模型
- 统计学方法(比如GMM)
- 神经网络(比如SOM(Self Organized Maps))
二. K-means算法
牧师村民模型:
有四位牧师前往乡村布道。起初,他们随意选择了几个布道点,并向乡村所有村民公布了这些点的情况。于是,每位村民都前往离家最近的布道点听课
听完课后,大家觉得距离太远了。于是每位牧师统计了自己所有听课村民的地址,并搬到了这些地址的中心地带。他们在海报上更新了自己的布道点位置
每次移动后,牧师不可能让所有人都更近。有些人发现A牧师搬迁后,去B牧师那听课反而更近。于是每位村民又选择了离自己最近的布道点
牧师每周更新位置,村民根据情况选择布道点,最终实现了稳定
上述过程我们用图像描述如下:
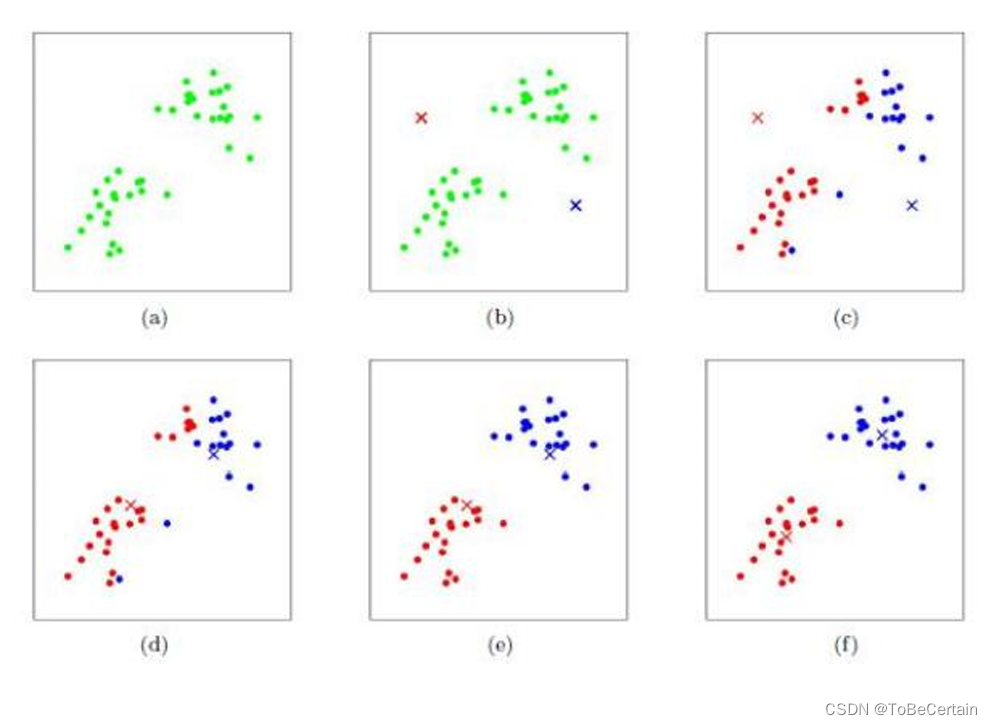
这里补充:【Kmeans聚类的可视化演示】
1. K-means算法公式表达
算法评价:算法简单,聚类效果好,即使是在巨大的数据集上也非常容易部署实施
K-Means算法有大量的变体
包括:初始化优化K-Means++ 以及大数据应用背景下的 k-means|| 和 Mini Batch K-Mean
- 1
- 2
- K-Means算法操作:按照样本之间的距离大小,将样本集划分为 K 个簇
- 目的:让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
用数学表达式表示,假设簇划分为 ( C 1 , C 2 , … C k ) \left(C_{1}, C_{2}, \ldots C_{k}\right) (C1,C2,…Ck) ,则我们的目标是最小化平方误差 E \mathrm{E} E :
E = ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 2 E=\sum_{i=1}^{k} \sum_{x \in C_{i}}\left\|x-\mu_{i}\right\|_{2}^{2} E=i=1∑kx∈Ci∑∥x−μi∥22
其中 μ i \mu_{i} μi 是簇 C i C_{i} Ci 的均值向量,有时也称为质心,表达式为:
μ i = 1 ∣ C i ∣ ∑ x ∈ C i x \mu_{i}=\frac{1}{\left|C_{i}\right|} \sum_{x \in C_{i}} x μi=∣Ci∣1x∈Ci∑x
2. K-means算法流程
输入:样本集
D
=
{
x
1
,
x
2
,
…
.
x
N
}
D=\left\{x_{1}, x_{2}, \ldots . x_{N}\right\}
D={x1,x2,….xN} , 聚类的簇数
k
k
k ,最大迭代次数
T
T
T
输出:簇划分
C
=
{
C
1
,
C
2
,
…
C
k
}
C=\left\{C_{1}, C_{2}, \ldots C_{k}\right\}
C={C1,C2,…Ck}
具体操作:
-
从数据集 D \mathrm{D} D 中随机选择 k \mathrm{k} k 个样本作为初始的质心向量,即 { μ 1 , μ 2 , … , μ k } \left\{\mu_{1}, \mu_{2}, \ldots, \mu_{\mathrm{k}}\right\} {μ1,μ2,…,μk} ,将每个簇初始化为空集
-
当迭代次数 t = 1 , 2 , … , T ) t=1,2, \ldots, \mathrm{T} ) t=1,2,…,T)
a):计算样本 x i x_{i} xi 到各个质心向量 μ j \mu_{j} μj 的欧式距离
b):将 x i x_{i} xi 划分到最近的簇中,即更新 C j = C j ∪ { x i } C_{\mathrm{j}}=\mathrm{C}_{\mathrm{j}} \cup\left\{\mathrm{x}_{\mathrm{i}}\right\} Cj=Cj∪{xi}
c):重新计算 C j C_{j} Cj 中所有样本点的质心
μ j = 1 ∣ C j ∣ ∑ x ∈ C j x \mu_{j}=\frac{1}{\left|C_{j}\right|} \sum_{x \in C_{j}} x μj=∣Cj∣1x∈Cj∑xd):只有当 k \mathrm{k} k 个质心向量都没有发生变化,则转到步骤3
-
输出簇划分 C = { C 1 , C 2 , … C k } C=\left\{C_{1}, C_{2}, \ldots C_{k}\right\} C={C1,C2,…Ck}
3. Kmeans算法缺点
-
聚类中心的个数K需要事先给定
但实际中K值的选定是非常困难的,很多时候我们并不知道给定的数据集应该聚成多少个类别才最合适 -
Kmeans算法需要随机地确定初始聚类中心
不同的初始聚类中心可能导致完全不同的聚类结果,有时会导致算法收敛很慢甚至出现聚类出错的情况
3.1 肘方法
针对第一个缺点,通常我们会根据先前的经验选择一个合适的k值,如果没有先验知识,则可以使用“肘方法”来选择一个合适的k值
肘方法,也称为手肘法或Knee of SSE,是用于确定聚类算法中最优聚类数(K值)的一种启发式方法
核心概念:在聚类分析中,特别是在K-means聚类算法中,我们需要预先指定簇的数量K。为了找到最佳的K值,通常会使用误差平方和(SSE)作为评估标准
操作方式:随着聚类数量K的增加,样本会被划分得越来越精细,每个簇内的紧密程度提高,因此SSE会逐渐减小
当K值小于实际的聚类数量时,增加K会显著降低SSE
当K值达到实际聚类数量后,再增加K,SSE的下降速度会突然减慢
实际应用:在实践中,通过计算不同K值对应的SSE,并将这些点绘制在图表上,寻找“肘部”出现的点
即:SSE下降速度减缓的转折点,该点的K值通常被认为是数据集中真实的聚类数量
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
讲该方法抽象为数学公式:
S
S
E
=
∑
i
=
1
k
∑
p
∈
C
i
∣
p
−
m
i
∣
2
SSE=\sum_{i=1}^{k} \sum_{p \in C_{i}}\left|p-m_{i}\right|^{2}
SSE=i=1∑kp∈Ci∑∣p−mi∣2
其中 C i C_{i} Ci 为第 i i i 个簇, m i m_{i} mi 为第 i i i 个质心, p p p 为属于 C i C_{i} Ci 的数据点,SSE代表了聚类效果
3.2 k-means++ 算法
针对第二个缺点:可以通过k-means++算法来解决,即对于初始化质心的优化策略
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心 μ 1 μ1 μ1
- 对于数据集中的每一个点 x i x_{i} xi,计算到已选择中心点的最近聚类中心的距离D
- 选择一个新的数据点作为新的聚类中心,选择的原则是:
D较大的点,被选取作为聚类中心的概率较大 - 重复2和3,直到选择出k个聚类质心
- 利用这k个质心来作为初始化质心,运行标准的K-Means算法
这里对下一个聚类中心点的选举方式做解释:
- 对于距离最远的样本点,可能是离群点
- 对于单个最远距离的离群点,其概率或许很大;但整体看待一个簇的概率时,单个离群点的概率就很小
3.2.1 k-means|| 算法
k-means||是k-means++的变体,k-means||在初始化中心点时对kmeans++的缺点做了
规避,主要体现在:
不需要根据k的个数严格地寻找k个点
主要思路:
改变每次遍历时的取样规则
每次获取 K个样本,重复该取样操作O(logn)次
将这些抽样出来的样本聚类出K个点
- 1
- 2
- 3
- 4
- 5
- 6
使用这K个点作为K-Means算法的初始聚簇中心点(实践证明:一般5次重复采用就可以保证一个比较好的聚簇中心点)
3.3 Mini Batch K-Means 算法
在传统的K-Means算法中,要计算所有的样本点到所有的质心的距离,如果样本量非常大,算法非常耗时;因此,在海量数据面前,Mini Batch K-Means应运而生
-
Mini Batch操作:
用样本集中的一部分的样本来做传统的K-Means,避免样本量太大时的计算难题,同时算法收敛速度也大大加快选择一个合适的批样本大小batch size,用batch size个样本来做K-Means聚类 对于batch size:一般是通过无放回的随机采样得到的- 1
- 2
- 3
-
Mini Batch代价:
聚类的精确度会有一些降低,一般来说这个降低的幅度在可以接受的范围之内
4. 聚类评估
- 簇内不相似度:计算样本
i
i
i到同簇其它样本的平均距离为
a
i
a_{i}
ai
a i a_{i} ai越小,表示样本 i i i 越应该被聚类到该簇
簇 C C C 中的所有样本的 a i a_{i} ai的均值被称为簇 C C C的凝聚度
-
簇间不相似度:计算样本 i i i到最近簇 C j C_{j} Cj(非自身所在簇)所有样本的平均距离 b i b_{i} bi
具体:计算所有簇中样本到样本 i i i的平均距离,取距离最小的簇b i b_{i} bi越大,表示样本 i i i越不属于其它簇
-
轮廓系数: s i s_{i} si 取值范围为 [ − 1 , 1 ] [-1,1] [−1,1]
越接近1表示样本 i i i聚类越合理
越接近-1,表示样本 i i i应该分类到另外的簇中
近似为0,表示样本 i i i应该在边界上
所有样本 s i s_{i} si的均值被称为聚类结果的轮廓系数
s ( i ) = b ( i ) − a ( i ) max { a ( i ) , b ( i ) } s(i)=\frac{b(i)-a(i)}{\max \{a(i), b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)
s
(
i
)
=
{
1
−
a
(
i
)
b
(
i
)
,
a
(
i
)
<
b
(
i
)
0
,
a
(
i
)
=
b
(
i
)
b
(
i
)
a
(
i
)
−
1
,
a
(
i
)
>
b
(
i
)
s(i)=\left\{
补充:当簇中存在异常点时,使用K-Mediods聚类(K中值聚类)的效果优于Kmeans
三. DBSCAN算法
基于距离的聚类算法对于球状簇的聚类效果并不好
而对于基于密度的聚类算法,聚类形状可以为任意形状:
通过在数据集中寻找被低密度区域分离的高密度区域,将分离出的高密度区域作为一个独立的类别
- 1

DBSCAN,即Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法,是基于密度空间的聚类算法
具体原理:
每个簇类的密度高于该簇类周围的密度
噪声的密度小于任一簇类的密度
因此DBSCAN算法也能用于异常点检测
- 1
- 2
- 3
- 4
- 5
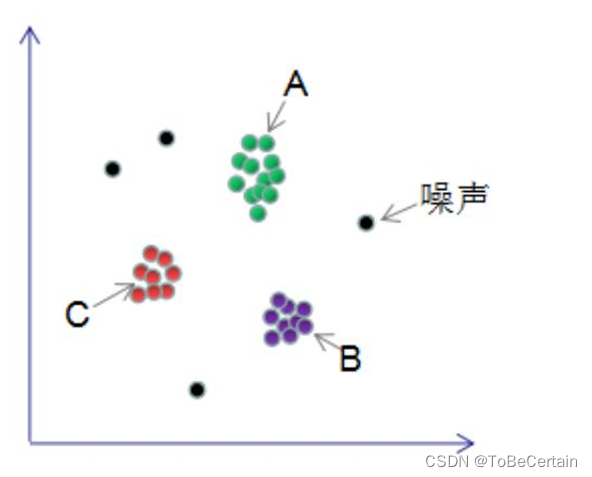
1. DBSCAN算法组成
DBSCAN算法处理后的聚类样本点分为:
- 核心点(core points)
- 边界点(border points)
- 噪声点(noise)
超参数:距离 Ɛ Ɛ Ɛ 和 邻居数目 M i n P t s MinPts MinPts
1.1 核心点
对某一数据集 D D D,若样本 p p p的 ε \varepsilon ε - 邻域内至少包含MinPts个样本(包括样本 p p p),那么样本 p p p称核心点。即:
N ε ( p ) ≥ MinPts N_{\varepsilon}(p) \geq \operatorname{MinPts} Nε(p)≥MinPts
其中 ε \varepsilon ε - 邻域 N ε ( p ) N_{\varepsilon}(\mathrm{p}) Nε(p) 的表达式为:
N ε ( p ) = { q ∈ D ∣ dist ( p , q ) ≤ ε } N_{\varepsilon}(p)=\{q \in D \mid \operatorname{dist}(p, q) \leq \varepsilon\} Nε(p)={q∈D∣dist(p,q)≤ε}
1.2 边界点
若样本 b b b 在任意核心点 p p p 的 Ɛ Ɛ Ɛ- 邻域内,但是它的 Ɛ Ɛ Ɛ- 邻域内的样本数少于 M i n P t s MinPts MinPts(包括样本p),那么样本b称为边界点
1.3 噪声点
如果样本n既不是核心点,也不是边界点,则称为噪声点
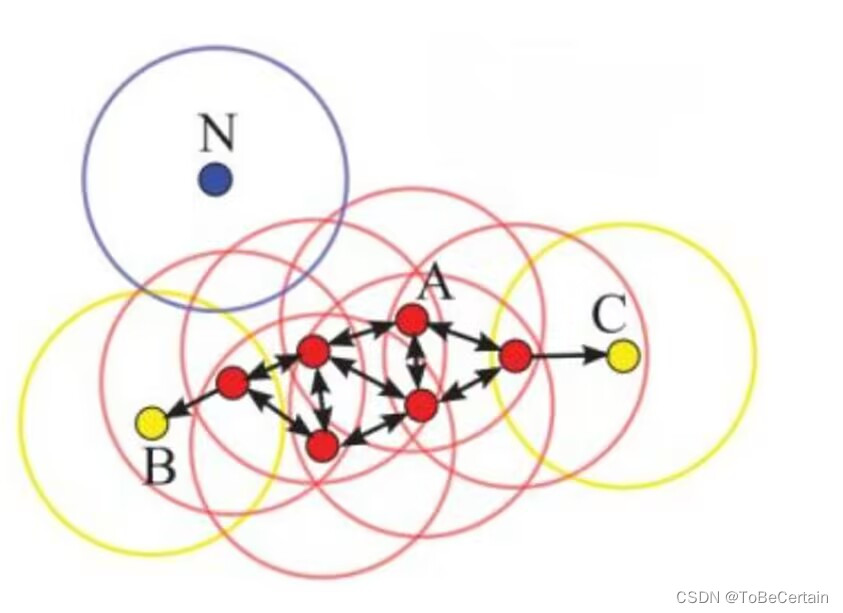
假设 M i n P t s = 4 MinPts = 4 MinPts=4
红色:核心点
黄色:边界点
蓝色:噪声点
2. DBSCAN算法原理
-
密度直达(directly density-reachable)
若 p p p为核心点, q q q处于 p p p的 Ɛ Ɛ Ɛ- 邻域内,则称 q q q由 p p p密度直达 -
密度可达(density-reachable)
若 p 1 , p 2 , . . . , p n p_{1},p_{2},...,p_{n} p1,p2,...,pn 均为核心点,且 p i p_{i} pi由 p i + 1 p_{i+1} pi+1密度直达(因此
p i + 1 p_{i+1} pi+1由 p i p_{i} pi密度直达),则称 p 1 , p 2 , . . . , p n p_{1},p_{2},...,p_{n} p1,p2,...,pn两两之间均密度可达 -
密度相连(density-connected)
若 p p p和 q q q密度可达,则 p p p的 Ɛ Ɛ Ɛ-邻域内的任何点与 q q q的 Ɛ Ɛ Ɛ-邻域内的任何点都密度相连
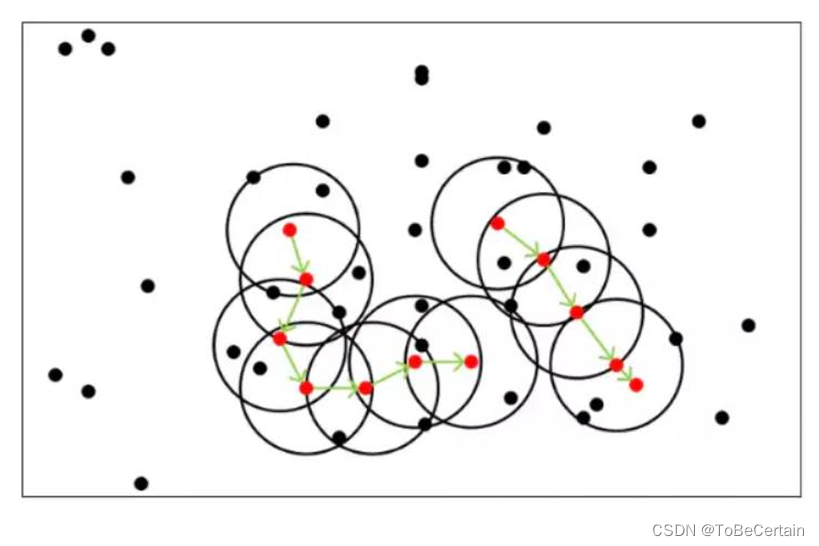
假设MinPts=5 红色:核心点 黑色:不是核心点 所有由核心点密度直达的点,都在以该核心点为中心的超球体内 反之,如果某个点不能密度直达,则不在超球体内 绿色箭头连接起来的核心点组成了密度可达的样本序列 在密度可达的样本序列的 Ɛ- 邻域内,所有的样本相互都是密度相连的- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
只要两个样本点是密度相连的关系,那么该两个样本点归为同一簇类
3. DBSCAN算法流程
从数据集D中随机选择一个核心点作为“种子”,由该种子出发确定相应的聚类簇,当遍历完与之密度可达的所有核心点时,一次聚类结束
- 1
-
任意选取一个点:
以该点为中心,找到与这个点距离 ≤ Ɛ \leƐ ≤Ɛ 的所有的点如果数据点个数 < < < MinPts,那么这个点被标记为噪声 / 边界点
如果数据点个数 ≥ \ge ≥ MinPts,那么这个点被标记为核心样本,并被分配一个新的簇标签 -
访问该点在 Ɛ Ɛ Ɛ内的所有邻居:
如果样本点还没有被分配一个簇,那么就将刚刚创建的新簇标签分配给它们
如果它们是核心样本,那么就依次访问其邻居,以此类推
簇逐渐增大,直到在簇的 Ɛ Ɛ Ɛ 距离内没有更多的核心样本为止 -
选取另一个尚未被访问过的点,并重复相同的过程
4. DBSCAN 超参数选择
Ɛ 设置得非常小,则意味着没有点是核心样本,可能会导致所有点被标记为噪声
Ɛ 设置得非常大,可能会导致所有点形成单个簇
Ɛ 可以隐式地控制簇的个数
使用 StandarScaler 或 MinMaxScaler 对数据进行缩放,有时更容易找到 Ɛ 的较好取值;因为使用缩放技术将确保所有特征具有相似的范围
- 1
- 2
- 3
- 4
- 5
感谢阅读 本文内容由网友自发贡献,转载请注明出处:https://www.wpsshop.cn/w/寸_铁/article/detail/773394
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


