2020年五一杯数学建模C题饲料混合加工问题解题全过程文档及程序_饲料加工厂需要加工一批动物能量饲料。饲料加工需要原料,如加工猪饲料需要玉米、

2020年五一杯数学建模

C题 饲料混合加工问题

原题再现

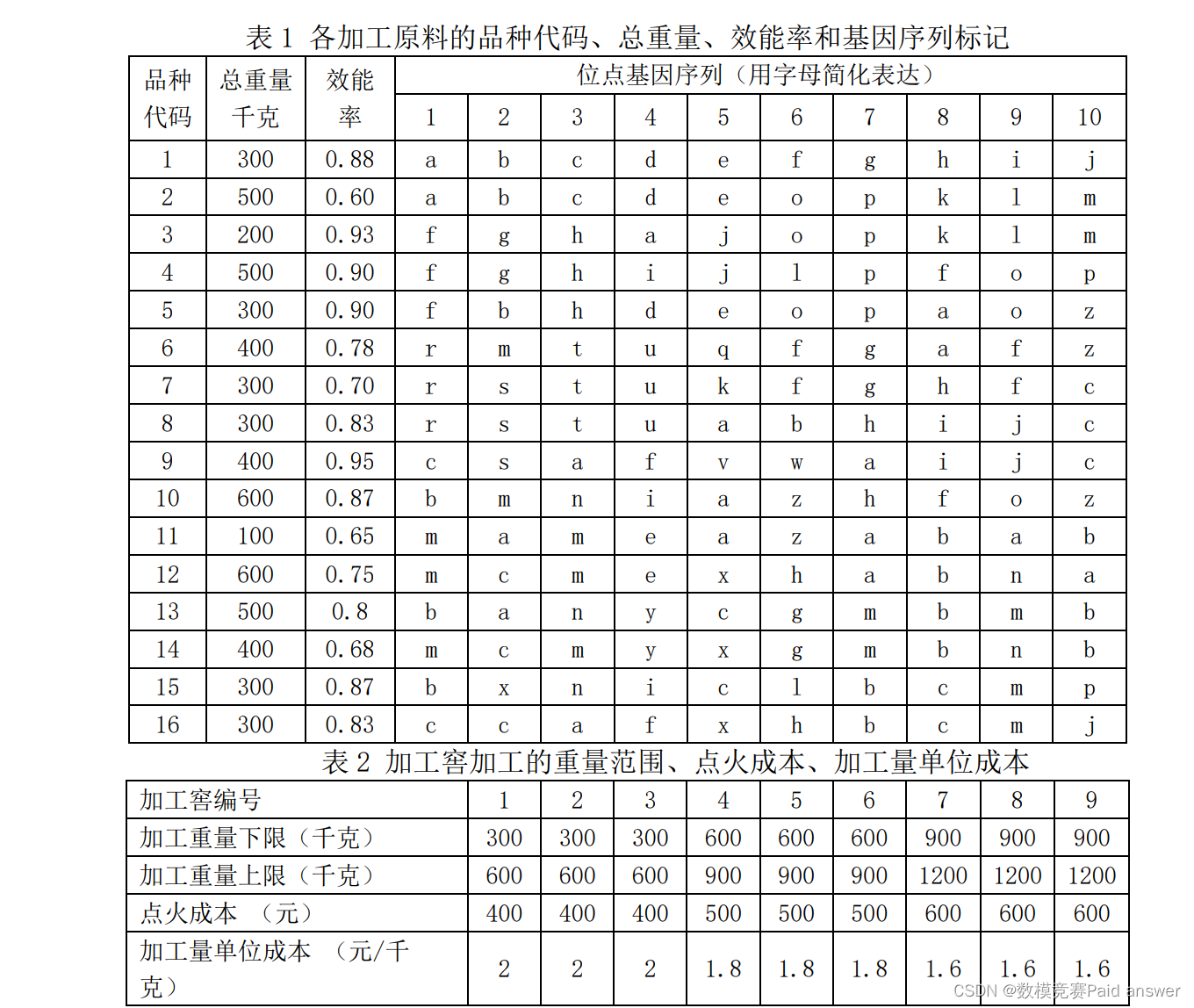
  饲料加工厂需要加工一批动物能量饲料。饲料加工需要原料，如加工猪饲料需要玉米、荞麦、稻谷等。加工厂从不同的产区收购了原料，原料在收购的过程中由于运输、保鲜以及产品本身属性等原因，存在着效能率的问题（如1吨玉米可加工成0.7吨左右的玉米面）。这个数据在原料进厂之后可以通过随机抽样进行检测得到。
  某饲料加工厂有9个加工窖，现有一批加工任务，要将16个加工原料（见表1）按照某种混合方案一次性放入加工窖中进行加工。一个加工窖的混合产品称为一个加工包。如果某加工原料重量不少于500千克，则可以单独成为一个加工包。因产品属性原因，要求品种代码10的加工原料不能单独成为一个加工包。每一个加工窖能够加工的重量有限定范围（见表2）。加工窖加工成本由点火成本（也称固定成本）与加工量成本（也称可变成本）构成，其他成本暂不考虑。表1提供了各加工原料的品种代码、总重量和效能率。表2提供了每一个加工窖能够加工的重量范围以及点火成本、加工量单位成本数据。
  由于加工窖数量低于饲料加工原料的品种数，所以在加工前需要将若干个加工原料进行混合。为了保证加工后饲料的质量，要求混合的任何两个加工原料之间必须具有亲缘关系。工厂技术人员对每种加工原料进行了基因检测，得到了10个关键位点的基因序列（见表1），并规定，两个加工原料如果有N个相同位点的基因序列标记相同，就认为这两个加工原料的亲缘值为N（如果N大于0，则说明这两种加工原料之间具有亲缘关系），一个加工包中所有原料两两之间亲缘值的平均值称为亲缘度。例如品种代码1、2、5的加工原料混合成为一个加工包，假设品种代码1和品种代码2的亲缘值为5，品种代码1和品种代码5的亲缘值为3，品种代码2和品种代码5的亲缘值为5，那么它们的亲缘度就是(5+3+5)/3。如果一个加工包中只含有一种加工原料，则该加工包的亲缘度为10。本题仅从亲缘度角度考虑混合加工饲料的质量，亲缘度越高，饲料质量就越高。
  请考虑下列问题：
  1. 请研究16个加工原料两两之间的亲缘值，并进行统计性分析。
  2. 将16个加工原料进行混合全部放入9个加工窖中。请建立数学模型，求出饲料质量最高的混合方案并给出每个加工包的亲缘度。
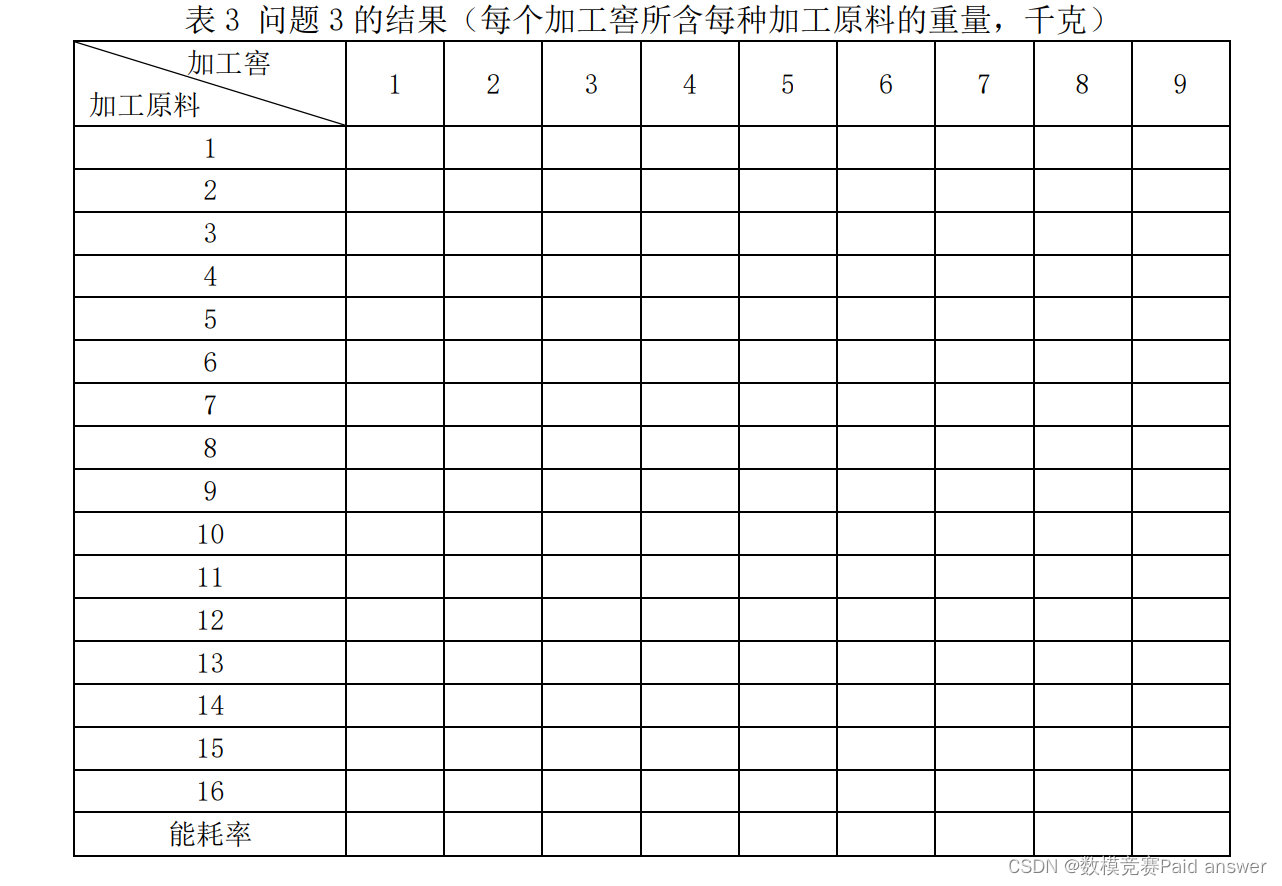
  3. 将16个加工原料进行混合全部放入9个加工窖中。请建立数学模型，求出平均能耗率超过80%的加工包数量最多的混合方案并给出每个加工包的能耗率，并将结果填入表3。
  4. 如果饲料加工厂允许部分加工窖不生产，请建立数学模型，给出混合加工方案，用尽量低的加工成本完成整个加工任务，同时要求平均能耗率超过80%的加工包尽量的多。
  5. 如果饲料加工厂允许部分加工窖不生产，但必须完成整个加工任务。请建立数学模型，给出混合加工方案使得（1）饲料质量尽量高，（2）加工成本尽量低，（3）平均能耗率超过80%的加工包尽量多。

整体求解过程概述(摘要)

  近年来，养殖业迅猛发展，对于饲料的需求日益增加，导致饲料混合加工行业竞争十分激烈。因此，企业都在积极寻求质优价廉高效的饲料配比方案。本文通过数学模型，就饲料配比加工方案进行优化，给出最优的饲料混合配比方案。
  针对问题一，对饲料两两加工原料之间的亲缘关系进行研究。饲料两两加工原料之间的亲缘关系用两种原料的对应 10 个关键点的基因序列相同个数进行判断，其表征为亲缘值大小。利用 Matlab 进行编程，获得两两加工原料的亲缘值表。对两两加工原料亲缘关系利用 IBM SPSS statistics 进行统计分析获得两两加工原料亲缘关系有 40 种，最大值为 6，最小值为 1，亲缘值范围长度为 5，亲缘值方差为 2.254，标准偏差为 1.50128，均值为 3.0500。
  针对问题二，要求将 16 种加工原料全部放入 9 个加工窖中进行加工，求出能得出饲料质量最高的混合并给出每个加工包的亲缘度，实际上是一个优化问题。以加工原料的混合配比方案的亲缘度为优化目标。假设所有加工窖在加工过程中完全可以正常使用；只考虑亲缘度对混合加工饲料质量的影响；假设只考虑加工窖的点火成本和加工量成本，其他成本不考虑。建立亲缘度优化目标函数，给出配比方案的质量系数矩阵 A,在满足加工窖质量上下限约束和特定种类不能单独混合约束条件下，通过 Matlab 编程，结合蒙特卡洛算法进行优化，得到亲缘度最大的原料混合配比加工方案，亲缘度的最大值为 50.667。
  针对问题三，要求将 16 个加工原料进行混合全部放入 9 个加工窖中，求出平均效能率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率，也是最优问题，优化目标函数为加工包的能耗率最大问题。影响单个加工包效能率的因素为每个加工窖中的每种加工原料的质量分配。在问题 2 的基础之上结合题目三所给的约束条件进行求解。利用蒙特卡洛算法进行优化，得到平均能耗效率超过 0.8 的加工包有 7 个 ，另外两个加工包的效率也在 0.7-0.8 之间。
  针对问题四，从本质上来说，问题 4 属于双目标优化问题，问要求在允许部分加工窖不生产的情况下，满足成本尽量低，平均效能率超过 80%的加工包尽量多，取消一次性加工限制，可以多次加工。即在各种约束条件下设计出一个可以使得成本最小化、平均效能率超过 80%的加工包尽量多的混合方案。建立成本最低，加工包能耗率大于 0.8 数量尽可能多的目标函数，利用线性加权和法进行双目标优化，经过优化得线性加权和后的目标函数的最优解为 0.9548，其中成本为14350 元，效能值大于 0.8 的加工包的数量为 5。
  问题五与问题四类似，属于多目标优化问题。经优化得线性加权后得目标函数得最优解为 0.9091，在此种配比情况下亲缘值为 43，即为质量最好，成本为14474 元，效能率大于 0.8 的加工包数量为 4。

模型假设：

  [1]假设所有加工窖在加工过程中完全可以正常使用。
  [2]假设只考虑亲缘度对混合加工饲料质量的影响。
  [3]假设只考虑加工窖的点火成本和加工量成本，其他成本不考虑。

问题分析：

  问题 1 的分析
  问题 1 要求研究 16 个加工原料两两之间的亲缘值，并进行统计性分析。因此，首先根据题目所给亲缘值定义：即两个加工原料如果有 N 个相同位点的基因序列标记相同，就认为这两个加工原料的亲缘值为 N（如果 N 大于 0，则说明这两种加工原料之间具有亲缘关系）。由于是两两原料之间，且两元素之间不存在先后顺序问题，所以利用 matlab 进行编程，筛选出两两加工原料的组合方式，并计算出两两加工原料之间的亲缘值，然后利用 IBM SPSS Statistics 对数据进行统计分析。
  问题 2 的分析
  问题 2 要求将 16 种加工原料全部放入 9 个加工窖中进行加工，建立数学模型，求出能得出饲料质量最高的混合并给出每个加工包的亲缘度。显然问题二最终目标是求取亲缘度最优值问题，并给出饲料质量最高的混合方案（仅从亲缘度角度考虑混合加工饲料的质量，亲缘度越高，饲料质量就越高）。将 16 中种加工原料进行混合投放到 9 个加工窖中进行加工，由于每个加工窖中投放的加工原料组合不同以及每种组合方式的加工原料的重量分配比例也不确定，因此每个加工窖的加工原料组合具有随机性。因此我们将加工窖中加工原料混合方案问题看作是蒙特卡洛算法的优化组合方案问题。在考虑加工原料混合方案时，如何确定每一个加工窖的投放的加工原料的种类以及各种加工原料的重量占比是本问题的难点。但是，从企业的经营方式和经营目的来看生产方式必定是符合实际的，生产方案必定追求合理性，因此我们对于每个加工窖中的加工原料种类限制在 1 到 4 之间。原料种类大于 4 种的不予考虑，这就极大的简化了问题的复杂程度，并且该简化是合理的，符合企业实际生产的。同时要求混合方案达到质量最高的同时，还必须使投放的混合原料的重量在加工窖的加工重量范围上限和下限之间。我们从 9 个加工窖进行着手，通过建立加工原料重量组合系数矩阵，将每个加工窖的质量范围进行约束，从而建立数学模型，进行求解。
  问题 3 的分析
  问题 3 是将 16 个加工原料进行混合全部放入 9 个加工窖中，求出平均效能率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率。显然问题三同问题二一样属于最优问题，并在约束条件之下寻找加工原料的最优混合方案。问题中包含 16 种元素，9 个加工窖。假设在加工原料混合方案确定后，将混合原料投放到 9 个加工窖形成 9 个加工包。则每一个加工包都有一个效能率。通过对 16 种加工原料相关数据的分析，不难发现，由于加工窖自身没有加工效率问题，我们默认加工窖的加工效率是 1，对于每个加工包的效能率无影响。同时每种加工原料的能效率是定值，且不会随着外界条件发生改变。因此，影响单个加工包效能率的因素为每个加工窖中的每种加工原料的质量分配。在明确影响因素的前提条件下，建立起优化目标函数，在问题 2 的基础之上结合题目三所给的约束条件进行求解。利用蒙特卡洛算法进行优化，获得最优解，给出方案配比完成附表 3。
  问题 4 的分析
  问题 4 要求在允许部分加工窖不生产的情况下，满足给定的两个条件，一个是成本尽量低，另一个是平均效能率超过 80%的加工包尽量多，进而完成加工任务，即取消一次性加工的限制，可以多次加工。从本质上来说，问题 4 属于双目标优化问题，即在各种约束条件下设计出一个可以使得成本最小化、平均效能率超过 80%的加工包尽量多的混合方案。我们采用线性加权和法进行双目标优化。该问题的难点在于同时从成本以及效能率两个角度进行考虑，将复杂的任务预定规则转化为约束条件。在考虑加工成本最低时，我们发现加工窖的容量越大，加工成本越低，因此优先使用加工容量较大的加工窖进行加工。我们按照加工要求，设定约束条件，求解双目标优化模型。
  问题 5 的分析
  问题5的建模与求解过程是综合考虑前4个问题的求解结果进行优化计算的，问题 5 共有 3 个目标函数，属于多目标函数优化问题。由于这 3 个目标函数的最优解已经得到，因此我们直接采用线性加权和法进行求解，建立目标函数。假设饲料质量、加工成本和效能率对工厂加工的重要性相等，我们分别赋予每个指标各三分之一的权系数，以问题 2、问题 3 和问题 4 求解的最优值作为基准，建立新的目标函数进行优化。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

[num,jy,raw]=xlsread('temp.xlsx');
qyz=zeros(120,3);
count=0;
for i=1:15
 for m=i+1:16
 count=count+1;
 qyz(count,1)=num(i,1);
 qyz(count,2)=num(m,1);
 for j=1:10
 jdg=strcmp(jy(i,j),jy(m,j));
 if jdg
 qyz(count,3)=qyz(count,3)+1;
 end
 end
 end
end
temp=find(qyz(:,3));
yxqyz=qyz(temp,:);
qyzpj=mean(qyz(:,3));
stdqyz=std(qyz(:,3));
count=1;
num2=nan.*ones(16);
for i=1:size(qyz,1)
 num2(qyz(i,1),qyz(i,2))=qyz(i,3);
 num2(qyz(i,2),qyz(i,1))=qyz(i,3);
 num2(qyz(i,1),qyz(i,1))=10;
end
num2(16,16)=10;
for i=1:14
 for j=i+1:15
 for k=j+1:16
 if num2(i,j)*num2(i,k)*num2(j,k)~=0
 qy3z(count,1:3)=[i,j,k];
 qy3z(count,4)=(num2(i,j)+num2(i,k)+num2(j,k))/3;
 qy3z(count,5)=num(i,2)+num(j,2)+num(k,2);
 count=count+1;
 end
 end
 end
end
ttt=find(qy3z(:,5)>1200);
qy3z(ttt,:)=[];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function [ xxx ] = creatxbq()
%UNTITLED13 Summary of this function goes here
% Detailed explanation goes here
try
 load qyz
 load luzi
 load slzl
 alphab=1:16;
 syu=ones(1,16);
 xxx=zeros(9,16);
 qudiao=ceil(4*rand());
 qudiao=qudiao-1;
 if qudiao
 prob=[100 100 100 20 20 20 1 1 1];
 prob=prob/sum(prob);
 luzinm=1:9;
 kd=[];
 while max(size(kd))~=qudiao
 kd1=randsrc(1,qudiao,[luzinm;prob]);
 kd = unique (kd1);
 end
 end 
 for i=9:-1:1
 jdg=find(kd==i);
 if isempty(jdg)==0 &&i~=1
 jdg=[];
 continue
 end 
 if isempty(jdg)==0 && i==1 
 else 
 dq=ones(1,4); 
 temp=1./(abs(syu-ones(1,16)*luzi(1,i))+0.1);
 prob=temp/sum(temp);
 if i==9||i==8||i==7 
 end
 numi1=randsrc(1,1,[alphab;prob]);
 dq(1,1)=numi1;
 if syu(numi1)*slzl(numi1)<luzi(1,i)
 bl1=syu(numi1);
 else
 if syu(numi1)*slzl(numi1)>=500 && numi1~=10
 bl1=500/slzl(numi1);
 else

bl1=luzi(1,i)/slzl(numi1);
 end
 end
 xxx(i,numi1)=bl1;
 mass=xxx(i,:)*slzl;
 syu(numi1)=syu(numi1)-xxx(i,numi1);
 if numi1==10||mass<500
 %xuan2
 else
 if mass>=luzi(1,i) && i~=1
 continue 
 end
 end 
 mass=(xxx(i,:)*slzl);
 qyi1=find(qyz(dq(1,1),:));
 qyi1(find(qyi1==numi1))=[];
 if sum(syu(qyi1))~=0
 prob=syu(qyi1)/sum(syu(qyi1));
 numi2=randsrc(1,1,[qyi1;prob]);
 dq(1,2)=numi2;
 if mass+syu(numi2)*slzl(numi2)<=luzi(1,i)
 bl2=syu(numi2);
 else
 slslsl=luzi(2,i)-(xxx(i,:)*slzl);
 slslmin=luzi(1,i)-xxx(i,:)*slzl;
 if slslmin<0
 slslmin=0;
 end
 
bl2=ceil(100*(slslmin/slzl(numi2)+(50/slzl(numi2))*rand()))/100;
 end
 
 xxx(i,numi2)=bl2;
 
 mass=(xxx(i,:)*slzl);
 syu(numi2)=syu(numi2)-xxx(i,numi2);
 if mass>=luzi(1,i) && mass<=luzi(2,i)&&i~=1
 continue
 
 end
 
 
 
 qyi112=qyi1;
count=0;
 for j=1:size(qyi1,2)
 if qyz(qyi1(j),numi2)~=0
 count=count+1;
 qyi12(count)=qyi112(j);
 end
 end
 qyi12(find(qyi12==numi2))=[];
 if sum(sum(syu(qyi12)))~=0
 
 prob=syu(qyi12)/sum(syu(qyi12));
 
 numi3=randsrc(1,1,[qyi12;prob]);
 mass=(xxx(i,:)*slzl);
 if mass+syu(numi3)*slzl(numi3)<=luzi(2,i)
 bl2=syu(numi3);
 else
 slslsl=luzi(2,i)-(xxx(i,:)*slzl);
 slslmin=luzi(1,i)-xxx(i,:)*slzl;
 if slslmin<0
 slslmin=0;
 end
 bl2=slslmin/slzl(numi3);
 end
 xxx(i,numi3)=bl2;
 syu(numi3)=syu(numi3)-xxx(i,numi3); 
 end
 end
 mass=(xxx(i,:)*slzl);
 if mass<luzi(1,i)
 tttt=find(xxx(i,:));
 for j=1:max(size(find(xxx(i,:))))
 ysl=find(xxx(:,tttt(j)));
 for k=1:max(size(ysl))
 
yslimass=(xxx(ysl(k),:)*slzl-luzi(1,ysl(k)))/slzl(j);
 if xxx(ysl(k),tttt(j))<yslimass
 xxx(i,tttt(j))=xxx(i,tttt(j))+ 
xxx(ysl(k),tttt(j))-1/slzl(j);
 xxx(ysl(k),tttt(j))=1/slzl(j);
 else
 xxx(i,tttt(j))=xxx(i,tttt(j))+yslimass;
xxx(ysl(k),tttt(j))= 
xxx(ysl(k),tttt(j))-yslimass;
end
 end
 end 
 end 
 end 
 if i==1
 jsy=find(syu);
 if jsy
 for j=1:max(size(jsy))
 yyy=find(xxx(:,jsy(j)));
 if yyy
 for k=1:size(yyy)
 if syu(jsy(j))==0
 continue
 end
ksy=luzi(2,yyy(k))-xxx(yyy(k),:)*slzl;
if ksy
 if ksy>syu(jsy(j))*slzl(jsy(j))
 
xxx(yyy(k),jsy(j))=xxx(yyy(k),jsy(j))+syu(jsy(j));
 syu(jsy(j))=0;
 else
 
xxx(yyy(k),jsy(j))=xxx(yyy(k),jsy(j))+ksy/slzl(jsy(j));
 
syu(jsy(j))=syu(jsy(j))-ksy/slzl(jsy(j));
 end 
 end
 end 
 end
 end
 end
 end 
 end
catch
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可