C语言 插入类排序（直接插入排序、折半插入排序、希尔排序）_插入类排序为

前言

插入类排序是指一类基于插入操作的排序算法，包括直接插入排序、折半插入排序、希尔排序等。其基本思想是将待排序序列分为已排序区间和未排序区间两部分，每次从未排序区间中取出一个元素，并在已排序序列中找到正确的位置将其插入进去，这样，类似于扑克牌插入的方式能够保证已排序序列一直是有序的，使得已排序区间不断扩大，最终整个序列有序。

---

直接插入排序

直接插入排序（Straight Insertion Sort）是一种简单直观的排序算法。其基本思路是：将待排序的数据分为已排序区间和未排序区间两部分，每次从未排序区间中取出一个元素，在已排序区间中找到合适位置并插入。

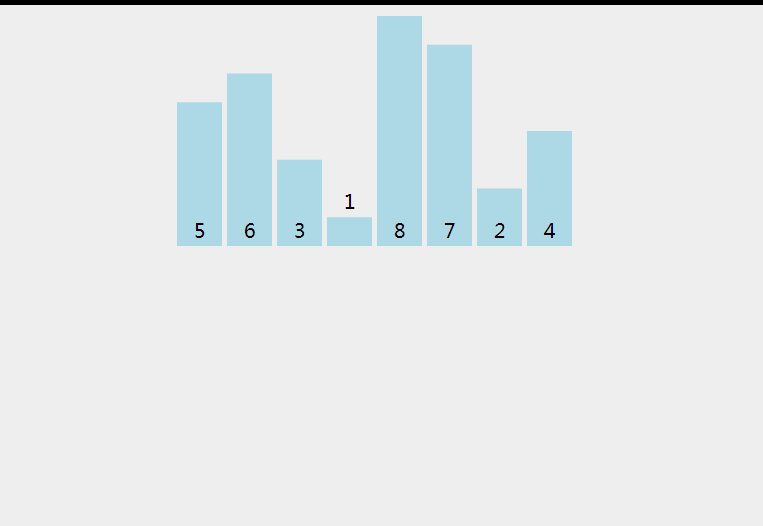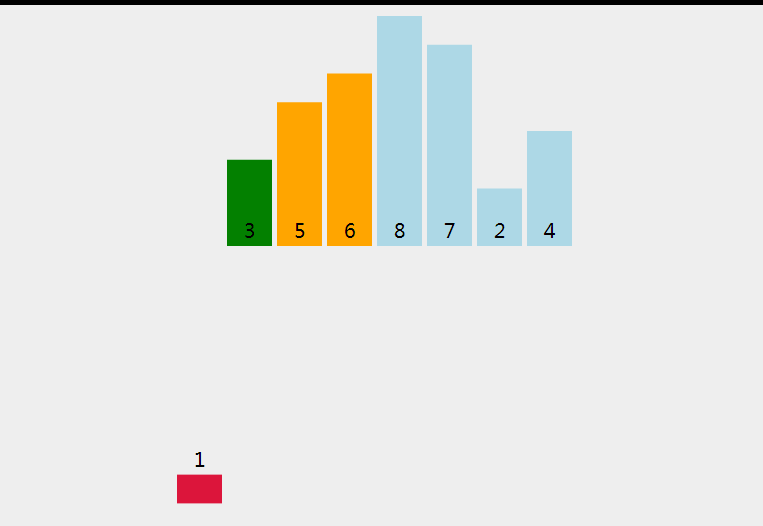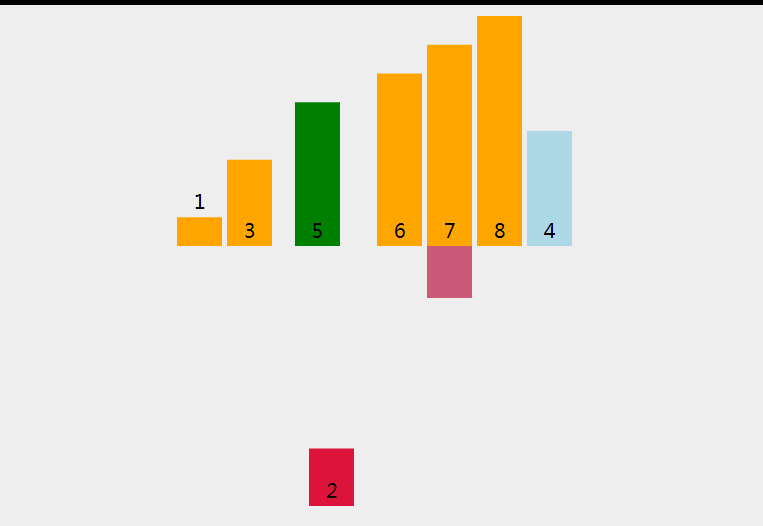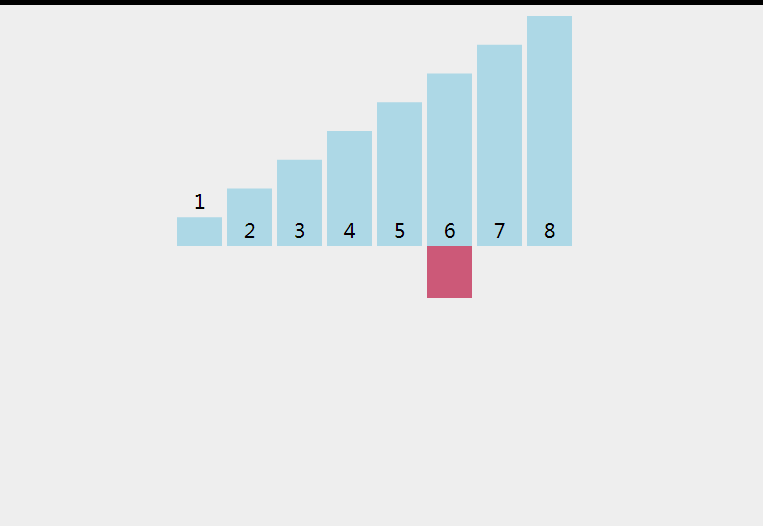
以下是直接插入排序的C语言实现：

//直接插入排序,升序
void InsertSort(int* arr, int arr_size) {
	int i, j, temp;
	for (i = 1; i < arr_size; i++) {
		temp = arr[i];//待排元素arr[i]
		//将比temp大的元素后移
		for (j = i - 1; j >= 0 && arr[j] < temp; j--)
			arr[j + 1] = arr[j];
 
		arr[j + 1] = temp;//将待排元素arr[i]插入正确位置
	}
}

实际上，直接插入排序不是通过交换来完成元素的插入，而是通过不断挪动元素来实现插入操作的。

算法分析

时间复杂度：

• 最好情况下，原始序列已经有序，只需要一次扫描即可，时间复杂度为 O(n)；
• 最坏情况下，原始序列完全逆序，需要进行 n-1 轮比较和移动，每轮比较需遍历整个已排序的序列，因此时间复杂度为 O(n^2)；
• 平均情况下，其时间复杂度为 O(n^2)。

空间复杂度：

直接插入排序是在原数组上进行排序，除了一个变量用于暂存当前待插入的元素外，并不需要额外占用空间，因此其空间复杂度为 O(1)。

---

折半插入排序

折半插入排序（Binary Insertion Sort）是在直接插入排序的基础上进行了改进。其思想是：将待排序序列分为已排序区间和未排序区间两部分，每次从未排序区间中取出一个元素，利用二分查找法在已排序区间中找到插入位置并插入。

以下是折半插入排序的C语言实现：

//折半插入排序,升序
void BInsertSort(int* arr, int arr_size) {
	int i, j, temp, left, right, mid;
	for (i = 1; i < arr_size; i++) {
		temp = arr[i];//待排元素arr[i]
		//折半查找插入位置
		left = 0, right = i - 1;
		while (left <= right) {
			mid = (left + right) / 2;
			if (arr[mid] < temp)
				right = mid - 1;
			else
				left = mid + 1;
		}
		//将大于等于temp元素后移一位
		for (j = i - 1; j >= left; j--)
			arr[j + 1] = arr[j];
		arr[left] = temp;//将待排元素arr[i]插入正确位置
	}
}

 算法分析

 时间复杂度：

在查找位置时，利用折半查找法可以将查找元素的比较次数降至 logn，而插入新元素的平均移动距离约为 n/4，因此时间复杂度为 O(nlogn)，比直接插入排序要快得多。
空间复杂度：

与直接插入排序相同，折半插入排序空间使用的是原数组，所以它的空间复杂度为 O(1)。

---

希尔排序

希尔排序（Shell Sort）是一种插入排序算法的改进版本，通过将待排序列划分为多个子序列来实现更高效的排序。其关键在于定义一个增量序列，用这个增量序列将待排序元素分成若干组，对每组数据进行直接插入排序，然后逐步减小增量，继续进行排序操作，直到增量为1时完成最后一次排序。

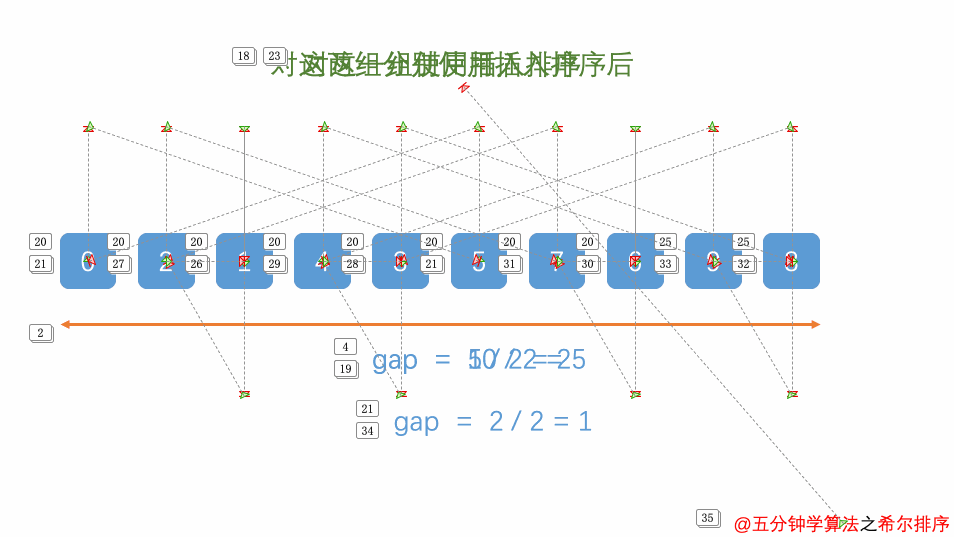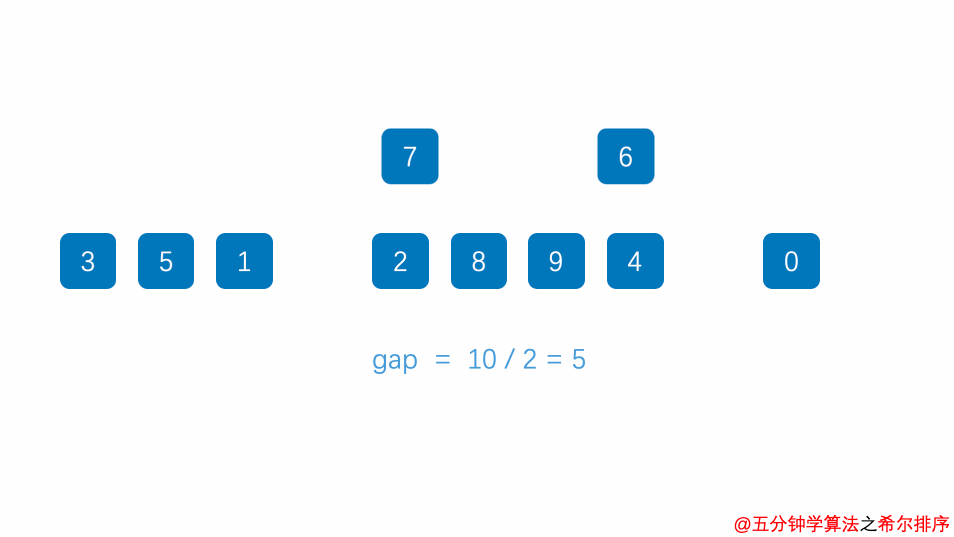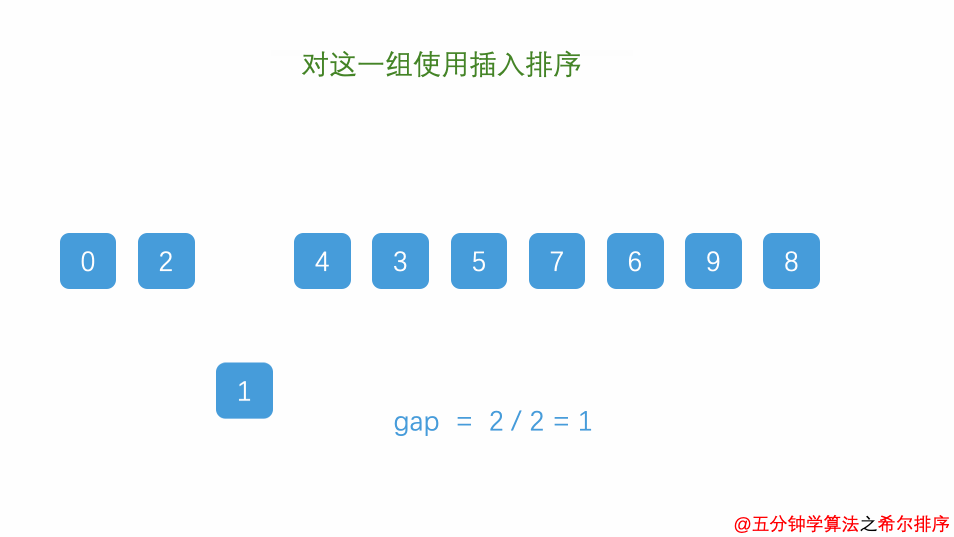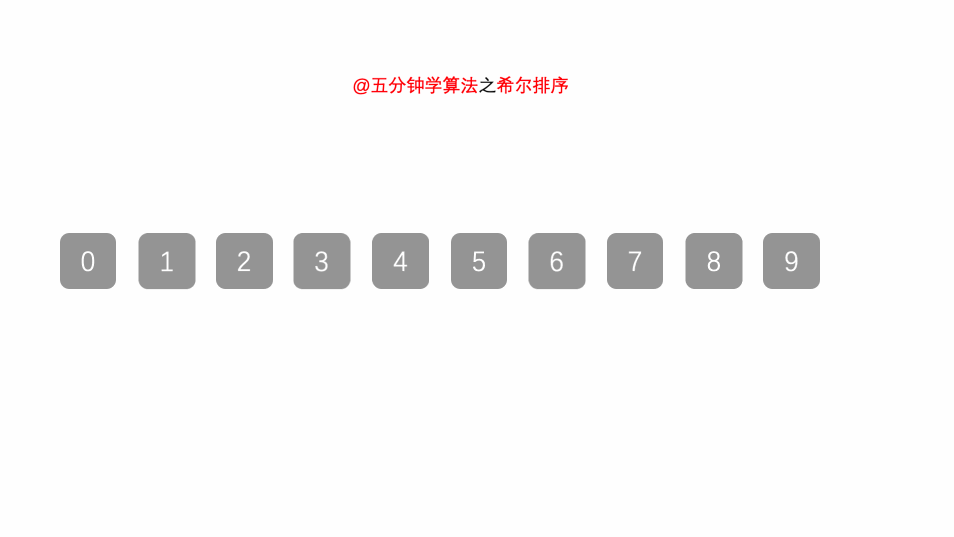
基本流程：

1. 首先定义增量序列，通过gap/2不断缩小增量，直到增量gap等于1为止。在每一轮中，gap表示当前所使用的步长（间隔）。
2. 对于每个增量gap，将待排序序列分成若干个子序列，从第gap个元素开始以gap为增量选取元素，在该子序列中进行插入排序。
3. 缩小增量gap，重新分组，继续对所有子序列进行插入排序操作。
4. 当增量gap=1时，进行最后一次排序，整个数组就变成了一个有序序列，排序完成。

以下是希尔排序的C语言实现：

//希尔排序,升序
void ShellSort(int* arr, int arr_size) {
	int i, j, gap, temp;
	//定义增量序列
	for (gap = arr_size / 2; gap > 0; gap /= 2) {
		//对每个子序列进行插入排序
		for (i = gap; i < arr_size; i++) {
			temp = arr[i];
			for (j = i - gap; j >= 0 && arr[j] < temp; j -= gap)
				arr[j + gap] = arr[j];
			arr[j + gap] = temp;
		}
	}
}

当增量d=1时，与直接插入排序无异，那为什么一般情况下希尔排序效率会更高呢？

这是因为，直接插入排序在面对较大数量的无序数据时，需要不断地进行元素的比较和移动，导致时间复杂度较高。

而希尔排序通过修改插入排序过程中的增量（即步长）来解决这一问题。它将待排序的数组按照一定的间隔分割成多个子序列，然后再对每个子序列进行插入排序。在排序结束之后，缩小间隔并重复上述操作，最终使整个序列有序。

由于使用了增量，希尔排序在处理相同数据量的情况下，能够以更快的速度跨越大量的元素，从而减少了比较和交换的次数，在效率上比直接插入排序快许多。

算法分析

时间复杂度：

希尔排序的时间复杂度取决于步长的选择方式，最差情况下为 O(n^2)，但是对于其他一些步长序列，其时间复杂度可以达到 O(nlogn)。
空间复杂度： 

希尔排序不需要额外的辅助空间，所以空间复杂度是 O(1)。

---

总结

总体来说，插入类排序的时间复杂度都无法达到线性对数级别以下，但是它们具有实现简单、稳定性好等优点，在一些特定场景下还是被广泛使用的。同时，它们的空间复杂度虽然不同，但均在常数级别，因此很适合内存较小的设备上执行排序操作。