- 1【华为OD】手撕代码:求大写英文字母的字符串S所有不相同排列数 python代码实现[思路+代码]_华为od手撕代码python
- 2适合android手机 pdf阅读器,手机版pdf阅读器有哪些 这五款软件一定有适合你的
- 3大数据导论(四:大数据的存储)_大数据存储
- 4 Vert.x Blueprint 系列教程(三) | Micro-Shop 微服务应用实战
- 5Python 实战 | 文本分析之文本关键词提取_python中文自然语言处理基础与实践自动提取文本关键词编程实现
- 6Fiddler如何抓取手机APP数据包_fiddler抓手机的包
- 7软件测评师之报考大纲(一)
- 8使用redis进行短信登录验证(验证码打印在控制台)_如何利用redis去实现短信验证码登录-6位随机数,90s有效,一个手机号1个小时内只能
- 9java多线程——线程池源码分析(一)
- 10【项目管理】原则之六--展现领导力行为_项目 展现领导力原则
排序——插入排序(直接插入排序、希尔排序、折半插入排序)_排序算法直接插入排序和折半插入排序
赞
踩
排序这个文章我本来想写一篇的,但是想了想太长了,最后我还是决定拆开来写吧。第一部分主要是讲插入排序的,包括直接插入排序和希尔排序。
直接插入排序(straight insertion sort)
直接插入排序算法简单、容易实现,当序列中的记录基本有序或待排序记录较少时,是最佳的排序方法。基本思想是依次将待排序序列中的每一个记录插入到一个已排好序的序列中,直到全部记录都排好序。可以想一下打扑克的时候,每抓到一张牌就会插入到你手中已经按顺序理好的牌中。
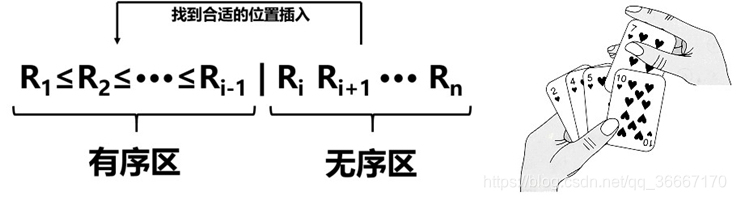
- 将整个待排序的记录划分为有序区和无序区,初始时有序区为待排序记录序列中的第一个记录,无序区包括所有的剩余待排序记录
- 讲无序区第一个记录插入到有序区的合适位置中,从而使无序区减少一个记录,有序区增加一个记录
- 重复2直到无序区中没有记录为止。
例如待排序序列序列12 15 9 20 6 31 24
| 初试键值序列 | [ 12 ] 15 9 20 6 31 24 |
|---|---|
| 第一趟 | [ 12 15 ] 9 20 6 31 24 |
| 第二趟 | [ 9 12 15 ] 20 6 31 24 |
| 第三趟 | [ 9 12 15 20 ] 6 31 24 |
| 第四趟 | [ 6 9 12 15 20 ] 31 24 |
| 第五趟 | [ 6 9 12 15 20 31 ] 24 |
| 第六趟 | [ 6 9 12 15 20 24 31 ] |
代码
a为待排序数组,数组长度n,但是注意此时是将数组a的第一个位置,即a[0]作为哨兵,暂存你从无序区选到的数。因此你实际排序的数只有n-1个。
void InsertSort(int r[],int n)
{
int i,j;
for(i=2;i<n;i++) //0号单元作为哨兵,1号已经是有序区
{
r[0]=r[i]; //暂存关键码
for(j=i-1;r[0]<=r[j];j--) //r[0]<r[j]也可
r[j+1]=r[j];
r[j+1]=r[0];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
算法分析
| / | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 最好情况 | O ( n ) O(n) O(n) | |
| 最坏情况 | O ( n 2 ) O(n^2) O(n2) | |
| 平均 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1 ) O(1) |
实例
待排序序列12,46,75,46,1,35,64 共七个数,因此需要设置一个容量为8的数组。

你只看r[1]到r[7]就行了,不用关注哨兵r[0]等于几,因为他只是一个暂存位置,可能存的是你无序区的第一个数,也可能是存的你有序区的倒数第二个数。

完整代码:
#include<iostream> using namespace std; void print1(int r[],int n) //过程输出 { cout<<"r["<<0<<"] = "<<r[0]<<" 哨兵"<<endl; for(int i=1;i<n;i++) cout<<"r["<<i<<"] = "<<r[i]<<endl; } void print2(int r[],int n) //常规输出 { for(int i=1;i<n;i++) cout<<"r["<<i<<"] = "<<r[i]<<endl; } void InsertSort(int r[],int n) { int i,j; for(i=2;i<n;i++) //0号单元作为哨兵 { r[0]=r[i]; //暂存关键码 for(j=i-1;r[0]<=r[j];j--) r[j+1]=r[j]; r[j+1]=r[0]; cout<<"第"<<i-1<<"趟结果"<<endl; print1(r,8); cout<<endl; } } int main() { int r[8]={0,12,46,75,46,1,35,64}; cout<<"待排序数组:"<<endl; print2(r,8); cout<<endl; InsertSort(r,8); cout<<"排序后数组:"<<endl; print2(r,8); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
折半插入排序
这个就不多说了,就是把直接插入排序中在有序区进行顺序查找替换为二分查找。
代码
void BInsertSort(int a[],int n) { int i,j,low,high,mid; for (i=2;i<n;i++) { a[0]=a[i]; low=1; high=i-1; while(low<=high) { mid=(low+high)/2; if (a[mid]>a[0]) high=mid-1; else low=mid+1; } for(j=i-1;j>=high+1;j--) a[j+1]=a[j]; a[high+1]=a[0]; //a[low]=a[0]; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
希尔排序(shell sort)
希尔排序又称缩小增量排序,是对直接插入排序的一种改进。基本思想是将待排序序列分成若干子序列,在子序列内进行插入排序,待整个序列基本有序时,对全体记录进行一次插入排序。
排序过程
假设待排序的记录为n个,先取整数
d
<
n
d<n
d<n,将所有相距为d的记录构成一组,从而将整个待排序记录序列分割成为d个子序列,对每个子序列分别进行直接插入排序,然后再缩小间隔d。重复上述分割,再对每个子序列分别进行直接插入排序,直到最后取d=1,即将所有记录放在一组进行一次直接插入排序,最终将所有记录重新排列成按关键码有序的序列。d的取值可以自己决定,一般来说,按照希尔最早提出的方法是
d
1
=
⌊
n
/
2
⌋
d_1=\lfloor n/2 \rfloor
d1=⌊n/2⌋,
d
i
+
1
=
⌊
d
i
/
2
⌋
d_{i+1}=\lfloor d_i/2 \rfloor
di+1=⌊di/2⌋,最后增量为1。
例如:待排序徐序列59,20,17,36,98,23,14,13,28
| shell sort | d | 序列 |
|---|---|---|
| 第一趟 | 9 / 2 = 4 9/2=4 9/2=4 | 28 59 98 20 23 14 17 13 36 结果:28 20 14 13 59 23 17 36 98 |
| 第二趟 | 4 / 2 = 2 4/2=2 4/2=2 | 14 17 28 59 98 19 20 23 36 结果:14 19 17 20 28 23 59 36 98 |
| 第三趟 | 2 / 2 = 1 2/2=1 2/2=1 | (即直接插入排序) 结果:14 17 19 20 23 28 36 59 98 |
代码
希尔排序中a为待排序数组,其中有n个空间,注意此时是将数组a的第一个位置,即a[0]作为暂存单元,不是哨兵。因此你实际排序的数只有n-1个。
void ShellSort(int a[],int n)
{
int d,i,j;
for(d=n/2;d>=1;d/=2) //设置增量
{
for (i=d+1;i<n;i++)
{
a[0]=a[i];
for (j=i-d;j>0&&a[0]<a[j];j=j-d)
a[j+d]=a[j];
a[j+d]=a[0];
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
算法分析
| / | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 最好情况 | / | |
| 最坏情况 | O ( n 2 ) O(n^2) O(n2) | |
| 平均 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( ) O( ) O() |
希尔排序的增量取法有各种方案。按照希尔提出的方法是
d
1
=
⌊
n
/
2
⌋
d_1=\lfloor n/2 \rfloor
d1=⌊n/2⌋,
d
i
+
1
=
⌊
d
i
/
2
⌋
d_{i+1}=\lfloor d_i/2 \rfloor
di+1=⌊di/2⌋,最后增量为1。但由于直到最后一步,在奇数位置的元素才会与偶数位置的元素进行比较,这样使用这个序列的效率将很低。后人又提出各种效率更高的增量取法。不同增量取值方法会使希尔排序算法的性能有很大差异。 因此对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算排序码的比较次数和元素移动次数,但想要弄清排序码比较次数和元素移动次数与增量选择之间的依赖关系,并给出完整的数学分析,还没有人能够做到。在 Knuth所著的《计算机程序设计技巧》第3卷中,利用大量的实验统计资料得出,当n很大时,排序码平均比较次数和元素平均移动次数大约在
n
1.25
n^{1.25}
n1.25到
1.6
n
1.25
1.6n^{1.25}
1.6n1.25的范围内。 我觉得就是现在大部分教材中的
O
(
n
1.3
)
O(n^{1.3})
O(n1.3)。
我还翻译了一个文章,感兴趣的可以看看,里面汇总了一些文献对于希尔排序的性能推算。希尔排序复杂度详细分析(翻译来源:Hans Werner Lang教授)
实例
待排序序列59,20,17,36,98,23,14,13,28 共9个数,因此需要设置一个容量为10的数组。

#include<iostream> using namespace std; void print(int r[],int n) //常规输出 { for(int i=1;i<n;i++) cout<<"r["<<i<<"] = "<<r[i]<<endl; cout<<endl; } void ShellSort(int a[],int n) { int d,i,j; int count=1; //用于过程输出,可删除 for(d=n/2;d>=1;d/=2) { for (i=d+1;i<n;i++) { a[0]=a[i]; for (j=i-d;j>0&&a[0]<a[j];j=j-d) a[j+d]=a[j]; a[j+d]=a[0]; } /*-----过程输出可删除--------*/ cout<<"第"<<count<<"趟"<<endl; cout<<"d = "<<d<<endl; count++; print(a,n); /*-----过程输出--------*/ } } int main() { int a[10]={0,59,20,17,36,98,23,14,13,28}; cout<<"待排序数组"<<endl; print(a,10); ShellSort(a,10); cout<<"排序结果"<<endl; print(a,10); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41



