深度学习速成版02---卷积神经网络_卷积神经网络隐藏层

线性神经网络局限性

任意多个隐层的神经网络和单层的神经网络都没有区别，而且都是线性的，而且线性模型的能够解决的问题也是有限的

神经网络的种类

• 基础神经网络：线性神经网络，BP神经网络，Hopfield神经网络等
• 进阶神经网络：玻尔兹曼机，受限玻尔兹曼机，递归神经网络等
• 深度神经网络：深度置信网络，卷积神经网络，循环神经网络，LSTM网络等

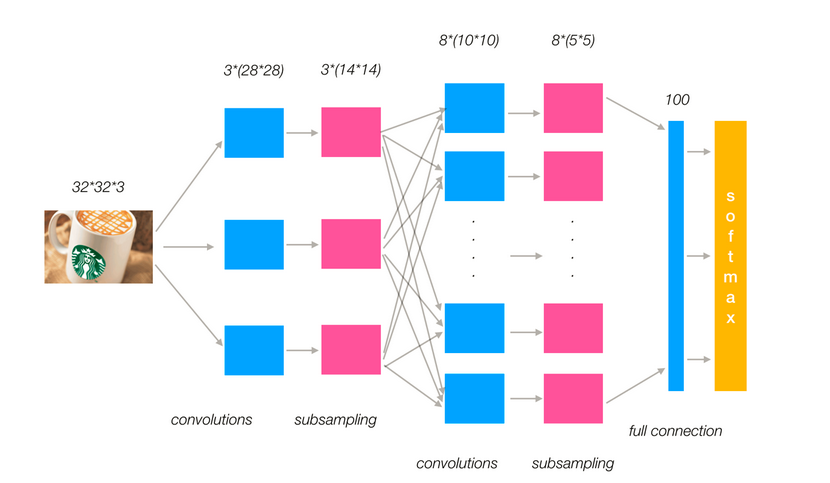
卷积神经网络

传统意义上的多层神经网络是只有输入层、隐藏层、输出层。其中隐藏层的层数根据需要而定，没有明确的理论推导来说明到底多少层合适卷积神经网络CNN，在原来多层神经网络的基础上，加入了更加有效的特征学习部分，具体操作就是在原来的全连接的层前面加入了部分连接的卷积层与池化层。卷积神经网络出现，使得神经网络层数得以加深，深度学习才能实现, 通常所说的深度学习，一般指的是这些CNN等新的结构以及一些新的方法（比如新的激活函数Relu等），解决了传统多层神经网络的一些难以解决的问题
卷积神经网络三个结构

神经网络(neural networks)的基本组成包括输入层、隐藏层、输出层。而卷积神经网络的特点在于隐藏层分为卷积层和池化层(pooling layer，又叫下采样层)以及激活层。每一层的作用

• 卷积层：通过在原始图像上平移来提取特征
• 激活层：增加非线性分割能力
• 池化层：通过特征后稀疏参数来减少学习的参数，降低网络的复杂度，（最大池化和平均池化）

为了能够达到分类效果，还会有一个全连接层(FC)也就是最后的输出层，进行损失计算分类。
卷积层

卷积层（Convolutional layer）

卷积神经网络中每层卷积层由若干卷积单元(卷积核)组成，每个卷积单元的参数都是通过反向传播算法最佳化得到的。

卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

卷积核(Filter)的四大要素

• 卷积核个数
• 卷积核大小
• 卷积核步长
• 卷积核零填充大小

接下来我们通过计算案例讲解，假设图片是黑白图片（只有一个通道），一张像素值表

卷积如何计算-大小

卷积核我们可以理解为一个观察的人，带着若干权重和一个偏置去观察，进行特征加权运算。

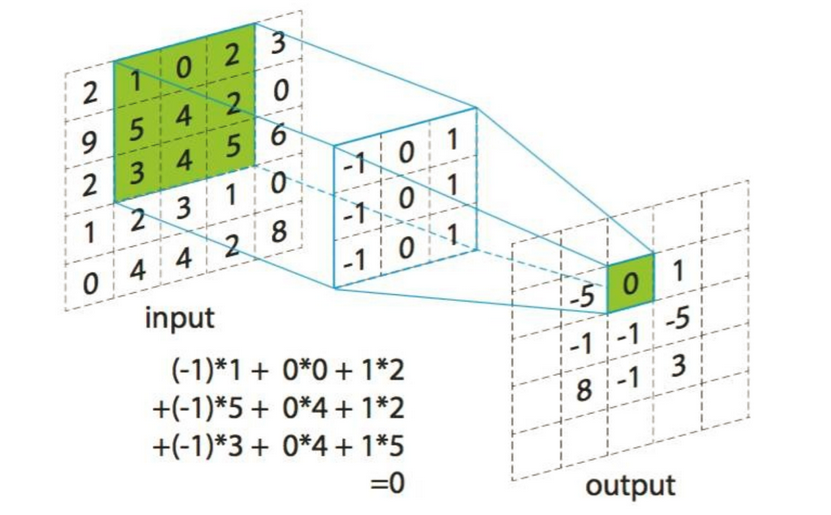
：上述要加上偏置

卷积核大小
    1*1、3*3、5*5
1
2

通常卷积核大小选择这些大小，是经过研究人员证明比较好的效果。这个人观察之后会得到一个运算结果，

那么这个人想观察所有这张图的像素怎么办？那就需要这样

卷积如何计算-步长

需要去移动卷积核观察这张图片，需要的参数就是步长。
假设移动的步长为一个像素，那么最终这个人观察的结果以下图为例：
5x5的图片，3x3的卷积大小去一个步长运算得到3x3的大小观察结果

如果移动的步长为2那么结果是这样

5x5的图片，3x3的卷积大小去两个步长运算得到2x2的大小观察结果

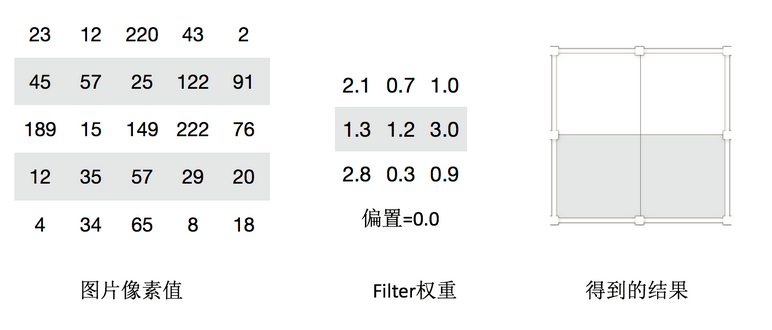
卷积如何计算-卷积核个数

那么如果在某一层结构当中，不止是一个人观察，多个人(卷积核)一起去观察。那就得到多张观察结果。

不同的卷积核带的权重和偏置都不一样，即随机初始化的参数

我们已经得出输出结果的大小有大小和步长决定的，但是只有这些吗，还有一个就是零填充。Filter观察窗口的大小和移动步长会导致超过图片像素宽度！

卷积如何计算-零填充大小

零填充就是在图片像素外围填充一圈值为0的像素。

有两种方式，SAME和VALID

SAME：越过边缘取样，取样的面积和输入图像的像素宽度一致。
VALID：不越过边缘取样，取样的面积小于输入人的图像的像素宽度。
1
2

输出大小计算公式
最终零填充到底填充多少呢？我们并不需要去关注，接下来我们利用已知的这些条件来去求出输出的大小来看结果

通过一个例子来理解下面的公式

计算案例：

1、假设已知的条件：输入图像32*32*1, 50个Filter，大小为5*5，移动步长为1，零填充大小为1。请求出输出大小？

H2 = (H1 - F + 2P)/S + 1 = (32 - 5 + 2 * 1)/1 + 1 = 30

W2 = (H1 - F + 2P)/S + 1 = (32 -5 + 2 * 1)/1 + 1 = 30

D2 = K = 50

所以输出大小为[30, 30, 50]

2、假设已知的条件：输入图像32*32*1, 50个Filter，大小为3*3，移动步长为1，未知零填充。输出大小32*32？

H2 = (H1 - F + 2P)/S + 1 = (32 - 3 + 2 * P)/1 + 1 = 32

W2 = (H1 - F + 2P)/S + 1 = (32 -3 + 2 * P)/1 + 1 = 32

所以零填充大小为：1*1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

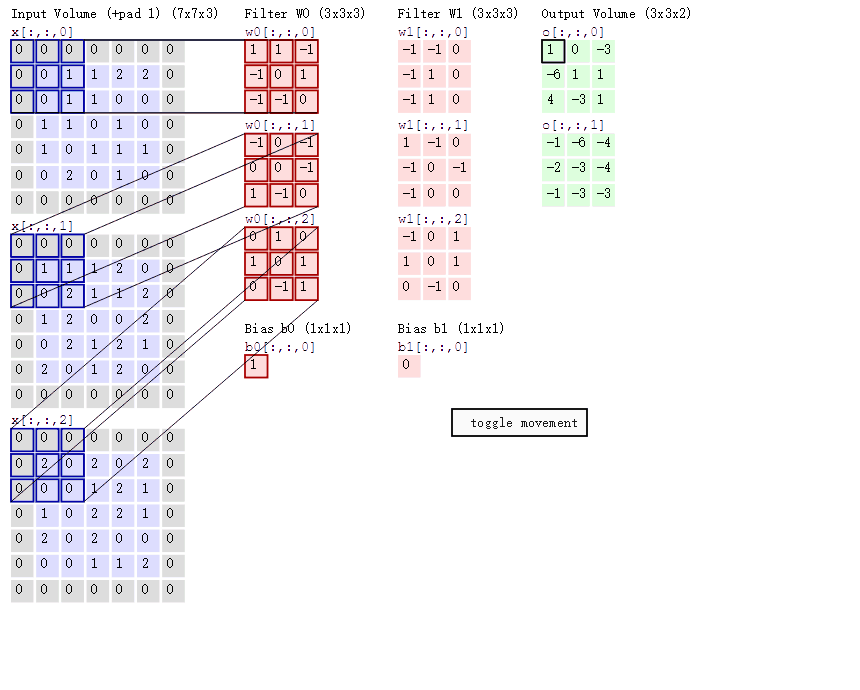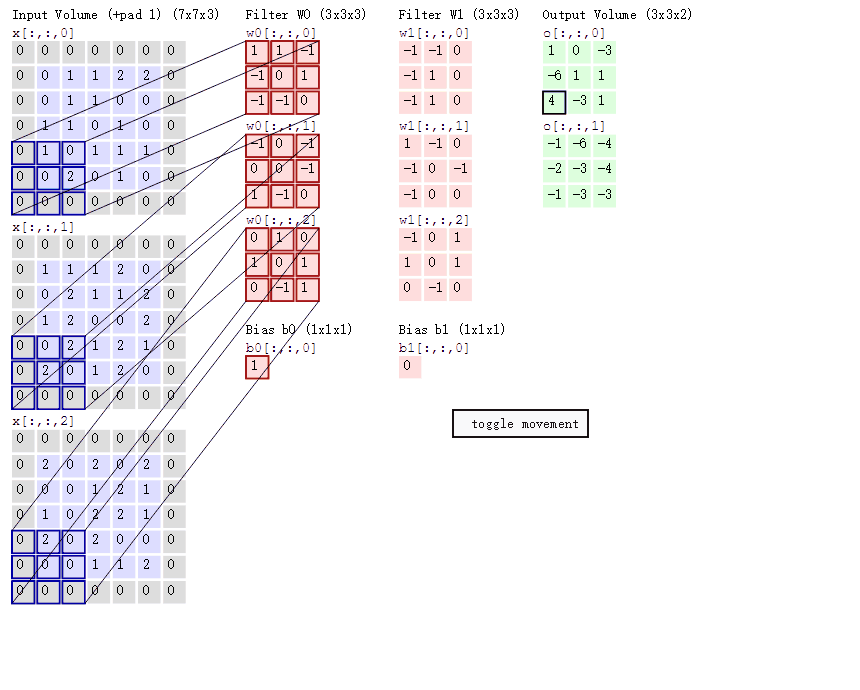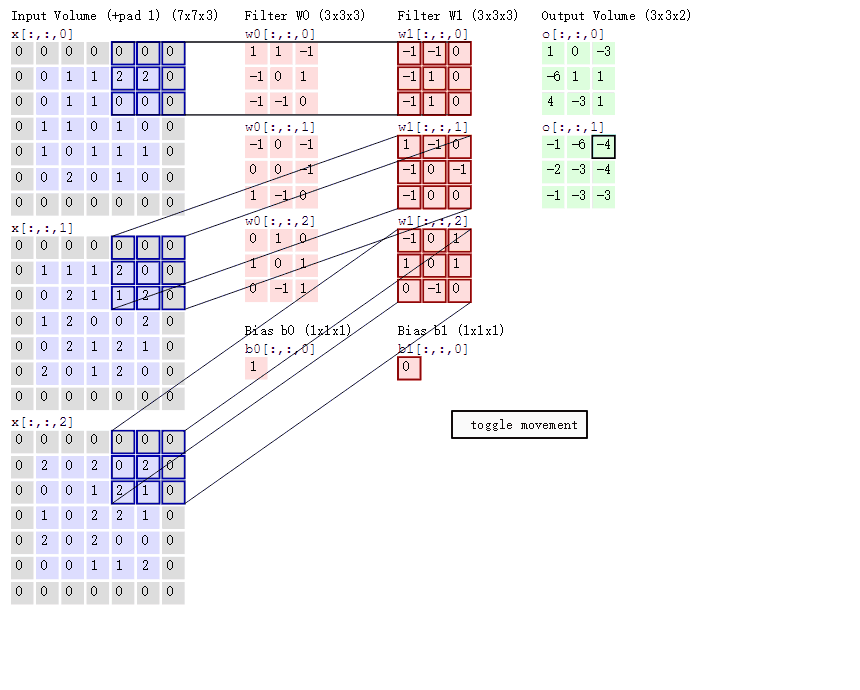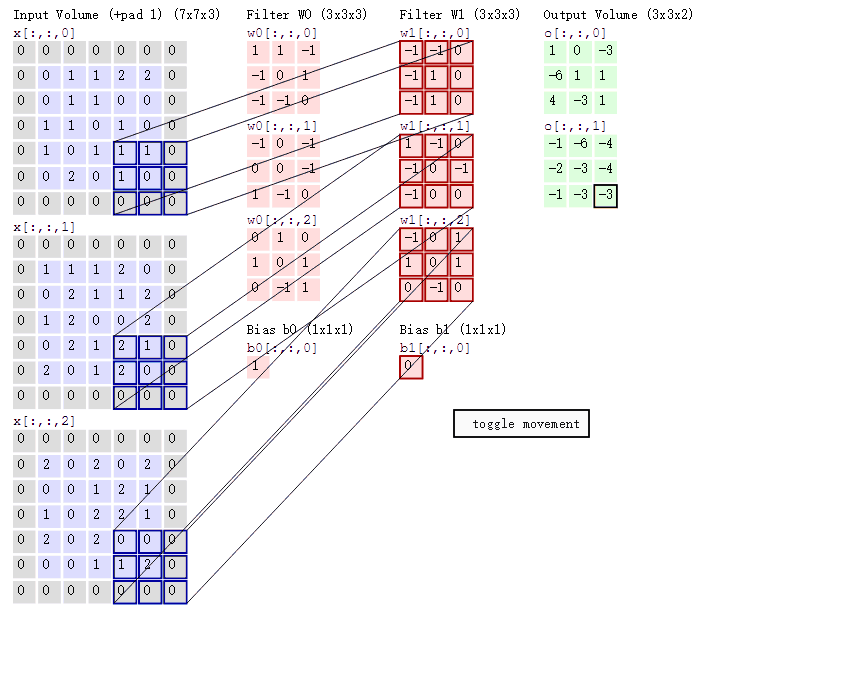
多通道图片如何观察

如果是一张彩色图片，那么就有三种表分别为R，G，B。原本每个人需要带一个3x3或者其他大小的卷积核，现在需要带3张3x3的权重和一个偏置，总共就27个权重。最终每个人还是得出一张结果

激活函数

卷积网络结构采用激活函数，自从网路得到发展之后。大家发现原有的sigmoid这些激活函数并不能达到好的效果，所以采取新的激活函数。

• Relu
  -
  效果是什么样的呢？
  

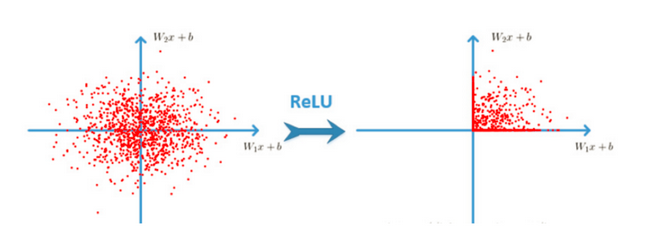
• Relu优点
  有效解决梯度爆炸问题
  计算速度非常快，只需要判断输入是否大于0。SGD(批梯度下降)的求解速度速度远快于sigmoid和tanh

• sigmoid缺点
  采用sigmoid等函数，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。在深层网络中，sigmoid函数 反向传播 时，很容易就会出现梯度梯度爆炸的情况

池化层(Polling)

Pooling层主要的作用是特征提取，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，通常采用最大池化

max_polling:取池化窗口的最大值
avg_polling:取池化窗口的平均值
1
2

池化层计算

池化层也有窗口的大小以及移动步长，那么之后的输出大小怎么计算？计算公式同卷积计算公式一样

计算：224x224x64,窗口为2，步长为2输出结果？

H2 = (224 - 2 + 2*0)/2 +1 = 112

w2 = (224 - 2 + 2*0)/2 +1 = 112
1
2
3
4
5

通常池化层采用 2x2大小、步长为2窗口

BN层

目的：提高网络泛化能力，防止过拟合

BN(Batch Normalization)也属于网络的一层，又称为归一化层。使用BN的好处，包括可以使用更大的学习率,成为CNN的标配

Full Connection层

前面的卷积和池化相当于做特征工程，最后的全连接层在整个卷积神经网络中起到“分类器”的作用。

梯度下降不同优化版本

最朴素的优化算法就是SGD了，梯度下降算法效果也很好，但也存在一些问题选择一个合理的学习速率很难。容易陷入那些次优的局部极值点中

拓展内容（了解）：

    SGD with Momentum

梯度更新规则:Momentum在梯度下降的过程中加入了惯性，使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。

    RMSProp

梯度更新规则:解决Adagrad学习率急剧下降的问题，RMSProp改变了二阶动量计算方法，即用窗口滑动加权平均值计算二阶动量。

    Adam

梯度更新规则:Adam = Adaptive + Momentum，顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量
1
2
3
4
5
6
7
8
9
10
11
12
13

卷积神经网络发展历史

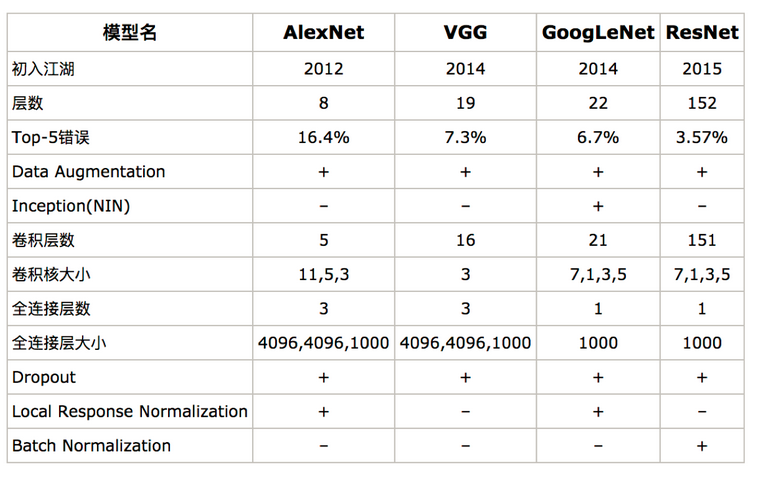
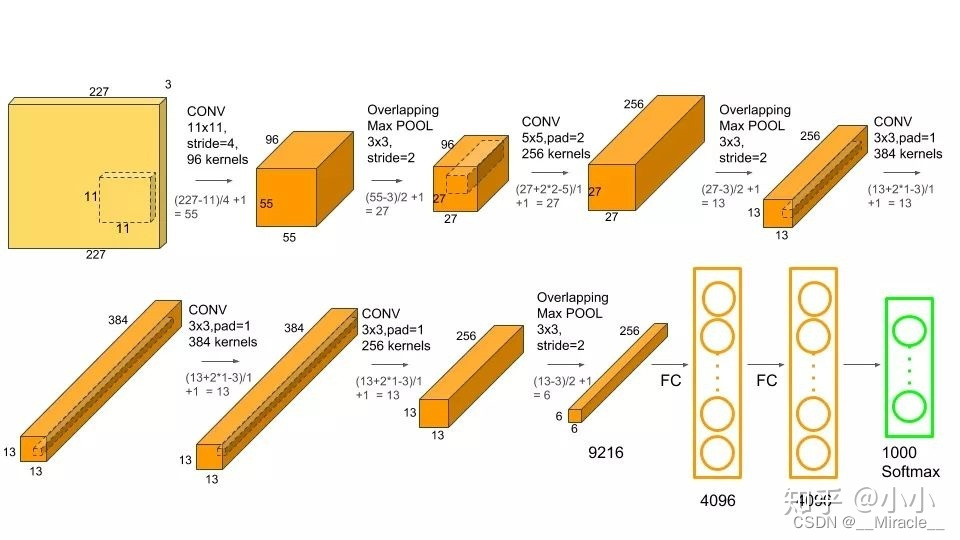
卷积网络其它用途

图像目标检测
    Yolo：GoogleNet+ bounding boxes
    SSD：VGG + region proposals
1
2
3

简单CNN的搭建

import torch
import torch.nn as nn
import torch.nn.functional as F

1
2
3
4

class Net(nn.Module):
    def __init__(self): #定义神经网络结构, 输入数据 1x32x32
        super(Net, self).__init__()
        # 第一层（卷积层）
        self.conv1 = nn.Conv2d(1,6,3) #输入频道1， 输出频道6， 卷积3x3
        # 第二层（卷积层）
        self.conv2 = nn.Conv2d(6,16,3) #输入频道6， 输出频道16， 卷积3x3
        # 第三层（全连接层）
        self.fc1 = nn.Linear(16*28*28, 512) #输入维度16x28x28=12544，输出维度 512
        # 第四层（全连接层）
        self.fc2 = nn.Linear(512, 64) #输入维度512， 输出维度64
        # 第五层（全连接层）
        self.fc3 = nn.Linear(64, 2) #输入维度64， 输出维度2
    
    def forward(self, x): #定义数据流向
        x = self.conv1(x)
        x = F.relu(x)
        
        x = self.conv2(x)
        x = F.relu(x)
        
        x = x.view(-1, 16*28*28)
        x = self.fc1(x)
        x = F.relu(x)
        
        x = self.fc2(x)
        x = F.relu(x)
        
        x = self.fc3(x)
        
        return x
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

net = Net()
print(net)
1
2

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=12544, out_features=512, bias=True)
  (fc2): Linear(in_features=512, out_features=64, bias=True)
  (fc3): Linear(in_features=64, out_features=2, bias=True)
)
1
2
3
4
5
6
7

#生成随机输入
input_data = torch.randn(1,1,32,32) 
print(input_data)
print(input_data.size())
1
2
3
4

tensor([[[[ 0.3055, -0.8828,  0.1044,  ..., -0.4833,  1.1879, -0.0727],
          [ 0.2718, -1.5784, -1.0362,  ..., -0.5160,  0.4685, -0.5401],
          [ 2.4876,  0.1718,  1.2377,  ..., -0.6047, -0.7236,  0.3888],
          ...,
          [-0.8249, -0.3313, -0.3513,  ...,  0.2470, -0.6509, -0.9969],
          [ 1.0528,  0.0348,  0.6416,  ..., -0.4129, -0.1997,  0.1648],
          [ 1.5184,  0.0120, -2.3959,  ..., -1.3124, -0.4289, -0.2882]]]])
torch.Size([1, 1, 32, 32])
1
2
3
4
5
6
7
8

# 运行神经网络
out = net(input_data)
print(out)
print(out.size())
1
2
3
4

tensor([[-0.0375, -0.0235]], grad_fn=<AddmmBackward>)
torch.Size([1, 2])
1
2

# 随机生成真实值
target = torch.randn(2)
target = target.view(1,-1)
print(target)
1
2
3
4

tensor([[-2.1838, -0.4858]])
1

criterion = nn.L1Loss() # 定义损失函数
loss = criterion(out, target) # 计算损失
print(loss)
1
2
3

tensor(1.3043, grad_fn=<L1LossBackward>)
1

# 反向传递
net.zero_grad() #清零梯度
loss.backward() #自动计算梯度、反向传递

1
2
3
4

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.01)
optimizer.step()
1
2
3
4

out = net(input_data)
print(out)
print(out.size())
1
2
3

tensor([[-0.0946, -0.0601]], grad_fn=<AddmmBackward>)
torch.Size([1, 2])
1
2

• 第二次是权值更新损失要比第一次要小一些

criterion = nn.L1Loss() # 定义损失函数  MAE
loss = criterion(out, target) # 计算损失
print(loss)
1
2
3

tensor(1.2574, grad_fn=<L1LossBackward>)
1

Pytorch + CNN 手写数字识别

• 导包个加载mnist数据集

import torch
import torchvision.datasets as dataset
import torchvision.transforms as transforms
import torch.utils.data as data_utils
#data
train_data = dataset.MNIST(root="mnist",
                           train=True,
                           transform=transforms.ToTensor(),
                           download=True)

test_data = dataset.MNIST(root="mnist",
                           train=False,
                           transform=transforms.ToTensor(),
                           download=False)
#batchsize
train_loader = data_utils.DataLoader(dataset=train_data,
                                     batch_size=64,
                                     shuffle=True)

test_loader = data_utils.DataLoader(dataset=test_data,
                                     batch_size=64,
                                     shuffle=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

• 构建CNN

class CNN(torch.nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv =torch.nn.Sequential(
            torch.nn.Conv2d(1, 32, kernel_size=5, padding=2),
            torch.nn.BatchNorm2d(32),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(2)
        )
        self.fc = torch.nn.Linear(14 * 14 * 32, 10)
    def forward(self, x):
        out = self.conv(x)
        out = out.view(out.size()[0], -1)
        out = self.fc(out)
        return out
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 加载模型测试

class CNN(torch.nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv =torch.nn.Sequential(
            torch.nn.Conv2d(1, 32, kernel_size=5, padding=2),
            torch.nn.BatchNorm2d(32),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(2)
        )
        self.fc = torch.nn.Linear(14 * 14 * 32, 10)
    def forward(self, x):
        out = self.conv(x)
        out = out.view(out.size()[0], -1)
        out = self.fc(out)
        return out
cnn = CNN()
# cnn = cnn.cuda()
#loss

loss_func = torch.nn.CrossEntropyLoss()

#optimizer

optimizer = torch.optim.Adam(cnn.parameters(), lr=0.01)

#training
for epoch in range(10):
    for i, (images, labels) in enumerate(train_loader):
#         images = images.cuda()
#         labels = labels.cuda()
        outputs = cnn(images)
        loss = loss_func(outputs, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    print("epoch is {}, ite is "
          "{}/{}, loss is {}".format(epoch+1, i,
                                     len(train_data) // 64,
                                     loss.item()))
    #eval/test
    loss_test = 0
    accuracy = 0
    for i, (images, labels) in enumerate(test_loader):
#         images = images.cuda()
#         labels = labels.cuda()
        outputs = cnn(images)
        #[batchsize]
        #outputs = batchsize * cls_num
        loss_test += loss_func(outputs, labels)
        _, pred = outputs.max(1)
        accuracy += (pred == labels).sum().item()

    accuracy = accuracy / len(test_data)
    loss_test = loss_test / (len(test_data) // 64)

    print("epoch is {}, accuracy is {}, "
          "loss test is {}".format(epoch + 1,
                                   accuracy,
                                   loss_test.item()))

torch.save(cnn, "mnist_model.pkl")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

cnn = torch.load("mnist_model.pkl")
# cnn = cnn.cuda()
#loss
#eval/test
loss_test = 0
accuracy = 0

import cv2
#pip install opencv-python -i http://mirrors.aliyun.com/pypi/simple/   --trusted-host mirrors.aliyun.com
for i, (images, labels) in enumerate(test_loader):
#     images = images.cuda()
#     labels = labels.cuda()
    outputs = cnn(images)
    _, pred = outputs.max(1)
    accuracy += (pred == labels).sum().item()

    images = images.cpu().numpy()
    labels = labels.cpu().numpy()
    pred = pred.cpu().numpy()
    #batchsize * 1 * 28 * 28

    for idx in range(images.shape[0]):
        im_data = images[idx]
        im_label = labels[idx]
        im_pred = pred[idx]
        im_data = im_data.transpose(1, 2, 0)
accuracy = accuracy / len(test_data)
print(accuracy)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

0.9824

CNN构建Cifar10图像分类器

import torch
import torchvision
import torchvision.transforms as transforms
from tqdm import tqdm
1
2
3
4

# (0.5, 0.5, 0.5), (0.5, 0.5, 0.5)  第一个是rgb的均值, 第二个是rgb三通道的方差  都指定为0.5
# 标准化 归一化
transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
    ]
    )

#训练数据集
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, 
                                       download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=16,
                                         shuffle=True, num_workers=2)

#测试数据集
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                      download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=16,
                                        shuffle=False, num_workers=2)



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

Files already downloaded and verified
Files already downloaded and verified
1
2

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

def imshow(img):
    # 输入数据: torch.tensor [c, h, w]
    img = img / 2+0.5
    nping = img.numpy()
    nping = np.transpose(nping, (1,2,0)) # [h,w,c]
    plt.imshow(nping)
    
dataiter = iter(trainloader) #随机加载一个mini batch
images, labels = dataiter.next()

imshow(torchvision.utils.make_grid(images))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self): #定义神经网络结构, 输入数据 3x32x32
        super(Net, self).__init__()
        # 第一层（卷积层）
        self.conv1 = nn.Conv2d(3,6,3) #输入频道3， 输出频道6， 卷积3x3
        # 第二层（卷积层）
        self.conv2 = nn.Conv2d(6,16,3) #输入频道6， 输出频道16， 卷积3x3
        # 第三层（全连接层）
        self.fc1 = nn.Linear(16*28*28, 512) #输入维度16x28x28=12544，输出维度 512
        # 第四层（全连接层）
        self.fc2 = nn.Linear(512, 64) #输入维度512， 输出维度64
        # 第五层（全连接层）
        self.fc3 = nn.Linear(64, 10) #输入维度64， 输出维度10
    
    def forward(self, x): #定义数据流向
        x = self.conv1(x)
        x = F.relu(x)
        
        x = self.conv2(x)
        x = F.relu(x)
        
        x = x.view(-1, 16*28*28)
        x = self.fc1(x)
        x = F.relu(x)
        
        x = self.fc2(x)
        x = F.relu(x)
        
        x = self.fc3(x)
        
        return x
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

net = Net()
print(net)
1
2

Net(
  (conv1): Conv2d(3, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=12544, out_features=512, bias=True)
  (fc2): Linear(in_features=512, out_features=64, bias=True)
  (fc3): Linear(in_features=64, out_features=10, bias=True)
)
1
2
3
4
5
6
7

import torch.optim as optim

criterion = nn.CrossEntropyLoss()  # 交叉熵损失 # 
optimizer = optim.SGD(net.parameters(), lr=0.0001, momentum=0.9)
#  Momentum 梯度下降法，就是计算了梯度的指数加权平均数，并以此来更新权重，它的运行速度几乎总是快于标准的梯度下降算法。
1
2
3
4
5

train_loss_hist = []
test_loss_hist = []
for epoch in range(2):
    for i, data in enumerate(trainloader):
        images, labels = data        
        outputs = net(images)
        loss = criterion(outputs, labels) # 计算损失
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if i%1000==0:
            print("Epoch: {} step: {} Loss: {}".format(epoch, i, loss.item()))


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Epoch: 0 step: 0 Loss: 2.327638864517212
Epoch: 0 step: 1000 Loss: 2.2910702228546143
Epoch: 0 step: 2000 Loss: 2.303840160369873
Epoch: 0 step: 3000 Loss: 2.252164363861084
Epoch: 1 step: 0 Loss: 2.2408382892608643
Epoch: 1 step: 1000 Loss: 2.0526092052459717
Epoch: 1 step: 2000 Loss: 2.0468878746032715
Epoch: 1 step: 3000 Loss: 2.1996114253997803

train_loss_hist = []
test_loss_hist = []

for epoch in tqdm(range(20)):
    #训练
    net.train()
    running_loss = 0.0
    for i, data in enumerate(trainloader):
        images, labels = data        
        outputs = net(images)
        loss = criterion(outputs, labels) # 计算损失
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        running_loss += loss.item()
        if(i%250 == 0): #每250 mini batch 测试一次
            correct = 0.0
            total = 0.0

            net.eval()
            with torch.no_grad():
                for test_data in testloader:
                    test_images, test_labels = test_data
                    test_outputs = net(test_images)
                    test_loss = criterion(test_outputs, test_labels)

            train_loss_hist.append(running_loss/250)
            test_loss_hist.append(test_loss.item())
            running_loss=0.0


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

100%|██████████| 20/20 [50:48<00:00, 148.08s/it]
1

plt.figure()
plt.plot(temp)
plt.plot(test_loss_hist)
plt.legend(('train loss', 'test loss'))
plt.title('Train/Test Loss')
plt.xlabel('# mini batch *250')
plt.ylabel('Loss')
1
2
3
4
5
6
7

Text(0,0.5,'Loss')
1