- 12018年出生率 京沪津普降 东北垫底_2018年上海孩子出生率
- 2不同版本CUDA和cudnn下载安装并配置环境变量_cuda下载按照
- 3Pygame编程(3)draw模块_pygame中draw
- 4QT 实现放大镜跟随鼠标效果
- 5求职数据分析,项目经验该怎么写
- 62023年十四届蓝桥杯省赛大学B组真题(Java完整版)_说明 给你一个无向图,这个无向图有 n 如果你要连接 x,y,那么需要花费 ax+ay 的成
- 7jenkins部署后的操作将jar传入目标服务器并且运行jar包_jenkins 将jar发送到另一台机器
- 8python 科学计数法_Python编程基础篇>04格式化输出转义及input输入
- 9Flutter和Rust如何优雅的交互_flutter rust
- 10c#游戏辅助脚本教程——变量
KNN算法简单?我竟用3万字没写清楚······_n_samples_fit_
赞
踩
大家好,我是小伍哥,本文非常长,建议先收藏,有空再看
谈起KNN,很多人都会觉得非常简单,甚至会露出不屑+鄙视,包括我自己,当初也是如此,当我进行深入的研究,发现真是大意了。
大家都知道KNN可以用于分类,但是它能不能用于回归?KNN的5个有监督方法你是否都知道?K值怎么确定呢?距离可以加权么?为了取Top K,必须要对距离全部排序吗?基于质心的KNN你了解么?有没有方法减少KNN的计算复杂度?KNN还可以做图发现?KNN还可以限定邻居半径的有监督?KNN怎么进行异常检测?KNN是否能够找到我想要的邻居?
在万物皆颗Embedding的时代,我们就可以用近邻推推荐Nearest Neighbor(KNN并不低级,Youtube也是用这个,之前还有开源,对视频库中的所有视频根据向量做最近邻算法,得到top-N的视频作为召回结果)可以做到:物物推荐,人人推荐,人物推荐。有了文本的Embedding,我们可以进行文本聚类挖掘·····,可以说这个算法非常非常的丰富,加上代码,30000字,都有很多写的不是很到位,后面我们慢慢挖。
本文涉及两个库:scikit-learn 和 pyod,前者做有监督和距离等计算,后者负责无监督,本文的框架也是依据这两个库展开。
sklearn中KNN相关类库:在scikit-learn 中,与近邻法这一大类相关的库都在sklearn.neighbors包之中。KNN分类树的类是KNeighborsClassifier,KNN回归树的类是KNeighborsRegressor。除此之外,还有KNN的扩展,即限定半径最近邻分类树的类RadiusNeighborsClassifier和限定半径最近邻回归树的类RadiusNeighborsRegressor, 以及最近质心分类算法NearestCentroid。
在这些算法中,KNN分类和回归的类参数完全一样。限定半径最近邻法分类和回归的类的主要参数也和KNN基本一样。
比较特别是的最近质心分类算法,由于它是直接选择最近质心来分类,所以仅有两个参数,距离度量和特征选择距离阈值,比较简单,因此后面就不再专门讲述最近质心分类算法的参数。
另外几个在sklearn.neighbors包中但不是做分类回归预测的类也值得关注,kneighbors_graph类返回用KNN时和每个样本最近的K个训练集样本的位置,radius_neighbors_graph返回用限定半径最近邻法时和每个样本在限定半径内的训练集样本的位置。NearestNeighbors是个大杂烩,它即可以返回用KNN时和每个样本最近的K个训练集样本的位置,也可以返回用限定半径最近邻法时和每个样本最近的训练集样本的位置,常常用在聚类模型中,
PyOD中KNN相关的类库概述:里面就一个knn,用于对异常值的检测,继承的是scikit-learn中的NearestNeighbors,所以我们把scikit-learn中的KNN系列理解了,那异常检测也就是轻而易举的拿下了。
一、图解KNN有监督算法
当KNN用于有监督时,可以做分类,也可以回归,我们这里用分类举例,也就是喂给该算法模型的数据需要带有类别标签,为了方便算法的理解,我们虚构了如下的数据集:
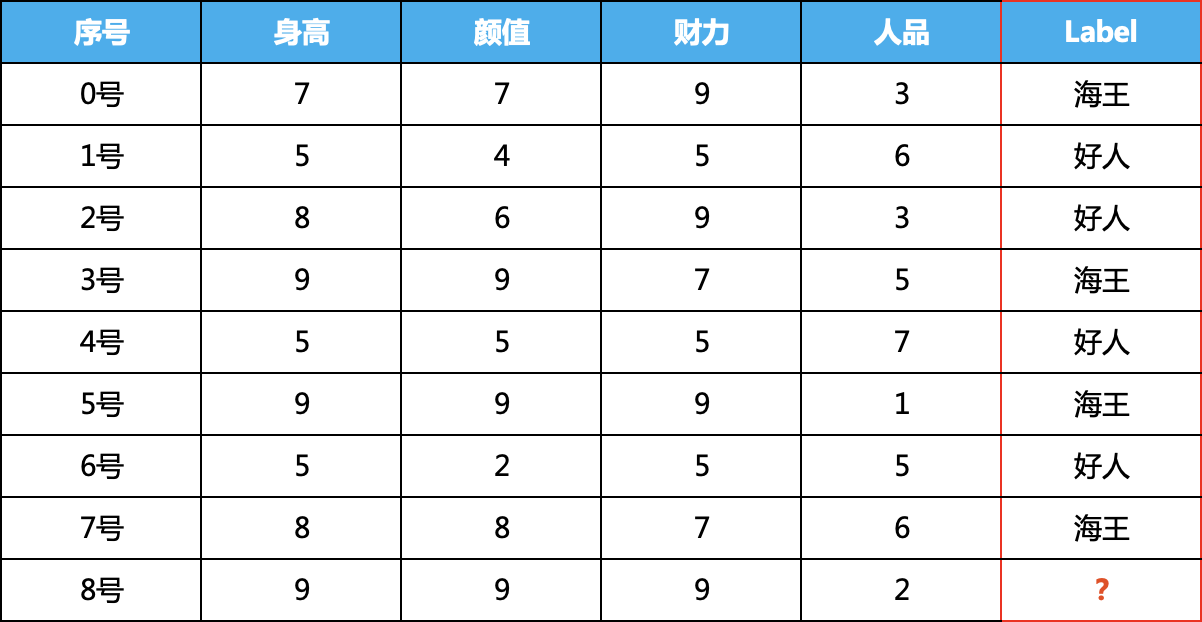
身高、颜值、财力、人品为数据集的特征,最后一列为label,我们需要根据0-7号男嘉宾的四个特征训练模型谁,判断8号男嘉宾是好人还是海王。
1、KNN原理
KKN原理:KNN算法非常简单粗暴,就是将预测点与所有训练集的点进行距离计算,然后保存并排序,选出前面K个值看看哪个类别比较多,就将预测点归于哪一类,如下图,原点为预测点,最近的三个样本,两个为红色三角形,那圆点的类别预测红色三角形类别。
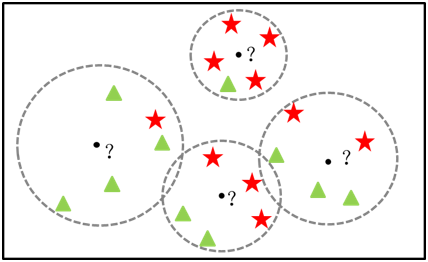
KNN过程:对未知类别的数据集中的每个点依次执行以下操作:
1) 计算当前点 与 已知类别数据集中每个点的距离
2) 按照距离递增次序排序
3) 选取与当前点距离最小的k个点
4) 确定前k个点所在类别的出现频率
5) 返回前k个点出现比例最高的类别作为当前点的预测类别
2、KNN实例讲解
这里会利用上诉的kNN数据集对KNN算法做逐步解释:
1) 计算预测点 与 已知类别数据集中的点之间的距离:
要度量空间中两个点的距离,有多种度量方式,常见的有曼哈顿距离、欧式距离等。KNN算法默认使用的是欧式距离,计算方法如下:

我们计算8号与每个样本之间的距离,计算结果如下:
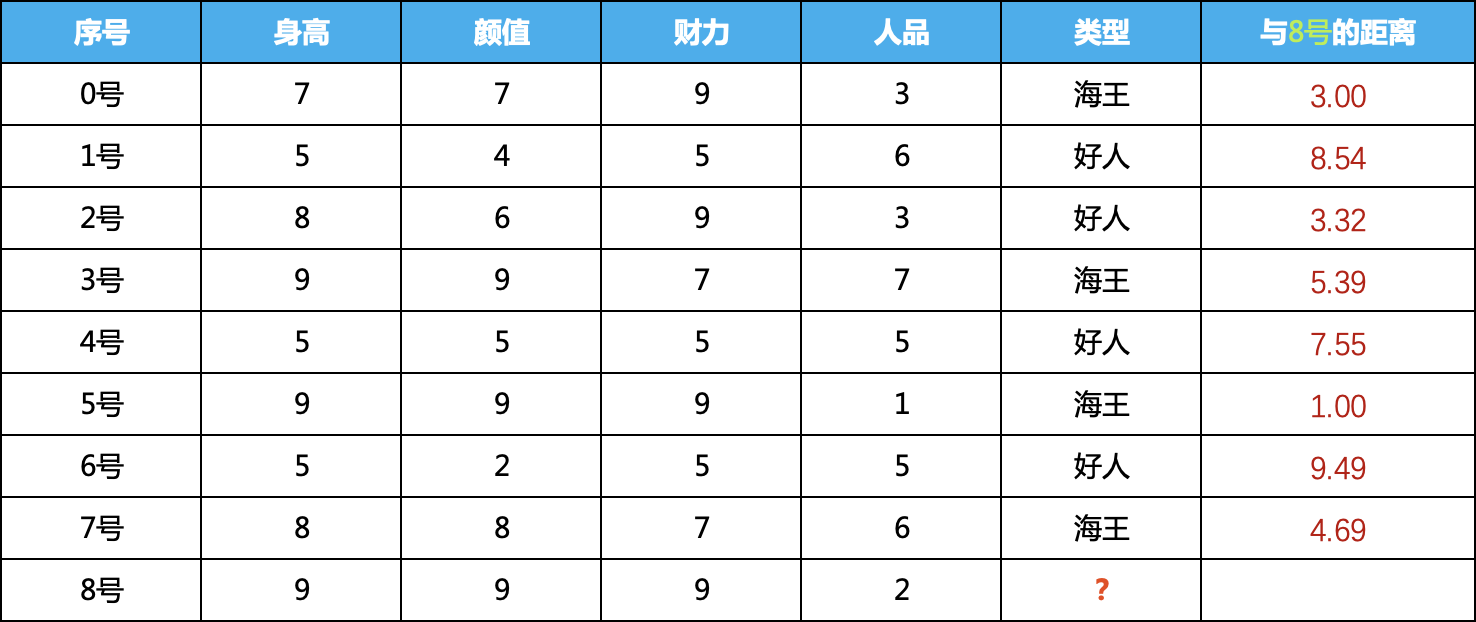
2) 按照计算的距离降序排列,看看谁与8号嘉宾的距离最近
按照与8号的距离排序,如下,可以看到,5号,0号,2号三个排的最近

3) 选取与预测点距离最小的k个点
我们知道K的取值比较重要,那么一般如何确定K的取值呢?答案是通过交叉验证,从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的准确率,最终找到一个比较合适的K值。我们这里取3和5分别看看预测的结果,大家对取不同的K值有个直观的感受。
K = 3

K = 5

4) 确定最近的k个邻居所在类别的频率
当 k = 3 的时候,包含2个海王和1个好人
好人的概率:1/3 = 0.3333
海王的概率:2/3 = 0.6666
当 k =5 的时候,包含4个海王和1个好人
好人的概率:1/5 = 0.2000
海王的概率:4/5 = 0.8000
由此可以看出来,k大小会影响我们对概率的判断,在本例中,不影响判断的类别,但是影响概率
5) 返回前k个点出现频率最高的类别作为当前点的预测分类
无论是k取3还是5,都是海王的概率大于好人的概率,因此我们对8号嘉宾的预测时海王,当然,最后的概率也可以输出是0.6666或者0.8.由此也可以看到,K值会比较大的影响预测结果
6)利用sklearn进行检验
我们手动算了上面的数据,现在用sklearn的算法检验我们的计算结果,看看有没有算对
# 构建数据集,按上面的表格
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 8, 7, 6]])
# 训练Label准备,1-海王,0-好人
y = [1, 0, 0, 1,0,1,0,1]
# 加载分类模型 k = 3
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
# 预测8号嘉宾 [[9, 9, 9, 2]] 的类别和概率
print(neigh.predict([[9, 9, 9, 2]]))
[1]
print(neigh.predict_proba([[9, 9, 9, 2]]))
[[0.33333333 0.66666667]]
# 加载分类模型 k = 5
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(X, y)
# 预测8号嘉宾 [[9, 9, 9, 2]] 的类别和概率
print(neigh.predict([[9, 9, 9, 2]]))
[1]
print(neigh.predict_proba([[9, 9, 9, 2]]))
[[0.2 0.8]]
简直完美,和我们手动计算的一模一样,到此,我们就算理解了基础的KNN算法,当然,应用的时候,涉及到更多的数据处理以及更多的参数,我们在下面贴出来。我们上面用分类任务举例,其实对于回归任务,我们只要找到最近的邻居,然后按邻居的取值取平均值或者中位数就可以了。
二、KNN有监督算法应用
KNN用于有监督算法主要有五个,分类的类是KNeighborsClassifier,回归的类是KNeighborsRegressor,除此之外,还有KNN的扩展,即限定半径最近邻分类的类RadiusNeighborsClassifier和限定半径最近邻回归树的类RadiusNeighborsRegressor, 以及最近质心分类算法NearestCentroid。我们下面看看这个五个算法的基本用法和案例。
1、KNeighborsClassifier
1)基本用法
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)参数详解
n_neighbors: 默认为5, 就是k-NN的k的值, 选取最近的k个点
weights: 默认是uniform, 参数可以是uniform、distance, 也可以是用户自己定义的函数
- uniform: 是均等的权重, 就说所有的邻近点的权重都是相等的
- distance: 是不均等的权重, 距离近的点比距离远的点的影响大
- 用户自定义的函数, 接收距离的数组, 返回一组维数相同的权重
algorithm: 快速k近邻搜索算法, 默认参数为auto, 可以理解为算法自己决定合适的搜索算法. 除此之外, 用户也可以自己指定搜索算法: ball_tree、kd_tree、brute方法进行搜索.
- kd_tree: 构造kd树存储数据以便对其进行快速检索的树形数据结构. kd树也就是数据结构中的二叉树. 以中值切分构造的树, 每个结点是一个超矩形, 在维数小于20时效率高
- ball_tree: 是为了克服kd树高纬失效而发明的,其构造过程是以质心 C 和半径 r 分割样本空间, 每个节点是一个超球体
- brute: 是蛮力搜索, 也就是线性扫描, 当训练集很大时, 计算非常耗时
leaf_size: 默认是30, 这个是构造的kd树和ball树的大小. 这个值的设置会影响树构建的速度和搜索速度, 同样也影响着存储树所需的内存大小. 需要根据问题的性质选择最优的大小
p : minkowski距离度量里的参数. p=2时是欧氏距离, p=1时是曼哈顿距离,对于任意p, 就是minkowski距离
metric: 用于距离度量, 默认的度量是minkowski距离 (也就是L_p距离), 当p=2时就是欧氏距离
metric_params: 距离公式的其他关键参数. 默认为None
n_jobs: 并行处理的个数. 默认为1. 如果为-1, 那么那么CPU的所有cores都用于并行工作
3)Attributes-属性
effective_metric_:模型计算距离是用的距离类型
effective_metric_params_:模型计算距离是用的距离类型
n_features_in_:训练集用的特征数量
feature_names_in_:特征名称
n_samples_fit_:训练集中的样本数
4)Methods-方法
| fit(X, y) | 使用X作为训练数据,y作为目标值(类似于标签)来拟合模型。 |
| get_params([deep]) | 获取估值器的参数。 |
| kneighbors([X, n_neighbors, return_distance]) | 查找一个或几个点的K个邻居。 |
| kneighbors_graph([X, n_neighbors, mode]) | 计算在X数组中每个点的k邻居的(权重)图。 |
| predict(X) | 给提供的数据预测对应的标签。 |
| 返回测试数据X的概率估值。 | |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均准确值。 |
| set_params(**params) | 设置估值器的参数 |
2、KNeighborsRegressor
1)基本用法
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)参数详解
通上,KNeighborsClassifier,回归的参数和分类的参数一模一样,无须赘述,看上面的数据就行。
3)案例分析
X = [[0], [1], [2], [3]] y = [0, 0, 1, 1] from sklearn.neighbors import KNeighborsRegressor neigh = KNeighborsRegressor(n_neighbors=2) neigh.fit(X, y) KNeighborsRegressor(n_neighbors=2) print(neigh.predict([[1.5]])) [0.5]
3、RadiusNeighborsClassifier
除了上面KNeighborsClassifier 和 KNeighborsRegressor,与之对应的还有RadiusNeighborsClassifier 和 RadiusNeighborsRegressor,那么他们之间有什么区别呢?一个是靠半径来确定最近邻居,确定半径,有多少算多少,通过半径内的邻居确定预测数据的类别或者回归值,一个是靠K值来确定邻居,K几个就取几个,不管跨度有多大,就是要找到K个才罢休,然后根据找到的K个计算预测数据的类别或者回归值,具体用法和参数我们看下面的介绍。
1)基本用法
sklearn.neighbors.RadiusNeighborsClassifier(radius=1.0, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', outlier_label=None, metric_params=None, n_jobs=None, **kwargs)
2)参数注释
radius:寻找最邻近数据点的半径,半径的选择与样本分布有关,可以通过交叉验证来选择一个较小的半径,尽量保证每类训练样本其他类别样本的距离较远,默认值是1.0。如果数据是三维或者三维以下的,可以通过可视化观察来调参。
weights: 默认是uniform, 参数可以是uniform、distance, 也可以是用户自己定义的函数
- uniform: 是均等的权重, 就说所有的邻近点的权重都是相等的
- distance: 是不均等的权重, 距离近的点比距离远的点的影响大
- 自定义:用户自定义的函数, 接收距离的数组, 返回一组维数相同的权重
选择默认的"uniform",意味着所有最近邻样本权重都一样,在做预测时一视同仁。如果是"distance",则权重和距离成反比例,即距离预测目标更近的近邻具有更高的权重,这样在预测类别或者做回归时,更近的近邻所占的影响因子会更加大。当然,我们也可以自定义权重,即自定义一个函数,输入是距离值,输出是权重值。这样我们可以自己控制不同的距离所对应的权重。一般来说,如果样本的分布是比较成簇的,即各类样本都在相对分开的簇中时,我们用默认的"uniform"就可以了,如果样本的分布比较乱,规律不好寻找,选择"distance"是一个比较好的选择。如果用"distance"发现预测的效果的还是不好,可以考虑自定义距离权重来调优这个参数。
algorithm: 快速k近邻搜索算法, 默认参数为auto, 可以理解为算法自己决定合适的搜索算法. 除此之外, 用户也可以自己指定搜索算法: ball_tree、kd_tree、brute方法进行搜索。
- kd_tree: 构造kd树存储数据以便对其进行快速检索的树形数据结构, kd树也就是数据结构中的二叉树. 以中值切分构造的树, 每个结点是一个超矩形, 在维数小于20时效率高
- ball_tree: 是为了克服kd树高纬失效而发明的,其构造过程是以质心 C 和半径 r 分割样本空间, 每个节点是一个超球体
- brute: 是蛮力搜索, 也就是线性扫描, 当训练集很大时, 计算非常耗时
leaf_size: 默认是30, 这个是构造的kd树和ball树的大小. 这个值的设置会影响树构建的速度和搜索速度, 同样也影响着存储树所需的内存大小. 需要根据问题的性质选择最优的大小
outlier_label:主要用于预测时,如果目标点半径内没有任何训练集的样本点时,应该标记的类别,不建议选择默认值 none,因为这样遇到异常点会报错。一般设置为训练集里最多样本的类别。
p : minkowski距离度量里的参数. p=2时是欧氏距离, p=1时是曼哈顿距离,对于任意p, 就是minkowski距离
metric: 用于距离度量, 默认的度量是minkowski距离 (也就是L_p距离), 当p=2时就是欧氏距离
metric_params: 距离公式的其他关键参数,默认为None
n_jobs: 并行处理的个数. 默认为1, 如果为-1, 那么那么CPU的所有cores都用于并行工作
3)属性详解
classes_:类别数量
effective_metric_:使用的距离度量。 它将与度量参数相同或与其相同,例如 如果metric参数设置为“ minkowski”,而p参数设置为2,则为“ euclidean”。
effective_metric_params_:度量功能的其他关键字参数。 对于大多数指标而言,它与metric_params参数相同,但是,如果将valid_metric_属性设置为“ minkowski”,则也可能包含p参数值。
n_features_in_:多少个特征
feature_names_in_:特征的名称
n_samples_fit_:训练集的样本数
outlier_label_:不在半径内的数据怎么处理
outputs_2d_:如果在拟合期间y的形状为(n_samples,)或(n_samples,1),则为True。
4)方法详解
| fit(X, y) | Fit the radius neighbors classifier from the training dataset. |
| get_params([deep]) | Get parameters for this estimator. |
| predict(X) | Predict the class labels for the provided data. |
| Return probability estimates for the test data X. | |
| radius_neighbors([X, radius, ...]) | Find the neighbors within a given radius of a point or points. |
| radius_neighbors_graph([X, radius, mode, ...]) | Compute the (weighted) graph of Neighbors for points in X. |
| score(X, y[, sample_weight]) | Return the mean accuracy on the given test data and labels. |
| set_params(**params) | Set the parameters of this estimator. |
5)案例分析
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsClassifier
neigh = RadiusNeighborsClassifier(radius=1.0)
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
[0]
print(neigh.predict_proba([[1.0]]))
[[0.66666667 0.33333333]]
# 我把半径调小,就可以看到,找不到邻居会报错
neigh = RadiusNeighborsClassifier(radius=0.1)
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
No neighbors found for test samples array([0], dtype=int64), you can try using larger radius, giving a label for outliers, or considering removing them from your dataset.
# 我们可以设置下outlier_label这个参数,然后没有邻居的就默认一个类型了
neigh = RadiusNeighborsClassifier(radius=0.1,
outlier_label = 'most_frequent')
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
[0]
print(neigh.predict_proba([[1.0]]))
[[1. 0.]]
neigh.outlier_label_
[0]
# 其他方法
neigh = RadiusNeighborsClassifier(radius=1.0)
neigh.fit(X, y)
neigh.radius_neighbors([[1.3]])
(array([array([0.3, 0.7])], dtype=object),array([array([1, 2], dtype=int64)], dtype=object))
4、RadiusNeighborsRegressor
1)基本用法
sklearn.neighbors.RadiusNeighborsRegressor(radius=1.0, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)参数详解
参考RadiusNeighborsClassifier,参数少了outlier_label,因为无需分类,其他一模一样的参数、和方法
3)案例详解
X = [[0], [1], [2], [3]] y = [0, 0.5, 1.8, 2] from sklearn.neighbors import RadiusNeighborsRegressor neigh = RadiusNeighborsRegressor(radius=1.0) neigh.fit(X, y) print(neigh.predict([[1.3]])) [1.15]
5、NearestCentroid
常规的KNN分类,如果有1亿个训练样本,那么就要求计算1亿个距离,然后对这1亿个跨度进行排序,取最近的K个邻居,显然数量大了,算法运行效率就低了,基于此,质心分类提出了一种全新的思路,利用样本质心来判定类别,如果已知样本有1亿个,共有3个类别,先计算出3个质心,那么在进行分类时,只要把预测数据与3个类别的质心求3次距离并求一个最小值,这极大地提高了运行效率。示意图如下:
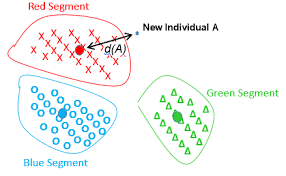
该 NearestCentroid 分类器是一个简单的算法, 它表示每个类都通过其成员的质心组成, 实际上, 这使得它类似于 KMeans算法的标签更新阶段,它也没有参数选择,使其成为良好的基准分类器。
1)基本用法
sklearn.neighbors.NearestCentroid(metric='euclidean', *, shrink_threshold=None)
星号(*):这是PEP-3102和Python3.0引入的一种新的函数参数规范语法,它指示KNeighborsClassifier类的构造函数在n_neighbors之后不接受任何其他位置参数,其余所有参数都是仅关键字的。仅关键字参数与名称和值一起提供,而位置参数则不必提供。在这种情况下,您可以合法地使用以下语法(为n_neighbors提供值)
2)参数说明
shrink_threshold:最近缩小质心, 它实现了 nearest shrunken centroid 分类器.,实际上, 每个质心的每个特征的值除以该特征的类中的方差, 然后通过shrink_threshold 来减小特征值, 最值得注意的是,如果特定特征值与零相交, 则将其设置为零. 实际上, 这将从影响的分类上删除该特征. 这是有用的, 例如, 去除噪声特征。
3)Attributes
centroids_:每个类别的质心
classes_:训练集类别的数量
n_features_in_:特征的数量
feature_names_in_:查看特征的名称
4)案例分析
from sklearn.neighbors import NearestCentroid
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])
clf = NearestCentroid()
clf.fit(X, y)
NearestCentroid()
print(clf.predict([[-0.8, -1]]))
[1]
# 查看质心
clf.centroids_
array([[-2. , -1.33333333],
[ 2. , 1.33333333]])
6、K值的确定
我们用数据集load_digits进行数据评估,使用常规的算法KNeighborsClassifier
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
# 查看下数据集的大小
X_digits.shape
(1797, 64)
# 数据集进行拆分,按3-7比例分为测试集+训练集
X_train, X_test, y_train, y_test = train_test_split(\
X_digits,
y_digits,
test_size=0.3,
random_state=250
)
# 寻找最优k值
best_s = 0
best_k = -1
k_list = [] #存储K值
s_list = [] #存储准确率值
for k in range(1,10):
clf = KNeighborsClassifier(k,weights='distance')
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
k_list.append(k)
s_list.append(score)
if score > best_s:
best_s = score
best_k = k
plt.plot(k_list, score_list, color='steelblue')
plt.show()
print('最好的参数k为{}'.format(best_k))
print('最好准确率为{}'.format(best_s))
最好的参数k为1
最好准确率为0.9907407407407407
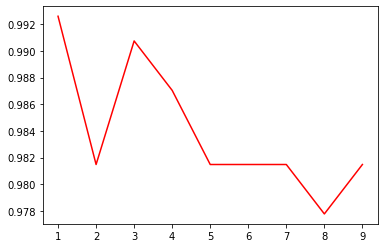
可以看出,k=1的时候,准确率最高,并且随着K的增加,准确率在不断的下降,这个数据比较特殊,一般都是K值取一个10左右比较高。对于自己的数据集,可以根据实际情况进行调整。
7、KNN优缺点
KNN算法真是个爱憎分明的算法,优点缺点都特别明显,哈哈,我找了一堆,大家可以慢慢体会,发现还是缺点多很多。具体总结如下,很多缺点也慢慢的进行了优化和解决。
1)优点
原理简单,易于理解和实现
无需参数,也不用实际进行训练
比较适用于多分类问题
kNN可以用来做无监督异常检验;
自适应kNN可以根据不同的区域,在局部选择不同的k
kNN非常适合做时间序列
2)缺点
基于KNN模型寻找异常点是不适合于高维数据和大批量数据的,kNN算法必须保存全部的数据集,如果训练数据集很大,那么就需要耗费大量的存储空间。此外,由于必须对待分类数据计算与每一个训练数据的距离,非常耗时。
而且距离的计算采用的是欧式距离公式,只能针对球形簇的样本数据寻找异常,对于非球形簇则无法很好的搜寻异常。
可解释性较差,无法给出决策树那样的规则,对变量的缩放非常敏感、无法处理categorical变量、难以处理不同单位和不同数值范围的变量
kNN还有个问题就是k的选择。k总是在过拟合与欠拟合之间游走。你可以说通过cross validation来选k,可是呢,你选出的k是全局适用的,而每个局部都是这个k最佳。所以kNN总是无法避免地在一些区域过拟合,同时在另一些区域欠拟合。
如果用K近邻模型做回归的话,一个比较明显的缺陷,就是K-NN无法做out of sample的回归预测。因为用K-NN做回归的时候,预测值是它附近几个值的平均值。所以预测值不可能超过预测样本的最大值,也不可能小于样本的最小值。这个缺点其实是和回归树一样的。
k太小,容易受到噪声数据影响,k太大可能在近邻中包含其它类别的点,可通过对距离加权解决,已经有这个参数了。
三、图解KNN异常检算法
KNN怎么进行无监督检测呢,其实也是很简单的,异常点是指远离大部分正常点的样本点,再直白点说,异常点一定是跟大部分的样本点都隔得很远。基于这个思想,我们只需要依次计算每个样本点与它最近的K个样本的平均距离,再利用计算的距离与阈值进行比较,如果大于阈值,则认为是异常点,同样,为了帮助读者理解如何利用KNN思想,实现异常值的识别,我画了下面这张图。对于第一个,3个邻居的平均距离为(2+2+3)/3=2.33,对于第二点,3个邻居的平均距离为(7+8+5)/3=6.667,明显,第二个点的异常程度要高与第一个点。
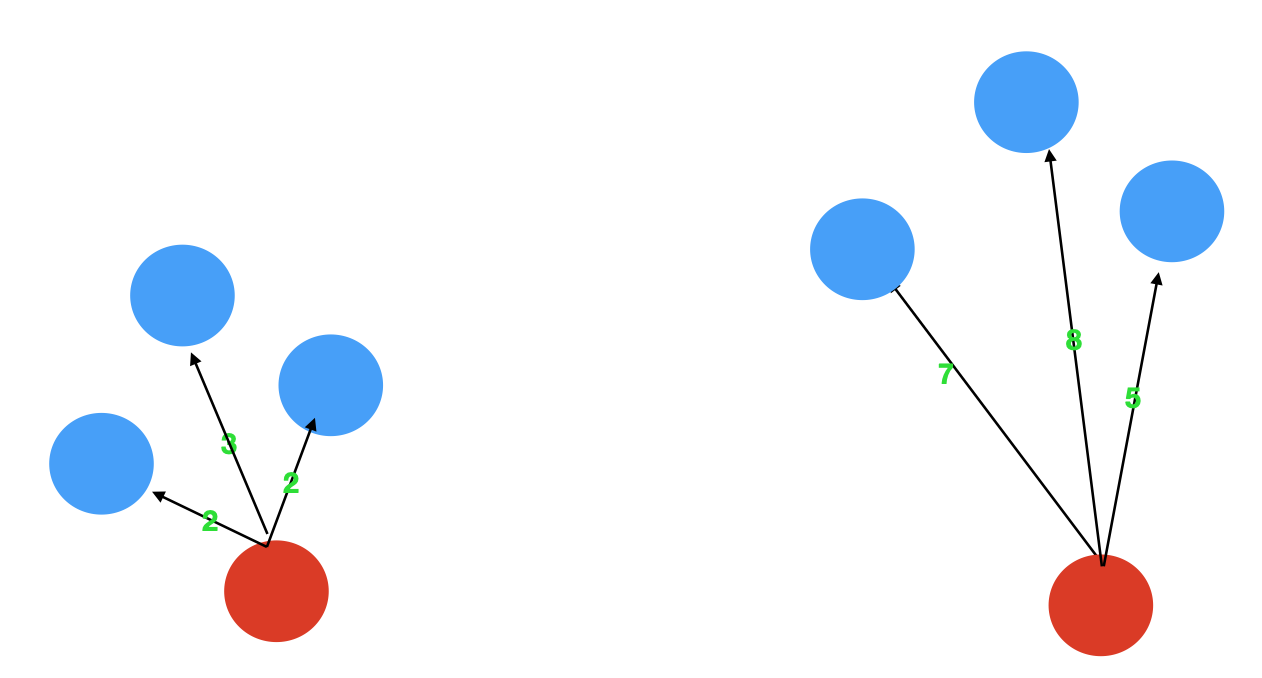
优点是不需要假设数据的分布,缺点是不适合高维数据、只能找出异常点,无法找出异常簇、你每一次计算近邻距离都需要遍历整个数据集,不适合大数据及在线应用、有人用hyper-grid技术提速将KNN应用到在线情况,但是还不是足够快,仅可以找出全局异常点,无法找到局部异常点。
KNN异常检测过程:对未知类别的数据集中的每个点依次执行以下操作:
1) 计算当前点 与 数据集中每个点的距离
2) 按照距离递增次序排序
3) 选取与当前点距离最小的k个点
4) 计算当前点与K个邻居的距离,并取均值、或者中值、最大值三个中的一个作为异常值
1、异常实例计算
无监督,我们就要标签去掉,为了演示过程,我们引进了9号嘉宾,这个人非常自信,每一项都填的非常高,明显异常,我们的目的就是要把这种类似的错误找出来。
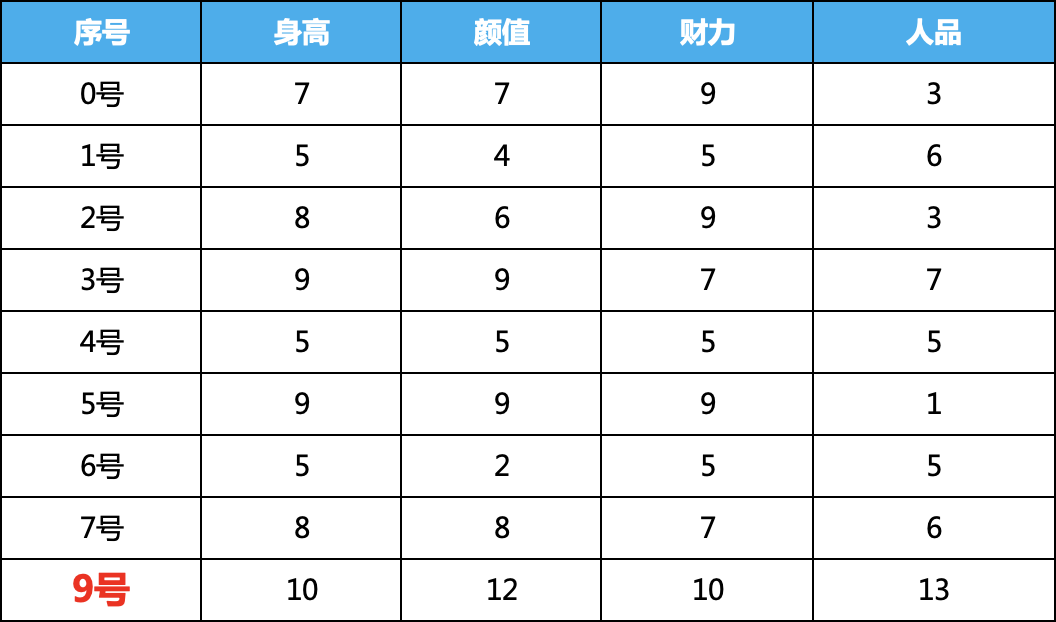
2、距离计算和排序
我们计算9号的异常程度,我们这里把计算和排序两步统一到一起了
先计算9号与其他样本的距离,然后排序,取最近的三个,我们计算平均距离,可以看到,9号与最近的三个邻居的平均距离是9.29
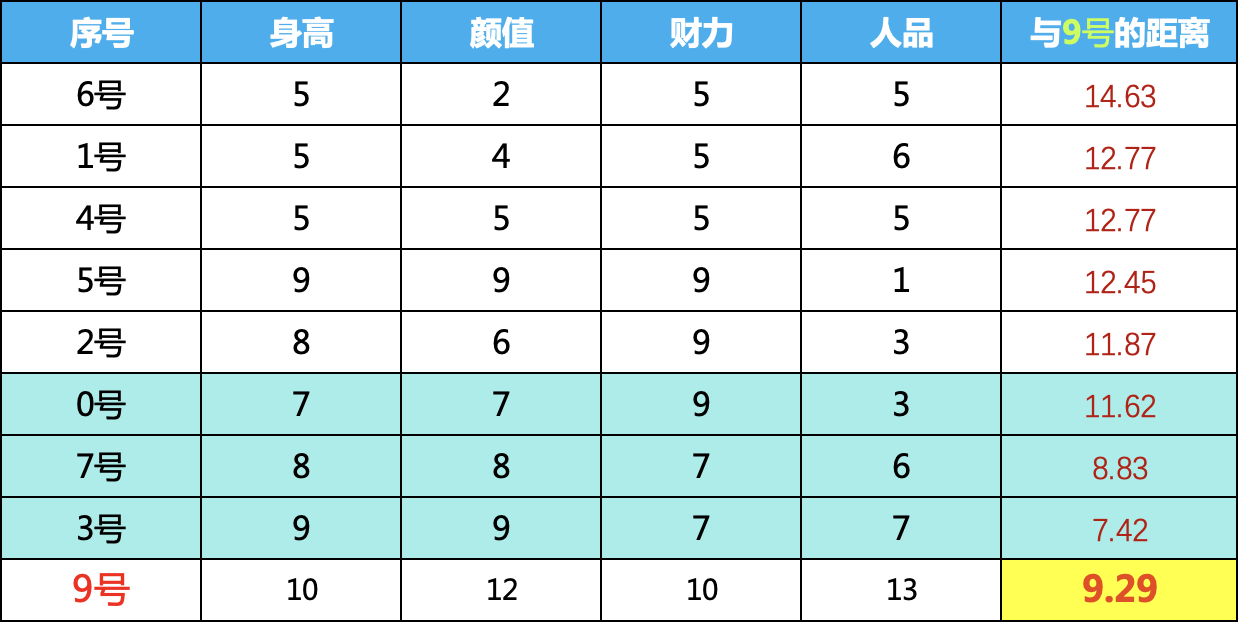
3、计算距离值
我们再计算4号嘉宾的距离,可以看到,最近的三个邻居与4号的平均距离为3.07,只是9号的三分之一,相对来说就比较正常了。当然距离计算可以用最大值,平均值,中位数三个,算法中通过method这个参数进行调节。
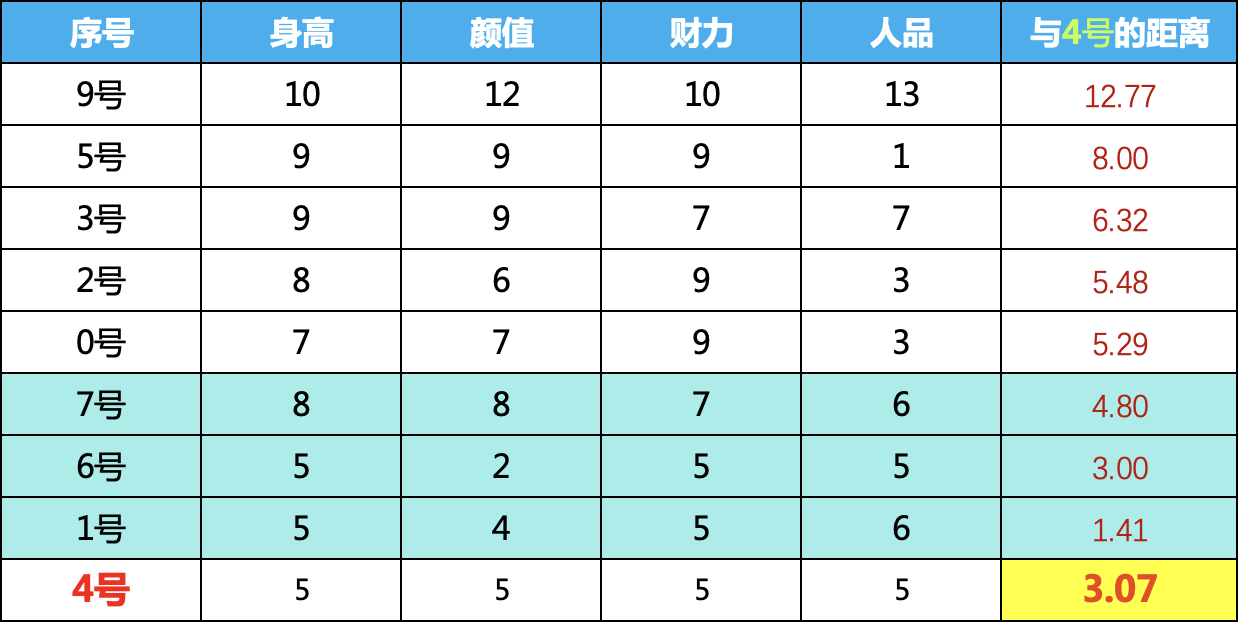
我们依次计算,就可以得到每个样本3个邻居的平均距离了,越高的越异常,我们也可以用Python的包来检测下我们计算的对不对。
import numpy as np
X_train = np.array([
[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 8, 7, 6],
[10,10, 12, 13]])
# import kNN分类器
from pyod.models.knn import KNN
# 训练一个kNN检测器
clf_name = 'kNN'
# 初始化检测器clf
clf = KNN( method='mean', n_neighbors=3, )
clf.fit(X_train)
# 返回训练数据X_train上的异常标签和异常分值
# 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_train_pred = clf.labels_
y_train_pred
array([0, 0, 0, 0, 0, 0, 0, 0, 1])
# 返回训练数据上的异常值 (分值越大越异常)
y_train_scores = clf.decision_scores_
y_train_scores
array([2.91709951, 3.01181545, 3.09299219, 4.16692633, 3.07001503,
4.25784112, 3.98142397, 3.24271326, 9.42068891])
我们自己计算的平均距离为9.29,系统算的9.42,有一点点的差异,可能是哪里加了一个微调的系数,大家可以探索下。
四、KNN异常检测算法应用
上面大概知道了KNN怎么进行异常检测的,现在我们找个具体的案例,看看更加明细的参数以及实现的过程,有个更加立体的感觉,并且学完能够应用起来。
1、算法基本用法
地址:All Models - pyod 1.0.0 documentation
pyod.models.knn.KNN(contamination=0.1,
n_neighbors=5,
method='largest',
radius = 1.0,
algorithm='auto',
leaf_size=30,
metric='minkowski',
p=2,
metric_params=None,
n_jobs=1,
**kwargs)
2、参数详解
contamination:污染度,contamination : float in (0., 0.5), optional (default=0.1)数据集的污染量,即数据集中异常值的比例。在拟合时用于定义决策函数的阈值。如果是“自动”,则确定决策函数阈值,如原始论文中所示。在版本0.20中更改:默认值contamination将从0.20更改为'auto'0.22。
n_neighbors:选取相邻点数量
method:‘largest’、‘mean’、‘median’
- largest:使用与第k个相邻点的距离作为异常得分
- mean:使用k个相邻点距离的平均值作为异常得分
- median:使用k个相邻点距离的中值作为异常得分
radius : radius_neighbors使用的参数空间半径
algorithm:找到最近的k个样本
- kd_tree:依次对K维坐标轴,以中值切分,每一个节点是超矩形,适用于低维(<20时效率最高)
- ball_tree:以质心c和半径r分割样本空间,每一个节点是超球体,适用于高维(kd_tree高维效率低)
- brute:暴力搜索
- auto:通过 fit() 函数拟合,选择最适合的算法;如果数据稀疏,拟合后会自动选择brute,参数失效
leaf_size:kd_tree和ball_tree中叶子大小,影响构建、查询、存储,根据实际数据而定。树叶中可以有多于一个的数据点,算法在达到叶子时在其中执行暴力搜索即可。如果leaf size 趋向于 N(训练数据的样本数量),算法其实就是 brute force了。如果leaf size 太小了,趋向于1,那查询的时候 遍历树的时间就会大大增加。
metric:距离计算标准,距离标准图例
- euclidean:欧氏距离(p = 2)
- manhattan:曼哈顿距离(p = 1)
- minkowski:闵可夫斯基距离
p : metric参数,默认为2
metric_params : metric参数
n_jobs : 并行作业数,-1时,n_jobs为CPU核心数。
3、属性详解
decision_scores_:数据X上的异常打分,分数越高,则该数据点的异常程度越高
threshold_:异常样本的个数阈值,基于contamination这个参数的设置,总量最多等于n_samples * contamination
labels_: 数据X上的异常标签,返回值为二分类标签(0为正常点,1为异常点)
4、方法详解
fit(X): 用数据X来“训练/拟合”检测器clf。即在初始化检测器clf后,用X来“训练”它。
fit_predict_score(X, y): 用数据X来训练检测器clf,并预测X的预测值,并在真实标签y上进行评估。此处的y只是用于评估,而非训练
decision_function(X): 在检测器clf被fit后,可以通过该函数来预测未知数据的异常程度,返回值为原始分数,并非0和1。返回分数越高,则该数据点的异常程度越高
predict(X): 在检测器clf被fit后,可以通过该函数来预测未知数据的异常标签,返回值为二分类标签(0为正常点,1为异常点)
predict_proba(X): 在检测器clf被fit后,预测未知数据的异常概率,返回该点是异常点概率
当检测器clf被初始化且fit(X)函数被执行后,clf就会生成两个重要的属性:
decision_scores: 数据X上的异常打分,分数越高,则该数据点的异常程度越高
KNN算法专注于全局异常检测,所以无法检测到局部异常。首先,对于数据集中的每条记录,必须找到k个最近的邻居。然后使用这K个邻居计算异常分数。
最 大:使用到第k个邻居的距离作为离群值得分
平均值:使用所有k个邻居的平均值作为离群值得分
中位数:使用到k个邻居的距离的中值作为离群值得分
在实际方法中后两种的应用度较高。然而,分数的绝对值在很大程度上取决于数据集本身、维度数和规范化。参数k的选择当然对结果很重要。如果选择过低,记录的密度估计可能不可靠。(即过拟合)另一方面,如果它太大,密度估计可能太粗略。K值的选择通常在10-50这个范围内。所以在分类方法中,选择一个合适的K值,可以用交叉验证法。
但是,事实上基于KNN的算法都是不适用于欺诈检测的,因为他们本身就对噪声比较敏感。
5、案例分析
#导入
from pyod.models.knn import KNN
from pyod.utils.data import generate_data
from pyod.utils.data import evaluate_print
from pyod.utils.example import visualize
#参数设置
contamination = 0.1 # percentage of outliers
n_train = 200 # number of training points
n_test = 100 # number of testing points
X_train, y_train, X_test, y_test = generate_data(
n_train=n_train, n_test=n_test, contamination=contamination)
# import kNN分类器
from pyod.models.knn import KNN
# 训练一个kNN检测器
clf_name = 'kNN'
clf = KNN() # 初始化检测器clf
clf.fit(X_train) # 使用X_train训练检测器clf
# 返回训练数据X_train上的异常标签和异常分值
y_train_pred = clf.labels_ # 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_train_scores = clf.decision_scores_ # 返回训练数据上的异常值 (分值越大越异常)
# 用训练好的clf来预测未知数据中的异常值
y_test_pred = clf.predict(X_test) # 返回未知数据上的分类标签 (0: 正常值, 1: 异常值)
y_test_scores = clf.decision_function(X_test) # 返回未知数据上的异常值 (分值越大越异常)
对识别结果可视化
# 模型可视化
visualize(clf_name,
X_train,
y_train,
X_test,
y_test,
y_train_pred,
y_test_pred,
show_figure=True,
save_figure=False
)
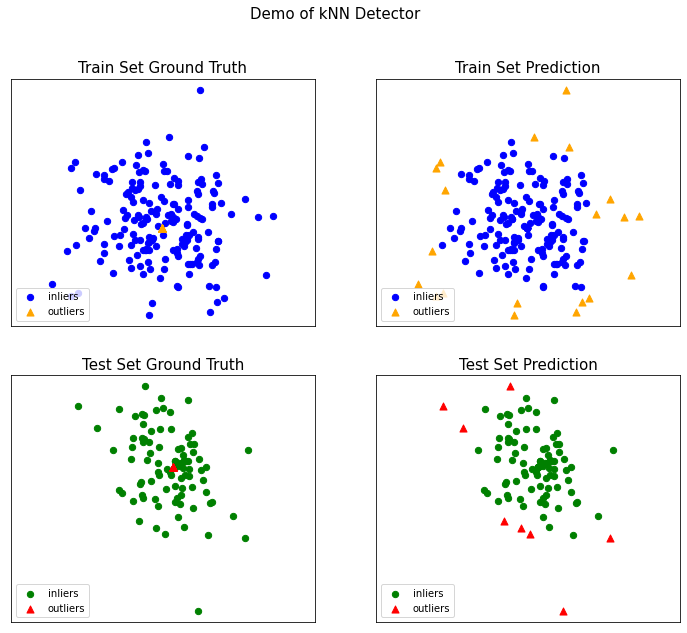
五、KNN的其他用途
KNN除了能够进行有监督,另外几个在sklearn.neighbors包中但不是做分类、回归预测的类也值得关注,用于寻找最邻近的数据点,是其他最邻近算法的基础。kneighbors_graph类返回用KNN时和每个样本最近的K个训练集样本的位置。radius_neighbors_graph返回用限定半径最近邻法时和每个样本在限定半径内的训练集样本的位置。NearestNeighbors是个大杂烩,它即可以返回用KNN时和每个样本最近的K个训练集样本的位置,也可以返回用限定半径最近邻法时和每个样本最近的训练集样本的位置,常常用在聚类模型中。
许多学习方法都是依赖最近邻作为核心。 一个例子是 核密度估计 和LOF, 这两个我们在其他地方再讨论
1、NearestNeighbors
NearestNeighbors (最近邻)寻找N个最近的邻居以及计算之间的距离,实现了 unsupervised nearest neighbors learning(无监督的最近邻学习)。 它为三种不同的最近邻算法提供统一的接口:BallTree, KDTree, 还有基于 sklearn.metrics.pairwise 的 brute-force 算法。选择算法时可通过关键字 'algorithm' 来控制, 并指定为 ['auto', 'ball_tree', 'kd_tree', 'brute'] 其中的一个即可。当默认值设置为 'auto' 时,算法会尝试从训练数据中确定最佳方法。
1)基本用法
sklearn.neighbors.NearestNeighbors(*, n_neighbors=5, radius=1.0, algorithm='auto', leaf_size=30, metric='minkowski', p=2, metric_params=None, n_jobs=None)
2)参数含义
n_neighbors(n邻域):所要选用的最近邻的数目,相当于knn算法(k近邻算法)中的 k,(default = 5),在设置此参数时输入的需为整形(int)。
radius(半径):要使用的参数空间范围,在设置此参数时输入的需为浮点数(float)。
algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}:即用于选取计算最近邻的算法:这里主要包括
‘auto’ :根据样本数据自动刷选合适的算法。
‘ball_tree’:构建“球树”算法模型。
‘kd_tree’ :‘’kd树‘’算法。
‘brute’ :使用蛮力搜索,即或相当于Knn算法,需遍历所有样本数据与目标数据的距离,进而按升序排序从而选取最近的K个值,采用投票得出结果。
leaf_size:叶的大小,针对算法为球树或KD树而言。这个设置会影响构造和查询的速度,以及存储树所需的内存。最优值取决于问题的性质。
metric:用于树的距离度量。默认度量是Minkowski,p=2等价于标准的欧几里德度量。有关可用度量的列表,可以查阅距离度量类的文档。如果度量是“预先计算的”,则假定X是距离矩阵,在拟合期间必须是平方。
p:Minkowski度量参数的参数来自sklearn.emeics.pairwise.pairwise_距离。当p=1时,这等价于使用曼哈顿距离(L1),欧几里得距离(L2)等价于p=2时,对于任意的p,则使用Minkowski_距离(L_P)。
metric_params:度量函数的附加关键字参数,设置应为dict(字典)形式。
n_jobs:要为邻居搜索的并行作业的数量。None指1,除非在 joblib.parallel_backend背景。-1意味着使用所有处理器,若要了解相关的知识应该具体查找一下。
3)案例解析
from sklearn.neighbors import NearestNeighbors
import numpy as np
#定义一个数组
X = np.array([[-1,-1],
[-2,-1],
[-3,-2],
[1,1],
[2,1],
[3,2] ])
nbrs = NearestNeighbors(n_neighbors=3, algorithm= 'ball_tree').fit(X)
distances, indices = nbrs.kneighbors(X)
# 训练一个模型,并计算距离
samples = [[0, 0, 2], [1, 0, 0], [0, 0, 1]]
neigh = NearestNeighbors(n_neighbors=2,
radius=0.4,
algorithm='ball_tree')
neigh.fit(samples)
neigh.kneighbors([[0, 0, 1.3]], 2,
return_distance=True, )
distances, neighs = neigh.kneighbors([[0, 0, 1.3]], 2, return_distance=True, )
distances
array([[0.3, 0.7]])
neighs
array([[2, 0]], dtype=int64)
from sklearn.neighbors import NearestNeighbors import numpy as np X = np.array([ [7, 7, 9, 3], [5, 4, 5, 6], [3, 6, 6, 9], [9, 9, 7, 5], [5, 5, 5, 5], [9, 9, 9, 1], [5, 2, 5, 5], [8, 8, 7, 6]]) nbrs = NearestNeighbors(n_neighbors=3, algorithm= 'ball_tree').fit(X) distances, indices = nbrs.kneighbors([[9, 9, 9, 2]])
2、KDTree 和 BallTree 类
我们可以使用 KDTree 或 BallTree 其中一个类来找最近邻。 这是上文使用过的 NearestNeighbors 类所包含的功能。KDTree 和 BallTree 具有相同的接口; 我们将在这里展示使用 KDTree 的例子
1)BallTree
sklearn.neighbors.BallTree(X, leaf_size=40, metric='minkowski', **kwargs)
21)KDTree
sklearn.neighbors.KDTree(X, leaf_size=40, metric='minkowski', **kwargs)¶
3)案例应用
from sklearn.neighbors import KDTree
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
kdt = KDTree(X, leaf_size=30, metric='euclidean')
kdt.query(X, k=2, return_distance=False)
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]]...)
计算距离,方便其他算法进行调用。
3、kneighbors_graph
k-近邻图(k-nearest neighbor graph),选定参数k,对于顶点vi,i=1,..,n,把离它最近的k个点与之相连,所得到的图就是k-近邻图。需要注意的是,因为这样的邻近关系并不是对称的(vj是vi的k近邻 ≠vi是vj的k近邻),故而得到的图将会是“有向”的。为了得到无向的图(图的赋权邻接矩阵W应是对称的)
1)基本用法
sklearn.neighbors.kneighbors_graph(X, n_neighbors, *, mode='connectivity', metric='minkowski', p=2, metric_params=None, include_self=False, n_jobs=None)
2)参数详解
X:样本数据,以numpy数组或预先计算的BallTree的形式。
n_neighbors:每个样本的邻居数量。
mode:'connectivity'将返回具有1和0的连通性矩阵,而'distance'将根据给定的度量返回邻居之间的距离。
metric:用于计算每个采样点的k邻居的距离度量。DistanceMetric类提供了可用指标的列表。默认距离为'euclidean'(“ minkowski”度量标准,p参数等于2。)
p:Minkowski度量的功率参数。当p=1时,相当于使用manhattan_distance (l1),p=2时使用欧氏距离(l2)。对于任意的p,使用minkowski_distance (l_p)。
metric_params:计量函数的附加关键字参数。
include_self:是否将每个样本标记为其自身的第一个最近邻居。如果为'auto',则将True用于mode ='connectivity',将False用于mode ='distance'。
n_job:为邻居搜索运行的并行作业数。 None 意味着 1 除非在joblib.parallel_backend上下文中。 -1 表示使用所有处理器。
返回值:图形,其中A[i,j]被赋予连接i和j的边的权重,矩阵为CSR格式。
3)案例数据
可以看到,这里的联通,包含了自己,当邻居等于1的时候,只有自己和自己联通
X = [[0], [3], [1]]
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X, 2, mode='connectivity', include_self=True)
A.toarray()
array([[1., 0., 1.],
[0., 1., 1.],
[1., 0., 1.]])
X = [[0], [3], [1]]
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X,1, mode='connectivity', include_self=True)
A.toarray()
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
4)数据可视化
networkx 画图布局_ACxz的博客-CSDN博客_networkx布局
import networkx as nx
import matplotlib.pyplot as plt
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 2, 7, 6],
[1, 8, 7, 4],
[4, 3, 7, 8],
[8, 1, 7, 6]
])
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X, 4, mode='connectivity', include_self=False)
# 绘图
G = nx.from_numpy_matrix(A.toarray())
plt.figure(figsize=(4,4),dpi=600)
nx.draw_networkx(G,
pos = nx.kamada_kawai_layout(G),
node_color = 'r',
node_size=500,
alpha=0.8
)
plt.axis('off')
plt.show()
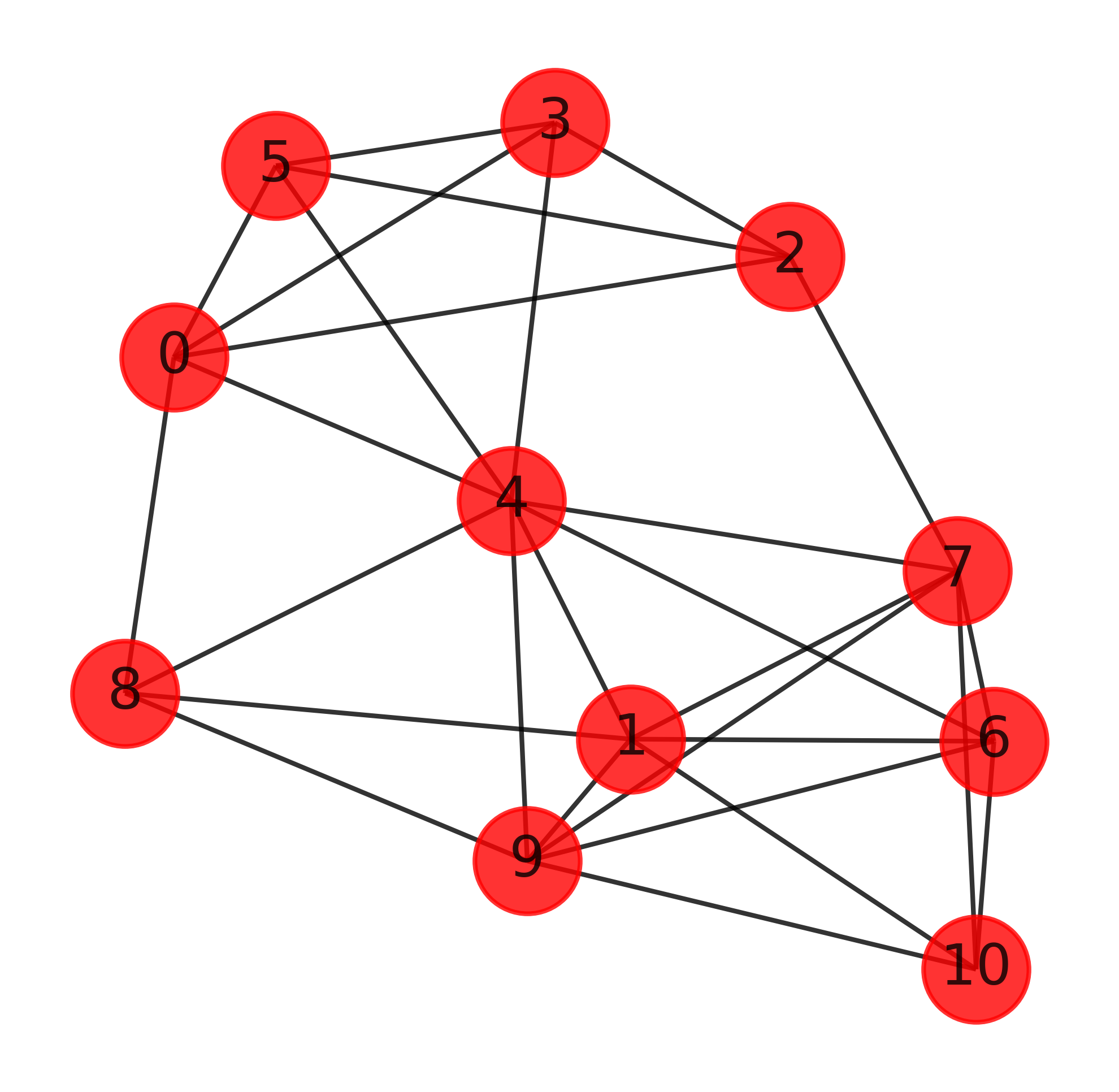
我们这里的图比较简单,如果继续增加复杂度,画出的图如下,大家可以找比较大的数据集进行测试,文章写的太多了,不能再写下去了。KNN写成图算法了。

Distributed k-nn graphs and similarity search | cylab.be
4、radius_neighbors_graph
1)基本用法
sklearn.neighbors.radius_neighbors_graph(X, radius, *, mode='connectivity', metric='minkowski', p=2, metric_params=None, include_self=False, n_jobs=None)
2)参数详解
参考kneighbors_graph,除了半径限制参数radius,其他的参数均一模一样,这里不再赘述。
3)应用案例
X = [[0], [3], [1]]
from sklearn.neighbors import radius_neighbors_graph
A = radius_neighbors_graph(X, 1.5, mode='connectivity',
include_self=True)
A.toarray()
array([[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
4)可视化
import networkx as nx
import matplotlib.pyplot as plt
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 2, 7, 6],
[1, 8, 7, 4],
[4, 3, 7, 8],
[8, 1, 7, 6]
])
from sklearn.neighbors import kneighbors_graph
A = radius_neighbors_graph(X, 4, mode='connectivity', include_self=False)
# 绘图
G = nx.from_numpy_matrix(A.toarray())
plt.figure(figsize=(4,4),dpi=600)
nx.draw_networkx(G,
pos = nx.kamada_kawai_layout(G),
node_color = 'r',
node_size=500,
alpha=0.8
)
plt.axis('off')
plt.show()

可以看到,我们的半径设置为4,有的节点并没有找到邻居,我们自己的用户或者文本数据,也是可以通过构建类似的矩阵,然后计算每个样本的K相似或者半径相识,这样就能够一目了然的找出一堆样本相互之间的关系了,并且还可以考虑其中的权重。
六、总 结
通过本文,我们发现KNN系列是一个非常丰富且有意思的内容,还有很多有待我们去探索。很多算法,其实学的是思想,如果认真的彻底搞清楚几个算法的原理,你会瞬间觉得,学其他算法也简单起来,如果你没有深刻的学过几个算法,总觉得学啥都是朦朦胧胧,似懂非懂的,好像什么都会了,好像又啥都不会。
思考题:KNN是不是也可以做个KNN森林,如果可以,怎么做,如果不行,为什么?看完本文来做这个思考题。
七、数据表附件
| 序号 | 身高 | 颜值 | 财力 | 人品 | 类型 |
| 1号 | 7 | 7 | 9 | 3 | 海王 |
| 2号 | 5 | 4 | 5 | 6 | 好人 |
| 3号 | 3 | 6 | 6 | 9 | 好人 |
| 4号 | 9 | 9 | 7 | 5 | 海王 |
| 5号 | 5 | 5 | 5 | 5 | 好人 |
| 6号 | 9 | 9 | 9 | 1 | 海王 |
| 7号 | 5 | 2 | 5 | 5 | 好人 |
| 8号 | 8 | 8 | 7 | 6 | 海王 |
| 9号 | 9 | 9 | 9 | 2 | ? |


