dB（分贝）定义及其应用_db和dba的区别

目录

1.1 dB的诞生背景

1.2 dB的定义

1.3 dB的应用

1.4 dBA

1.5dB叠加

参考文章：

---

1.1 dB的诞生背景

dB是英文“decibel”的简写，其中deci表示十分之一，Bel表示“贝”。Decibel，分贝就是十分之一贝。 “贝”是“贝尔”的简称，是以杰出科学家Alexander Graham Bell的名字来命名的单位。贝尔在1876年获得了电话发明的专利，并在电话的应用和发展上做出了巨大的突破。Bel并不是国际单位制（System International）的单位，但是受到国际单位制的规则影响，用人名表示的单位符号的首字母要大写，所以我们看到dB中B应为大写。由于“Bel”这个单位比较大，使用不方便，更常用的是十分之一贝尔，即分贝。

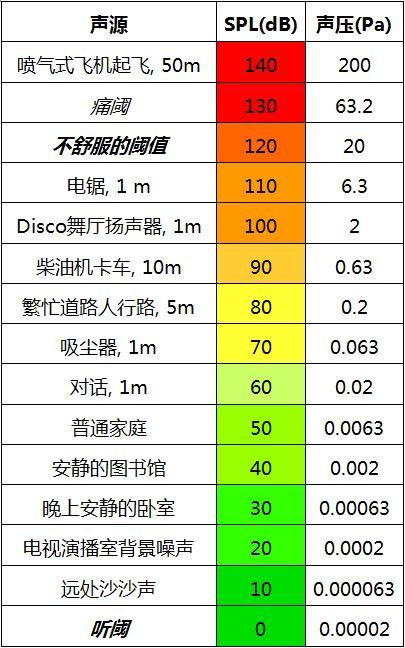
今天在音频工程和声学领域中，工程师、音响师几乎每天都会用到dB这个词。比如“将1000Hz衰减3dB”，“把推子推高3dB”，或者“这款音箱灵敏度是98dB SPL”，可以说dB在音频行业中是个无处不在的单位。而关于dB的讨论也是一个历久常新的话题，因为每一位从业者都会经历一个“搞懂dB是什么”的阶段，尤其是在声学领域，dB经常用作为表征声压级SPL（Sound Pressure Level）的大小。声压的单位是帕斯卡，Pa，声压的参考值是20μPa，这个值表示人耳在1000Hz处的平均可听阈值，或者是人耳在1000Hz处可被感知的平均最小声压波动值。声音是叠加在大气压之上的声压波动，大气压为1.01325×10^5Pa。相比于大气压，声压幅值波动非常小。人耳可听的声压幅值波动范围为2×10^-5Pa~20Pa，这个声压幅值波动区间很大，二者的比值达到了10^6。似乎从线性角度来说这个声压幅值的波动区间，很不方便。数字位数一多，读起来都头痛，要仔细逐一数一数位数，我反正是这样的，我不知道您是不是也是这样！有没有懒人方法呢，能方便的反映出这个波动的幅值呢？大师Bell早就在思考：有没有好的方法解决这个问题。因此，引入了以dB表示的声压级的概念。他发现我们人类耳朵对声音强度的反应是成对数形式的，大概意思就是当声音的强度增加到某一程度时，人的听觉会变的较不敏锐，刚好近似对数的单位刻度。这使得对数的单位可以拿来代表人类听觉变化的比例，因此，以对数dB形式表示的声压级应孕而生了。人耳可听的声压幅值波动范围为2×10^-5Pa~20Pa，用幅值dB表示对应的分贝数为0~120dB，因此，当用分贝表示声压级的大小时，表征起来更为方便。现实世界中各种常见情况中声音分贝大小如下图所示。

用图表表示声压幅值和分贝数如下表所示：

 

1.2 dB的定义

理解dB的第一个要点，就是要知道它是表示两个具有相同单位的同一种物理量的相对关系。即两种电或声功率之比或两种电压或电流值或类似声量之比。它还是一种测量声音相对响度的单位。最初在电话工程领域，dB是用于定义于表示两个功率比，是P1/P0的比值再取以10为底的对数，再乘以10，其数学式为：

dB是一个比值，是一个数值，是一个纯计数方法，没有任何单位标注。由于它在不同领域有着不同的名称，因此它也代表不同的实际意义。常见的领域有：声音、信号、增益等。

1.3 dB的应用

1、声音的大小

在实际日常生活中，住宅小区告知牌上面标示噪音要低于60分贝，也就是要低于60dB，在这里dB（分贝）的定义为噪声源功率与基准声功率比值的对数乘10的数值，不是一个单位，而是一个数值，用来形容声音的大小。

 

2、信号强度

在无线通讯领域，衡量一个地点的某一无线基站通信信号强度也可以用dB表示。如测的某宾馆402房间的1号无线基站通信信号强度为-90dBm,这里的定义为该房间的有用信号强度与所有信号（包括干扰信号）的比值。

3、增益

在天线技术方面，dB是衡量天线性能的一个参数，名称为增益。它是指在输入功率相等的条件下，实际天线与理想天线在空间同一点处所产生的信号的功率密度之比。

dB 是一个纯计数单位，在工程中有不同的定义方式（仅仅是看上去不同）。对于功率，dB = 10*log()。对于电压或电流，dB = 20*log()。

dB的意义其实再简单不过了，就是把一个很大（后面跟一长串0的）或者很小（前面有一长串0的）的数比较简短地表示出来。如（此处以功率为例）：

X = 100000 = 10*log(10^5) = 50 dB

X = 0.000000000000001 = 10*log(10^-15) = -150 dB

dBm 定义的是 miliwatt。 0 dBm = 10log(1) mW = 1 mW；

dBw 定义 watt。 0 dBw = 10log1 W = 10*log(1000) mw = 30 dBm。

dB在缺省情况下总是定义功率单位，以 10*log 为计。当然某些情况下可以用信号强度（Amplitude）来描述功和功率，这时候就用 20log 为计。不管是控制领域还是信号处理领域都是这样。比如有时候大家可以看到 dBmV 的表达。

在dB，dBm，dBw计算中，要注意基本概念。比如前面说的 0dBw = 10log1W = 10log1000mw = 30dBm；又比如，用一个dBm 减另外一个dBm时，得到的结果是dB。如：30dBm - 0dBm = 30dB。

一般来讲，在工程中，dB和dB之间只有加减，没有乘除。而用得最多的是减法：dBm 减 dBm 实际上是两个功率相除，信号功率和噪声功率相除就是信噪比（SNR）。dBm 加 dBm 实际上是两个功率相乘，这个已经不多见（我只知道在功率谱卷积计算中有这样的应用）。

简单地说，分贝就是放大器增益的单位。放大器输出与输入的比值为放大倍数，单位是“倍”，如10倍放大器，100倍放大器。当改用“分贝”做单位时，放大倍数就称之为增益，这是一个概念的两种称呼。电学中分贝与放大倍数的转换关系为：AV(I)(dB)=20lg[Vo/Vi(Io/Ii)]；Ap(dB)=10lg(Po/Pi)分贝定义时电压(电流)增益和功率增益的公式不同，但我们都知道功率与电压、电流的关系是P=V2/R=I2R。采用这套公式后，两者的增益数值就一样了：10lg[Po/Pi]=10lg(V2o/R)/(V2i/R)=20lg(Vo/Vi)。使用分贝做单位主要有三大好处。(1)数值变小，读写方便。电子系统的总放大倍数常常是几千、几万甚至几十万，一架收音机从天线收到的信号至送入喇叭放音输出，一共要放大2万倍左右。用分贝表示先取个对数，数值就小得多。附表为放大倍数与增益的对应关系。

运算方便。放大器级联时，总的放大倍数是各级相乘。用分贝做单位时，总增益就是相加。若某功放前级是100倍(20dB)，后级是20倍(13dB)，那么总功率放大倍数是100×20=2000倍，总增益为20dB＋13dB=33dB。

1.4 dBA

dBA是指对声音的A计权。通常对A计权的结果，用单位dBA或dB(A)来表示。
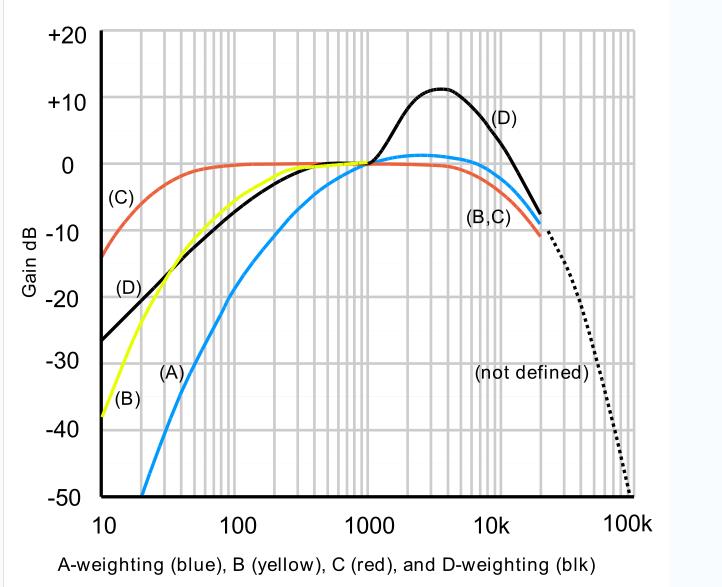
人耳可听的声音有一定的频率范围(20-20KHz)和一定的声压级范围(0-130dB)，如下图所示。

 

人耳不是对所有频率的敏感度都相同。正常人耳最敏感的频带是 3000 Hz 到 6000 Hz，它的频响会随着声音大小的变化而变化。通常，低频段和高频段声音感知能力不如中频段，效果是在低声压级更明显，在高声压级时会被压平，如图中各条曲线（等响曲线）所示，声压级越小的区间，曲线越陡峭，声压级越大的区段，曲线越平坦。

正是因为人耳对不同的频率，敏感度不一样，即使声压级的量级一样，听起来也不一样，所以，需要对真正听到的声压级通过增益因子进行修正，而用得最多的则是A计权。当然还有B，C，D计权。A计权对应的是40方的等响曲线，也就是上图中红色线条所表示的曲线。而B，C计权则对应70和100方的等响曲线，4种计权曲线如下图所示。

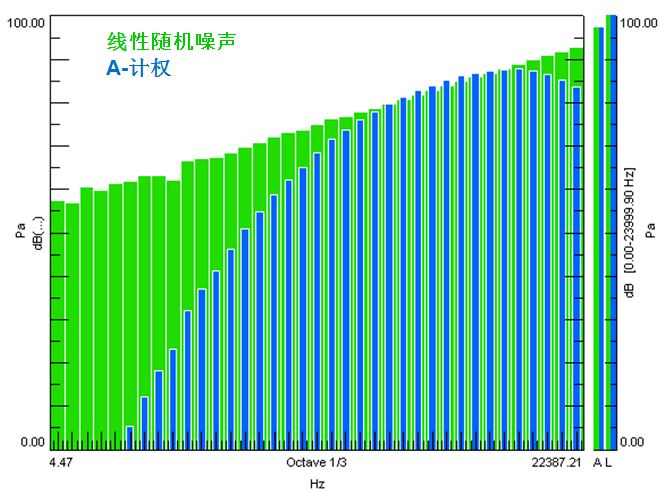
对同一信号采用不同的计权方式，最后得到的声压级是不一样的。如下图所示，对一随机信号计算不计权和A计权下的1/3倍频程曲线，可见二者差异明显。因此，当计权不同时，结果也是不同的。

除了dBA和其它三种计权之外，其实在其他领域还有dBm，dBW，dBu，dBv，dBi，dBd，dBc等等，但在NVH领域还是dBA最常用。

1.5dB叠加

dB可以任意相加吗？怎么相加？如70dB+60dB等于130dB吗？要是这么简单，世界就安静了，不会有那么多争论了，也不会有人说NVH是「玄学」了。

在这以声压级的叠加来进行说明。SPLresult=SPL1+SPL2+SPL3+…+SPLn？声压级的合成运算不是简单的加减运算，声压级不能直接相加，必须以能量形式相加计算，因此，声压级的合成公式如下

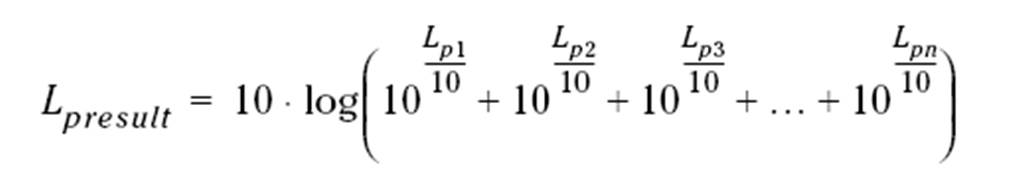
若两个声压级SPL1=SPL2=60dB，但两个声源是相关、同相位的，则合成后的声压级SPL为66dB，因为60dB对应0.02Pa，两个相加为0.04Pa，对应66dB。现实有这么美好吗？很少有相关同相位的两个声源，所以，这个等于白说了。是不是砍我的心都有了？ 若任意两个声压级SPL1=SPL2，则合成后的声压级为

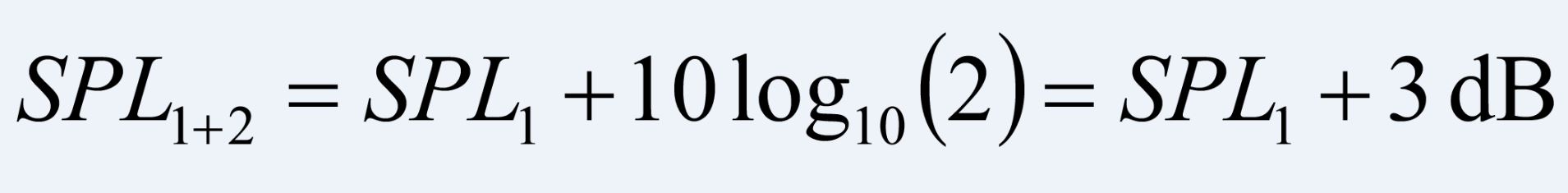
也就是说两个声压级相同，则合成后的声压级比之前大3dB。也可以用以下图来表示，横轴表示两个声压级的差值，纵轴表示在原来的基础上要增加多少dB。二者相差0dB时，合成之后大3dB, 当两个声压级相差15dB以上，数值小的声压级影响可以忽略。通过查询下图也可以求得合成后的声压级大小。

回到这一小节开始时提到的问题：70dB+60dB等于多少？我们可以根据这一节第一个公式计算或者对比上图可以得到结果为70.4dB，记住不是130dB。

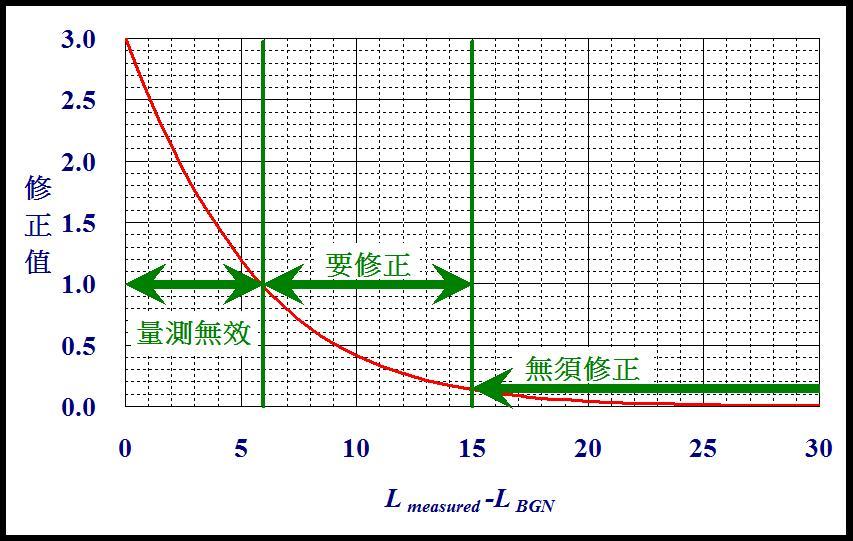
说完了声压级的合成，再说说声压级的分解吧。声压级的分解通常用于修正背景噪声的影响，如噪声测量值Lmeasured 修正背景噪音LBGN 的影响，不是简简单单地Lsource =Lmeasured-LBGN， 而是

 

国际规范中关于背景噪声的修正原则如下图表示。当背景噪音与声源的声压级差值小于6dB时，测量无效；当二者差值位于6~15dB之间时需要修正，修正按以上公式修正；当二者差值大于15dB时，可忽略背景噪声对测量结果的影响。

参考文章：

https://zhuanlan.zhihu.com/p/22821588

http://www.prozs.com/edu/detail.asp?id=1440

https://www.cnblogs.com/jsdy/p/12728493.html