- 1什么是全国大学生电子设计大赛?如何备战?_电赛测评一定要全队都去吗
- 2Python面试题面经_python面经
- 3Pytorch学习笔记(二)使用Pytorch的常见错误汇总_[py[y=[[=gp0;=[hp'h=[;t5]t][t'[r'tp--oltpokplk,,vc
- 4MySQL之自带四库之information_schema库_informationschema库
- 5python内置函数map()的应用详解(个人笔记)
- 6抱抱脸(hugging face)教程-中文翻译-模型概要
- 7FAST-LIO论文阅读_fastlio论文
- 8navicat for MySQL的注册方法(windows10)
- 9[运动规划算法]基于硬约束和软约束的轨迹规划
- 10Helsinki-NLP/opus-mt-en-zh 带占位符翻译
三维高斯溅射的精确松弛约束
赞
踩
Relaxing Accurate Initialization Constraint for 3D Gaussian Splatting
三维高斯溅射的精确松弛约束
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
Jiwon Kang
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
Abstract 摘要 Relaxing Accurate Initialization Constraint for 3D Gaussian Splatting
3D Gaussian splatting (3DGS) has recently demonstrated impressive capabilities in real-time novel view synthesis and 3D reconstruction. However, 3DGS heavily depends on the accurate initialization derived from Structure-from-Motion (SfM) methods. When trained with randomly initialized point clouds, 3DGS often fails to maintain its ability to produce high-quality images, undergoing large performance drops of 4-5 dB in PSNR in general. Through extensive analysis of SfM initialization in the frequency domain and analysis of a 1D regression task with multiple 1D Gaussians, we propose a novel optimization strategy dubbed RAIN-GS (Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting) that successfully trains 3D Gaussians from randomly initialized point clouds. We show the effectiveness of our strategy through quantitative and qualitative comparisons on standard datasets, largely improving the performance in all settings.
3D高斯溅射(3DGS)最近表现出令人印象深刻的能力,在实时新颖的视图合成和三维重建。然而,3DGS在很大程度上依赖于从运动恢复结构(SfM)方法得到的精确初始化。当使用随机初始化的点云进行训练时,3DGS通常无法保持其产生高质量图像的能力,通常会在PSNR中经历4-5 dB的大性能下降。通过对频域中SfM初始化的广泛分析以及对具有多个1D高斯的1D回归任务的分析,我们提出了一种名为RAIN-GS(Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting)的新型优化策略,该策略成功地从随机初始化的点云中训练3D高斯。我们通过对标准数据集的定量和定性比较来展示我们策略的有效性,大大提高了所有设置中的性能。
†
![[Uncaptioned image]](https://img-blog.csdnimg.cn/img_convert/cf3e2274ed7a0d5064b97acc6136fdd1.png)
: Equal contribution. 平等贡献。

Figure 1:Effectiveness of our simple strategy. Left and right show the results from 3DGS [13] trained with dense-small-variance (DSV) random initialization (random initialization method used in the original 3DGS) and 3DGS trained with ours, respectively. Transition from 3DGS to ours simply requires sparse-large-variance (SLV) random initialization and progressive Gaussian low-pass filtering. Remarkably, each of our strategies can be implemented with a simple change in one line of code.
图一:我们简单策略的有效性。左和右分别显示了使用密集小方差(DSV)随机初始化(原始3DGS中使用的随机初始化方法)训练的3DGS [ 13]和使用我们的训练的3DGS的结果。从3DGS到我们的转换只需要稀疏大方差(SLV)随机初始化和渐进高斯低通滤波。值得注意的是,我们的每一个策略都可以通过一行代码中的简单更改来实现。
1Introduction 一、导言
Novel view synthesis is one of the essential tasks in computer vision and computer graphics, aiming to render novel views of a 3D scene given a set of images. It has a wide range of applications in various fields, including augmented reality and virtual reality [35], robotics [1], and data generation [8]. Neural radiance fields (NeRFs) [21] have demonstrated remarkable success in this field, learning implicit representations that capture intricate 3D geometry and specular effects solely from images. However, NeRFs’ reliance on multi-layer perceptrons (MLPs) [7, 19, 41, 27, 31] results in slow and computationally intensive volume rendering, hindering real-time applications.
新视图合成是计算机视觉和计算机图形学中的一项重要任务,其目的是在给定的一组图像中绘制三维场景的新视图。它在各个领域都有广泛的应用,包括增强现实和虚拟现实[ 35],机器人[ 1]和数据生成[ 8]。神经辐射场(NeRFs)[ 21]在这一领域取得了显着的成功,学习隐式表示,仅从图像中捕获复杂的3D几何形状和镜面效果。然而,NeRF对多层感知器(MLP)的依赖[ 7,19,41,27,31]导致缓慢且计算密集的体绘制,阻碍了实时应用。
Recently, 3D Gaussian splatting (3DGS) [13] has emerged as a compelling alternative for both high-quality results and real-time rendering. Unlike NeRFs’ implicit representations, 3DGS models the scene using explicit 3D Gaussians. In addition, an efficient CUDA-based differentiable tile rasterization [15, 13] technique enables the rendering of the learned 3D Gaussians in real-time.
最近,3D高斯溅射(3DGS)[13]已经成为高质量结果和实时渲染的一个引人注目的替代方案。与NeRF的隐式表示不同,3DGS使用显式3D高斯模型对场景进行建模。此外,一种有效的基于CUDA的可微分瓦片光栅化[15,13]技术能够实时渲染学习的3D高斯。
Despite its remarkable results, 3DGS exhibits a significant performance drop when trained with randomly initialized point clouds instead of those achieved from Structure-from-Motion (SfM) [13]. This limitation becomes particularly pronounced in scenarios where SfM techniques struggle to converge, such as scenes with symmetry, specular properties, and textureless regions, and limited available views. Also, due to the dependency of 3DGS on initial point clouds, SfM becomes a hard prerequisite even for situations where camera poses can be obtained through external sensors or pre-calibrated cameras [30, 9].
尽管结果显著,但3DGS在使用随机初始化的点云而不是从运动恢复结构(SfM)[13]中获得的点云进行训练时表现出显著的性能下降。这种限制在SfM技术难以收敛的场景中变得特别明显,例如具有对称性、镜面反射属性和无纹理区域以及有限的可用视图的场景。此外,由于3DGS对初始点云的依赖性,即使对于可以通过外部传感器或预校准相机获得相机姿势的情况,SfM也成为一个硬性先决条件[30,9]。
In this work, we start with a natural question: “Why is the initial point cloud so important in 3D Gaussian splatting?” and analyze the difference between SfM and randomly-initialized point clouds. First of all, we analyze the signals in the frequency domain on rendered images and find that SfM initialization can be interpreted as starting with a coarse approximation of the true distribution. In 3DGS, this coarse approximation acts as a foundation for subsequent refinement throughout the optimization process, preventing Gaussians from falling into local minima.
在这项工作中,我们从一个自然的问题开始:“为什么初始点云在3D高斯溅射中如此重要?”并分析了SfM与随机初始化点云的差异。首先,我们分析了渲染图像上频域中的信号,发现SfM初始化可以被解释为从真实分布的粗略近似开始。在3DGS中,这种粗略的近似作为整个优化过程中后续细化的基础,防止高斯陷入局部最小值。
Stemming from this analysis, we conduct a toy experiment of a simplified 1D regression task, to identify the essential elements to guide the Gaussians to robustly learn the ground truth distribution from scratch. This experiment reveals that initially learning the coarse approximation (low-frequency components) of the true distribution is crucial for successful reconstruction. Similar to the SfM initialization, we find the initially learned coarse approximation acts as a guidance when learning the high-frequency components of the distribution.
从这个分析出发,我们进行了一个简化的一维回归任务的玩具实验,以确定基本元素来指导高斯函数从头开始鲁棒地学习地面真值分布。该实验表明,最初学习真实分布的粗略近似(低频分量)对于成功重建至关重要。与SfM初始化类似,我们发现最初学习的粗略近似在学习分布的高频分量时起指导作用。
Expanding upon this observation, we propose a novel optimization strategy, dubbed RAIN-GS (Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting), which combines 1) a novel initialization method of starting with sparse Gaussians with large variance and 2) progressive Gaussian low-pass filtering in the rendering process. Aligned with our observation, we demonstrate that our strategy successfully guides 3D Gaussians to learn the coarse distribution first and robustly learn the remaining high-frequency components later. We show that this simple yet effective strategy largely improves the results when starting from randomly initialized point clouds without any regularization, training, or external models, effectively relaxing the requirement of accurately initialized point clouds from SfM.
在此基础上,我们提出了一种新的优化策略,称为RAIN-GS(Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting),它结合了1)一种新的初始化方法,从具有大方差的稀疏高斯开始,2)渲染过程中的渐进高斯低通滤波。与我们的观察相一致,我们证明了我们的策略成功地引导3D高斯首先学习粗分布,然后鲁棒地学习剩余的高频分量。我们表明,这种简单而有效的策略在从随机初始化的点云开始时,在没有任何正则化,训练或外部模型的情况下,大大改善了结果,有效地放松了对SfM精确初始化点云的要求。
2Related work 2相关工作
2.0.1Novel view synthesis.
2.0.1新颖的视图合成。
Synthesizing images from novel viewpoints of a 3D scene given images captured from multiple viewpoints is one of the essential but challenging tasks in computer vision. Neural radiance fields (NeRF) [21] have succeeded in significantly boosting the performance of this task by optimizing an MLP that can estimate the density and radiance of any continuous 3D coordinate. With the camera poses of the given images, NeRF learns the MLP by querying dense points along randomly selected rays, that outputs the density and color of each of the queried coordinates. Due to the impressive ability to understand and model complex 3D scenes, various follow-ups [3, 4, 5, 11, 17, 22, 29, 36] adopted NeRF as their baseline model and further extend the ability of NeRF to model unbounded or dynamic scenes [3, 4, 17], lower the required number of images for successful training [29, 36], learn a generalizable prior to resolve the need of per-scene optimization [5, 11], or utilize an external hash-grid to fasten the overall optimization process [22]. Although all of these works show compelling results, the volume rendering from dense points along multiple rays makes NeRF hard to apply in real-time settings achieving lower rendering rates of < 1 fps.
在计算机视觉中,从多个视点捕获的图像中合成来自3D场景的新视点的图像是必不可少但具有挑战性的任务之一。神经辐射场(NeRF)[ 21]通过优化可以估计任何连续3D坐标的密度和辐射的MLP,成功地显著提高了这项任务的性能。通过给定图像的相机姿态,NeRF通过查询随机选择的射线沿着的密集点来学习MLP,输出每个查询坐标的密度和颜色。 由于理解和建模复杂3D场景的能力令人印象深刻,各种后续[3,4,5,11,17,22,29,36]采用NeRF作为其基线模型,并进一步扩展NeRF建模无界或动态场景的能力[3,4,17],降低成功训练所需的图像数量[29,36],在解决每个场景优化的需求之前学习泛化[5,11],或者利用外部哈希网格来加快整体优化过程[ 22]。虽然所有这些工作都显示出令人信服的结果,但从密集点沿沿着多条射线进行体绘制使得NeRF难以应用于实时设置,从而实现< 1 fps的较低绘制速率。
Recently, 3D Gaussian splatting (3DGS) [13] has emerged as a promising alternative, succeeding in high-quality real-time novel-view synthesis at 1080p resolution with frame rates exceeding 90 fps. 3DGS achieves this by modeling the 3D scene with explicit 3D Gaussians, followed by an efficient and differentiable tile rasterization implemented in CUDA to accelerate the rendering process. Due to the efficient and fast architecture of 3DGS, it gained massive attention from various fields [33, 38, 20, 37], extended to model dynamic scenes [37, 20], or used as an alternative for text-to-3D tasks [33, 38] for fast generation. Nevertheless, the essential requirement of both accurate pose and initial point clouds limits the application of 3DGS to only scenes where SfM is applicable. In this work, we analyze the optimization strategy of 3DGS and present a simple yet effective change in the optimization strategy to expand the versatility of 3DGS to successfully learn the scene without accurate initialization.
最近,3D高斯溅射(3DGS)[ 13]已经成为一个有前途的替代方案,成功地在1080p分辨率下以超过90 fps的帧速率进行高质量的实时新颖视图合成。3DGS通过使用显式3D高斯模型对3D场景进行建模来实现这一点,然后在CUDA中实现高效且可区分的瓦片光栅化以加速渲染过程。由于3DGS的高效和快速架构,它获得了各个领域的大量关注[33,38,20,37],扩展到模型动态场景[37,20],或用作文本到3D任务的替代方案[33,38]以快速生成。然而,准确的姿态和初始点云的基本要求限制了3DGS的应用,只有场景中的SfM是适用的。 在这项工作中,我们分析了3DGS的优化策略,并提出了一个简单而有效的优化策略的变化,以扩大3DGS的通用性,成功地学习场景,而无需准确的初始化。
2.0.2Structure-from-Motion (SfM).
2.0.2运动恢复结构(SfM)。
SfM techniques [2, 6, 28] have been one of the most widely used algorithms to reconstruct a 3D scene. Typical SfM methods output the pose of each input image and a sparse point cloud that includes rough color and position information for each point. These methods employ feature extraction, matching steps, and bundle adjustment. For the task of novel view synthesis, NeRF [21] utilizes the estimated pose from the SfM and trains an implicit representation to model the scene. The recently proposed 3DGS [13] utilizes both the accurate pose and initial point cloud as an initialization for the position and color of 3D Gaussians, showing large performance drops when this initialization is not accessible.
SfM技术[2,6,28]已经是用于重建3D场景的最广泛使用的算法之一。典型的SfM方法输出每个输入图像的姿态和包括每个点的粗略颜色和位置信息的稀疏点云。这些方法采用特征提取、匹配步骤和光束法平差。对于新视图合成的任务,NeRF [ 21]利用来自SfM的估计姿态并训练隐式表示来对场景进行建模。最近提出的3DGS [ 13]利用准确的姿势和初始点云作为3D高斯的位置和颜色的初始化,当无法访问此初始化时,显示出较大的性能下降。
Despite the effectiveness of SfM in generating accurately aligned point clouds and precise camera poses, its incremental nature and the computational intensity of the bundle adjustment process significantly increase its time complexity, often to �(�4) with respect to � cameras involved [34]. Due to the high computational demand, SfM being a hard prerequisite limits the feasibility of NeRF or 3DGS for scenarios that require real-time processing. In addition, SfM often struggles to converge, such as in scenes with symmetry, specular properties, and textureless regions, and when the available views are limited.
尽管SfM在生成精确对齐的点云和精确的相机姿态方面是有效的,但其增量性质和光束法平差过程的计算强度显著增加了其时间复杂度,相对于所涉及的 � 相机,通常增加到 �(�4) [ 34]。由于高计算需求,SfM是一个硬性先决条件,限制了NeRF或3DGS在需要实时处理的场景中的可行性。此外,SfM通常难以收敛,例如在具有对称性、镜面反射属性和无纹理区域的场景中,以及当可用视图有限时。
3Preliminary: 3D Gaussian splatting (3DGS)
3初步:三维高斯溅射(3DGS)
Recently, 3DGS [13] has emerged as a promising alternative for the novel view synthesis task, modeling the scene with multiple 3D Gaussians [42]. Each �-th Gaussians �� represents the scene with the following attributes: a position vector ��∈ℝ3, an anisotropic covariance matrix Σ�∈ℝ3×3, spherical harmonic (SH) coefficients [39, 22], and an opacity logit value ��∈[0,1). With these attributes, each Gaussian �� is defined in the world space [42] as follows:
最近,3DGS [ 13]已经成为新视图合成任务的一个有前途的替代方案,使用多个3D高斯模型对场景进行建模[ 42]。每个第 � 个高斯项 �� 表示具有以下属性的场景:位置向量 ��∈ℝ3 、各向异性协方差矩阵 Σ�∈ℝ3×3 、球谐(SH)系数[ 39,22]和不透明度logit值 ��∈[0,1) 。有了这些属性,每个高斯 �� 在世界空间中定义如下:
| ��(�)=�−12(�−��)�Σ�−1(�−��). | (1) |
To render an image from a pose represented by the viewing transformation �, the projected covariance Σ�′ is defined as follows:
为了从由观看变换 � 表示的姿态渲染图像,如下定义投影协方差 Σ�′ :
| Σ�′=��Σ�����, | (2) |
where � is the Jacobian of the local affine approximation of the projective transformation. The 2D covariance matrix is simply obtained by skipping the third row and column of Σ�′ [42]. Finally, to render the color �(�) of the pixel �, 3DGS utilizes alpha blending according to the Gaussians depth. For example, when � Gaussians are sorted by depth, the color �(�) is calculated as follows:
其中 � 是投影变换的局部仿射近似的雅可比矩阵。通过跳过 Σ�′ [ 42]的第三行和第三列来简单地获得2D协方差矩阵。最后,为了渲染像素 � 的颜色 �(�) ,3DGS根据高斯深度利用阿尔法混合。例如,当 � 高斯按深度排序时,颜色 �(�) 计算如下:
| �(�)=∑�=1�������′(�)∏�=1�−1(1−����′(�)), | (3) |
where �� is the view-dependent color value of each Gaussian calculated with the SH coefficients, and ��′ is the 3D Gaussian projected to the 2D screen space.
其中 �� 是利用SH系数计算的每个高斯的视图相关颜色值,并且 ��′ 是投影到2D屏幕空间的3D高斯。
Since 3DGS starts learning from sparse point clouds, they utilize an adaptive density control to obtain a more accurate and denser representation. By considering if the scene is under-/over-constructed, the Gaussian undergoes a clone/split operation to represent the scene with an adequate number of Gaussians.
由于3DGS从稀疏点云开始学习,因此它们利用自适应密度控制来获得更准确和更密集的表示。通过考虑场景是否构造不足/过度,高斯经历克隆/分裂操作以用足够数量的高斯来表示场景。
4Motivation 4动机

Figure 2:Analysis of SfM initialization in 3DGS. (a) The top shows the GT image, and the bottom is the rendered image by 3DGS after only 10 steps with SfM initialization. We can observe that the rendered image is already coarsely-close to GT image. To analyze the images in the frequency domain, we randomly sample a horizontal line from the image marked in red. (b) The pixel intensity values along this line are shown, with the GT image indicated in orange and the rendered image in blue. (c) This graph visualizes the magnitude of the frequency components of (b). Since frequencies further from the middle of the x-axis represent high-frequency components, we observe that SfM provides coarse approximation of the true distribution.
图2:3DGS中SfM初始化的分析。(a)顶部显示GT图像,底部是使用SfM初始化仅10个步骤后由3DGS渲染的图像。我们可以观察到渲染图像已经粗略地接近GT图像。为了在频域中分析图像,我们从红色标记的图像中随机抽取一条水平线。(b)显示了沿这条线的像素强度值沿着,GT图像以橙子表示,渲染图像以蓝色表示。(c)该图可视化了(B)的频率分量的幅度。由于距离x轴中间较远的频率表示高频分量,我们观察到SfM提供了真实分布的粗略近似。
4.1SfM initialization in 3DGS
4.1 3DGS中的SfM初始化
To understand the large performance gap of 3DGS [13] depending on different initialization of point clouds, we first analyze its behavior when trained using an SfM point cloud. As explained in Section 2, SfM provides a sparse point cloud with rough information of color and position. 3DGS effectively leverages this output, initializing the Gaussian parameters �� and spherical harmonic (SH) coefficients to the position of the point clouds and estimated color. This initialization’s advantage is evident in Figure 2 (bottom row, (a)): after only 10 steps (0.03% of the total training steps), the rendered result already exhibits reasonable quality and similarity to the true image (top row, (a)).
为了理解3DGS [ 13]的巨大性能差距取决于点云的不同初始化,我们首先分析了使用SfM点云训练时的行为。如第2节所述,SfM提供了具有颜色和位置的粗略信息的稀疏点云。3DGS有效地利用该输出,将高斯参数 �� 和球谐(SH)系数初始化为点云的位置和估计的颜色。这种初始化的优点在图2(底行,(a))中是明显的:仅在10个步骤(总训练步骤的0.03 % )之后,渲染结果已经表现出合理的质量和与真实图像的相似性(顶行,(a))。
To further investigate the benefits of SfM initialization, we analyze the rendered images in the frequency domain using Fourier transform [24]. In Figure 2, we randomly select a horizontal line from both the ground-truth and rendered images as shown in red in (a). The pixel intensity values along this line are visualized in (b), with the ground-truth image in orange and the rendered image in blue. These signals are then transformed into the frequency domain and presented in (c). This analysis in the frequency domain demonstrates that SfM initialization provides a coarse approximation of the underlying distribution.
为了进一步研究SfM初始化的好处,我们使用傅立叶变换[ 24]在频域中分析渲染图像。在图2中,我们从地面实况和渲染图像中随机选择一条水平线,如(a)中的红色所示。沿着这条线的像素强度值沿着在(B)中可视化,其中地面实况图像为橙子,渲染图像为蓝色。然后将这些信号变换到频域并在(c)中呈现。在频域中的这种分析表明,SfM初始化提供了基本分布的粗略近似。
As the goal of novel view synthesis is to understand the 3D distribution of the scene, it is necessary to model both low- and high-frequency components of the true distribution. To enable this, NeRF [21, 32] utilizes positional encoding to facilitate learning of high-frequency components. However, the over-fast convergence of high-frequency components hinders NeRF from exploring low-frequency components, leading NeRF to overfit to high-frequency artifcats [36]. To circumvent this problem, prior works [36, 25, 18] adopt a frequency annealing strategy, guiding NeRF to sufficiently explore the low-frequency components first.
由于新视图合成的目标是了解场景的3D分布,因此有必要对真实分布的低频和高频分量进行建模。为了实现这一点,NeRF [ 21,32]利用位置编码来促进高频分量的学习。然而,高频分量的过快收敛阻碍了NeRF探索低频分量,导致NeRF过度拟合高频人工信号[ 36]。为了避免这个问题,先前的工作[36,25,18]采用频率退火策略,引导NeRF首先充分探索低频分量。
In this perspective, starting from SfM initialization can be understood as following a similar process, as it already provides the low-frequency components (Figure 2). Expanding upon this analysis, we propose that a similar strategy that can guide 3DGS to learn the low-frequency component first is essential to enable robust training when starting with randomly initialized point clouds.
从这个角度来看,从SfM初始化开始可以理解为遵循类似的过程,因为它已经提供了低频分量(图2)。在此分析的基础上,我们提出了一种类似的策略,可以引导3DGS首先学习低频分量,这对于从随机初始化的点云开始进行鲁棒训练至关重要。

Figure 3:Toy experiment to analyze different initialization methods. This figure visualizes the result of our toy experiment predicting the target distribution using a collection of 1D Gaussians, starting from different initialization methods. Dense-small-variance (DSV) and dense-large-variance (DLV) initialize 1,000 1D Gaussians, where DLV is initialized with large variances by adding � to the initial variance. Small-large-variance (SLV) initializes 15 1D Guassians with the same � added to the initial variance. We can observe the over-fast convergence of high-frequency components on DSV initialization, which is resolved in the DLV initialization but fails to converge due to fluctuation. SLV initialization resolves both problems, learning the low-frequency components first and also converging to successfully model the target distribution.
图3:分析不同初始化方法的玩具实验。该图可视化了我们的玩具实验的结果,该实验使用1D高斯集合从不同的初始化方法开始预测目标分布。密集小方差(DSV)和密集大方差(DLV)初始化1,000个一维高斯,其中DLV通过将 � 添加到初始方差来初始化为大方差。小-大-方差(SLV)1015一维高斯,将相同的 � 添加到初始方差中。我们可以观察到DSV初始化时高频分量的过快收敛,这在DLV初始化中得到解决,但由于波动而无法收敛。SLV初始化解决了这两个问题,首先学习低频分量,然后收敛以成功地模拟目标分布。
4.2Dense random initialization in 3DGS
4.2 3DGS中的密集随机初始化
For situations where initialized point clouds from SfM are unavailable, [13] proposes a dense-small-variance (DSV) random initialization method. They randomly sample dense point clouds within a cube three times the size of the camera’s bounding box. As the initial covariance is defined as the mean distance to the three nearest neighboring points, this leads to initializing dense 3D Gaussians with small variances.
对于SfM初始化点云不可用的情况,[ 13]提出了一种密集小方差(DSV)随机初始化方法。他们在一个三倍于相机边界框大小的立方体内随机采样密集的点云。由于初始协方差被定义为到三个最近相邻点的平均距离,这导致初始化具有小方差的密集3D高斯。
Building upon the importance of prioritizing low-frequency learning, we conduct a toy experiment in a simplified 1D regression task to examine how DSV initialization influences the optimization process. Using 1D Gaussians provides a controlled environment isolating the effects of initialization. Specifically, we define 1D Gaussians with its mean �� and variance ��2 as learnable parameters to model a random 1D signal �(�) as the ground truth distribution. By blending the � Gaussians with a learnable weight ��, we train the parameters with the L1 loss between the blended signal and �(�) as follows:
基于优先考虑低频学习的重要性,我们在简化的1D回归任务中进行了一个玩具实验,以研究DSV初始化如何影响优化过程。使用1D Gaussians提供了一个隔离初始化影响的受控环境。具体来说,我们定义1D高斯,其均值 �� 和方差 ��2 作为可学习参数,以将随机1D信号 �(�) 建模为地面真实分布。通过将 � 高斯函数与可学习权重 �� 混合,我们使用混合信号和 �(�) 之间的L1损失来训练参数,如下所示:
| ℒ=∑�∥�(�)−∑�=0���⋅exp(−(�−��)22��2)∥, | (4) |
where we set �=1,000 for the DSV initialization setting.
其中,我们将 �=1,000 设置为DSV初始化设置。
As shown in the top row of Figure 3, training with the DSV random initialization exhibits a tendency towards over-fast convergence on high frequencies. This is evident in the model’s ability to capture high-frequency components after only 10 steps. However, this rapid focus on high-frequencies leads to undesired high-frequency artifacts in the final reconstruction (zoomed-in box at 1,000 steps). We hypothesize that this behavior arises from the small initial variances of the dense Gaussians, which restrict each Gaussian to model a very localized region, increasing the susceptibility to overfitting.
如图3的顶行所示,使用DSV随机初始化的训练表现出在高频上过快收敛的趋势。这一点在该模型仅10步后就能捕获高频分量的能力中显而易见。然而,这种对高频的快速聚焦导致最终重建中的不期望的高频伪影(在1,000步处放大框)。我们假设,这种行为是由于密集高斯的初始方差很小,这限制了每个高斯模型一个非常局部的区域,增加了过拟合的敏感性。
To verify our hypothesis, we repeat the experiment with a value � added to the initial variance changing our initialization to dense-large-variance (DLV). Note that this modification effectively encourages the Gaussians to learn from wider areas. The results (middle row of Figure 3) support our hypothesis: the learned signal at 10 steps demonstrates a prioritization of low-frequency components when compared to DSV initialization. However, even with the ability to prune Gaussians by learning weights as ��=0, the dense initialization causes fluctuations in the learned signal, preventing convergence after 1,000 steps. These observations highlight a crucial point: while learning from wider areas (enabled by a large variance) is necessary to prioritize low-frequency components, a dense initialization can still lead to instability and convergence issues. More detailed settings and results of the toy experiment are provided in Section C in the supplementatry materials.
为了验证我们的假设,我们重复实验,将值 � 添加到初始方差,将初始化更改为密集大方差(DLV)。请注意,这种修改有效地鼓励高斯从更广泛的领域学习。结果(图3的中间行)支持我们的假设:与DSV初始化相比,10步处的学习信号表明低频分量的优先级。然而,即使具有通过学习权重来修剪高斯的能力,如 ��=0 ,密集初始化也会导致学习信号的波动,从而防止1,000步后的收敛。这些观察结果突出了一个关键点:虽然从更广泛的领域(由大的方差实现)学习对于优先考虑低频分量是必要的,但密集的初始化仍然可能导致不稳定和收敛问题。更详细的设置和结果的玩具实验中提供的第C节的实验材料。
5Methodology 5方法学
Following our motivation (Section 4), we propose a novel optimization strategy, dubbed RAIN-GS (Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting). This strategy guides 3D Gaussians towards prioritizing the learning of low-frequency components during the early phases of training, which enables the robust training of the remaining high-frequency components without falling into local minima. Our strategy consists of two key components: 1) sparse-large-variance (SLV) initialization (Section 5.1) and 2) progressive Gaussian low-pass filtering (Section 5.2).
根据我们的动机(第4节),我们提出了一种新的优化策略,称为RAIN-GS(Relaxing Accurate Initialization Constraint for 3D Gaussian Splatting)。该策略指导3D高斯在训练的早期阶段优先学习低频分量,这使得剩余高频分量的鲁棒训练不会陷入局部最小值。我们的策略包括两个关键部分:1)稀疏大方差(SLV)初始化(第5.1节)和2)渐进高斯低通滤波(第5.2节)。
5.1Sparse-large-variance (SLV) initialization
5.1稀疏大方差初始化
As demonstrated in the 1D toy experiment (Section 4.2), optimization from a dense initialization fails to faithfully model the target distribution, where DLV produces undesired high-frequency artifacts and DSV fails to converge although succeeding in learning the low-frequency components first.
如1D玩具实验(第4.2节)所示,密集初始化的优化无法忠实地对目标分布进行建模,其中DLV产生不希望的高频伪影,DSV无法收敛,尽管它首先成功学习了低频分量。
To resolve both problems, we propose a sparse-large-variance (SLV) initialization. The sparsity reduces fluctuations throughout the optimization, while the large variance ensures initial focus on the low-frequency distribution. This is demonstrated in the bottom row of Figure 3, where the experiment is repeated with �=15 Gaussians with � added to the initial variance. SLV initialization succeeds in both the prioritization of low-frequency components at 10 steps and the modeling of the true distribution with minimal errors after 1,000 steps.
为了解决这两个问题,我们提出了一个稀疏大方差(SLV)初始化。稀疏性减少了整个优化过程中的波动,而大的方差确保了对低频分布的初始关注。这在图3的底行中证明,其中使用 �=15 高斯重复实验,其中将 � 添加到初始方差。SLV初始化成功地在10个步骤中对低频分量进行了优先级排序,并在1,000个步骤后以最小的误差对真实分布进行了建模。
Therefore, although initializing random points from the same volume which is defined as three times the size of the camera’s bounding box, we initialize a significantly sparser set of 3D Gaussians. As the initial covariance of 3D Gaussian is defined based on the distances of the three nearest neighbors, sparse initialization leads to a larger initial covariance, encouraging each Gaussian to model a wider region of the scene.
因此,虽然初始化的随机点从相同的体积被定义为相机的边界框的大小的三倍,我们初始化一个显着稀疏的3D高斯集。由于3D高斯的初始协方差是基于三个最近邻居的距离定义的,因此稀疏初始化会导致更大的初始协方差,从而鼓励每个高斯对场景的更宽区域进行建模。
When initializing � points, DSV initialization from [13] originally chooses �>100K. Aligned with our analysis, lowering this value significantly improves performance by encouraging the initial focus on low-frequency components, producing fewer high-frequency artifacts. Surprisingly, this strategy becomes more effective even with extremely sparse initializations (e.g., as low as �=10), verifying the effectiveness of our novel SLV initialization method. An illustration of different initialization methods is shown in Figure 4.
初始化 � 点时,[ 13]中的DSV初始化最初选择 �>100 K。与我们的分析一致,降低此值可以通过鼓励初始关注低频分量来显著提高性能,从而减少高频伪影。令人惊讶的是,这种策略甚至在极其稀疏的初始化(例如,低至 �=10 ),验证了本文提出的SLV初始化方法的有效性。不同初始化方法的说明如图4所示。

Figure 4:Visualization of different initialization methods. This figure illustrates the effect of different initialization methods. (a) Ground truth image. (b) Initialized point cloud from Structure-from-Motion (SfM). (c) Dense-small-variance (DSV) random initialization with small initial covariances due to the short distance between Gaussians. (d) Sparse-large-variance (SLV) random initialization with large initial covariances due to wider distance between Gaussians.
图4:不同初始化方法的可视化。此图说明了不同初始化方法的效果。(a)地面实况图像。(b)从运动恢复结构(SfM)初始化点云。(c)密集小方差(DSV)随机初始化,由于高斯之间的距离很短,初始协方差很小。(d)稀疏大方差(SLV)随机初始化,由于高斯之间的距离较宽,初始协方差较大。
5.2Progressive Gaussian low-pass filter control
5.2渐进高斯低通滤波器控制
Although our SLV initialization method is effective, we find that after multiple densification steps the number of 3D Gaussians increases exponentially, showing a tendency to collapse into similar problems with the DSV initialization. To regularize the 3D Gaussians to sufficiently explore the low-frequency components during the early stage of training, we propose a novel progressive control of the Gaussian low-pass filter utilized in the rendering stage.
虽然我们的SLV初始化方法是有效的,我们发现,经过多个致密化步骤的3D高斯的数量呈指数级增加,显示出崩溃成类似的问题与DSV初始化的趋势。为了在训练的早期阶段对3D高斯进行正则化以充分探索低频分量,我们提出了一种新的渐进控制在渲染阶段使用的高斯低通滤波器。
Specifically, in the rendering stage of 3DGS, the 2D Gaussian ��′ projected from a 3D Gaussian �� is defined as follows:
具体地,在3DGS的渲染阶段,从3D高斯 �� 投影的2D高斯 ��′ 定义如下:
| ��′(�)=�−12(�−��′)�Σ�′−1(�−��′). | (5) |
However, directly using projected 2D Gaussians can lead to visual artifacts when they become smaller than a pixel [13, 40]. To ensure coverage of at least one pixel, 13 enlarge the 2D Gaussian’s scale by adding a small value to the covariance’s diagonal elements as follows:
然而,直接使用投影的2D高斯可能会导致视觉伪影,当它们变得小于像素时[ 13,40]。为了确保覆盖至少一个像素,13通过向协方差的对角元素添加一个小值来扩大2D高斯尺度,如下所示:
| ��′(�)=�−12(�−��′)�(Σ�′+��)−1(�−��′), | (6) |
where � is a pre-defined value of �=0.3 and � is an identity matrix. This process can also be interpreted as the convolution between the projected 2D Gaussian ��′ and a Gaussian low-pass filter ℎ (mean �=0 and variance �2=0.3) of ��′⊗ℎ, which is shown to be an essential step to prevent aliasing [42]. After convolution with the low-pass filter, the area of the projected Gaussian ��′ is approximated by a circle with a radius defined by three times the larger eigenvalue of the 2D covariance matrix (Σ�′+��).
其中 � 是 �=0.3 的预定义值,并且 � 是单位矩阵。该过程也可以被解释为投影的2D高斯 ��′ 和 ��′⊗ℎ 的高斯低通滤波器 ℎ (平均值 �=0 和方差 �2=0.3 )之间的卷积,这被示出为防止混叠的必要步骤[ 42]。在与低通滤波器卷积之后,投影高斯 ��′ 的区域由半径由2D协方差矩阵 (Σ�′+��) 的较大特征值的三倍定义的圆近似。11We provide a detailed proof in Section 0.B.1 in the Appendix.
我们在附录第0.B.1节中提供了详细的证明。 Figure 5 illustrates the low-pass filter’s effect, where the projected Gaussian is splatted to wider areas in (b) compared to (a).
图5说明了低通滤波器的效果,其中与(a)相比,(B)中投影的高斯分布被溅射到更宽的区域。
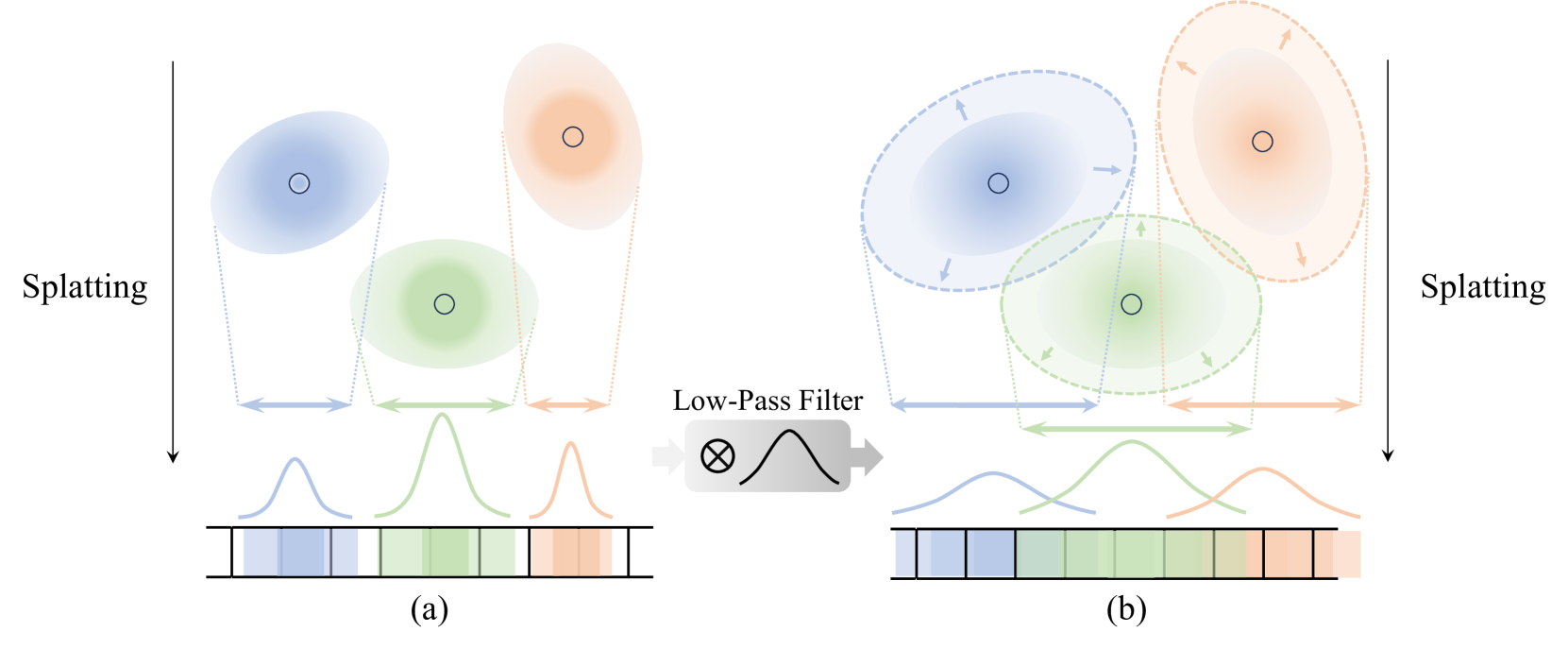
Figure 5:Visualization of low-pass filter. This figure shows the visualization of the effect of the low-pass filter. As shown in (b), the convolution of the splatted 2D Gaussian with the low-pass filter expands the area the Gaussian is splatted onto, resulting in the Gaussians affecting larger areas than naïve splatting as shown in (a).
图5:低通滤波器的可视化。该图显示了低通滤波器效果的可视化。如(B)所示,溅射的2D高斯与低通滤波器的卷积扩展了高斯被溅射到的区域,导致高斯影响比(a)所示的朴素溅射更大的区域。
In our approach, instead of using a fixed value of � through the entire optimization process, we notice that this value � can ensure the minimum area each Gaussians have to cover in the screen space. Based on our analysis in Section 4.2 that learning from wider areas prioritizes low-frequency components, we control � to regularize the Gaussians to cover wide areas during the early stage of training and progressively learn from a more local region. Specifically, as the value � ensures the projected Gaussians area to be larger than 9��, we define the value � such that �=��/9��, where � indicates the number of Gaussians, which may vary across evolving iterations, and �,� indicates the height and width of the image respectively.22We provide a detailed proof in Section 0.B.2 in the Appendix.
我们在附录第0.B.2节中提供了详细的证明。
在我们的方法中,在整个优化过程中,我们没有使用固定值 � ,而是注意到这个值 � 可以确保每个高斯函数在屏幕空间中必须覆盖的最小区域。基于我们在第4.2节中的分析,即从更广泛的区域学习优先考虑低频分量,我们控制 � 以在训练的早期阶段将高斯正则化以覆盖更广泛的区域,并逐步从更局部的区域学习。具体地,由于值 � 确保投影的高斯区域大于 9�� ,所以我们定义值 � 使得 �=��/9�� ,其中 � 指示高斯的数量,其可以在演进迭代中变化,并且 �,� 分别指示图像的高度和宽度。 2 It should be noted that although the number of Gaussians may fluctuate across evolving iterations, we name our strategy as progressive Gaussian low-pass filter control due to the tendency of Gaussians to increase exponentially. We find utilizing both the SLV random initialization and the progressive low-pass filter control is crucial to robustly guide the 3D Gaussians to learn the low-frequency first.
应该注意的是,虽然高斯的数量可能会在不断变化的迭代中波动,但由于高斯的指数增长趋势,我们将我们的策略命名为渐进高斯低通滤波器控制。我们发现利用SLV随机初始化和渐进低通滤波器控制是至关重要的鲁棒性引导三维高斯首先学习低频。
6Experiments 6实验
6.1Datasets
To assess the effectiveness of our strategy, we conduct qualitative and quantitative comparisons using the same datasets previously utilized in the evaluation of the 3DGS method [13]. Specifically, we train our method on the Mip-NeRF360 dataset [4], the Tanks&Temples dataset [14], and the Deep Blending dataset [10]. We evaluate the PSNR, LPIPS, and SSIM metrics by constructing a train/test split using every 8th image for testing, as suggested in Mip-NeRF360 [4]. In terms of image resolution, we follow 3DGS and utilize a pre-downscaled dataset. Specifically, we use 4 times downscaled images for outdoor scenes and 2 times downscaled images for indoor scenes in the Mip-NeRF360 dataset. For the Tanks&Temples and Deep Blending datasets, we use the original images for both training and testing.
为了评估我们的策略的有效性,我们使用先前在3DGS方法评估中使用的相同数据集进行定性和定量比较[ 13]。具体来说,我们在Mip-NeRF 360数据集[ 4],Tanks&Temples数据集[ 14]和Deep Blending数据集[ 10]上训练我们的方法。如Mip-NeRF 360 [ 4]中所建议的,我们通过使用每8张图像构建训练/测试分割来评估PSNR,LPIPS和SSIM指标。在图像分辨率方面,我们遵循3DGS并利用预缩小的数据集。具体来说,我们在Mip-NeRF 360数据集中使用4倍缩小的图像用于室外场景,2倍缩小的图像用于室内场景。对于Tanks&Temples和Deep Blending数据集,我们使用原始图像进行训练和测试。
6.2Implementation details
6.2实现细节
We implement our model based on the 3DGS [13], which consists of the PyTorch framework [26] and CUDA kernels for rasterization [15, 13]. We follow the same training process of the existing implementation in all datasets. For our sparse-large-variance (SLV) random initialization, we set the initial number of Gaussians to �=10 which is empirically found to be robust even for different datasets. For progressive low-pass filter control, we find that re-defining the value � as �=min(max(��/9��,0.3), 300.0) every 1,000 steps results in better results compared to changing the value every step and adopt this strategy as default. For training SH coefficients, we set the maximum degree as 3 following the original implementation. Unlike 13, we start increasing SH degree every 1,000 steps after 5,000 steps as our strategy facilitates the learning of low-frequency components in the early stage of training. Also to prevent Gaussians from rapidly becoming Gaussians with small variances, we lower the divide factor from 1.6 to 1.4. All other hyperparameters are left unchanged.
我们基于3DGS [ 13]实现我们的模型,该模型由PyTorch框架[ 26]和用于光栅化的CUDA内核[ 15,13]组成。我们在所有数据集中遵循与现有实现相同的训练过程。对于我们的稀疏大方差(SLV)随机初始化,我们将高斯的初始数量设置为 �=10 ,根据经验发现即使对于不同的数据集也是鲁棒的。对于渐进式低通滤波器控制,我们发现,与每一步改变值相比,每1,000步将值 � 重新定义为 �=min(max(��/9��,0.3), 300.0) 会产生更好的结果,并将此策略作为默认策略。对于训练SH系数,我们按照原始实现将最大度设置为3。与13不同,我们在5,000步之后每1,000步开始增加SH度,因为我们的策略有助于在训练的早期阶段学习低频成分。同样为了防止高斯分布迅速变成方差很小的高斯分布,我们将除法因子从1降低。6到1.4所有其他超参数保持不变。
Table 1:Quantitative comparison on Mip-NeRF360 dataset. We compare our method with previous approaches, including the random initialization method (DSV) described in the original 3DGS [13]. We report PSNR, SSIM, LPIPS and color each cell as best, second best and third best. †: As 3DGS [13] is the only method that utilizes SfM point clouds, the values are only included for reference.
表1:Mip-NeRF 360数据集的定量比较。我们将我们的方法与以前的方法进行比较,包括原始3DGS [ 13]中描述的随机初始化方法(DSV)。我们报告PSNR,SSIM,LPIPS和颜色每个细胞为最好的,第二好的和第三好的。 † :由于3DGS [ 13]是使用SfM点云的唯一方法,因此仅包括这些值以供参考。
| Outdoor Scene 室外场景 | |||||||||||||||
| Method | bicycle | flowers | garden | stump | treehill | ||||||||||
| PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM ↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM ↑ 阿信 ↑ | LPIPS↓ | |
| 3DGS† | 25.246 | 0.771 | 0.205 | 21.520 | 0.605 | 0.336 | 27.410 | 0.868 | 0.103 | 26.550 | 0.775 | 0.210 | 22.490 | 0.638 | 0.317 |
| Plenoxels | 21.912 | 0.496 | 0.506 | 20.097 | 0.431 | 0.521 | 23.495 | 0.606 | 0.386 | 20.661 | 0.523 | 0.503 | 22.248 | 0.509 | 0.540 |
| INGP-Base | 22.193 | 0.491 | 0.487 | 20.348 | 0.450 | 0.481 | 24.599 | 0.649 | 0.312 | 23.626 | 0.574 | 0.450 | 22.364 | 0.518 | 0.489 |
| INGP-Big | 22.171 | 0.512 | 0.446 | 20.652 | 0.486 | 0.441 | 25.069 | 0.701 | 0.257 | 23.466 | 0.594 | 0.421 | 22.373 | 0.542 | 0.450 |
| 3DGS (DSV) | 21.034 | 0.575 | 0.378 | 17.815 | 0.469 | 0.403 | 23.217 | 0.783 | 0.175 | 20.745 | 0.618 | 0.345 | 18.986 | 0.550 | 0.413 |
| Ours | 23.716 | 0.623 | 0.368 | 20.707 | 0.542 | 0.391 | 26.028 | 0.819 | 0.164 | 24.258 | 0.673 | 0.321 | 21.846 | 0.587 | 0.397 |
| Indoor Scene | |||||||||||||||
| room | counter | kitchen | bonsai | average | |||||||||||
| Method | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM ↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM ↑ 阿信 ↑ | LPIPS↓ |
| 3DGS† | 30.632 | 0.914 | 0.220 | 28.700 | 0.905 | 0.204 | 30.317 | 0.922 | 0.129 | 31.980 | 0.938 | 0.205 | 27.205 | 0.815 | 0.214 |
| Plenoxels | 27.594 | 0.842 | 0.419 | 23.624 | 0.759 | 0.441 | 23.420 | 0.648 | 0.447 | 24.669 | 0.814 | 0.398 | 23.080 | 0.625 | 0.462 |
| INGP-Base | 29.269 | 0.855 | 0.301 | 26.439 | 0.798 | 0.342 | 28.548 | 0.818 | 0.254 | 30.337 | 0.890 | 0.227 | 25.302 | 0.671 | 0.371 |
| INGP-Big | 29.690 | 0.871 | 0.261 | 26.691 | 0.817 | 0.306 | 29.479 | 0.858 | 0.195 | 30.685 | 0.906 | 0.205 | 25.586 | 0.699 | 0.331 |
| 3DGS (DSV) | 29.685 | 0.894 | 0.265 | 23.608 | 0.833 | 0.276 | 26.078 | 0.893 | 0.161 | 18.538 | 0.719 | 0.401 | 22.190 | 0.705 | 0.313 |
| Ours | 30.240 | 0.894 | 0.249 | 27.826 | 0.870 | 0.260 | 30.235 | 0.913 | 0.149 | 30.702 | 0.920 | 0.239 | 26.180 | 0.761 | 0.280 |
Table 2:Quantitative comparison on Tanks&Temples and Deep Blending dataset. We compare our method with previous approaches, including the random initialization method (DSV) described in the original 3DGS [13]. We report PSNR, SSIM, LPIPS and color each cell as best, second best and third best. †: As 3DGS [13] is the only method that utilizes SfM point clouds, the values are only included for reference.
表2:Tanks & Temples和Deep Blending数据集的定量比较。我们将我们的方法与以前的方法进行比较,包括原始3DGS [13]中描述的随机初始化方法(DSV)。我们报告PSNR,SSIM,LPIPS和颜色每个细胞为最好的,第二好的和第三好的。 † :由于3DGS [13]是使用SfM点云的唯一方法,因此仅包括这些值以供参考。
| Tanks&Temples 坦克和寺庙 | Deep Blending 深度交融 | |||||||||||
| Method | Truck | Train | DrJohnson | Playroom | ||||||||
| PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | PSNR↑ PSNR ↑ 的问题 | SSIM ↑ 阿信 ↑ | LPIPS↓ LPIPPS ↓ 的问题 | |
| 3DGS† | 25.187 | 0.879 | 0.148 | 21.097 | 0.802 | 0.128 | 28.766 | 0.899 | 0.244 | 30.044 | 0.906 | 0.241 |
| Plenoxels | 23.221 | 0.774 | 0.335 | 18.927 | 0.663 | 0.422 | 23.142 | 0.787 | 0.521 | 22.980 | 0.802 | 0.465 |
| INGP-Base | 23.260 | 0.779 | 0.274 | 20.170 | 0.666 | 0.386 | 27.750 | 0.839 | 0.381 | 19.483 | 0.754 | 0.465 |
| INGP-Big | 23.383 | 0.800 | 0.249 | 20.456 | 0.689 | 0.360 | 28.257 | 0.854 | 0.352 | 21.665 | 0.779 | 0.428 |
| 3DGS (DSV) | 21,149 | 0.758 | 0.248 | 20.824 | 0.772 | 0.255 | 28.668 | 0.894 | 0.258 | 28.358 | 0.896 | 0.258 |
| Ours | 23.732 | 0.841 | 0.196 | 21.144 | 0.763 | 0.267 | 28.993 | 0.894 | 0.260 | 30.261 | 0.908 | 0.255 |
Figure 6:Qualitative results on Mip-NeRF360 dataset.


