【蓝桥杯 C++高级组省赛以及2020年-蓝桥杯C++省赛合集+部分答案】_蓝桥杯答案

第五题（难度系数 7，满分 100 分）

编程实现： 题目的分数值

程序命名：score.cpp

题目描述:

蓝桥杯 C++青少组的比赛有 n 个问题，现在请你给这 n 个问题分配分值。

n 个问题已经按从简单到困难排好序，第 i 个问题的分值是 A i 。n 个问题的分值满足如下关系：

1≤ A 1 ≤ A 2 ≤ … ≤ A n ≤n 。不同的问题可以具有相同的分值。

主办方希望：解决更多问题的参赛者的排名更高。 因此，对于任何解决了 k（1 ≤ k ≤ n-1）个问题

的参赛者，其分数总和一定要小于解决了任何 k + 1 个问题的参赛者的分数总和。

你有几种分配分 值 的方法？ 将答案对素数 m 取余后输出。

输入：

整数 n 和 m

其中 2 ≤ n ≤ 5000,9×10 8 <m<10 9 ，m 为素数。

输出：

分值分配的方案数对 m 取余后的数字

样例输入 1：

2 998244353

样例输出 1：

3

样例 1 说明：

2 个题的分值分配有 3 种方案： (1,1), (1,2), (2,2)。

样例输入 2：

3 998244353

样例输出 2：

7

样例 2 说明：

3 个题的分值分配有 7 种方案：(1,1,1), (1,2,2), (1,3,3), (2,2,2), (2,2,3), (2,3,3),

(3,3,3) 。

评分标准：

30 分 ：完成题目样例和给出的一个样例；

50 分 ：在 30 分的基础上完成给出的另外一个样例；

100 分：在 50 分的基础上完成给出的最后一个样例。

1、双面打印

为了环保，妈妈一般都进行双面打印，也就是一张纸的正反面都打印出相应的内容。举个例子来说：如果一份电子材料有3页，那么需要2张纸进行打印；如果一份电子材料有4页，那么还是需要2张纸进行打印。现在已经知道了一份电子版的学习材料的页数N，你能帮小蓝计算一下需要几张纸吗？

输入样例：

7

输出样例：

4

#include<iostream>

using namespace std;

int main() {

int n

cin>>n;

cout<<(n+1)/2;

return 0; }

2、求完数

因子：因子也叫因数，例如3×5=15，那么3和5是15的因子。同时15×1=15，那么1和15也是15的因子。 1，3，5，15 这四个因子是15的所有因子。

完数：如果一个数等于不含它本身的其他因子之和，则称该数为‘完数’。如6的因子有1，2，3，6，且1+2+3= 6，因此6是完数。

题目描述: 输入一个正整数N（0<N<10000）,输出小于N的所有完数及小于N的完数个数（个数前加“*”，例如：*2）。

#include<iostream>
 
using namespace std;
 
int main()
 
{
 
int i,j,n,sum=0,count=0;
 
cin>>n;
 
for(i=1;i<n;i++)
 
{
 
for(j=1;j<i;j++)
 
{
 
 if(i%j==0) sum=sum+j;
 
}
 
if(sum==i)
 
{cout<<i<<endl;
 
count++;
 
}
 
sum=0;
 
}
 
cout<<"*"<<count;
 
return 0;}

3、求阴影部分面积

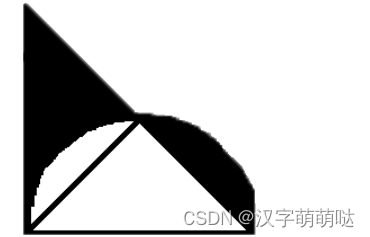
用户输入一个正整数a（0<a<100）,作为如图半圆的直径，同时作为如图等腰直角三角形的直角边长度，求下图的阴影部分面积，并保留两位小数

很简单，只要把半圆阴影移到三角那块就可以了，这样面积就是a*a/2了

只不过要保留两位小数，用double

#include <iostream>
#include <cstdio>
using namespace std;
int main() {
	double a;
	cin>>a;
 printf("%.2f",a*a/4);
	return 0; }

4、判断分数

选择题有5道，都是单选题，每道30分，共计150分。每道选择题选对得30分，选错或不选得0分。假设正确的答案为“DCBAD”，你能根据选手的提交情况，判定选手的选择题总分吗？

选手提交一个由5个字符组成的字符串，代表选手的选项。字符串仅能包含如下5种字符：“D”、“C”、“B”、“A”、“E”。其中“A”、“B”、“C”、“D”代表选手选择了某个选项，而“E”代表选手未做该题。求总分。

先定义一个字符串存放答案，输入选手的选项，通过一个循环和答案比对，只有答对的才加分，最后直接输出

#include <iostream>
using namespace std;
int main() {
	string answer="DCBAD",n;
	int sum=0;
	cin>>n;
	for(int i=0; i<5; i++)
		if (n==answer[i])
			sum=sum+30;
	cout<<sum;
	return 0; }

5、节气

“二十四节气”被列入联合国教科文组织人类非物质文化遗产名录。在国际气象界，这一已有千年历史的时间认知体系被誉为“中国第五大发明”。

春雨惊春清谷天，夏满芒夏暑相连。秋处露秋寒霜降，冬雪雪冬小大寒。二十四节气，在四季轮回流淌，每个节气都有它较为稳定的日子。下表给出了农历庚子年（公历2020年1月25日~2021年2月11日）中，二十四个节气的名称，公历具体日期及汉语拼音的缩写。

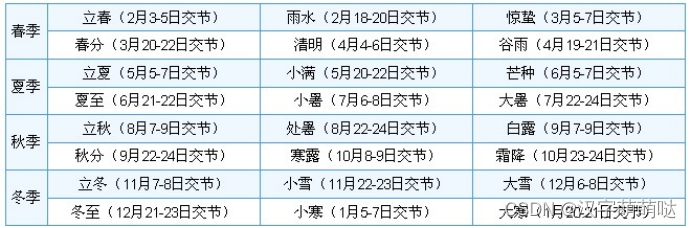
输入描述

整数M，N（2≤M≤12,1≤N≤31），M，N分别代表公历2020年的某月，某日。所给出的数据均为合法日期。

输出描述

如果当天恰好是一个节气，输出这个节气的汉语拼音缩写，如当天不是节气则输出下一个节气的汉语拼音缩写

先把月日和节气的节气缩写放在数组之中，先判断是否正好是节气，再进行判断最近的节气操作。

先判断是否是12月的边界特例，再判断其他情况

其他情况有两种：

1.日期超过了当前遍历的节气，直接continue

2.日期没有超过，直接输出

#include<bits/stdc++.h>
using namespace std;
int x,y,month[25]={1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11,12,12},day[25]={5,20,4,19,5,20,4,19,5,20,5,21,6,22,7,22,7,22,8,23,7,22,7,21};
string jq[25]={"XH","DH","LC","YS","JZ","CF","QM","GY","LX","XM","MZ","XZ","XS","DS","LQ","CS","BL","QF","HL","SJ","LD","XX","DX","DZ"};
int main()
{
    cin>>x>>y;
    for (int i=0;i<24;i++)
        if (month[i]==x&&day[i]==y)
        {
            cout<<jq[i];
            return 0;
        }
 for (int i=0;i<24;i++)//12月末特例
    {
        if (x==12&&y>day[23])
        {
            cout<<jq[0];
            return 0;
        }
        else if (x>month[i]||y>day[i]) continue;//未到时间
        else if (x<=month[i]&&y<day[i])//寻找
        {
            cout<<jq[i];
            return 0;
        }   
    }
}

6、成绩统计

小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是一个 0 到 100 的整数。

如果得分至少是 60 分，则称为及格。如果得分至少为 85 分，则称为优秀。

请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整数。

【输入格式】

输入的第一行包含一个整数 n，表示考试人数。

接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

【输出格式】

输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分四舍五入保留整数。

【样例输入】

7

80

92

56

74

88

100

0

【样例输出】

71%

43%

【评测用例规模与约定】

对于50% 的评测用例， 1 ≤ n ≤ 100。

对于所有评测用例，1 ≤ n ≤10000。

#include<iostream>
using namespace std;
int main() {
	double a1=0,a2=0;
	int n,i,score;
	cin>>n;
	for(i=1; i<=n; i++) {
		cin>>score;
		if(score>=60) a1++;
		if(score>=85) a2++;
	}
	a1=(a1/n+0.005)*100;
	a2=(a2/n+0.005)*100;
	cout<<int(a1)<<"%"<<endl;
	cout<<int(a2)<<"%";
	return 0; }

7、水下探测器

水下探测器可以潜入湖中在任意水深进行科学探索。

湖水的最大深度为 h 米,即它在湖底时到水面的距离，0<=h<=100；

探测器最初的水下深度为 s 米，0<=s<=100；

当探测器不在水面（当前深度大于 0）时，每个 u 指令可使它上浮 1 米，而当探测器在水面时，u 指令是无效的；

当探测器不在湖底（当前深度小于 h）时，每个 d 指令可使它下沉 1 米，而当探测器在湖底时，d 指令是无效的；

在执行到无效指令时，探测器不做任何操作而继续执行下一指令。

编程实现：

根据给定的 h、s 和一个指令序列（由字符 u、d 组成的字符串，长度不超过 100），求出执行完整的指令序

蓝桥杯全国软件大赛青少年创意编程 C++组

列后，探测器的水下深度。

输入：

第一行：h 和 s，以空格分开。0<=s<=h<=100

第二行：长度不超过 100 的指令字符串，串中仅包含字母 u 或 d

输出：

代表探测器在执行指令后的水下深度的数字。

样例输入：

9 1

uduudd

#include <iostream>
using namespace std;
int main() {
	int h,s;
	string str;
	cin>>h>>s>>str;
	for(int i=0; i<str.size(); i++) {
		if(str[i]=='u') {
			if(s>0) {
				s--;
			}
		}
		if(str[i]=='d') {
			if(s<h) {
				s++;
			}
		}
	}
	cout<<s; }

1. 小猫吃鱼

明明家从 1 号站点出发，开车去旅游，一共要经过 n 个站点，依次为 2、3……n。

由于明明带上了心爱的小猫，在每个站点都要为小猫提供一条鱼用做美餐（包括 1 号站点）。

除了 1 号站点只能吃 1 号站点买的鱼，其他站点既可以吃当地买的鱼，也可吃之前经过的站点买了存入车载冰箱中的鱼。但车载冰箱消耗的电能来自汽油，所以每条鱼用冰箱保存到下一站的费用与各个站点的汽油价格有关。

为使问题简化，我们约定：

（1）车从某站开出时油箱中都是此站点刚加的汽油。

（2）车载冰箱能容纳一路上需要的所有鱼。 即：每条鱼的费用既包括购买时的费用，也包括用冰箱保存鱼的费用。

编程实现：

为了降低小猫吃鱼的总代价，明明预先上网查到了这 n 个站点的鱼价和汽油价格。并据此算出每个站点买一条鱼的费用以及从该站点到下一站用冰箱保存一条鱼的费用。你能帮明明算出这一路上小猫吃鱼的最小总费用吗？

输入：

第一行：站点数 n，1<n<100。

接下来的 n 行：每行两个以空格分隔的正整数，表示：这一站买一条鱼的费用，以及从这一站把每条

鱼保存到下一站的费用，两个费用均为小于 10000 的正整数。

输出：

最小总费用，是一个正整数。

样例输入：

5

6 3

7 1

3 2

8 3

9 5

样例输出：

29

使用for循环，每次看看价钱是不是最划算，不是就加上一条鱼，是也要加上这一条鱼，每次还要加上保存的价钱。

#include <iostream>
using namespace std;
int main() {
	int n;
	cin>>n;
	int m1[n], m2[n];
	for(int i = 0; i < n; i++)
		cin>>m1[i]>>m2[i];
	//输入当前买鱼的钱和保存的钱
	int min = 9999999, t = 0;
	for(int i = 0; i < n; i++) {
		if(min > m1[i])
			min = m1[i];
		t = t + min; //上一条鱼
		min = min + m2[i]; //保存
	}
	cout<<t<<endl;
	return 0;
}

9、最大购物优惠

小惠听说超市正在打折促销，要制订一个得到最大优惠的购物计划。

小惠的体力可以提起 w 单位重量的东西，还有一个能装 V 个单位体积的购物袋，并详细了解了各打折商品的重量、体积及此商品实际优惠的金额。她想在自己体力的限度和购物袋容积限度内，尽可能多地得到购物优惠。

超市规定这些打折商品每种只能购买一件。

编程实现：

请你编写程序，制定一个购买商品的计划，求出小惠能得到的最大优惠金额和实际应购买的各商品序号。

输入：

第一行：依次为 w、v 和 n(n 为商品种类数)，所有数值均为不超过 100 的正整数

接下来的 n 行：每行有三个整数，依次为某种商品的重量、体积和让利金额，数值间以空格分开，所有数值均为不超过 100 的正整数

输出：

第一行：小惠能够得到的最大让利金额

第二行：依次为从小到大排列的商品序号，序号从 1 开始，序号间用空格分开。若第二行输出的序列

不唯一，则输出其最小字典序。

样例输入：

10 9 4

8 3 6

5 4 5

3 7 7

4 5 4

样例输出：

9

2 4

10、购物单

XX大促销又来了，长长的购物单，都是有打折优惠的。

请你帮他计算一下，需要从取款机上取多少现金，才能搞定这次购物。

取款机只能提供100元面额的纸币。小明想尽可能少取些现金，够用就行了。

你的任务是计算出，小明最少需要取多少现金。

180.90       88折

10.25       65折

56.14        9折

104.65        9折

100.30       88折

297.15       半价

26.75       65折

130.62       半价

#include <iostream>
#include <fstream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
int main()
{
    ifstream in("test01.txt");
    double value, discount;
    int ans = 0;
    double tmp = 0;
    while (in >> value >> discount)
    {
        tmp += value * discount;
        if (ans < tmp)
        {
            while (ans < tmp) {
                ans += 100;
            }
        }
    }
    cout << ans << endl;    
        
return 0;}

11、等差素数列

2,3,5,7,11,13,....是素数序列。

类似：7,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。

上边的数列公差为30，长度为6。

2004年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。

这是数论领域一项惊人的成果！有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为10的等差素数列，其公差最小值是多少？

注意：需要提交的是一个整数，不要填写任何多余的内容和说明文字。

先用埃氏筛法，把1~N (N先设置一个10000吧，不够再加)以内的素数都筛选出来，然后再枚举 1~10000(公差，不够再加)，寻找连续10个的素数。

#include <iostream>
using namespace std;
const int maxn = 10000000;
int prime[maxn];
bool is_prime[maxn + 10];  //is_prime[i]为true表示i是素数 
bool is_Prime(int n)
{
    int i = 0;
    for (i = 2; i * i <= n; i++)
    {
        if (n % i == 0) return false;
    }
    return n != 1; 
}
//返回n以内的素数
int sieve(int n)
{
    int p = 0;
    //初始化
    for (int i = 0; i <= n; i++) {
        is_prime[i] = true;
    }
    is_prime[0] = is_prime[1] = false;
            
    for (int i = 0; i <= n; i++)
    {
        if (is_prime[i]) 
        {
            prime[p++] = i;  //将素数添加到prime中
            //1.首先2是素数, 然后划去所有2的倍数
            //2.表中剩余的最小数字是3, 他不能被更小的数整除,所以是素数
            //再将表中所有3的倍数都划去
            //3.以此类推, 如果表中剩余的最小数字是m时,m就是素数。然后将表中所有m的倍数都划去
            for (int j = 2 * i; j <= n; j += i) {
                is_prime[j] = false;
            } 
        }
    }
    return p;
} 
void solve()
{
    int N = 10000;
    int cnt = sieve(N);
    
    //公差 
    for (int d = 10; d < N; d++)
    {
        //枚举N以内所有素数 
        for (int i = 0; i < cnt; i++)
        {
            int tmp = prime[i],
                flag = true;
            //是否连续10个都为素数 
            for (int j = 0; j < 9; j++)
            {
                if (tmp + d > N || !is_Prime(tmp + d)) 
                {
                    flag = false;
                    break;
                }
                else
                {
                    tmp += d;  //下一个素数    
                }
            }
            if (flag) {
                cout << d << " " << prime[i] << endl;
                return;
            }
        }
    }
    
    
}
int main()
{
    solve();
    return 0;
    
}

1. Fibonacci数列

Fibonacci数列的递推公式为：Fn=Fn-1+Fn-2，其中F1=F2=1。

当n比较大时，Fn也非常大，现在我们想知道，Fn除以10007的余数是多少。

输入格式 输入包含一个整数n。 输出格式 输出一行，包含一个整数，表示Fn除以10007的余数。

说明：在本题中，答案是要求Fn除以10007的余数，因此我们只要能算出这个余数即可，而不需要先计算出Fn的准确值，再将计算的结果除以10007取余数，直接计算余数往往比先算出原数再取余简单。

样例输入 10 样例输出 55 样例输入 22 样例输出 7704 数据规模与约定 1 <= n <= 1,000,000

#include <stdio.h>
int main()
{
    unsigned long s=0,f1=1,f2=1,f3=1,n=0;
    scanf("%d",&n);
     if(n>2)
    for(s=3;s<=n;s++)
    {
         f3=(f2+f1)%10007;
         f1=f2;
         f2=f3;
     }
     printf("%d",f3);
     return 0;
 }

程序填空：

标题：取数位

求1个整数的第k位数字有很多种方法。

以下的方法就是一种。

// 求x用10进制表示时的数位长度

int len(int x){

    if(x<10) return 1;

    return len(x/10)+1;

}

// 取x的第k位数字

int f(int x, int k){

    if(len(x)-k==0) return x%10;

    return _____________________;  //填空       答案：f(x/10,k)

}

int main()

{

    int x = 23574;

    printf("%d\n", f(x,3));

    return 0;

}

13、图片旋转

图片旋转是对图片最简单的处理方式之一，在本题中，你需要对图片顺时针旋转 90 度。

我们用一个 n × m 的二维数组来表示一个图片，例如下面给出一个 3 × 4 的图片的例子：

1 3 5 7

9 8 7 6

3 5 9 7

这个图片顺时针旋转 90 度后的图片如下：

3 9 1

5 8 3

9 7 5

7 6 7

给定初始图片，请计算旋转后的图片。

【输入格式】

输入的第一行包含两个整数 n 和 m，分别表示行数和列数。

接下来 n 行，每行 m 个整数，表示给定的图片。图片中的每个元素（像素）为一个值为 0 至 255 之间的整数（包含 0 和 255）。

【输出格式】

输出 m 行 n 列，表示旋转后的图片。

【样例输入】

3 4

1 3 5 7

9 8 7 6

3 5 9 7

【样例输出】

3 9 1

5 8 3

9 7 5

7 6 7

【评测用例规模与约定】

对于 30% 的评测用例，1 ≤ n, m ≤ 10。

对于 60% 的评测用例，1 ≤ n, m ≤ 30。

对于所有评测用例，1 ≤ n, m ≤ 100。

#include <bits/stdc++.h>
using namespace std;
 
int main()
{
    int n, m;
    cin >> n >> m;
    int map[200][200];
    for (int i = 0; i < n; i++)
        for (int j = 0, t; j < m; j++)
            cin >> map[i][j];
 
    for (int i = 0; i < m; i++)
        for (int j = n - 1; j >= 0; j--)
            cout << map[j][i] << (j==0?'\n':' ');
    return 0;}

14、质数

我们知道第一个质数是 2、第二个质数是 3、第三个质数是 5……请你计算 第 2019 个质数是多少？

#include<iostream>
#include<cmath>
using namespace std;
int zs(int a) {
	for (int i = 2; i <= sqrt(a); i++) {
		if (a % i == 0)
			return 0;
	}
	return 1;
}
int main() {
	int cnt = 0,i=1;
	while(cnt<2019) 
{	i++;
	if (zs(i) == 1)
		cnt++;
	}
	cout << i ;
	return 0;
}

15、年号字串

小明用字母 A 对应数字 1，B 对应 2，以此类推，用 Z 对应 26。对于 27 以上的数字，小明用两位或更长位的字符串来对应，例如 AA 对应 27，AB 对 应 28，AZ 对应 52，LQ 对应 329。

请问 2019 对应的字符串是什么？

#include <bits/stdc++.h>
using namespace std;
 
int main()
{
    int m = 2019;
    while( m!=0)
    {
        int t = m%26;
        m=m/26;
        cout << char(t+64);
    }
    //system("pause");
    return 0;
}
/*
输出：QYB
答案：BYQ*/

16、矩形切割

小明有一些矩形的材料，他要从这些矩形材料中切割出一些正方形。

当他面对一块矩形材料时，他总是从中间切割一刀，切出一块最大的正方 形，剩下一块矩形，然后再切割剩下的矩形材料，直到全部切为正方形为止。

例如，对于一块两边分别为 5 和 3 的材料（记为 5×3），小明会依次切出 3×3、2×2、1×1、1×1 共 4 个正方形。

现在小明有一块矩形的材料，两边长分别是 2019 和 324。请问小明最终会 切出多少个正方形？

#include <bits/stdc++.h>
using namespace std;
int work(int a, int b)
{
    if (a == b)
        return 1;
    int k = min(a, b);
    int l = max(a, b);
    return work(k, l - k) + 1;
}
int main()
{
    int a = 2019, b = 324;
    cout << work(a, b) << endl;
    //system("pause");
    return 0;
}