社交网络图中结点的“重要性”计算 (30 分)(Floyd)_设计题目4:社交网络图中节点的“重要性”计算 1.设计目的: (1) 熟练掌握图的存储

在社交网络中，个人或单位（结点）之间通过某些关系（边）联系起来。他们受到这些关系的影响，这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用，可以增强也可以减弱。而结点根据其所处的位置不同，其在网络中体现的重要性也不尽相同。

“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标，即一个有较高中心性的结点比有较低中心性的结点能够更快地（平均意义下）到达网络中的其它结点，因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中，结点v​i​​ 的“紧密度中心性”Cc(v​i​​ )数学上定义为v​i​​ 到其余所有结点v​j​​ (j≠i) 的最短距离d(v​i​​ ,v​j​​ )的平均值的倒数：

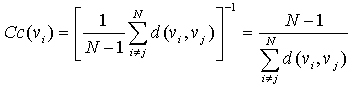
对于非连通图，所有结点的紧密度中心性都是0。

给定一个无权的无向图以及其中的一组结点，计算这组结点中每个结点的紧密度中心性。

输入格式:
输入第一行给出两个正整数N和M，其中N（≤10​4​​ ）是图中结点个数，顺便假设结点从1到N编号；M（≤10​5​​ ）是边的条数。随后的M行中，每行给出一条边的信息，即该边连接的两个结点编号，中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K（≤100）以及K个结点编号，用空格分隔。

输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性，每个输出占一行，结果保留到小数点后2位。

题目思路：
1.采用Floyf算法可以把每个顶点到其他所有点的最短路径算出来这是关键的一点。
2.注意在对图进行初始化的时候，用fill( Graph[0],Graph[0]+ MAXNMAXN, INF )会导致内存超限，因此采用二重循环，只对nn大小进行初始化。
3.最后需要注意，采用Floyd算法以后，如何判断一个是否为 非连通图。通过一个for循环，查看任意一行中有没有INF值。（如果连通，Floyd以后，每个点必定能到达其他所有点）

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 10005;
const int INF = 0x3f3f3f3f;
int Graph[MAXN][MAXN];
void Floyd();
int n, m, k;
int main()
{

	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
		{
			if (i == j)
				Graph[i][j] = 0;
			else
				Graph[i][j] = INF;
		}

	int a, b, t;
	while (m--)
	{
		cin >> a >> b;
		Graph[a][b] = Graph[b][a] = 1;
	}

	Floyd();
	int flag = 1;
	for (int i = 1; i <= n; i++)
		if (Graph[1][i] == INF)
		{
			flag = 0;
			break;
		}
	cin >> k;
	while (k--)
	{
		cin >> t;
		double sum = 0;
		for (int i = 1; i <= n; i++)
		{
			if (Graph[t][i] != INF)
				sum += Graph[t][i];
		}
		double average = (1.0 * (n - 1)) / sum;
		printf("Cc(%d)=%.2f\n", t, flag ? average : 0);
	}

	return 0;
}
void Floyd()
{
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				if (Graph[i][k] + Graph[k][j] < Graph[i][j])
					Graph[i][j] = Graph[i][k] + Graph[k][j];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61