LATR：3D Lane Detection from Monocular Images with Transformer_latr: 3d lane detection from monocular images with

参考代码：LATR

动机与主要工作：
之前的3D车道线检测算法使用诸如IPM投影、3D anchor加NMS后处理等操作处理车道线检测，但这些操作或多或少会存在一些负面效应。IPM投影对深度估计和相机内外参数精度有要求，anchor的方式需要一些如NMS的后处理辅助。这篇文章主要的贡献有两点：

• 1）针对车道线的特性基于DETR目标检测算法提出了一种基于landline query的检测方法，为了使得query的初始化更合理借鉴了SparseInst方法从2D图像域中用不同实例来初始化query，并且建立车道线query的粒度不是车道线级别而是具体到了车道线上的点。
• 2）用图像特征作为key和val是较难去学习其中的3D信息的，在相机内外参数已知情况下构建一个可学习的3D空间位置编码，通过decoder中多轮迭代和与图像特征融合预测残差方式，不断修正3D空间位置编码。

检测器的结构：
这篇文章的方法流程见下图所示：

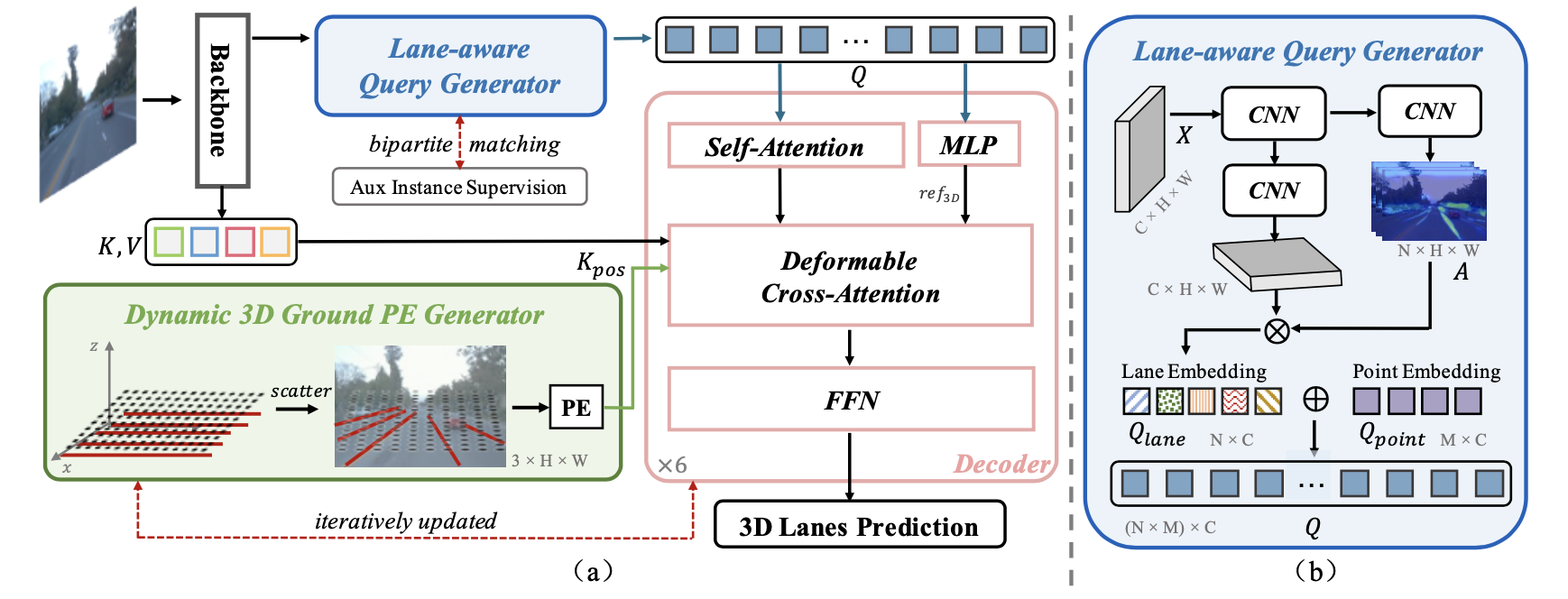
可以从上图中看到backbone出来之后接一个车道线实例预测网络，由此实现lane query生成和初始化。对于图像特征使用3D信息嵌入的位置编码，只不过这个位置编码是在给定一个的初始化基础上修正而来的，也就是说在transformer解码的过程中这个位置编码的值是动态的。

车道线query构建：
这部分参考SparseInst中对于inst feature的构建过程，具体可以去查阅对应的论文，由此可以得到车道线query的特征表达$Q_{lane}\in R^{N\ast C}$（这里是从特征图尺寸最大的那个特征上得到的）。而对于车道线来说，其是由多个点组成的，那么还需要对上面的点构建query，这里通过设定可学习的参数来实现$Q_{}\in R^{M\ast C}$。那么接下来就是使用broadcast机制实现最后车道线的query构建$Q\in R^{(N\ast M)\ast C}$

实例+点query的形式效果才是最好的：

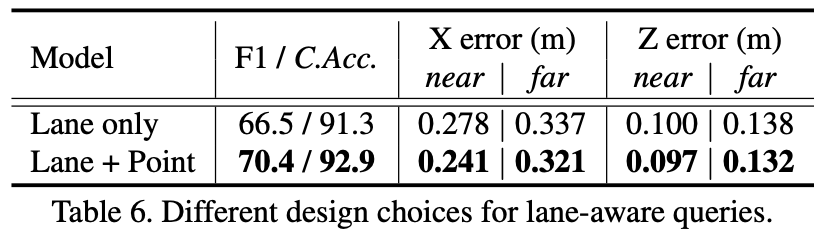
图像feature的位置编码：
这里关注的是自动驾驶场景下的车道线，则根据车道线的分布特点可以为对应2D图像特征设置位置编码。这里的位置编码是首先在3D空间中进行采样（也就是文章定义的3D地平面），之后通过相机内外参数投影到图像中，以此来作为对应图像位置处的3D位置来源。只不过这里的3D地平面是动态更新的，在transformer的不同层中会预测不同的更新残差，定义的残差变量有旋转角度（偏航角）$\Delta \theta$和平面高度$\Delta h$，其预测是通过一组FC层实现的：
$$[\Delta \theta ,\Delta h]=MLP(AvgPool(\mathcal{G}[X,M_p]))$$
其中，$\mathcal{G},X,M_p$分别代表2层卷机操作、图像特征、上一轮的地平面的位置编码。

则新一轮的平面点会使用下面的矩阵进行更新：

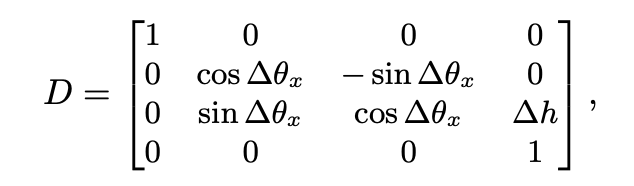
则在原本不准确的3D平面上就可以通过自适应回归的方式优化3D地平面，由此实现特征3D位置编码的优化。此外，地平面的约束还使用过车道线上的点投影建立起来
$$L_{plane}=\sum _{u,v\in \mathcal{P}\cap \mathcal{L}}||M_p[:,u,v]-M_l[:,u,v]|{|}_2$$

最终的效果也就是使得下图中的绿色平面与红色的车道线接近。不过截止10.09.2023这部分的代码并没有开放出来。下图展示了地平面会随着迭代的进行收敛到实际车道线的位置上：

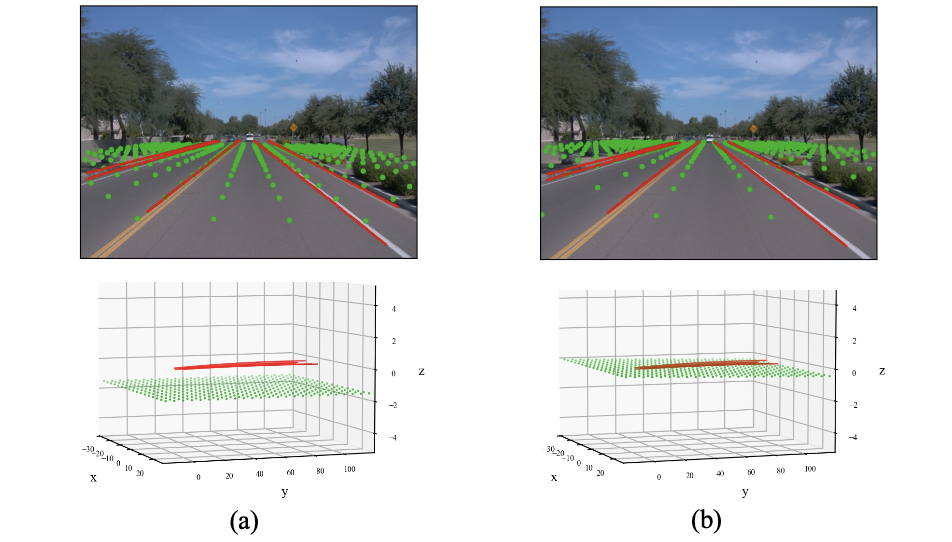
分析位置编码的作用，首先看位置编码带来的性能提升：

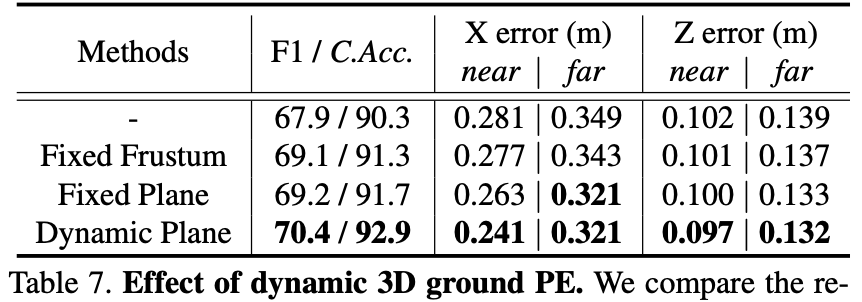
从上表可以看到位置编码确实能带来性能的提升，无论是视锥还是固定平面编码，只不过这里动态平面编码的方式更加适合车道线，因而相比起来有1个点的提升。这里说明准确的位置编码有助于得到更好的检测性能，而且文章提出的平面优化自由度只有2个，更多的维度是否能更好呢？

车道线query+位置编码两者对检测性能的影响：

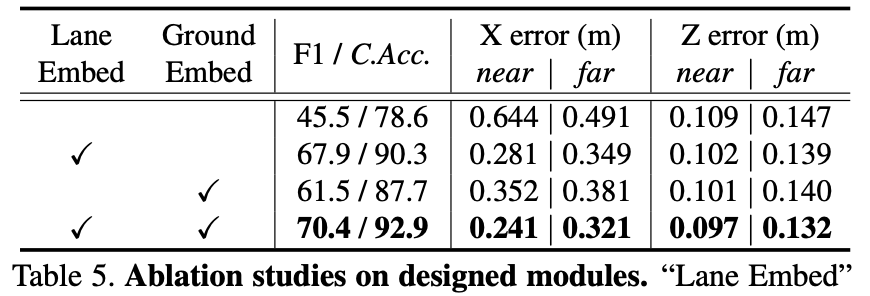
对于后面车道线的解码部分就跟传统的DETR一致了，这里就不做展开。

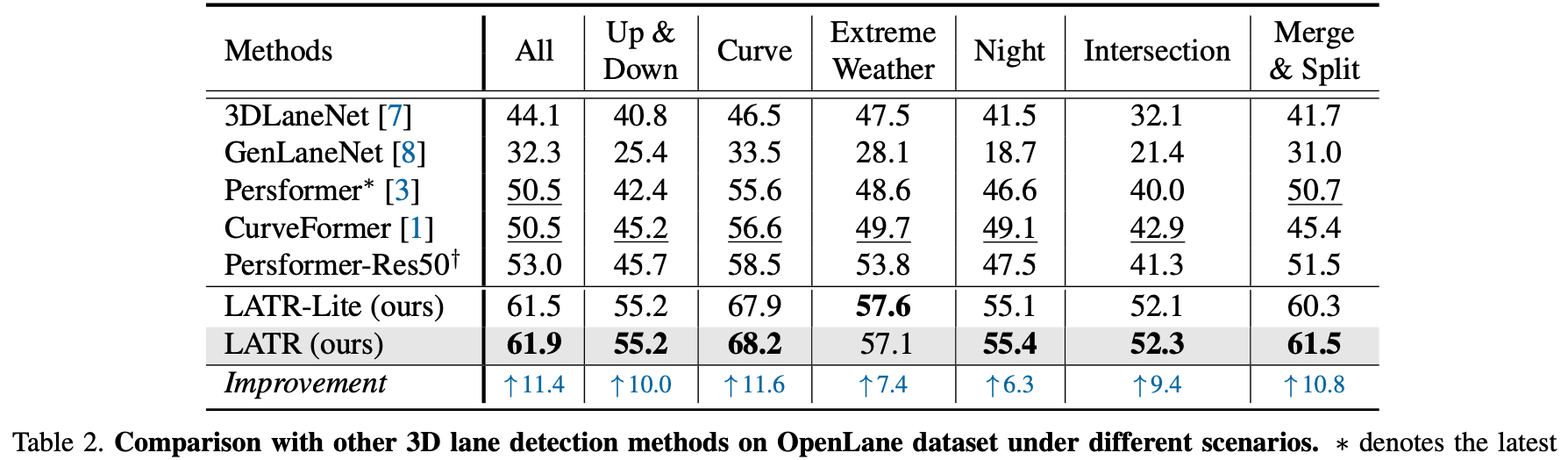
不同数据集下的性能表现：
OpenLane validation：

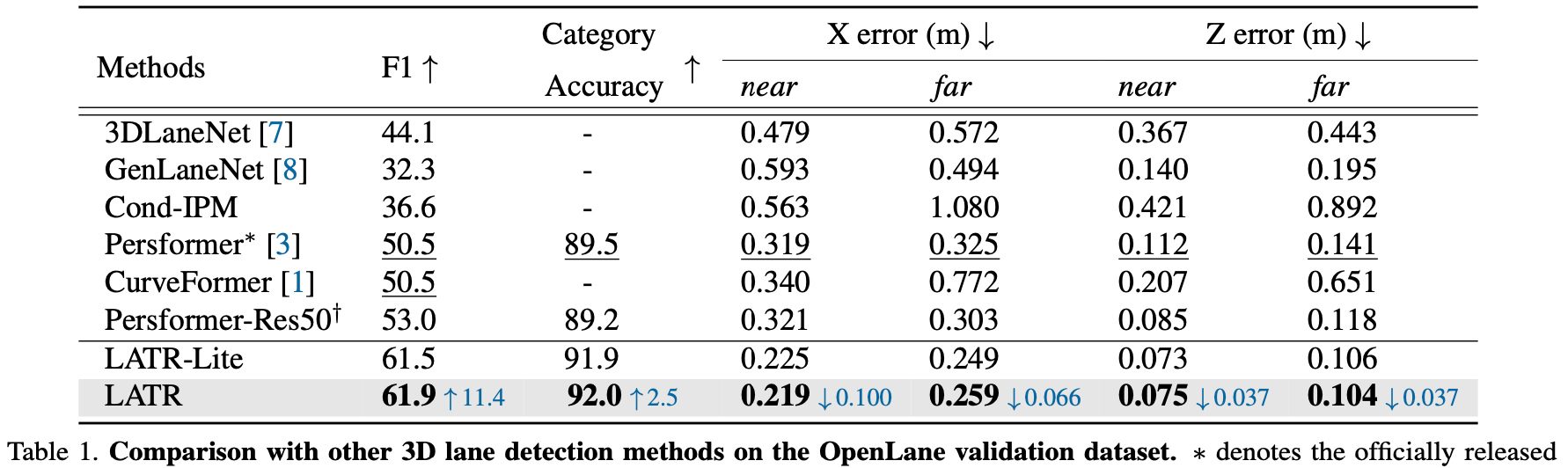
OpenLane不同天气条件下的表现