- 12023值得推荐的高颜值Vue3.0 Web PC端UI框架,赶紧收藏学习!_vue3 ui框架
- 2自定义Inspector绘制默认Scrip栏怎么绘制_inspector绘制方式
- 3AttributeError: module 'cv2.cv2' has no attribute 'face' 模块'cv2.cv2'没有属性'face'_attributeerror: module 'cv2' has no attribute 'fac
- 4Docker学习笔记03:linux操作系统内核升级_4.1.12-124.16.4.el6uek.x86_64
- 5JS特效第134弹:jQuery响应式全屏背景图片导航菜单特效
- 6linux查看资源使用率,Linux中查看系统资源占用情况的命令――二
- 7yarn : 无法将“yarn”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确 保路径正确,然后再试一次。 所在位置 行:1 字符: 1 + ya
- 8【Springboot + Vue 视频播放web项目】解决视频播放只有声音没有画面_vue 播放器能收到数据,但没有画面
- 9Android:自定义控件
- 10【教程】使用docker搭建WebDAV服务_docker webdav
数学向量基本知识_向量基础知识
赞
踩
数学向量基本知识
1.向量相关定义
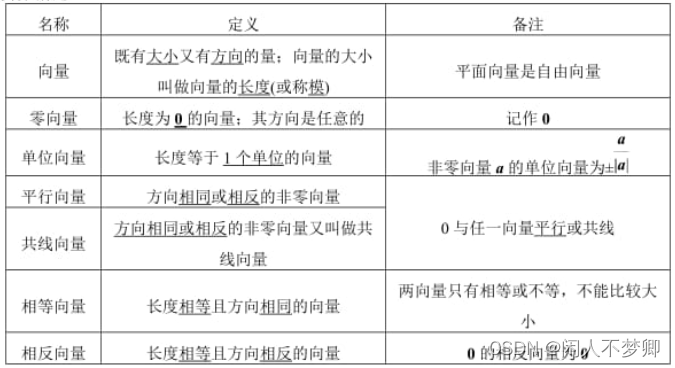
2.向量的线性运算
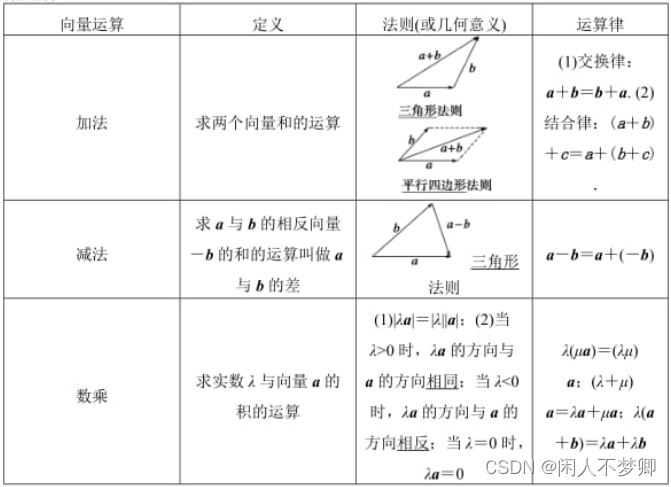

3.向量积与数量积
向量积与数量积的区别
| 名称 | 标积/内积/数量积/点积 | 矢积/外积/向量积/叉积 |
|---|---|---|
| 运算式(a,b和c粗体字,表示向量) | a·b=|a||b|·cosθ | a×b=c,其中|c|=|a||b|·sinθ,c的方向遵守右手定则 |
| 几何意义 | 向量a在向量b方向上的投影与向量b的模的乘积 | c是垂直a、b所在平面,且以 |
| 运算结果的区别 | 标量(常用于物理)/数量(常用于数学) | 矢量(常用于物理)/向量(常用于数学) |
3.1 向量积
向量积可以被定义为:
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
方向: a向量与b向量的向量积c的方向与这两个向量所在平面垂直,遵守右手定则(右手法则:用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向。 )
公式: 设a=(x1,y1,z1),b=(x12,y2,z2),i,j,k分别是X,Y,Z轴方向的单位向量,则axb等于如下(借助三阶行列式运算,就是这样定义的)。从结果我们看出还保留向量的基本单位i、j、k,所以结果也是一个向量,既有大小,又有方向:axb=(y1z2-z1y2,z1x2-x1z2,x1y2-y1x2)

二维向量叉乘公式a(x1,y1),b(x2,y2),则a×b=(x1y2-x2y1),不需要证明的就是定义的运算。
三维叉乘是行列式运算,也是叉积的定义,你把第三维看做0代入就行了。

几何意义:

以向量a和向量b构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的面积相等。


3.1 数量积
向量点乘(内积):
点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product),结果就是个数,把方向给抹去了。向量是有两个属性的:大小和方向,点乘的结果就是得到一个标量。相等于降维了。

定义为:对两个向量对应位置上的值相乘再相加的操作,其结果即为点积。

从这个结果来看,就知道没有方向属性,只是数字之间的运行,最终结果也是数字。
从几何角度看,点积是两个向量的长度与它们夹角余弦的积。点乘的结果表示向量A在向量B方向上的投影与向量B模的的乘积
点乘的意义:
- 两个向量在一个向量方向的共同积累的结果,但是这种结果只保留的大小属性,抹去了方向这个属性;
- 同时反映了两个向量在方向上的相似度,结果越大越相似;
- 基于结果可以判断这两个向量是否是同一方向,是否正交垂直,具体对应关系为:
大于0.则方向基本相同,夹角在0°到90°之间
0则正交,相互垂直
小于0则方向基本相反,夹角在90°到180°之间
垂直和正交的区别:

法向量与平面
法向量:垂直于平面的向量称为该平面的法向量(normal vector)
假设平面上的一个定点为,平面上的任何其它点为,平面的法向量为:

向量 位于平面上,且与法向量 垂直,因此:




R3中平面的一般形式即:

总结:法向量和平面上的一个定点,可以定义该平面


