One PUNCH Man——交替最小二乘推荐算法_one punch vk

交替最小二乘推荐算法

ALS(Alternating Least Square)，交替最小二乘法。在机器学习中，特指使用最小二乘法的一种协同推荐算法。
如下图所示，u表示用户，v表示商品，用户给商品打分，但是并不是每一个用户都会给每一种商品打分。比如用户u6就没有给商品v3打分，需要我们推断出来，这就是机器学习的任务。

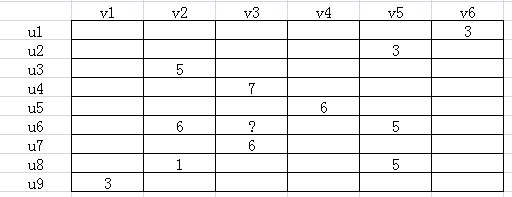
注意：虽然这个表在上图看起来很小，实际上这个表是很大的，行列一般以万/十万/百万/千万计数。

由于并不是每个用户给每种商品都打了分，可以假设ALS矩阵是低秩的，即一个mn的矩阵，是由mk和k*n两个矩阵相乘得到的，其中k<<m,n。

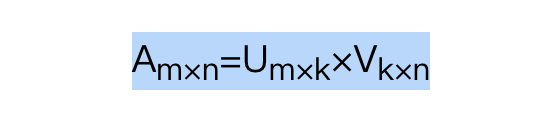
这种假设是合理的，因为用户和商品都包含了一些低维度的隐藏特征，比如我们只要知道某个人喜欢碳酸饮料，就可以推断出他喜欢百世可乐、可口可乐、芬达，而不需要明确指出他喜欢这三种饮料。这里的碳酸饮料就相当于一个隐藏特征。上面的公式中，Um×k表示用户对隐藏特征的偏好，Vk×n表示产品包含隐藏特征的程度。这个k就是商品Product的潜在因素，用来解释数据中的交互关系。

注意：由于k的值很小，所以这种分解算法只能是一种近似值，并不是绝对的上述说的等式。

原始的矩阵是低秩的，也就是稀疏的，但UV的乘积是却稠密的，即该矩阵存在较少的非0元素。因此，该约等式只是一种近似，原始矩阵大量元素是缺失的（因为缺失，默认为0，但可能实际上不为0），而算法为原始矩阵补全了大部分缺失值。从这个角度来看，矩阵分解的算法有时候称为矩阵补全算法。

第三次强调了，UV的乘积只是尽可能的逼近A，用数学的话来讲就是无限趋近于A。怎么求解呢？ALS算法呼之欲出！
首先我们简写前面的公式为下：
$A=X^{T}Y$

不幸的是，上述的$A=X^{T}Y$ 通常没有解，因为$X^{T}Y$ 通常不够大！也就是说，我们找到的分解矩阵X和Y的阶太小了，无法完美的表示A。其实这不完全是坏事，因为A归根到底只是现实中的一个微小样本，它只是一次观察，而且是很稀疏的观察。就比如拼图里，很多拼板都掉了，虽然拼图最后的图样是一只猫，但是手上的拼板太少的时候，就很难看到正确的图案。

所以，另一个由上述公式推导化为：
$A_{i}Y(Y^{T}Y{)}^{-1}=X_i$
这个公式如何理解呢？
首先A是已知的，要求解矩阵$X$和矩阵$Y$。那么根据上述公式，只需要知道一个另一个通过公式推导也是能够知道的。
比如知道矩阵$Y$，那么，因为$X$的第$i$行是根据$A$的第$i$行和$Y$的函数得到的，所以只需要根据上述公式，一行一行求出$X$即可。
要想两边精确相等是不可能的，因此，实际的目的是最小化的$|A_{i}Y(Y^{T}Y{)}^{-1}-X_i|$ ，或者是最小的矩阵平方误差，这也是“最小二乘”的由来。

实际上，在编码中，虽然公式中说明了行向量的计算方法，但是实践中从来不会对矩阵求逆。我们一般会借助QR分解之类的方法，更快更直接的计算。
QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。用一张图可以形象地表示QR分解：

这其中， 为正交矩阵，，R为上三角矩阵。

详见 https://www.cnblogs.com/AndyJee/p/3846455.html

回归正题：
只要知道一个$Y$，那么我们就能逐行求出$X$。求出的这个$X$又可以通过这个公式求出新的$Y$，新的$Y$又可以求出新的$X$…子子孙孙无穷匮也。这时候，智叟说了一句，愚公你有老婆么？愚公老婆都没有，怎么会有子孙呢？
那么愚公的老婆哪里来呢？即这个$Y$怎么来呢？有小朋友说，我们可以给它new个对象。
嗯，没错，这个$Y$就是人为“瞎编”出来的，并且是随机的。而$X$是最优化计算出来的，这个$Y$是假的无所谓，我们又可以用计算出来的$X$计算出新的$Y$。这个过程一直继续，$X$和$Y$都会收敛到一个合适的结果，也就是“交替”一词的来历。

ALS算法页可以利用输入数据是稀疏的这一点，可以用简单的线性代数运算最优解，以及数据本身可并行化，这三点解释了Mlib为什么要使用ALS算法， 并且也只有ALS算法作为唯一的一种推荐算法。