生存分析序章2——生存分析之Python篇：lifelines库入门_python的lifelines

写在开头

数据分析和挖掘在当今信息时代扮演着至关重要的角色。生存分析作为其中一项重要的统计学方法，被广泛应用于医学、工程、金融等领域，帮助我们理解事件发生与时间的关系。在本文中，我们将深入介绍Python中的lifelines库，探讨其在生存分析中的应用。

1. 介绍 lifelines 库

1.1 lifelines库简介

lifelines是一个专注于生存分析和可靠性分析的Python库。它提供了丰富的功能，包括生成生存曲线、构建比例风险模型等。lifelines的设计旨在使分析人员能够更轻松地理解和模型化事件的发生与时间的关系。

1.2 安装与环境配置

在使用lifelines之前，首先需要安装该库并进行环境配置。可以通过以下步骤完成：

步骤一：安装lifelines库

在命令行或终端中运行以下命令：

pip install lifelines
1

步骤二：导入lifelines库

在Python脚本或Jupyter Notebook中，导入lifelines库：

import lifelines
1

步骤三：检查安装是否成功

在Python环境中运行以下代码，确保成功安装了lifelines库：

print(lifelines.utils.__version__)
1

以上步骤简明扼要，确保你在开始生存分析之旅前，已经顺利配置了lifelines库。

2. 数据准备

2.1 数据格式与结构

在进行生存分析之前，首先需要理解lifelines库对数据的要求。一般而言，lifelines接受一个包含生存时间、事件发生情况以及其他相关变量的数据集。让我们更深入地了解一下这些数据。

生存时间（Duration）和事件发生情况（Event）： 这两个是最基本的变量。"生存时间"表示从某一起始点到事件发生或观察结束的时间长度，而"事件发生情况"表示在观察期内是否发生了事件。下面是一个简化的示例：

| ID | 生存时间 | 事件发生（1）/未发生（0） | 其他变量1 | 其他变量2 |
|----|----------|-------------------------|----------|----------|
| 1  | 12       | 1                       | 25       | Male     |
| 2  | 24       | 0                       | 30       | Female   |
| 3  | 8        | 1                       | 22       | Male     |
| 4  | 36       | 1                       | 28       | Female   |
1
2
3
4
5
6

在这个示例中，"生存时间"表示观察到事件或观察结束的时间点，"事件发生情况"表示该时间点是否发生了事件。其他变量则可用于进一步细化模型。

在Python中，我们可以使用pandas库加载和处理这样的数据。下面是一个简单的示例代码：

import pandas as pd

# 构建测试数据集
data = pd.DataFrame({
    'time': [5, 10, 12, 18, 25, 30, 35, 40, 45, 50],
    'event': [1, 1, 0, 1, 1, 0, 1, 0, 1, 1],
    'sex':[1, 0, 1, 1, 0, 1, 1, 0, 0, 1],
})

df = pd.DataFrame(data)

# 打印数据框的前几行
print(df.head())
1
2
3
4
5
6
7
8
9
10
11
12
13

运行上述代码后，截图如下：

2.2 处理缺失数据

lifelines库对于缺失数据有一定的鲁棒性，但在进行生存分析之前，最好对缺失值进行处理以确保模型的准确性。常见的处理方法包括删除包含缺失值的行或使用插值方法进行填充。

删除包含缺失值的行： 可以通过dropna()方法删除包含缺失值的行。

使用中位数进行缺失值填充： 对于数值型变量，可以使用中位数进行填充，以保持数据的整体分布。

以下是一个处理缺失值的示例代码：

# 删除包含缺失值的行
df_cleaned = df.dropna()

# 使用中位数进行缺失值填充
df_filled = df.fillna(df.median())

# 打印处理后的数据框
print("删除缺失值后的数据框：")
print(df_cleaned)

print("\n使用中位数填充缺失值后的数据框：")
print(df_filled)
1
2
3
4
5
6
7
8
9
10
11
12

需要注意的是，在处理缺失值时，应该根据数据的实际情况选择合适的方法。此外，如果缺失值的处理会影响到生存时间和事件发生的信息，需要谨慎处理以避免引入偏见。

2.3 对异常值的处理

除了缺失值，异常值也可能对生存分析产生影响。异常值可能导致模型不稳定或不准确，因此在建模之前需要对其进行处理。

识别异常值： 使用统计学方法或可视化工具来检测异常值，例如箱线图、直方图等。

处理异常值： 可以选择删除异常值或使用替代值进行替换。删除可能导致信息损失，因此替代值的选择需谨慎。

以下是一个简单的处理异常值的示例代码：

# 使用箱线图检测异常值
import seaborn as sns
import matplotlib.pyplot as plt

# 绘制生存时间的箱线图
sns.boxplot(x=df['time'])
plt.show()

# 假设定义生存时间大于50为异常值，将其替换为中位数
df['time'] = df['time'].apply(lambda x: df['time'].median() if x > 50 else x)
1
2
3
4
5
6
7
8
9
10

在实际应用中，异常值的处理方式取决于具体情况和数据分布。合理的异常值处理可以提高生存分析模型的鲁棒性和可靠性。

3. Kaplan-Meier 曲线

Kaplan-Meier曲线是生存分析的重要工具之一。我们将学习如何使用lifelines库生成和可视化这一经典的曲线，以揭示时间对事件发生的影响。

3.1 使用 lifelines 绘制生存曲线

Kaplan-Meier估计器是生存分析领域最常用的非参数方法之一。它用于估计在给定时间点上生存函数的概率，即事件发生前的生存概率。lifelines库中的KaplanMeierFitter类实现了这一过程，并提供了简单而强大的工具来可视化和分析生存曲线。

应用场景：

• 医学研究： 用于分析患者的生存时间，例如疾病诊断后的生存概率。
• 产品寿命分析： 估计产品在特定时间内不发生故障的概率。
• 金融领域： 用于估计投资组合或资产的寿命分布。

注意事项：

• 右删失假设： Kaplan-Meier曲线基于右删失假设，即当一个样本发生事件时，其后续观察将被忽略。这是因为我们无法观察到它们何时会发生事件，所以我们在分析中将它们当作在研究期间“幸存”下来的个体。
• 时间间隔离散化： 数据需要以时间点形式提供，因此可能需要对时间进行离散化，例如将时间按月或按年分组。

python代码构建Kaplan-Meier 曲线

下面将通过一段简单的代码，构建简单的Kaplan-Meier 曲线，使用的数据为本篇文章中章节2的数据。

from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt

# 创建KaplanMeierFitter对象
kmf = KaplanMeierFitter()

# 输入生存时间和事件发生情况数据
kmf.fit(durations=df['time'], event_observed=df['event'])

# 绘制生存曲线
kmf.plot_survival_function()
plt.title('Kaplan-Meier Survival Curve')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13

运行上述代码后，我们得到对应的Kaplan-Meier曲线，截图如下：

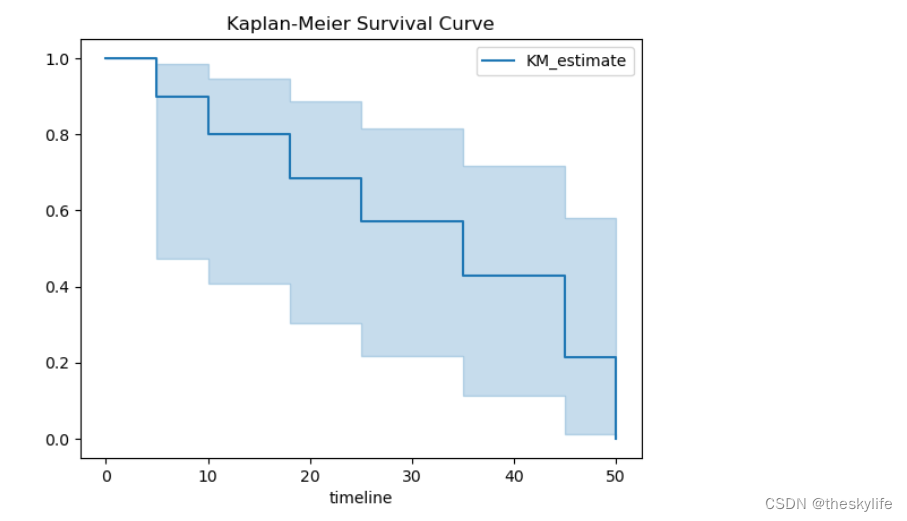
3.2 曲线解读

Kaplan-Meier 曲线是一种常用于生存分析的图形，用于估计时间直到事件发生的生存函数。下面是如何解读 Kaplan-Meier 曲线的一些建议：

• X 轴（时间轴）： X 轴表示时间的流逝，通常以单位时间（如月或年）为刻度。曲线的起点表示研究开始的时刻，而终点表示研究结束的时刻。

• Y 轴（生存概率轴）： Y 轴表示生存概率。生存概率是指在给定时间点生存下来的概率。曲线的起点对应于 100% 的生存概率，而曲线下降的部分表示事件（例如死亡、疾病复发）发生的情况。

• 曲线的步进： Kaplan-Meier 曲线以阶梯状的方式向下移动，每一步代表一个事件的发生。曲线每下降一个步进，都表示有个体经历了事件，因此生存概率下降。

• 曲线间的比较： 如果有多条 Kaplan-Meier 曲线，可以通过比较它们来了解不同组别之间的生存差异。例如，不同治疗组或不同疾病分期的患者可能会展现出不同的生存曲线。

• 置信区间： 曲线附近会有阴影区域，表示曲线的不确定性，称为生存曲线的置信区间。置信区间越窄，表示对生存概率的估计越精确。

• 截断点： 曲线的终点可能表示研究的最后时间点，如果曲线没有到达 0% 生存概率，这意味着在研究结束时仍有患者幸存。

• 事件表： 在 Kaplan-Meier 曲线图旁，通常还会提供与之关联的事件表，其中包含每个时间点的生存概率、标准误差、事件数等信息。

3.3 额外补充

在观察上述的曲线时候，我们有时候可能想要观察某个特殊点的值和具体的事件表。以下是具体的操作代码：

打印事件表

# 打印事件表
event_table = kmf.event_table
print(f"\n事件表：\n{event_table}")

1
2
3
4

运行后，结果如下，包含了在每个时间点的被移除数、观察数、被截尾数等信息。

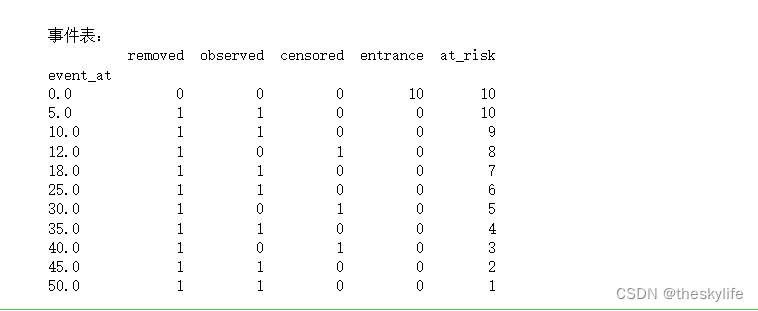
打印具体数值

# 打印详细的概率表(即生存函数)
print(f"生存曲线概率表:\n\n{kmf.survival_function_}")

# 打印某个点的概率

# 假设t = 40
t = 40
# 引用上述表中的数据
print(f"\n在时间点 {t}，生存概率为: { kmf.survival_function_.loc[t,'KM_estimate']:.2%}")
# 调用函数默认方法
print(f"\n在时间点 {t}，生存概率如下:\n { kmf.survival_function_at_times(t)}")
1
2
3
4
5
6
7
8
9
10
11

运行后，结果如下：

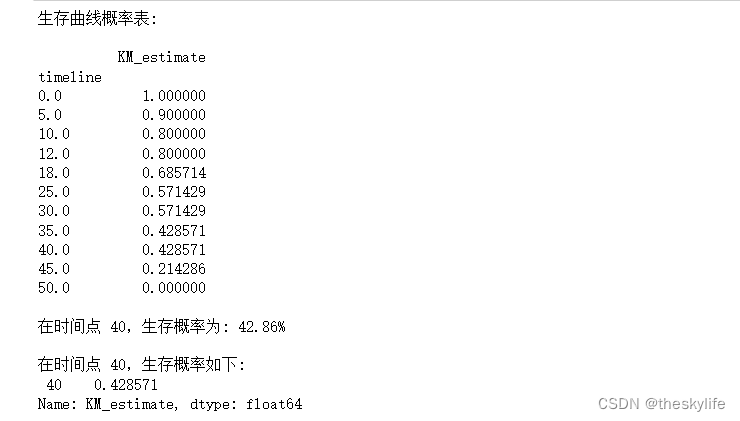
通过以上的代码，我们可以很方便的查看在具体时间点的情况。

4. Cox 比例风险模型

Cox比例风险模型是生存分析中的关键工具，允许研究人员评估不同因素对事件风险的相对影响。在这里，我们将深入了解在Python中使用lifelines库建立和训练Cox模型的过程，以及如何解释模型的输出结果。

4.1 lifelines 中的 Cox 模型

Cox比例风险模型是由统计学家David R. Cox于1972年提出的，用于分析生存数据。它是一种半参数模型，能够同时考虑时间和其他因素，如不同的变量，对事件发生的风险进行建模。在lifelines库中，我们可以方便地利用Cox模型进行生存分析，研究不同危险因素的影响。

4.1.1 数学公式

Cox模型假设不同个体的风险相对大小是恒定的，即风险的比例在整个时间范围内保持不变。Cox模型的基本形式如下：

$$h(t,\mathbf{X})=h_0(t)\exp ({\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_p{X}_p)$$

其中：

• $h(t,\mathbf{X})$ 是时间 t 的风险函数，表示在给定协变量 $\mathbf{X}$ 下的风险。
• $h_0(t)$ 是基准风险函数（baseline hazard function），表示在协变量 $\mathbf{X}=0$（所有协变量取零值）时的风险。
• ${\beta }_1,{\beta }_2,\dots ,{\beta }_p$ 是协变量的系数。
• $X_1,X_2,\dots ,X_p$ 是观测到的协变量。

4.1.2 Cox模型的应用

应用场景：

• 医学研究： 用于确定不同治疗方案对生存时间的影响。
• 人力资源： 用于预测员工离职的风险，考虑到不同的影响因素。
• 金融风险： 用于评估不同因素对投资组合的风险的影响。

注意事项：

• 比例风险假设： Cox模型建立在比例风险假设下，即变量的效应是随时间恒定的。
• 共线性： 需要注意变量之间的共线性，可能导致参数估计不准确。

4.1.3 在 lifelines 中建立和训练 Cox 模型

在建立Cox模型时，我们需要准备生存数据，并使用lifelines库中的CoxPHFitter类。该类允许我们拟合Cox模型，考察不同变量对事件风险的影响。以下是一个基本的建模步骤：

import pandas as pd
import numpy as np
from lifelines import CoxPHFitter

# 设置随机种子以确保可复现性
np.random.seed(12)

# 构建模拟数据集
data = pd.DataFrame({
    'Age': np.random.normal(50, 10, 100),
    'Treatment': np.random.choice(['A', 'B'], size=100),
    'SurvivalTime': np.random.exponential(50, 100),
    'Event': np.random.choice([1, 0], size=100)
})
# 创建 Cox 模型对象
cox_model = CoxPHFitter()

# 拟合模型并传入数据
cox_model.fit(data, duration_col='SurvivalTime', event_col='Event', formula='Age + Treatment')

# 查看模型的摘要信息
cox_model.print_summary()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

在这个过程中，我们使用了生存数据，其中包括时间（duration_col）和事件发生信息（event_col）。模型通过formula参数指定了需要考虑的变量，以及它们与事件风险的关系。

4.2 模型解释与结果分析

4.2.1 解释 Cox 模型的输出

模型的输出通常包括估计的系数、标准误差、置信区间等信息。这些信息可以帮助我们理解不同变量对事件风险的相对影响。系数的正负表示影响的方向，而系数的大小表示影响的强度。标准误差和置信区间则提供了估计的不确定性范围。

4.2.2 变量之间的关系与决策支持

深入分析模型结果有助于揭示不同变量之间的关系，进而为决策提供更全面的信息。我们可以探讨变量之间的交互效应，识别重要的预测因子，并基于模型结果制定决策策略。通过对模型进行灵活的解释和分析，我们能够更好地理解生存数据背后的故事，为实际问题提供有力的支持。

4.2.3 实例解读

运行4.1.3中的python代码后，我们可以得到下面的输出：

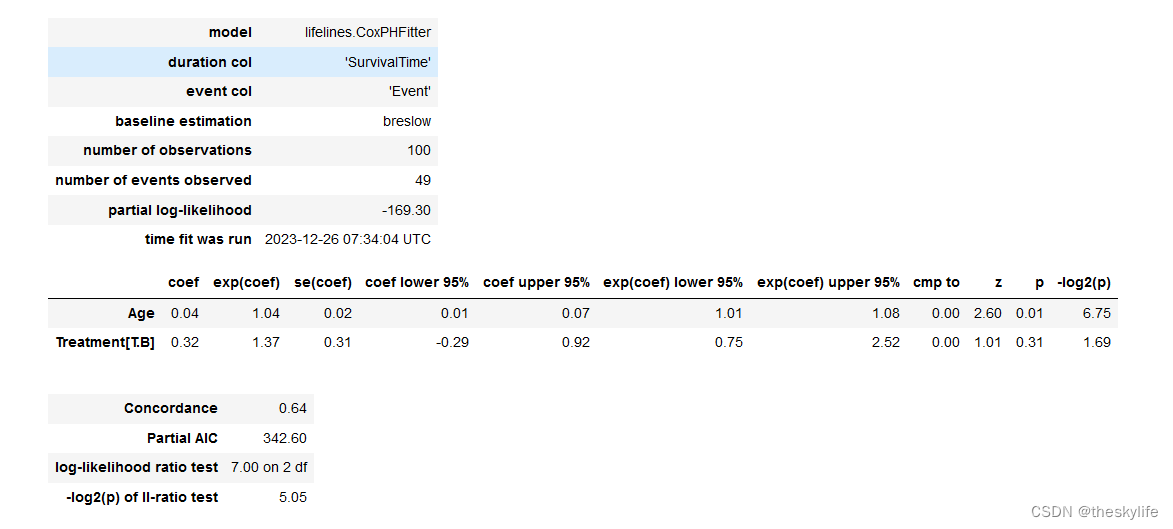
从上面的结果截图中，我们可以逐个进行解析：
让我们逐步解读这个Cox比例风险模型的输出：

• 模型信息：

  • model: 使用的生存分析模型，这里是CoxPHFitter。
  • duration col: 表示观察的时间列，这里是 ‘SurvivalTime’。
  • event col: 表示事件发生的列，这里是 ‘Event’。
  • baseline estimation: 基线生存函数的估计方法，这里是 Breslow 方法。
  • number of observations: 观察到的样本数，这里是 100。
  • number of events observed: 观察到的事件数，这里是 49。
  • partial log-likelihood: 部分对数似然，这里是 -169.30。
  • time fit was run: 模型拟合的时间，这里是 2023-12-26 07:34:04 UTC。

• 变量的系数及其统计信息：

  • Age: 年龄的系数为 0.04，95% 置信区间为 (0.01, 0.07)。风险比为 1.04，表示每增加一单位年龄，事件风险提高 4%。
  • Treatment[T.B]: 对应治疗类型B的系数为 0.32，95% 置信区间为 (-0.29, 0.92)。风险比为 1.37，表示相对于治疗类型A，治疗类型B的患者事件风险提高 37%。

• 模型评估指标：

  • Concordance: Concordance指数，表示模型预测的一致性，这里是 0.64，范围从0到1，越接近1表示模型越好。这里指数为0.64，接近于0.05，表示模型在预测患者生存时间的排序方面的准确性较低。
  • Partial AIC: 部分AIC，是AIC的一种形式，用于模型比较，越小越好。这里是 342.60，可能表示模型相对于其他模型的拟合效果较差。
  • log-likelihood ratio test: 对数似然比检验，用于比较两个模型，这里是 7.00 on 2 df，说明包含的变量对模型的改进是显著的。
  • -log2(p) of ll-ratio test: 对数似然比检验的 p 值的负对数的二进制对数，这里是 5.05，越大表示p值越小，即模型中的变量对解释事件风险的改进越显著。

• 解读：

  • 年龄（Age）的系数为 0.04，95% 置信区间为 (0.01, 0.07)，95% 置信区间不包含0，说明在统计学上 Age 的系数是显著的。其系数为正，表示随着年龄增长，事件风险有所增加。
  • Treatment[T.B]的系数为 0.32，95% 置信区间为 (-0.29, 0.92)，95% 置信区间包含0，说明在统计学上 Treatment[T.B] 的系数不是显著的，我们无法确定治疗类型B相对于治疗类型A的效应是否显著。

总体而言，模型的Concordance指数较低，表明模型对于事件发生的预测有待提升。对数似然比检验的结果显示，模型中的变量对解释事件风险是显著的。

5.Nelson-Aalen累积风险估计

Nelson-Aalen Estimator（或称为Nelson-Aalen累积风险估计器）是一种用于估计累积风险函数（cumulative hazard function）的非参数方法，常用于生存分析中。它是由David A. Nelson和Werner F. Aalen于1973年独立提出的。

5.1 Nelson-Aalen累积风险估计概念

在生存分析中，我们通常关注事件发生的时间，例如患者死亡、设备故障等。累积风险函数是一个描述时间内事件发生累积次数的函数，其值越高表示在给定时间点之前事件发生的次数越多。

5.1.1 数学公式

Nelson-Aalen Estimator的核心思想是通过观察在每个事件发生时，累积风险如何增加来估计累积风险函数。具体而言，对于每个事件发生的时间点 t，Nelson-Aalen Estimator通过以下方式计算：

$$\hat{H}(t)=\sum _{t_i\le t}\frac{d_i}{n_i}$$

其中：

• $\hat{H}(t)$ 是在时间 t 处的累积风险估计值。
• $t_i$ 是每个事件发生的时间。
• $d_i$ 是在时间 $t_i$ 处发生的事件数。
• $n_i$ 是在时间 $t_i$ 处处于风险状态的个体数（尚未发生事件或在该时间点存活的个体数）。

5.1.2 应用和注意事项

Nelson-Aalen Estimator的优点是它是一种非参数方法，不对基础分布作出假设。这使得它适用于各种生存分析的场景，特别是在面对复杂的风险情境或数据分布不明确的情况下。

应用场景：

• 设备可靠性： 用于评估设备在运行中的故障次数的累积分布。
• 生产过程： 用于估计产品质量问题的累积发生率。
• 金融领域： 用于估计不同投资的累积风险。

注意事项：

• 非参数方法： Nelson-Aalen估计器是一种非参数方法，不依赖于对分布的假设。
• 样本大小： 对于小样本，估计可能不够准确。

5.2 利用lifelines建立Nelson-Aalen累积风险估计

采用本章节2.1中的数据进行构建模型：

from lifelines import NelsonAalenFitter

# 创建NelsonAalenFitter对象
naf = NelsonAalenFitter()

# 输入生存时间和事件发生情况数据
naf.fit(durations=df['time'], event_observed=df['event'])

# 绘制累积风险曲线
naf.plot_cumulative_hazard()
plt.title('Nelson-Aalen Cumulative Hazard Curve')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

运行上述代码后，结果如下：

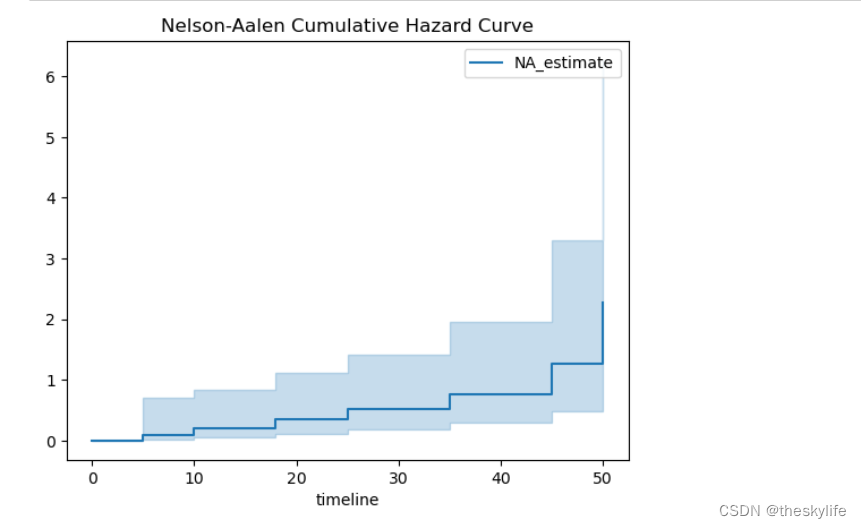
5.3 图形解释与结果分析

在查看Nelson-Aalen图形时，需要重点关注下面几项：

• 累积风险曲线： 绘制的主要曲线是累积风险曲线。该曲线显示了在不同时间点上事件的累积次数。横轴表示时间，纵轴表示累积风险。

• 事件发生的概率： 曲线上升的速度反映了事件发生的概率。如果曲线上升得较快，表示事件在该时间点上发生的概率较高。

• 曲线的变化趋势： 可以观察曲线的整体趋势，了解事件的累积分布形状。例如，曲线的斜率可能在不同的时间段上升或下降，这反映了事件发生的风险的变化。

• 时间点上的风险值： 在特定的时间点上，可以读取曲线上的数值，这表示在该时间点上事件的累积次数。这对于定量评估特定时刻的风险很有帮助。

5.4 额外补充

一般我们查阅图形时，会结合具体的数字来看，这需要借助对应的python代码：

# 打印详细的累计风险值表
# 获取累积风险估计值
cumulative_hazard_values = naf.cumulative_hazard_
print(f"生存曲线概率表:\n\n{cumulative_hazard_values}")

# 打印某个点的累计风险值

#假设t = 40
t = 40
# 引用上述表中的数据
print(f"\n在时间点 {t}，累积风险估计值为: { cumulative_hazard_values.loc[t,'NA_estimate']:.2}")
# 调用函数默认方法
print(f"\n在时间点 {t}，累积风险估计值:\n {  naf.cumulative_hazard_at_times(t)}")
1
2
3
4
5
6
7
8
9
10
11
12
13

运行上述代码后，结果如下：

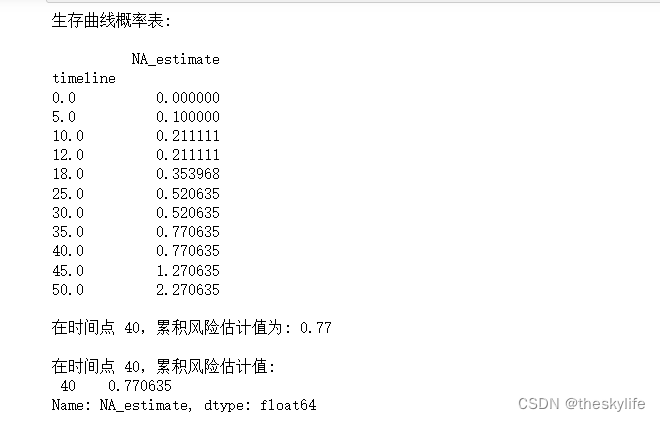
从上方图中和表中，我们可以看出在45时，上升速度较快，这说明事件在该时间点上发生的概率较高，累计有1.27单位事件发生，或者可以理解为127%概率发生。

6. 生存回归

6.1 生存回归基本概念

Survival Regression（生存回归）是生存分析（Survival Analysis）中的一种统计建模方法，它旨在探索和解释影响时间至事件发生（例如死亡、故障、疾病复发等）的因素。生存回归模型考虑到了观察到的时间数据、事件发生的状态以及可能的协变量。生存回归模型可以用于：

• 评估不同因素对于事件发生的影响。
• 预测个体的事件发生概率。
• 比较不同子组的生存曲线。
• 识别高风险群体。

常用的生存回归模型：有 Cox 模型、加速失效时间模型（Weibull 模型）、Aalen’s Additive Model 等。生存回归模型的目标是通过协变量来解释事件发生的时间。

应用场景：

• 医学研究： 用于考察患者的治疗方案随时间变化对生存的影响。
• 社会科学： 用于分析不同社会经济因素对个体生存的时间依赖性。
• 金融领域： 用于分析投资组合中资产权重随时间的变化。

注意事项：

• 时间依赖性： 适用于需要考虑时间依赖型协变量的场景。
• 样本大小： 对于小样本，需谨慎使用。

6.2 利用lifelines建立生存回归

6.2.1 方法1

使用以下类型的数据构建生存回归模型：

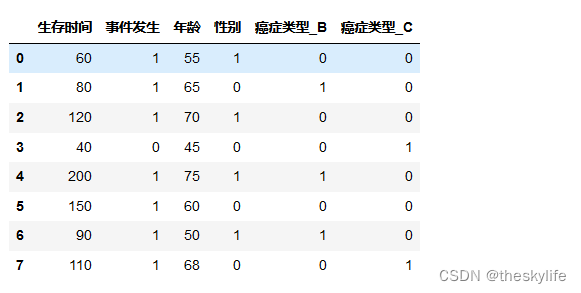
构建生存回归，需要选用对应的生存模型，这里选用cox模型：

import pandas as pd
from lifelines import CoxPHFitter

# 构建示例数据，假设有患者的生存时间、事件发生与一些协变量
data = pd.DataFrame({
    '生存时间': [60, 80, 120, 40, 200, 150, 90, 110],
    '事件发生': [1, 1, 1, 0, 1, 1, 1, 1],
    '年龄': [55, 65, 70, 45, 75, 60, 50, 68],
    '性别': [1, 0, 1, 0, 1, 0, 1, 0],  # 1表示男性，0表示女性
    '癌症类型': ['A', 'B', 'A', 'C', 'B', 'A', 'B', 'C'],
    # 可以包含更多的协变量...
})

# 对分类变量进行独热编码
data = pd.get_dummies(data, columns=['癌症类型'], drop_first=True)

# 创建CoxPHFitter对象
cph = CoxPHFitter()

# 输入生存时间、事件发生和协变量数据
cph.fit(data, duration_col='生存时间', event_col='事件发生', formula='年龄 + 性别')

# 打印模型的参数
print(cph.summary)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

运行上述代码后，结果如下：

从上方输出的模型概要，我们可以得出模型构建的效果并不好，下一步可以考虑优化模型。如果模型构建的比较出色的话，我们可以进行下一步操作。

下一步操作：

# 预测个体在 t=50 时的生存概率
test_data = pd.DataFrame({'年龄': [60, 64], '性别': [0, 1]})
predicted_survival = cph.predict_survival_function(test_data, times=[50])
print(predicted_survival)
# 比较不同组的生存曲线
ctv.plot()

1
2
3
4
5
6
7

6.2.2 方法2

使用如下类型的数据构建生存回归模型，选用cox模型：

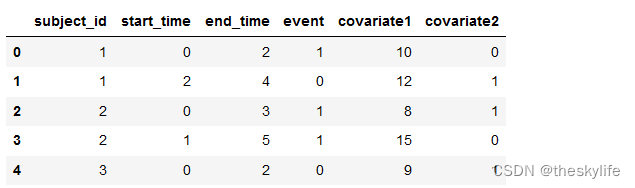
具体代码如下：

import pandas as pd
from lifelines import CoxTimeVaryingFitter

# 构建示例数据集
data = pd.DataFrame({
    'subject_id': [1, 1, 2, 2, 3],
    'start_time': [0, 2, 0, 1, 0],
    'end_time': [2, 4, 3, 5, 2],
    'event': [1, 0, 1, 1, 0],
    'covariate1': [10, 12, 8, 15, 9],
    'covariate2': [0, 1, 1, 0, 1],
})

# 创建 CoxTimeVaryingFitter 对象
# ctv = CoxTimeVaryingFitter()
ctv = CoxTimeVaryingFitter(penalizer=0.1)  # 通过调整 penalizer 的值来进行正则化


# 拟合模型
ctv.fit(data,
        id_col='subject_id',
        event_col='event',
        start_col='start_time',
        stop_col='end_time',
        formula='covariate1 + covariate2')
# 查看模型参数
print(ctv.summary)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

从上方输出的模型概要，我们可以得出模型构建的效果并不好，下一步可以考虑优化模型。如果模型构建的比较出色的话，我们可以进行下一步操作。

下一步操作：

# 新的数据用于预测
new_data = pd.DataFrame({
    'subject_id': [4, 5],
    'start_time': [1, 0],
    'end_time': [4, 3],
    'covariate1': [11, 14],
    'covariate2': [1, 0],
})

# 预测部分风险
partial_hazard = ctv.predict_partial_hazard(new_data)
print(partial_hazard)
# 比较不同组的生存曲线
ctv.plot()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

写在最后

生存分析作为数据科学领域的重要分支，为我们提供了洞察事件发生的时间与概率的独特视角。通过本文的学习，你将不仅熟悉lifelines库的使用，还能在实际问题中灵活运用生存分析方法。在下一篇文章中，我们将进一步深入，探讨更复杂的生存分析技术和案例，为数据科学的探索之路添砖加瓦。