devbox
小小林熬夜学编程
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Java学习第二十三天 图论（广度优先，深度优先，最小生成树，最短路径）一_java深度优先搜索求多叉树最短路径

作者：小小林熬夜学编程 | 2024-02-27 10:33:19

赞

踩

java深度优先搜索求多叉树最短路径

图的表示

图的遍历

深度优先：连通性路径，二分图的检测，环的检测，fllodfill

广度优先：无权图的最短路径

使用图论对问题建模

欧拉路径

哈密尔顿路径 状态压缩

桥

割点

有向图算法： DAG 环检测 拓扑排序 强连通分量

最小生成树： Kruskal Prim

最短路径： Dijkstra Floyed Bellman-Ford

网络流： 最大流-最小割  Ford-Fulkerson

图的表示

图的分类

无向图 Undirected Graph

有向图 Directed Graph

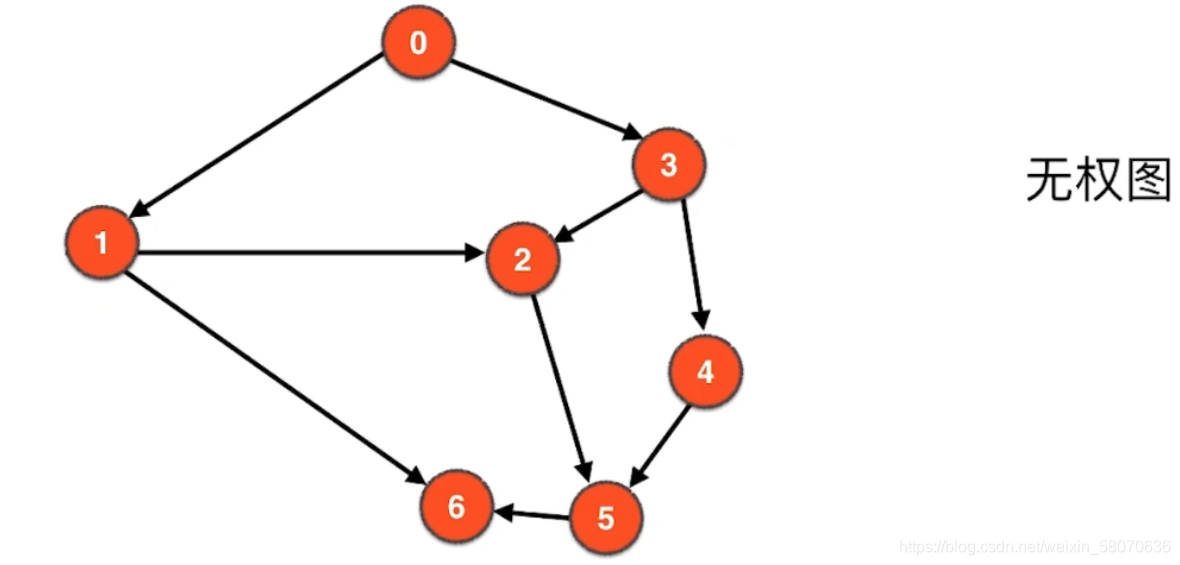
无权图

有权图

总的来说分四类

图的基本概念

无向无权图

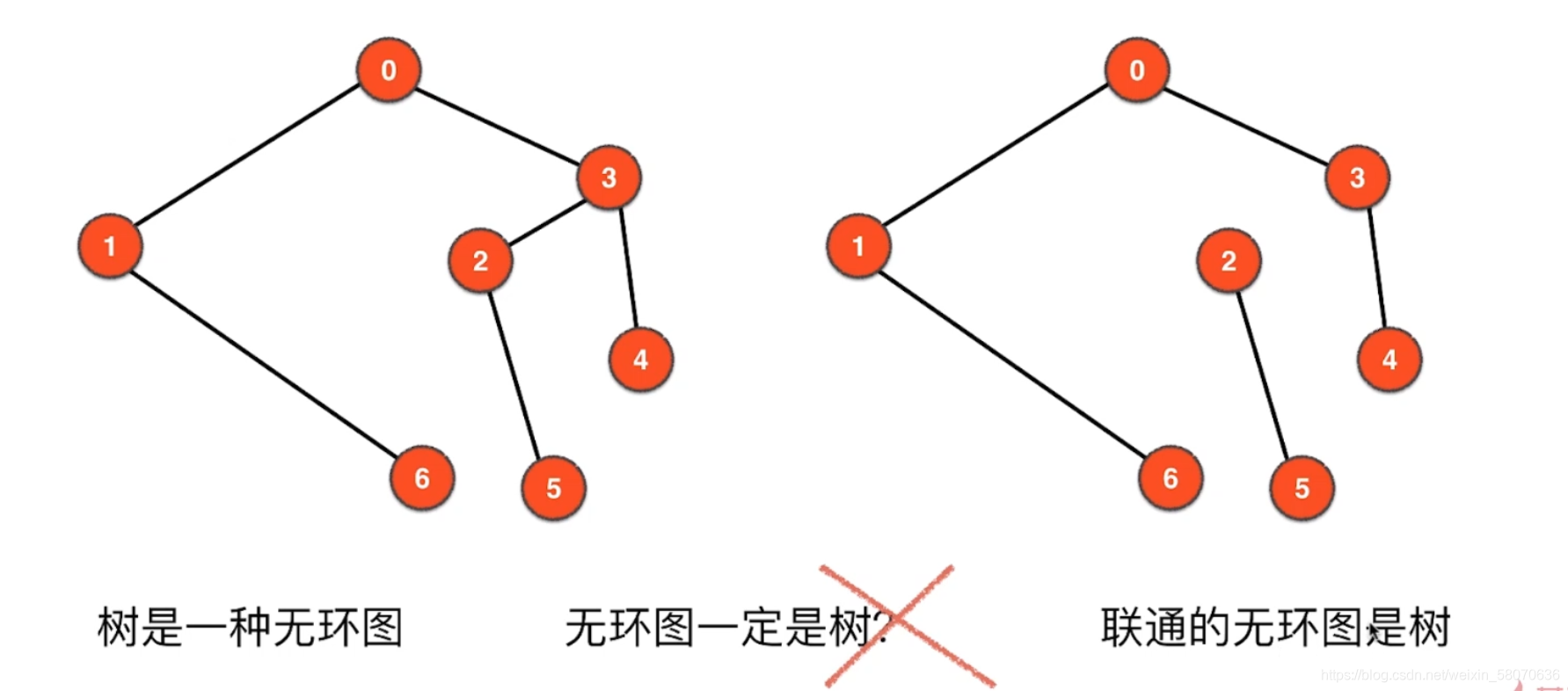
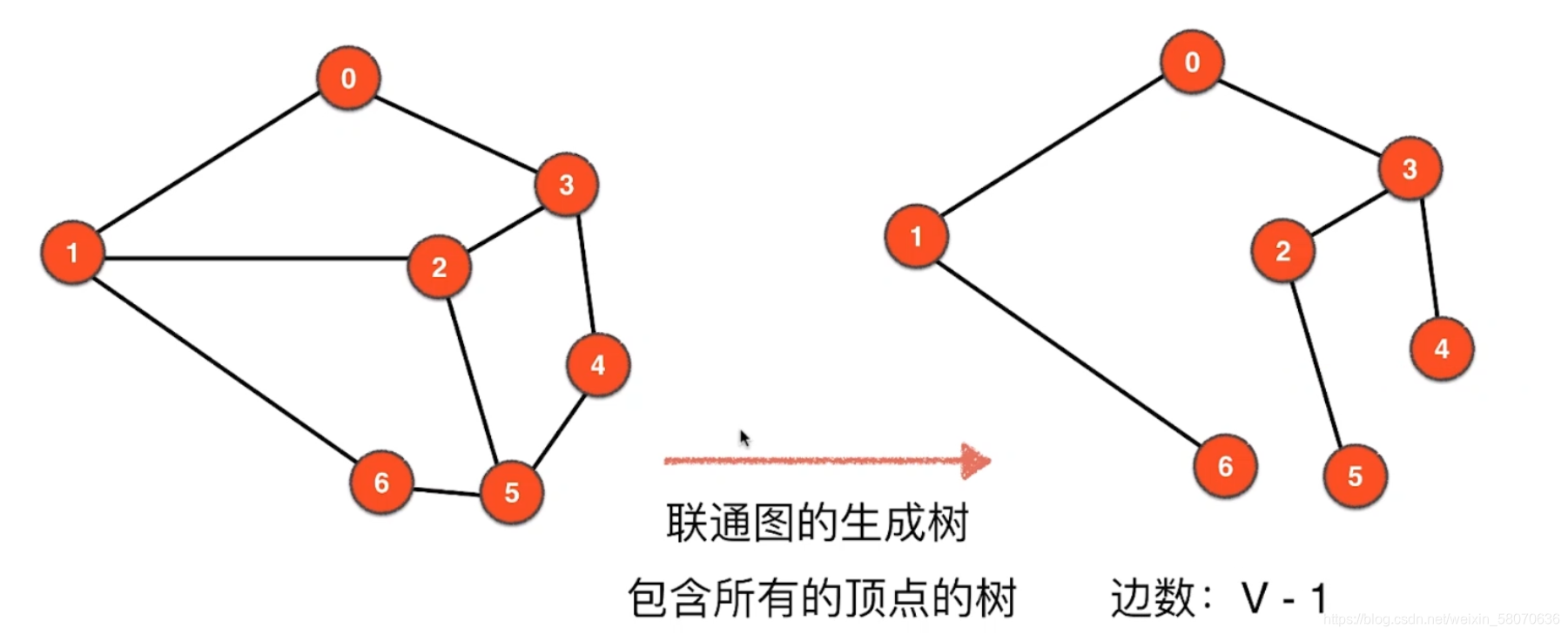
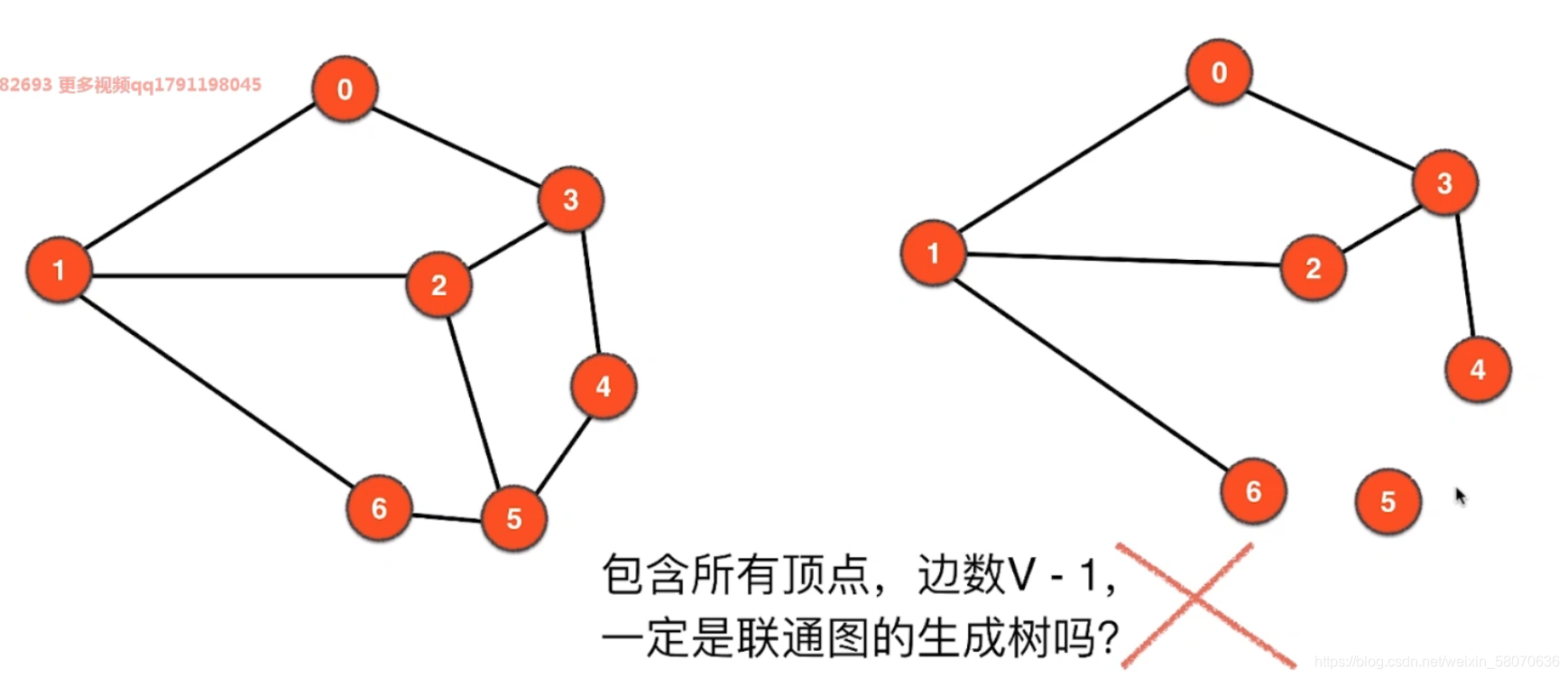
邻接矩阵

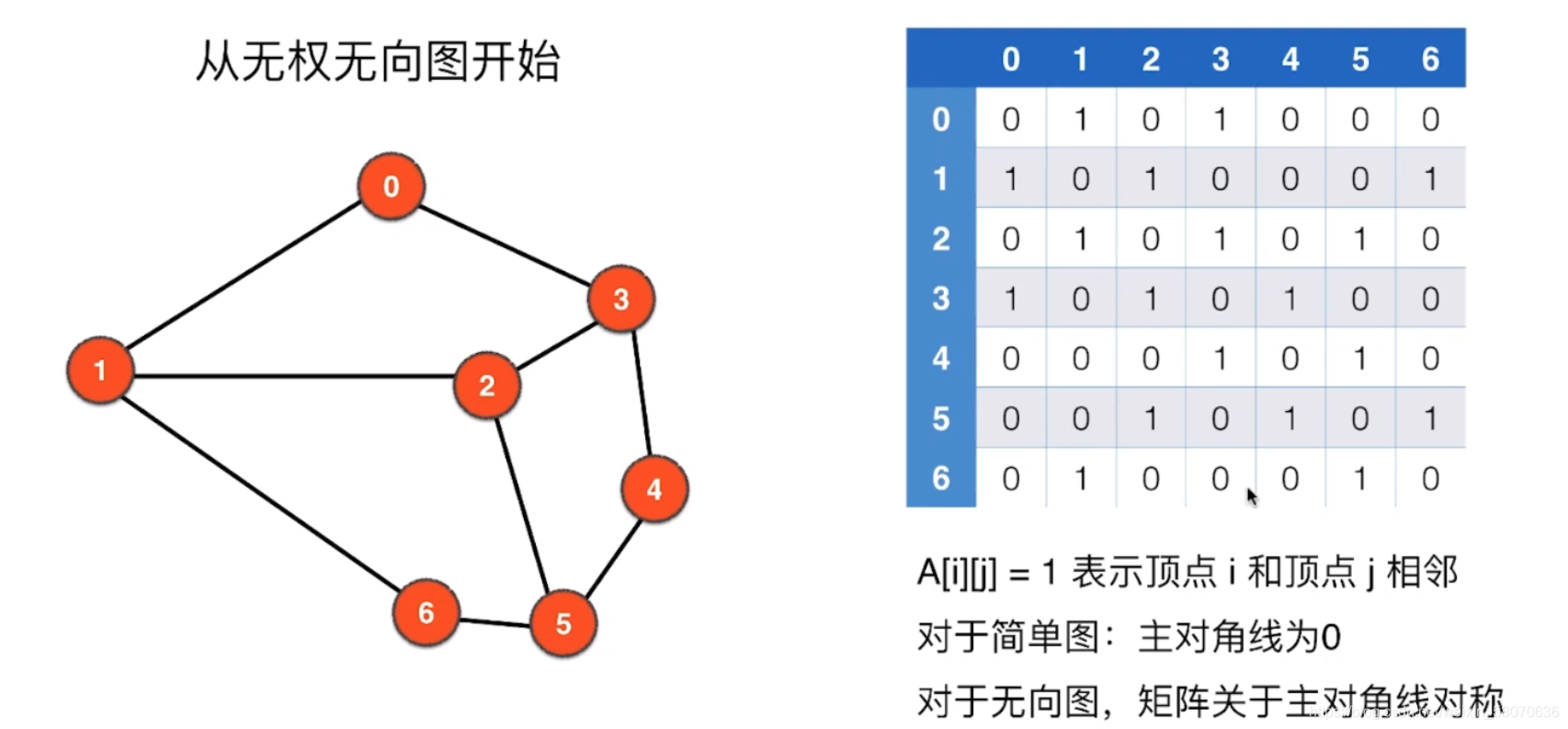
01表示在0-1之间存在一条边，以此类推

  1. package com.graph.adjacencyMatrix;
  2.  
  3. import java.io.*;//为了使用File类和异常抛出
  4. import java.util.ArrayList;
  5. import java.util.Scanner;//为了读取File里面的内容
  6.  
  7. public class AdjMatrix {
  8.  
  9.     private int V;//顶点
  10.     private int E;//边
  11.     private int[][] adj;//邻接矩阵
  12.  
  13.     public AdjMatrix(String filename){
  14.  
  15.         //用绝对路径可以避免一些相对路径时的bug，这里他说的把“。。。”这里替换成filename就是相对路径但是会报错
  16.         File file = new File("C:/Users/81909/Desktop/JavaSE/基础语法/g.txt");
  17.  
  18.         //捕获一个异常
  19.         try(Scanner scanner = new Scanner(file)){//scanner存了file里面的内容
  20.  
  21.             V = scanner.nextInt();//根据Scanner声明时括号里的内容来决定从哪里读取一个整型数字，先读V
  22.             if(V<0) throw new IllegalArgumentException("V需要是正数");
  23.             adj = new int[V][V];//创建一个V*V的二维数组
  24.  
  25.             E = scanner.nextInt();//第二个读的是E
  26.             if(E<0) throw new IllegalArgumentException("E需要是正数");
  27.             for(int i = 0; i < E; i ++){//往矩阵里填1
  28.                 int a = scanner.nextInt();
  29.                 validateVertex(a);//判断顶点合法性
  30.                 int b = scanner.nextInt();
  31.                 validateVertex(b);
  32.  
  33.                 if(a==b) throw new IllegalArgumentException("self loop is detected");//判断是否自环边
  34.                 if(adj[a][b]==1) throw new IllegalArgumentException("paralle edges are detected");//判断是否平行边
  35.  
  36.                 adj[a][b] = 1;
  37.                 adj[b][a] = 1;
  38.             }
  39.         }
  40.         catch(IOException e){
  41.             e.printStackTrace();//栈中信息打印一下
  42.         }
  43.     }
  44.  
  45.     private void validateVertex(int v){
  46.         if(v<0||v>=V) throw new IllegalArgumentException("vertex"+v+"is invalid");
  47.     }
  48.  
  49.     public int V(){return V;};//之所以不直接把它俩定义为public，是为了不让用户修改变量
  50.     public int E(){return E;};
  51.  
  52.  
  53.     //判断两点直接是否有边
  54.     public boolean hasEdge(int v,int w){
  55.         validateVertex(v);
  56.         validateVertex(w);
  57.         return adj[v][w]==1;
  58.     }
  59.  
  60.     //返回和顶点v相邻的边
  61.     public ArrayList<Integer> adj(int v){
  62.  
  63.         validateVertex(v);
  64.         ArrayList<Integer>res=new ArrayList<>();//将和v相邻的所有顶点存到res里然后反悔哦
  65.         for (int i = 0; i < V; i++) {
  66.             if(adj[v][i]==1)
  67.                 res.add(i);
  68.         }
  69.         return res;
  70.     }
  71.  
  72.     //返回顶点相对的度
  73.     public int degree(int v){
  74.         return adj(v).size();
  75.     }
  76.  
  77.     @Override
  78.     public String toString(){
  79.         StringBuilder sb = new StringBuilder();
  80.  
  81.         sb.append(String.format("V = %d, E = %d\n", V, E));//先说有多少顶点，有多少边
  82.         for(int i = 0; i < V; i ++){
  83.             for(int j = 0; j < V; j ++)
  84.                 sb.append(String.format("%d ", adj[i][j]));//把行列式给填充进去
  85.             sb.append('\n');
  86.         }
  87.         return sb.toString();
  88.     }
  89.  
  90.     public static void main(String[] args){
  91.  
  92.         AdjMatrix adjMatrix = new AdjMatrix("g.txt");
  93.         System.out.print(adjMatrix);
  94.     }
  95. }

结果

  1. V = 7, E = 9
  2. 0 1 0 1 0 0 0 
  3. 1 0 1 0 0 0 1 
  4. 0 1 0 1 0 1 0 
  5. 1 0 1 0 1 0 0 
  6. 0 0 0 1 0 1 0 
  7. 0 0 1 0 1 0 1 
  8. 0 1 0 0 0 1 0 
  9.  
  10. Process finished with exit code 0

图的基本表示：邻接矩阵

这里树形状的空间为点的个数加边的个数就足够存下所有信息了，degree(v)也可以小于O(v)

稀疏图与稠密图

图的基本表示：邻接表

  1. package com.graph.adjacencyMatrix;
  2.  
  3. import java.util.LinkedList;//邻接表是链表
  4. import java.io.*;
  5. import java.util.Scanner;
  6.  
  7. public class AdjList {
  8.  
  9.     private int V;
  10.     private int E;
  11.     private LinkedList<Integer>[] adj;
  12.  
  13.     public AdjList(String filename){
  14.  
  15.         File file = new File("C:/Users/81909/Desktop/JavaSE/基础语法/g.txt");
  16.  
  17.         try(Scanner scanner = new Scanner(file)){
  18.  
  19.             V = scanner.nextInt();
  20.             if(V<0) throw new IllegalArgumentException("V需要是正数");
  21.             adj = new LinkedList[V];//创建一个空间为V的链表
  22.             for (int i = 0; i < V; i++) {
  23.                 adj[i]=new LinkedList<Integer>();//为每一个元素申请空间，不写Integer这个泛型也可以
  24.             }
  25.  
  26.             E = scanner.nextInt();
  27.             if(E<0) throw new IllegalArgumentException("E需要是正数");
  28.             for(int i = 0; i < E; i ++){
  29.                 int a = scanner.nextInt();
  30.                 validateVertex(a);
  31.                 int b = scanner.nextInt();
  32.                 validateVertex(b);
  33.  
  34.                 if(a==b) throw new IllegalArgumentException("self loop is detected");
  35.                 if(adj[a].contains(b)) throw new IllegalArgumentException("paralle edges are detected");
  36.  
  37.                 adj[a].add(b);
  38.                 adj[b].add(a);
  39.             }
  40.         }
  41.         catch(IOException e){
  42.             e.printStackTrace();
  43.         }
  44.     }
  45.  
  46.     private void validateVertex(int v){
  47.         if(v<0||v>=V) throw new IllegalArgumentException("vertex"+v+"is invalid");
  48.     }
  49.  
  50.     public int V(){return V;};
  51.     public int E(){return E;};
  52.  
  53.  
  54.     //判断两点直接是否有边
  55.     public boolean hasEdge(int v,int w){
  56.         validateVertex(v);
  57.         validateVertex(w);
  58.         return adj[v].contains(w);
  59.     }
  60.  
  61.     //返回和顶点v相邻的边
  62.     public LinkedList<Integer> adj(int v){
  63.  
  64.         validateVertex(v);
  65.         return adj[v];
  66.     }
  67.  
  68.     //返回顶点相对的度
  69.     public int degree(int v){
  70.         return adj(v).size();
  71.     }
  72.  
  73.     @Override
  74.     public String toString(){
  75.         StringBuilder sb = new StringBuilder();
  76.  
  77.         sb.append(String.format("V = %d, E = %d\n", V, E));//先说有多少顶点，有多少边
  78.         for(int v = 0; v < V; v ++){
  79.             sb.append(String.format("%d:",v));//每一轮v相邻的顶点都有谁
  80.             for(int w:adj[v])
  81.                 sb.append(String.format("%d ", w));//把行列式给填充进去
  82.             sb.append('\n');
  83.         }
  84.         return sb.toString();
  85.     }
  86.  
  87.     public static void main(String[] args){
  88.  
  89.         AdjList adjList = new AdjList("g.txt");
  90.         System.out.print(adjList);
  91.     }
  92. }

结果

  1. V = 7, E = 9
  2. 0:1 3 
  3. 1:0 2 6 
  4. 2:1 3 5 
  5. 3:0 2 4 
  6. 4:3 5 
  7. 5:2 4 6 
  8. 6:1 5 
  9.  
  10. Process finished with exit code 0

邻接表的问题和改进

有的只有顶点没有边，用O(E)代替不可取

  1. package com.graph.adjacencyMatrix;
  2.  
  3. import java.io.File;
  4. import java.io.IOException;
  5. import java.util.TreeSet;
  6. import java.util.Scanner;
  7.  
  8. public class AdjSet {
  9.  
  10.     private int V;
  11.     private int E;
  12.     private TreeSet<Integer>[] adj;
  13.  
  14.     public AdjSet(String pathStr){
  15.  
  16.         File file = new File(pathStr);
  17.  
  18.         try(Scanner scanner = new Scanner(file)){
  19.  
  20.             V = scanner.nextInt();
  21.             if(V < 0) throw new IllegalArgumentException("V must be non-negative");
  22.             adj = new TreeSet[V];
  23.             for(int i = 0; i < V; i ++)
  24.                 adj[i] = new TreeSet<Integer>();
  25.  
  26.             E = scanner.nextInt();
  27.             if(E < 0) throw new IllegalArgumentException("E must be non-negative");
  28.  
  29.             for(int i = 0; i < E; i ++){
  30.                 int a = scanner.nextInt();
  31.                 validateVertex(a);
  32.                 int b = scanner.nextInt();
  33.                 validateVertex(b);
  34.  
  35.                 if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");
  36.                 if(adj[a].contains(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");
  37.  
  38.                 adj[a].add(b);
  39.                 adj[b].add(a);
  40.             }
  41.         }
  42.         catch(IOException e){
  43.             e.printStackTrace();
  44.         }
  45.     }
  46.  
  47.     private void validateVertex(int v){
  48.         if(v < 0 || v >= V)
  49.             throw new IllegalArgumentException("vertex " + v + "is invalid");
  50.     }
  51.  
  52.     public int V(){
  53.         return V;
  54.     }
  55.  
  56.     public int E(){
  57.         return E;
  58.     }
  59.  
  60.     public boolean hasEdge(int v, int w){
  61.         validateVertex(v);
  62.         validateVertex(w);
  63.         return adj[v].contains(w);
  64.     }
  65.  
  66.     public Iterable<Integer> adj(int v){
  67.         // public TreeSet<Integer> adj(int v){
  68.         validateVertex(v);
  69.         return adj[v];
  70.     }
  71.  
  72.     public int degree(int v){
  73.         validateVertex(v);
  74.         return adj[v].size();
  75.     }
  76.  
  77.     @Override
  78.     public String toString(){
  79.         StringBuilder sb = new StringBuilder();
  80.  
  81.         sb.append(String.format("V = %d, E = %d\n", V, E));
  82.         for(int v = 0; v < V; v ++){
  83.             sb.append(String.format("%d : ", v));
  84.             for(int w : adj[v])
  85.                 sb.append(String.format("%d ", w));
  86.             sb.append('\n');
  87.         }
  88.         return sb.toString();
  89.     }
  90.  
  91.     public static void main(String[] args){
  92.  
  93.         AdjSet adjSet = new AdjSet("g.txt");
  94.         System.out.print(adjSet);
  95.     }
  96. }

图的基本表示比较

遍历的意义

很多算法的本质都是遍历，对图论问题来说，绝大部分问题都依托于遍历

图的深度优先遍历

树与图的优先遍历比较

实现图的深度优先遍历

  1. package com.graph.GraphDFS;
  2.  
  3. import java.util.ArrayList;
  4.  
  5. public class GraphDFS {
  6.  
  7.     private Graph G;
  8.     private boolean[] visited;
  9.  
  10.     private ArrayList<Integer> order = new ArrayList<>();
  11.  
  12.     public GraphDFS(Graph G){//构造函数
  13.  
  14.         this.G = G;
  15.         visited = new boolean[G.V()];//图中每一个顶点对应一个visited记录值
  16.         dfs(0);
  17.     }
  18.  
  19.     //递归遍历
  20.     private void dfs(int v){
  21.  
  22.         visited[v] = true;
  23.         order.add(v);
  24.         for(int w: G.adj(v))
  25.             if(!visited[w])
  26.                 dfs(w);
  27.     }
  28.  
  29.     public Iterable<Integer> order(){
  30.         return order;
  31.     }
  32.  
  33.     public static void main(String[] args){
  34.  
  35.         Graph g = new Graph("C:/Users/81909/Desktop/JavaSE/基础语法/g.txt");
  36.         GraphDFS graphDFS = new GraphDFS(g);
  37.         System.out.println(graphDFS.order());
  38.     }
  39. }

结果

[0, 1, 3, 2, 6, 5, 4]

  1. package com.graph.GraphDFS;
  2.  
  3. import java.util.ArrayList;
  4.  
  5. public class GraphDFS {
  6.  
  7.     private Graph G;
  8.     private boolean[] visited;
  9.  
  10.     private ArrayList<Integer> order = new ArrayList<>();
  11.  
  12.     public GraphDFS(Graph G){//构造函数
  13.  
  14.         this.G = G;
  15.         visited = new boolean[G.V()];//图中每一个顶点对应一个visited记录值
  16.         for (int v = 0; v < G.V(); v++) {
  17.             if(!visited[v])
  18.             dfs(v);
  19.         }
  20.  
  21.     }
  22.  
  23.     //递归遍历
  24.     private void dfs(int v){
  25.  
  26.         visited[v] = true;
  27.         order.add(v);
  28.         for(int w: G.adj(v))
  29.             if(!visited[w])
  30.                 dfs(w);
  31.     }
  32.  
  33.     public Iterable<Integer> order(){
  34.         return order;
  35.     }
  36.  
  37.     public static void main(String[] args){
  38.  
  39.         Graph g = new Graph("C:/Users/81909/Desktop/JavaSE/基础语法/g.txt");
  40.         GraphDFS graphDFS = new GraphDFS(g);
  41.         System.out.println(graphDFS.order());
  42.     }
  43. }

对象与结果

  1. 7 6
  2. 0 1
  3. 0 2
  4. 1 3
  5. 1 4
  6. 2 3
  7. 2 6
  8.  
  9.  
  10. [0, 1, 3, 2, 6, 4, 5]

二叉树的遍历

图的遍历

  1. package com.graph.GraphDFS;
  2.  
  3. import java.util.ArrayList;
  4.  
  5. public class GraphDFS {
  6.  
  7.     private Graph G;
  8.     private boolean[] visited;
  9.  
  10.     private ArrayList<Integer> pre = new ArrayList<>();
  11.     private ArrayList<Integer> post = new ArrayList<>();
  12.  
  13.     public GraphDFS(Graph G){//构造函数
  14.  
  15.         this.G = G;
  16.         visited = new boolean[G.V()];//图中每一个顶点对应一个visited记录值
  17.         for (int v = 0; v < G.V(); v++) {
  18.             if(!visited[v])
  19.             dfs(v);
  20.         }
  21.  
  22.     }
  23.  
  24.     //递归遍历
  25.     private void dfs(int v){
  26.  
  27.         visited[v] = true;
  28.         pre.add(v);
  29.         for(int w: G.adj(v))
  30.             if(!visited[w])
  31.                 dfs(w);
  32.  
  33.             post.add(v);
  34.     }
  35.  
  36.     public Iterable<Integer> pre(){
  37.         return pre;
  38.     }
  39.  
  40.     public Iterable<Integer> post(){
  41.         return post;
  42.     }
  43.  
  44.     public static void main(String[] args){
  45.  
  46.         Graph g = new Graph("C:/Users/81909/Desktop/JavaSE/基础语法/g.txt");
  47.         GraphDFS graphDFS = new GraphDFS(g);
  48.         System.out.println(graphDFS.pre());
  49.         System.out.println(graphDFS.post());
  50.     }
  51. }

结果

  1. [0, 1, 3, 2, 6, 4, 5]
  2. [6, 2, 3, 4, 1, 0, 5]

深度优先遍历复杂度：O(V+E)

深度优先遍历的应用

无向图的联通分量Connected Component

无向图的联通分量个数

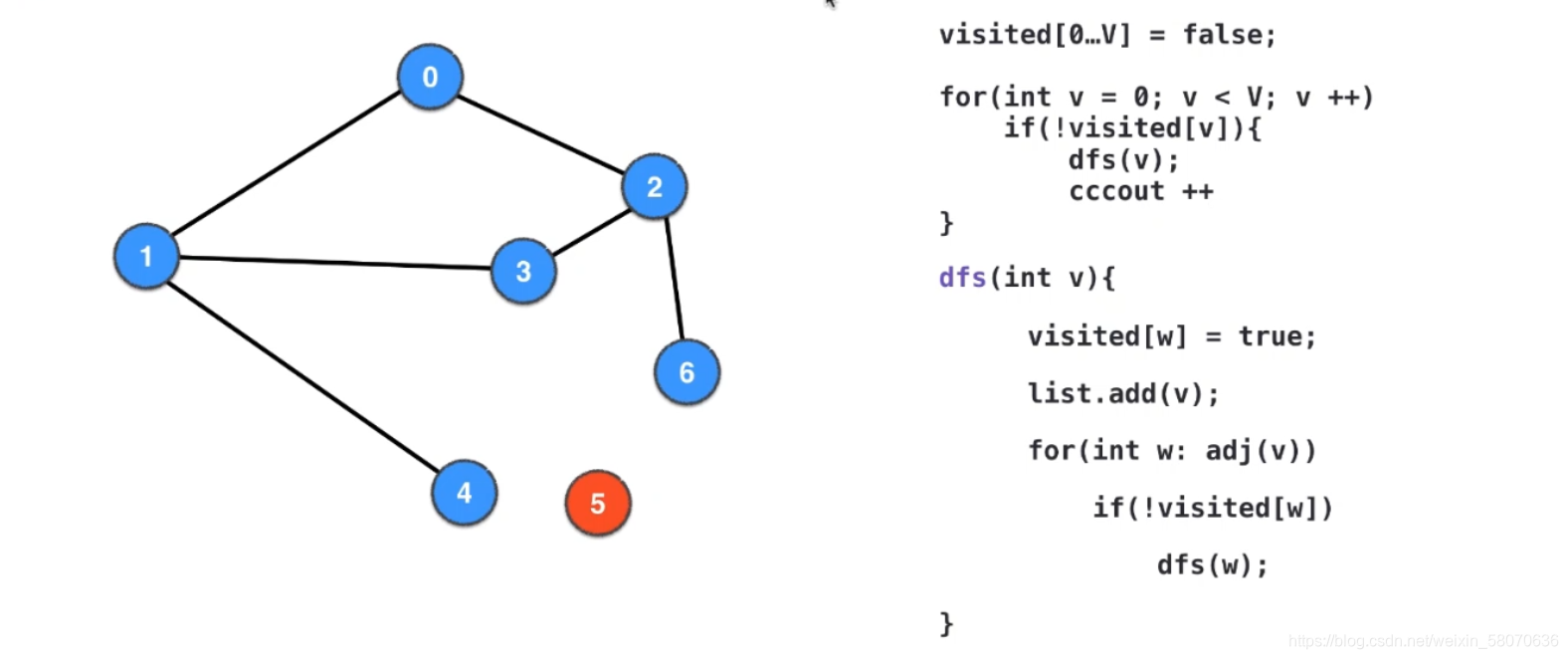
具体求解无向图的联通分量

更进一步

  1. import java.util.ArrayList;
  2.  
  3. public class CC {
  4.  
  5.     private Graph G;
  6.     private int[] visited;
  7.     private int cccount = 0;
  8.  
  9.     public CC(Graph G){
  10.  
  11.         this.G = G;
  12.         visited = new int[G.V()];
  13.         for(int i = 0; i < visited.length; i ++)
  14.             visited[i] = -1;
  15.  
  16.         for(int v = 0; v < G.V(); v ++)
  17.             if(visited[v] == -1){
  18.                 dfs(v, cccount);
  19.                 cccount ++;
  20.             }
  21.     }
  22.  
  23.     private void dfs(int v, int ccid){
  24.  
  25.         visited[v] = ccid;
  26.         for(int w: G.adj(v))
  27.             if(visited[w] == -1)
  28.                 dfs(w, ccid);
  29.     }
  30.  
  31.     public int count(){
  32. //        for(int e: visited)
  33. //            System.out.print(e + " ");
  34. //        System.out.println();
  35.         return cccount;
  36.     }
  37.  
  38.     //判断俩顶点是否在一个联通分量里面
  39.     public boolean isConnected(int v, int w){
  40.         G.validateVertex(v);
  41.         G.validateVertex(w);
  42.         return visited[v] == visited[w];
  43.     }
  44.  
  45.     //返回每张图有多少联通分量，每个联通分量对应的顶点分别是谁
  46.     public ArrayList<Integer>[] components(){
  47.  
  48.         ArrayList<Integer>[] res = new ArrayList[cccount];
  49.         for(int i = 0; i < cccount; i ++)
  50.             res[i] = new ArrayList<Integer>();
  51.  
  52.         for(int v = 0; v < G.V(); v ++)
  53.             res[visited[v]].add(v);
  54.         return res;
  55.     }
  56.  
  57.     public static void main(String[] args){
  58.  
  59.         Graph g = new Graph("g.txt");
  60.         CC cc = new CC(g);
  61.         System.out.println(cc.count());
  62.  
  63.         System.out.println(cc.isConnected(0, 6));
  64.         System.out.println(cc.isConnected(5, 6));
  65.  
  66.         ArrayList<Integer>[] comp = cc.components();
  67.         for(int ccid = 0; ccid < comp.length; ccid ++){
  68.             System.out.print(ccid + " : ");
  69.             for(int w: comp[ccid])
  70.                 System.out.print(w + " ");
  71.             System.out.println();
  72.         }
  73.     }
  74. }

路径问题

  1. import java.util.ArrayList;
  2. import java.util.Collections;
  3.  
  4. public class SingleSourcePath {
  5.  
  6.     private Graph G;
  7.     private int s;
  8.  
  9.     private boolean[] visited;
  10.     private int[] pre;
  11.  
  12.     public SingleSourcePath(Graph G, int s){
  13.  
  14.         G.validateVertex(s);
  15.  
  16.         this.G = G;
  17.         this.s = s;
  18.         visited = new boolean[G.V()];
  19.         pre = new int[G.V()];
  20.  
  21.         dfs(s, s);
  22.     }
  23.  
  24.     private void dfs(int v, int parent){
  25.  
  26.         visited[v] = true;
  27.         pre[v] = parent;
  28.         for(int w: G.adj(v))
  29.             if(!visited[w])
  30.                 dfs(w, v);
  31.     }
  32.  
  33.     //判断是不是和源在一起
  34.     public boolean isConnectedTo(int t){
  35.         G.validateVertex(t);
  36.         return visited[t];
  37.     }
  38.  
  39.     //输出路径
  40.     public Iterable<Integer> path(int t){
  41.  
  42.         ArrayList<Integer> res = new ArrayList<Integer>();
  43.         if(!isConnectedTo(t)) return res;//不能到达路径就返回空路径
  44.  
  45.         int cur = t;
  46.         while(cur != s){
  47.             res.add(cur);
  48.             cur = pre[cur];
  49.         }
  50.         res.add(s);
  51.  
  52.         Collections.reverse(res);//颠倒过来，返回正序
  53.         return res;
  54.     }
  55.  
  56.     public static void main(String[] args){
  57.  
  58.         Graph g = new Graph("g.txt");
  59.         SingleSourcePath sspath = new SingleSourcePath(g, 0);
  60.         System.out.println("0 -> 6 : " + sspath.path(6));
  61.         System.out.println("0 -> 5 : " + sspath.path(5));
  62.     }
  63. }

点对点路径问题

  1. import java.util.ArrayList;
  2. import java.util.Collections;
  3.  
  4. public class Path {
  5.  
  6.     private Graph G;
  7.     private int s, t;
  8.  
  9.     private int[] pre;
  10.     private boolean[] visited;
  11.  
  12.     public Path(Graph G, int s, int t){//源点与终止点
  13.  
  14.         G.validateVertex(s);
  15.         G.validateVertex(t);
  16.  
  17.         this.G = G;
  18.         this.s = s;
  19.         this.t = t;
  20.  
  21.         visited = new boolean[G.V()];
  22.         pre = new int[G.V()];
  23.         for(int i = 0; i < pre.length; i ++)
  24.             pre[i] = -1;
  25.  
  26.         dfs(s, s);
  27.         for(boolean e: visited)
  28.             System.out.print(e + " ");
  29.         System.out.println();
  30.     }
  31.  
  32.     private boolean dfs(int v, int parent){
  33.  
  34.         visited[v] = true;
  35.         pre[v] = parent;
  36.  
  37.         if(v == t) return true;
  38.  
  39.         for(int w: G.adj(v))
  40.             if(!visited[w])
  41.                 if(dfs(w, v))
  42.                     return true;
  43.         return false;
  44.     }
  45.  
  46.     public boolean isConnected(){
  47.         return visited[t];
  48.     }
  49.  
  50.     public Iterable<Integer> path(){
  51.  
  52.         ArrayList<Integer> res = new ArrayList<Integer>();
  53.         if(!isConnected()) return res;
  54.  
  55.         int cur = t;
  56.         while(cur != s){
  57.             res.add(cur);
  58.             cur = pre[cur];
  59.         }
  60.         res.add(s);
  61.  
  62.         Collections.reverse(res);
  63.         return res;
  64.     }
  65.  
  66.     public static void main(String[] args){
  67.  
  68.         Graph g = new Graph("g.txt");
  69.         Path path = new Path(g, 0, 6);
  70.         System.out.println("0 -> 6 : " + path.path());
  71.  
  72.         Path path2 = new Path(g, 0, 5);
  73.         System.out.println("0 -> 5 : " + path2.path());
  74.  
  75.         Path path3 = new Path(g, 0, 1);
  76.         System.out.println("0 -> 1 : " + path3.path());
  77.     }
  78. }

无向图中的环检测问题

  1. public class CycleDetection {
  2.  
  3.     private Graph G;
  4.     private boolean[] visited;
  5.     private boolean hasCycle = false;
  6.  
  7.     public CycleDetection(Graph G){
  8.  
  9.         this.G = G;
  10.         visited = new boolean[G.V()];
  11.         for(int v = 0; v < G.V(); v ++)
  12.             if(!visited[v])
  13.                 if(dfs(v, v)){
  14.                     hasCycle = true;
  15.                     break;
  16.                 }
  17.     }
  18.  
  19.     // 从顶点 v 开始，判断图中是否有环
  20.     private boolean dfs(int v, int parent){
  21.  
  22.         visited[v] = true;
  23.         for(int w: G.adj(v))
  24.             if(!visited[w]){
  25.                 if(dfs(w, v)) return true;
  26.             }
  27.             else if(w != parent)
  28.                 return true;
  29.         return false;
  30.     }
  31.  
  32.     public boolean hasCycle(){
  33.         return hasCycle;
  34.     }
  35.  
  36.     public static void main(String[] args){
  37.  
  38.         Graph g = new Graph("g.txt");
  39.         CycleDetection cycleDetection = new CycleDetection(g);
  40.         System.out.println(cycleDetection.hasCycle());
  41.  
  42.         Graph g2 = new Graph("g2.txt");
  43.         CycleDetection cycleDetection2 = new CycleDetection(g2);
  44.         System.out.println(cycleDetection2.hasCycle());
  45.     }
  46. }

二分图检测

染色处理

  1. import java.util.ArrayList;
  2.  
  3. public class BipartitionDetection {
  4.  
  5.     private Graph G;
  6.  
  7.     private boolean[] visited;
  8.     private int[] colors;
  9.     private boolean isBipartite = true;
  10.  
  11.     public BipartitionDetection(Graph G){
  12.  
  13.         this.G = G;
  14.         visited = new boolean[G.V()];
  15.         colors = new int[G.V()];
  16.         for(int i = 0; i < G.V(); i ++)
  17.             colors[i] = -1;
  18.  
  19.         for(int v = 0; v < G.V(); v ++)
  20.             if(!visited[v])
  21.                 if(!dfs(v, 0)){
  22.                     isBipartite = false;
  23.                     break;
  24.                 }
  25.     }
  26.  
  27.     private boolean dfs(int v, int color){
  28.  
  29.         visited[v] = true;
  30.         colors[v] = color;
  31.         for(int w: G.adj(v))
  32.             if(!visited[w]){
  33.                 if(!dfs(w, 1 - color)) return false;
  34.             }
  35.             else if(colors[w] == colors[v])
  36.                 return false;
  37.         return true;
  38.     }
  39.  
  40.     public boolean isBipartite(){
  41.         return isBipartite;
  42.     }
  43.  
  44.     public static void main(String[] args){
  45.  
  46.         Graph g = new Graph("g.txt");
  47.         BipartitionDetection bipartitionDetection = new BipartitionDetection(g);
  48.         System.out.println(bipartitionDetection.isBipartite);
  49.         // true
  50.  
  51.         Graph g2 = new Graph("g2.txt");
  52.         BipartitionDetection bipartitionDetection2 = new BipartitionDetection(g2);
  53.         System.out.println(bipartitionDetection2.isBipartite);
  54.         // false
  55.  
  56.         Graph g3 = new Graph("g3.txt");
  57.         BipartitionDetection bipartitionDetection3 = new BipartitionDetection(g3);
  58.         System.out.println(bipartitionDetection3.isBipartite);
  59.         // true
  60.     }
  61. }

小节

图的广度优先遍历

从树的广度优先遍历到图的广度优先遍历

广度优先：对一个节点，先把所有子节点都遍历了再操作

从边遍历，只能遍历同一联通分量

需要一层外循环调用各个联通分量

  1. import java.util.ArrayList;
  2. import java.util.LinkedList;
  3. import java.util.Queue;
  4.  
  5. public class GraphBFS {
  6.  
  7.     private Graph G;
  8.     private boolean[] visited;
  9.  
  10.     private ArrayList<Integer> order = new ArrayList<>();//广度优先没有前序后序,这里order代表遍历顺序
  11.  
  12.     public GraphBFS(Graph G){
  13.  
  14.         this.G = G;
  15.         visited = new boolean[G.V()];//为visited开空间，有多少顶点就开多少个
  16.         for(int v = 0; v < G.V(); v ++)//如果从0遍历就只能遍历0所在联通分量，所以需要从所有节点开始
  17.             if(!visited[v])
  18.                 bfs(v);
  19.     }
  20.  
  21.     private void bfs(int s){
  22.  
  23.         Queue<Integer> queue = new LinkedList<>();//Queue是一个接口，所以要具体一个实践的类，这里用链表类
  24.         queue.add(s);
  25.         visited[s] = true;//入队了就visited=true
  26.         while(!queue.isEmpty()){//链表队列不为空时
  27.             int v = queue.remove();//队首取出元素v
  28.             order.add(v);//添加到order这个队列中
  29.  
  30.             for(int w: G.adj(v))//查看v顶点所有相邻顶点w
  31.                 if(!visited[w]){
  32.                     queue.add(w);//如果w没被遍历过，入队
  33.                     visited[w] = true;//设为已访问
  34.                 }
  35.         }
  36.     }
  37.  
  38.     public Iterable<Integer> order(){
  39.         return order;
  40.     }
  41.  
  42.     public static void main(String[] args){
  43.  
  44.         Graph g = new Graph("g.txt");
  45.         GraphBFS graphBFS = new GraphBFS(g);
  46.         System.out.println("BFS Order : " + graphBFS.order());
  47.     }
  48. }

复杂度：O(V+E)

使用BFS求解单源路径问题

  1. import java.util.ArrayList;
  2. import java.util.Collections;
  3. import java.util.LinkedList;
  4. import java.util.Queue;
  5.  
  6. public class SingleSourcePath {
  7.  
  8.     private Graph G;
  9.     private int s;
  10.  
  11.     private boolean[] visited;
  12.     private int[] pre;
  13.      //没有顺序问题，所以去除了BFS中的ArrayList<>order
  14.     public SingleSourcePath(Graph G, int s){//创建对象时考虑源是谁
  15.  
  16.         this.G = G;
  17.         this.s = s;
  18.  
  19.         visited = new boolean[G.V()];
  20.         pre = new int[G.V()];//路径问题，记录pre这个信息，给pre开空间
  21.         for(int i = 0; i < pre.length; i ++)//再赋初值
  22.             pre[i] = -1;
  23.  
  24.         bfs(s);//单源问题，只需要从s出发就行
  25.     }
  26.  
  27.     private void bfs(int s){
  28.  
  29.         Queue<Integer> queue = new LinkedList<>();
  30.         queue.add(s);
  31.         visited[s] = true;
  32.         pre[s] = s;
  33.         while(!queue.isEmpty()){
  34.             int v = queue.remove();
  35.  
  36.             for(int w: G.adj(v))//求v的相邻节点w
  37.                 if(!visited[w]){
  38.                     queue.add(w);
  39.                     visited[w] = true;
  40.                     pre[w] = v;//w上一个节点是v
  41.                 }
  42.         }
  43.     }
  44.  
  45.     public boolean isConnectedTo(int t){//判断是不是连接到了t节点
  46.         G.validateVertex(t);
  47.         return visited[t];
  48.     }
  49.  
  50.     public Iterable<Integer> path(int t){//求解路径
  51.  
  52.         ArrayList<Integer> res = new ArrayList<Integer>();//定义res用来之后存路径
  53.         if(!isConnectedTo(t)) return res;//到达不了t就返回空
  54.  
  55.         int cur = t;//从终值t出发，记为cur
  56.         while(cur != s){//只要还没回到起点s
  57.             res.add(cur);//往存路径的res里add一个cur
  58.             cur = pre[cur];//往前面一个点跑
  59.         }
  60.         res.add(s);//最后添加源点s
  61.  
  62.         Collections.reverse(res);//反转一下
  63.         return res;
  64.     }
  65.  
  66.     public static void main(String[] args){
  67.  
  68.         Graph g = new Graph("g.txt");
  69.         SingleSourcePath sspath = new SingleSourcePath(g, 0);
  70.         System.out.println("0 -> 6 : " + sspath.path(6));
  71.     }
  72. }

其他BFS应用

BFS的重要性

树的广度优先遍历（层序遍历

图

  1. import java.util.ArrayList;
  2. import java.util.Collections;
  3. import java.util.LinkedList;
  4. import java.util.Queue;
  5.  
  6. // Unweighted Single Source Shortest Path
  7. public class USSSPath {
  8.  
  9.     private Graph G;
  10.     private int s;
  11.  
  12.     private boolean[] visited;
  13.     private int[] pre;
  14.     private int[] dis;
  15.  
  16.     public USSSPath(Graph G, int s){
  17.  
  18.         this.G = G;
  19.         this.s = s;
  20.  
  21.         visited = new boolean[G.V()];
  22.         pre = new int[G.V()];
  23.         dis = new int[G.V()];//给dis看空间
  24.         for(int i = 0; i < G.V(); i ++) {//给他俩所有值初始化
  25.             pre[i] = -1;
  26.             dis[i] = -1;
  27.         }
  28.         bfs(s);
  29.  
  30.         for(int i = 0; i < G.V(); i ++)//遍历所有点，打印所有点的dis值，不联通时值为-1
  31.             System.out.print(dis[i] + " ");
  32.         System.out.println();
  33.     }
  34.  
  35.     private void bfs(int s){
  36.  
  37.         Queue<Integer> queue = new LinkedList<>();
  38.         queue.add(s);
  39.         visited[s] = true;
  40.         pre[s] = s;
  41.         dis[s] = 0;//源点s到s的距离初始化为0
  42.         while(!queue.isEmpty()){
  43.             int v = queue.remove();
  44.  
  45.             for(int w: G.adj(v))
  46.                 if(!visited[w]){
  47.                     queue.add(w);
  48.                     visited[w] = true;
  49.                     pre[w] = v;
  50.                     dis[w] = dis[v] + 1;//距离为源点到v的距离+1
  51.                 }
  52.         }
  53.     }
  54.  
  55.     public boolean isConnectedTo(int t){
  56.         G.validateVertex(t);
  57.         return visited[t];
  58.     }
  59.  
  60.     public int dis(int t){//源点到目标t的最短路径长度
  61.         G.validateVertex(t);
  62.         return dis[t];
  63.     }
  64.  
  65.     public Iterable<Integer> path(int t){//源点到目标t的最短路径
  66.  
  67.         ArrayList<Integer> res = new ArrayList<Integer>();
  68.         if(!isConnectedTo(t)) return res;
  69.  
  70.         int cur = t;
  71.         while(cur != s){
  72.             res.add(cur);
  73.             cur = pre[cur];
  74.         }
  75.         res.add(s);
  76.  
  77.         Collections.reverse(res);
  78.         return res;
  79.     }
  80.  
  81.     public static void main(String[] args){
  82.  
  83.         Graph g = new Graph("g.txt");
  84.         USSSPath ussspath = new USSSPath(g, 0);
  85.         System.out.println("0 -> 6 : " + ussspath.path(6));
  86.         System.out.println("0 -> 6 : " + ussspath.dis(6));
  87.     }
  88. }

带权图和最小生成树

带权图

输入

  1. 7 12
  2. 0 1 2
  3. 0 3 7
  4. 0 5 2
  5. 1 2 1
  6. 1 3 4
  7. 1 4 3
  8. 1 5 5
  9. 2 4 4
  10. 2 5 4
  11. 3 4 1
  12. 3 6 5
  13. 4 6 7

代码

  1. import java.io.File;
  2. import java.io.IOException;
  3. import java.util.Map;
  4. import java.util.TreeMap;
  5. import java.util.Scanner;
  6.  
  7.  
  8. /// 暂时只支持无向带权图
  9. public class WeightedGraph implements Cloneable{
  10.  
  11.     private int V;
  12.     private int E;
  13.     private TreeMap<Integer, Integer>[] adj;//TreeMap比TreeSet多存一个值，可以当权，<顶点,权值类型>
  14.     public WeightedGraph(String filename){
  15.  
  16.         File file = new File(filename);
  17.  
  18.         try(Scanner scanner = new Scanner(file)){
  19.  
  20.             V = scanner.nextInt();//读取顶点数
  21.             if(V < 0) throw new IllegalArgumentException("V must be non-negative");
  22.             adj = new TreeMap[V];//定义一个数组
  23.             for(int i = 0; i < V; i ++)//为每个TreeMap开空间
  24.                 adj[i] = new TreeMap<Integer, Integer>();
  25.  
  26.             E = scanner.nextInt();
  27.             if(E < 0) throw new IllegalArgumentException("E must be non-negative");
  28.  
  29.             for(int i = 0; i < E; i ++){
  30.                 int a = scanner.nextInt();
  31.                 validateVertex(a);
  32.                 int b = scanner.nextInt();
  33.                 validateVertex(b);
  34.                 int weight = scanner.nextInt();//读取权值
  35.  
  36.                 if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");
  37.                 if(adj[a].containsKey(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");
  38.                 //adj的TreeMap里不包含以b元素为键的数据对，带权图处理平行边挺常见的，如果两个点直接有多条边，保留最短边
  39.  
  40.                 adj[a].put(b, weight);//从a-b之间有一条边，权值为weight
  41.                 adj[b].put(a, weight);
  42.             }
  43.         }
  44.         catch(IOException e){
  45.             e.printStackTrace();
  46.         }
  47.     }
  48.  
  49.     public void validateVertex(int v){
  50.         if(v < 0 || v >= V)
  51.             throw new IllegalArgumentException("vertex " + v + "is invalid");
  52.     }
  53.  
  54.     public int V(){
  55.         return V;
  56.     }
  57.  
  58.     public int E(){
  59.         return E;
  60.     }
  61.  
  62.     public boolean hasEdge(int v, int w){
  63.         validateVertex(v);
  64.         validateVertex(w);
  65.         return adj[v].containsKey(w);
  66.     }
  67.  
  68.     public Iterable<Integer> adj(int v){
  69.         validateVertex(v);
  70.         //不能直接返回TreeMap类的adj[v]，TreeMap中封装了一个keySet方法，可以返回所有的键对应的集合
  71.         return adj[v].keySet();
  72.     }
  73.  
  74.     public int getWeight(int v, int w){//获得v-w边所对应的权值
  75.  
  76.         if(hasEdge(v, w)) return adj[v].get(w);//有边抛权，无边抛异常
  77.         throw new IllegalArgumentException(String.format("No edge %d-%d", v, w));
  78.     }
  79.  
  80.     public int degree(int v){
  81.         validateVertex(v);
  82.         return adj[v].size();//返回v所对顶点对应的度
  83.     }
  84.  
  85.     //带权图基本不会有删边操作，把这个和clone移除基本不会影响
  86.     public void removeEdge(int v, int w){
  87.        validateVertex(v);
  88.         validateVertex(w);
  89.       if(adj[v].containsKey(w)) E --;
  90.           adj[v].remove(w);
  91.           adj[w].remove(v);
  92. }
  93.  
  94.     @Override
  95.     public Object clone(){
  96.  
  97.         try{
  98.             WeightedGraph cloned = (WeightedGraph) super.clone();
  99.             cloned.adj = new TreeMap[V];
  100.             for(int v = 0; v < V; v ++){
  101.                 cloned.adj[v] = new TreeMap<Integer, Integer>();//对每一个adj[v]开空间
  102.                 //遍历TreeMap，遍历它所有的键；Map接口下封装的Entry类，从adj[v]这个TreeMap中，
  103.                 // entrySet里面存的就是一个个键值数据对，把键和对应值放入entry中
  104.                 for(Map.Entry<Integer, Integer> entry: adj[v].entrySet())
  105.                 //adj[v]中put(键，值)
  106.                     cloned.adj[v].put(entry.getKey(), entry.getValue());
  107.             }
  108.             return cloned;
  109.         }
  110.         catch (CloneNotSupportedException e){
  111.             e.printStackTrace();
  112.         }
  113.         return null;
  114.     }
  115.  
  116.     @Override
  117.     public String toString(){
  118.         StringBuilder sb = new StringBuilder();
  119.  
  120.         sb.append(String.format("V = %d, E = %d\n", V, E));
  121.         for(int v = 0; v < V; v ++){
  122.             sb.append(String.format("%d : ", v));
  123.             for(Map.Entry<Integer, Integer> entry: adj[v].entrySet())//从adj[v].entrySet()中取出键值数据对
  124.                 sb.append(String.format("(%d: %d) ", entry.getKey(), entry.getValue()));
  125.             sb.append('\n');
  126.         }
  127.         return sb.toString();
  128.     }
  129.  
  130.     public static void main(String[] args){
  131.  
  132.         WeightedGraph g = new WeightedGraph("g.txt");
  133.         System.out.print(g);
  134.     }
  135. }

运行结果

最小生成树

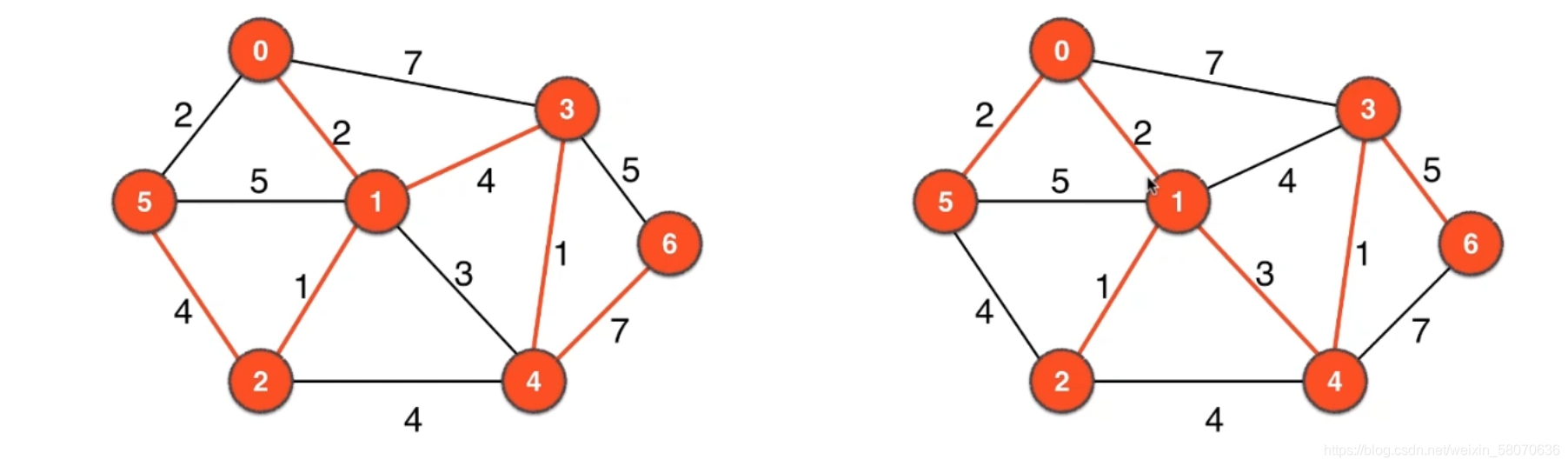
应用

从最小权值开始选边

用了4的这条边，就导致和其他小边构成了一个环

贪心算法难点在于，它为什么是对的

切分定理

横切边中的最短边，属于最小生成树

可以用用数学归纳法证明

Kruskal算法实现

  1. public class WeightedEdge implements Comparable<WeightedEdge>{
  2.  
  3.     private int v, w, weight;
  4.  
  5.     public WeightedEdge(int v, int w, int weight){
  6.         this.v = v;
  7.         this.w = w;
  8.         this.weight = weight;
  9.     }
  10.  
  11.     public int getV(){return v;}
  12.  
  13.     public int getW(){return w;}
  14.  
  15.     public int getWeight(){return weight;}
  16.  
  17.     @Override
  18.     public int compareTo(WeightedEdge another){
  19.         return weight - another.weight;
  20.     }
  21.  
  22.     @Override
  23.     public String toString(){
  24.         return String.format("(%d-%d: %d)", v, w, weight);
  25.     }
  26. }
  1. import java.util.ArrayList;
  2.  
  3. public class CC {//求带权图的联通分量个数
  4.  
  5.     private WeightedGraph G;
  6.     private int[] visited;
  7.     private int cccount = 0;
  8.  
  9.     public CC(WeightedGraph G){
  10.  
  11.         this.G = G;
  12.         visited = new int[G.V()];
  13.         for(int i = 0; i < visited.length; i ++)
  14.             visited[i] = -1;
  15.  
  16.         for(int v = 0; v < G.V(); v ++)
  17.             if(visited[v] == -1){
  18.                 dfs(v, cccount);
  19.                 cccount ++;
  20.             }
  21.     }
  22.  
  23.     private void dfs(int v, int ccid){
  24.  
  25.         visited[v] = ccid;
  26.         for(int w: G.adj(v))
  27.             if(visited[w] == -1)
  28.                 dfs(w, ccid);
  29.     }
  30.  
  31.     public int count(){
  32.         return cccount;
  33.     }
  34.  
  35.     public boolean isConnected(int v, int w){
  36.         G.validateVertex(v);
  37.         G.validateVertex(w);
  38.         return visited[v] == visited[w];
  39.     }
  40.  
  41.     public ArrayList<Integer>[] components(){
  42.  
  43.         ArrayList<Integer>[] res = new ArrayList[cccount];
  44.         for(int i = 0; i < cccount; i ++)
  45.             res[i] = new ArrayList<Integer>();
  46.  
  47.         for(int v = 0; v < G.V(); v ++)
  48.             res[visited[v]].add(v);
  49.         return res;
  50.     }
  51.     
  52. }
  1. import java.util.ArrayList;
  2. import java.util.Collections;
  3.  
  4. public class Kruskal {
  5.  
  6.     private WeightedGraph G;
  7.     private ArrayList<WeightedEdge> mst;//最小生成树返回的是用ArrayList存储的一个个边
  8.  
  9.     public Kruskal(WeightedGraph G){//用户传来一个带权图G
  10.  
  11.         this.G = G;
  12.         mst = new ArrayList<>();//开空间
  13.  
  14.         CC cc = new CC(G);//带权图中联通分量个数
  15.         if(cc.count() > 1) return;//有断开区域，最小生成树是null
  16.  
  17.         //Kruskal
  18.  
  19.         ArrayList<WeightedEdge> edges = new ArrayList<>();//存储所有的边
  20.         for(int v = 0; v < G.V(); v ++)//把所有边放入edges中
  21.             for(int w: G.adj(v))
  22.                 if(v < w)//防止类似0-2，2-0重复遍历的问题
  23.                     edges.add(new WeightedEdge(v, w, G.getWeight(v, w)));
  24.  
  25.         Collections.sort(edges);//把边传进去排序，记得设定WeightedEdge为可比较的类
  26.  
  27.          //判断是否行成环
  28.         UF uf = new UF(G.V());//有几个顶点UF中就有多少元素
  29.         for(WeightedEdge edge: edges){
  30.             int v = edge.getV();
  31.             int w = edge.getW();
  32.             if(!uf.isConnected(v, w)){//v和w不在一个集合时才连成边
  33.                 mst.add(edge);
  34.                 uf.unionElements(v, w);
  35.             }
  36.         }
  37.     }
  38.  
  39.     public ArrayList<WeightedEdge> result(){
  40.         return mst;
  41.     }//返回最小生成树
  42.  
  43.     public static void main(String[] args){
  44.  
  45.         WeightedGraph g = new WeightedGraph("g.txt");
  46.         Kruskal kruskal = new Kruskal(g);
  47.         System.out.println(kruskal.result());
  48.     }
  49. }

其中，Kruskal算法中快速判断是否生成环

  1. public class UF{
  2.  
  3.     private int[] parent;
  4.  
  5.     public UF(int n){
  6.  
  7.         parent = new int[n];
  8.         for(int i = 0 ; i < n ; i ++)
  9.             parent[i] = i;
  10.     }
  11.  
  12.     public int find(int p){
  13.         if( p != parent[p] )
  14.             parent[p] = find( parent[p] );
  15.         return parent[p];
  16.     }
  17.  
  18.     public boolean isConnected(int p , int q){
  19.         return find(p) == find(q);
  20.     }
  21.  
  22.     public void unionElements(int p, int q){
  23.  
  24.         int pRoot = find(p);
  25.         int qRoot = find(q);
  26.  
  27.         if( pRoot == qRoot )
  28.             return;
  29.  
  30.         parent[pRoot] = qRoot;
  31.     }
  32. }

时间复杂度：O(ElogE)

Prim算法 

  1. import java.util.ArrayList;
  2.  
  3. public class Prim {
  4.  
  5.     private WeightedGraph G;
  6.     private ArrayList<WeightedEdge> mst;
  7.  
  8.     public Prim(WeightedGraph G){
  9.  
  10.         this.G = G;
  11.         mst = new ArrayList<>();
  12.  
  13.         CC cc = new CC(G);
  14.         if(cc.count() > 1) return;//判断联通图
  15.  
  16.         //Prim
  17.         boolean[] visited = new boolean[G.V()];//切分在初始时，只有一个点切了
  18.         visited[0] = true;
  19.         for(int i = 1; i < G.V(); i ++){//共切V-1次
  20.  
  21.             WeightedEdge minEdge = new WeightedEdge(-1, -1, Integer.MAX_VALUE);//声明一个最大权值，用来用后面的小权值覆盖它
  22.             for(int v = 0; v < G.V(); v ++)//每次切的时候扫描所有的边
  23.                 if(visited[v])//当一个边访问过了，再访问它所有的邻边
  24.                     for(int w: G.adj(v))
  25.                         if(!visited[w] && G.getWeight(v, w) < minEdge.getWeight())//如果没访问过，且权值小于minEdge
  26.                             minEdge = new WeightedEdge(v, w, G.getWeight(v, w));//更新一下minEdge这条边
  27.             mst.add(minEdge);
  28.             visited[minEdge.getV()] = true;
  29.             visited[minEdge.getW()] = true;
  30.         }
  31.     }
  32.  
  33.     public ArrayList<WeightedEdge> result(){
  34.         return mst;
  35.     }
  36.  
  37.     public static void main(String[] args){
  38.  
  39.         WeightedGraph g = new WeightedGraph("g.txt");
  40.         Prim prim = new Prim(g);
  41.         System.out.println(prim.result());
  42.     }
  43. }

输入

  1. 7 12
  2. 0 1 2
  3. 0 3 7
  4. 0 5 2
  5. 1 2 1
  6. 1 3 4
  7. 1 4 3
  8. 1 5 5
  9. 2 4 4
  10. 2 5 4
  11. 3 4 1
  12. 3 6 5
  13. 4 6 7

输出

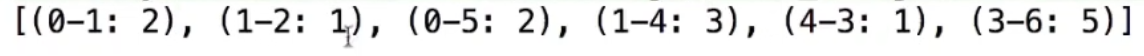
时间复杂度：O((V-1)*(V+E))=O(VE)

优先队列中所有的横切边不一定合法

这里的1-5，2-5，使用时先判断，非法的话直接扔掉就行

  1. import java.util.ArrayList;
  2. import java.util.Queue;
  3. import java.util.PriorityQueue;
  4.  
  5. public class Prim {
  6.  
  7.     private WeightedGraph G;
  8.     private ArrayList<WeightedEdge> mst;
  9.  
  10.     public Prim(WeightedGraph G){
  11.  
  12.         this.G = G;
  13.         mst = new ArrayList<>();
  14.  
  15.         CC cc = new CC(G);
  16.         if(cc.count() > 1) return;//判断联通图
  17.  
  18.         //Prim
  19.  
  20.         boolean visited[] = new boolean[G.V()];//切分在初始时，只有一个点切了
  21.         visited[0] = true;
  22.         Queue pq = new PriorityQueue<WeightedEdge>();//声明优先队列，里面存储带权边
  23.         for(int w: G.adj(0))//添加初始状态下的横切边，即所有和0相邻的边
  24.             pq.add(new WeightedEdge(0, w, G.getWeight(0, w)));
  25.  
  26.         while(!pq.isEmpty()){//如果用V-1个循环来弄的话还要判断是否合法
  27.  
  28.             WeightedEdge minEdge = (WeightedEdge) pq.remove();//这个minEdge有可能是最短横切边
  29.             if(visited[minEdge.getV()] && visited[minEdge.getW()])//如果minEdge两个端点都访问过，则非法，跳过它
  30.                 continue;
  31.  
  32.             mst.add(minEdge);//合法边加入mst最小生成树中
  33.  
  34.             //拓展切分，有可能产生新的最小横切边
  35.             int newv = visited[minEdge.getV()] ? minEdge.getW() : minEdge.getV();//判断哪个点没有被访问
  36.             visited[newv] = true;//没有访问的那个点设为已访问
  37.             for(int w: G.adj(newv))//取出newv的所有邻边
  38.                 if(!visited[w])
  39.                     //把有可能的最小横切边加入优先队列，在下一次的循环中从优先队列中取出最小的那个边
  40.                     pq.add(new WeightedEdge(newv, w, G.getWeight(newv, w)));
  41.         }
  42.     }
  43.  
  44.     public ArrayList<WeightedEdge> result(){
  45.         return mst;
  46.     }
  47.  
  48.     public static void main(String[] args){
  49.  
  50.         WeightedGraph g = new WeightedGraph("g.txt");
  51.         Prim prim = new Prim(g);
  52.         System.out.println(prim.result());
  53.     }
  54. }

时间复杂度:O(Elog E）首选（因为其他语言几乎没有并查集

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小小林熬夜学编程/article/detail/152134
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号