leetcode(96)不同的二叉搜索树——卡塔兰数_不同的二叉搜索数 卡特兰数

题目描述
给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:
输入: 3
输出: 5

解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

1
2
3
4
5
6
7
8
9

思路

方法一 动态规划
给定一个有序序列 1 … n，为了根据序列构建一棵二叉搜索树。我们可以遍历每个数字 i，将该数字作为树根，1 … (i-1) 序列将成为左子树，(i+1) … n 序列将成为右子树。于是，我们可以递归地从子序列构建子树。 在上述方法中，由于根各自不同，每棵二叉树都保证是独特的。

可见，问题可以分解成规模较小的子问题。因此，我们可以存储并复用子问题的解，而不是递归的（也重复的）解决这些子问题，这就是动态规划法。

算法

问题是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：

G(n): 长度为n的序列的不同二叉搜索树个数。

F(i, n): 以i为根的不同二叉搜索树个数( 1 ≤ i ≤ n)。

可见，

G(n) 是我们解决问题需要的函数。

G(n)可以从 F(i, n)得到，而 F(i, n) 又会递归的依赖于 G(n)G(n)。

首先，不同的二叉搜索树的总数 G(n)，是对遍历所有 i (1 <= i <= n) 的 F(i, n) 之和。换而言之：

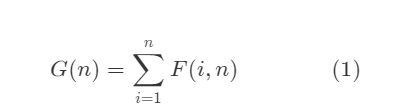
特别的，对于边界情况，当序列长度为 1 （只有根）或为 0 （空树）时，只有一种情况。亦即：

G(0)=1,G(1)=1

给定序列 1 … n，我们选出数字 i 作为根，则对于根 i 的不同二叉搜索树数量 F(i, n)，是左右子树个数的笛卡尔积，如下图所示:

举例而言，F(3, 7)，以 3 为根的不同二叉搜索树个数。为了以 3 为根从序列 [1, 2, 3, 4, 5, 6, 7] 构建二叉搜索树，我们需要从左子序列 [1, 2] 构建左子树，从右子序列 [4, 5, 6, 7] 构建右子树，然后将它们组合(即笛卡尔积)。 巧妙之处在于，我们可以将 [1,2] 构建不同左子树的数量表示为 G(2), 从 [4, 5, 6, 7]` 构建不同右子树的数量表示为 G(4)。这是由于 G(n) 和序列的内容无关，只和序列的长度有关。于是，F(3,7)=G(2)⋅G(4)。 概括而言，我们可以得到以下公式：

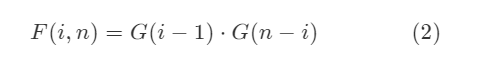
将公式 (1)，(2) 结合，可以得到 G(n)的递归表达公式：
为了计算函数结果，我们从小到大计算，因为 G(n) 的值依赖于 G(0)…G(n−1)。

根据以上的分析和公式，很容易实现计算G(n) 的算法。 下面是示例:

public class Solution {
  public int numTrees(int n) {
    int G[n+1];
    G[0] = 1;
    G[1] = 1;

    for (int i = 2; i <= n; ++i) {
      for (int j = 1; j <= i; ++j) {
        G[i] += G[j - 1] * G[i - j];
      }
    }
    return G[n];
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

时间复杂度为 O(N^2)

**方法二 卡塔兰数 **

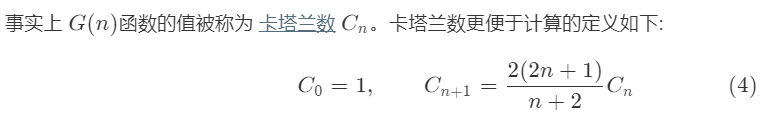
class Solution {
public:
    int numTrees(int n) {
         // Note: we should use long here instead of int, otherwise overflow
    long C = 1;
    for (int i = 0; i < n; ++i) {
      C = C * 2 * (2 * i + 1) / (i + 2);
    }
    return (int) C;
    }
};
1
2
3
4
5
6
7
8
9
10
11

卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。

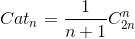
Catalan数相关的算法问题