ddpm代码注释_def p_mean_variance(self, x, t, clip_denoised: boo

import math
import torch
from torch import nn, einsum
import torch.nn.functional as F
from inspect import isfunction
from functools import partial
import numpy as np
from tqdm import tqdm
# 注释的参数文章: Understanding Diffusion Models: A Unified Perspective

def _warmup_beta(linear_start, linear_end, n_timestep, warmup_frac):
    betas = linear_end * np.ones(n_timestep, dtype=np.float64)
    warmup_time = int(n_timestep * warmup_frac)
    betas[:warmup_time] = np.linspace(
        linear_start, linear_end, warmup_time, dtype=np.float64)
    return betas


def make_beta_schedule(schedule, n_timestep, linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):
    if schedule == 'quad':
        betas = np.linspace(linear_start ** 0.5, linear_end ** 0.5,
                            n_timestep, dtype=np.float64) ** 2
    elif schedule == 'linear':
        betas = np.linspace(linear_start, linear_end,
                            n_timestep, dtype=np.float64)
    elif schedule == 'warmup10':
        betas = _warmup_beta(linear_start, linear_end,
                             n_timestep, 0.1)
    elif schedule == 'warmup50':
        betas = _warmup_beta(linear_start, linear_end,
                             n_timestep, 0.5)
    elif schedule == 'const':
        betas = linear_end * np.ones(n_timestep, dtype=np.float64)
    elif schedule == 'jsd':  # 1/T, 1/(T-1), 1/(T-2), ..., 1
        betas = 1. / np.linspace(n_timestep,
                                 1, n_timestep, dtype=np.float64)
    elif schedule == "cosine":
        timesteps = (
            torch.arange(n_timestep + 1, dtype=torch.float64) /
            n_timestep + cosine_s
        )
        alphas = timesteps / (1 + cosine_s) * math.pi / 2
        alphas = torch.cos(alphas).pow(2)
        alphas = alphas / alphas[0]
        betas = 1 - alphas[1:] / alphas[:-1]
        betas = betas.clamp(max=0.999)
    else:
        raise NotImplementedError(schedule)
    return betas


# gaussian diffusion trainer class

def exists(x):
    return x is not None


def default(val, d):
    if exists(val):
        return val
    return d() if isfunction(d) else d

# 提取t_step的系数
def extract(a, t, x_shape):
    b, *_ = t.shape
    out = a.gather(-1, t)
    return out.reshape(b, *((1,) * (len(x_shape) - 1)))


def noise_like(shape, device, repeat=False):
    def repeat_noise(): return torch.randn(
        (1, *shape[1:]), device=device).repeat(shape[0], *((1,) * (len(shape) - 1)))

    def noise(): return torch.randn(shape, device=device)
    return repeat_noise() if repeat else noise()


class GaussianDiffusion(nn.Module):
    def __init__(
        self,
        denoise_fn,
        image_size,
        channels=3,
        loss_type='l1',
        conditional=True,
        schedule_opt=None
    ):
        super().__init__()
        # 设置去噪网络和损失函数
        self.channels = channels
        self.image_size = image_size
        self.denoise_fn = denoise_fn
        self.conditional = conditional
        self.loss_type = loss_type
        if schedule_opt is not None:
            pass
            # self.set_new_noise_schedule(schedule_opt)

    def set_loss(self, device):
        if self.loss_type == 'l1':
            self.loss_func = nn.L1Loss(reduction='sum').to(device)
        elif self.loss_type == 'l2':
            self.loss_func = nn.MSELoss(reduction='sum').to(device)
        else:
            raise NotImplementedError()

    def set_new_noise_schedule(self, schedule_opt, device):
        to_torch = partial(torch.tensor, dtype=torch.float32, device=device)
        # 生成betas 参数
        betas = make_beta_schedule(
            schedule=schedule_opt['schedule'],
            n_timestep=schedule_opt['n_timestep'],
            linear_start=schedule_opt['linear_start'],
            linear_end=schedule_opt['linear_end'])
        betas = betas.detach().cpu().numpy() if isinstance(betas, torch.Tensor) else betas
        alphas = 1. - betas
        alphas_cumprod = np.cumprod(alphas, axis=0)# 累乘
        alphas_cumprod_prev = np.append(1., alphas_cumprod[:-1])

        timesteps, = betas.shape
        self.num_timesteps = int(timesteps)
        self.register_buffer('betas', to_torch(betas))
        self.register_buffer('alphas_cumprod', to_torch(alphas_cumprod))
        self.register_buffer('alphas_cumprod_prev',
                             to_torch(alphas_cumprod_prev))

        # calculations for diffusion q(x_t | x_{t-1}) and others
        self.register_buffer('sqrt_alphas_cumprod',
                             to_torch(np.sqrt(alphas_cumprod)))
        self.register_buffer('sqrt_one_minus_alphas_cumprod',
                             to_torch(np.sqrt(1. - alphas_cumprod)))
        self.register_buffer('log_one_minus_alphas_cumprod',
                             to_torch(np.log(1. - alphas_cumprod)))
        self.register_buffer('sqrt_recip_alphas_cumprod',
                             to_torch(np.sqrt(1. / alphas_cumprod)))
        self.register_buffer('sqrt_recipm1_alphas_cumprod',
                             to_torch(np.sqrt(1. / alphas_cumprod - 1)))

        # calculations for posterior q(x_{t-1} | x_t, x_0)
        posterior_variance = betas * \
            (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
        # above: equal to 1. / (1. / (1. - alpha_cumprod_tm1) + alpha_t / beta_t)
        self.register_buffer('posterior_variance',
                             to_torch(posterior_variance))
        # below: log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
        self.register_buffer('posterior_log_variance_clipped', to_torch(
            np.log(np.maximum(posterior_variance, 1e-20))))
        self.register_buffer('posterior_mean_coef1', to_torch(
            betas * np.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod)))
        self.register_buffer('posterior_mean_coef2', to_torch(
            (1. - alphas_cumprod_prev) * np.sqrt(alphas) / (1. - alphas_cumprod)))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152

正向扩散链的过程，返回分布的均值与方差，见公式61

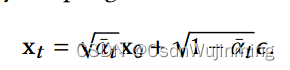
# 由q(xt|x_t-1)推导出的q(xt|x_0)的分布，获取第t步扩散分布的：均值，方差，由迭代推导出的关系，见公式61
    def q_mean_variance(self, x_start, t):
        mean = extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
        variance = extract(1. - self.alphas_cumprod, t, x_start.shape)
        log_variance = extract(
            self.log_one_minus_alphas_cumprod, t, x_start.shape)
        return mean, variance, log_variance
1
2
3
4
5
6
7

predict_start_from_noise方法从噪声中预测原始图像，对应公式115

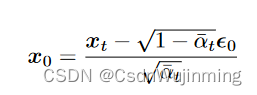
# 逆扩散运算， 由迭代推出的关系： f(x_0)=x_t, 通过f^-1，计算出x_0，用于计算噪声估计的误差，见公式69，115
    def predict_start_from_noise(self, x_t, t, noise):
        return (
            extract(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
            extract(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
        )
1
2
3
4
5
6

返回q_posterior ：q(x_t-1|xt, x0)的均值和方差，公式71

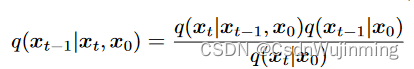
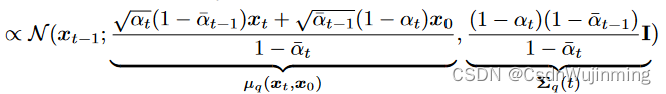
# 计算q(x_t-1|xt, x0)的分布， 这个可以用q(x_t|xt-1, x0)=q(x_t|xt-1)与q(x_t-1|x0)表示，下面就是推导结果的计算，见公式71
    def q_posterior(self, x_start, x_t, t):
        posterior_mean = (
        # extract(self.posterior_mean_coef1, t, x_t.shape) 为上面均值部分x_t的系数
            extract(self.posterior_mean_coef1, t, x_t.shape) * x_start +
            extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
        )
        posterior_variance = extract(self.posterior_variance, t, x_t.shape)
        posterior_log_variance_clipped = extract(
            self.posterior_log_variance_clipped, t, x_t.shape)
        return posterior_mean, posterior_variance, posterior_log_variance_clipped
1
2
3
4
5
6
7
8
9
10
11

公式94

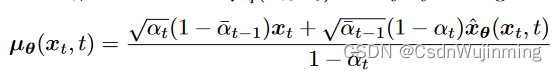
# 计算神经网络重构的原始图片下的去噪分布p(x_t-1|x_t)
    def p_mean_variance(self, x, t, clip_denoised: bool, condition_x=None):
        if condition_x is not None:
            # 从神经网络预测的噪声中重构出样本，即网络预测的x_0
            x_recon = self.predict_start_from_noise(
                x, t=t, noise=self.denoise_fn(torch.cat([condition_x, x], dim=1), t))# 送入模型，得到t时刻的随机噪声预测值
        else:
            x_recon = self.predict_start_from_noise(
                x, t=t, noise=self.denoise_fn(x, t))

        if clip_denoised:
            x_recon.clamp_(-1., 1.)
        # 计算q(x_t-1|xt, x_recon)的分布参数，见公式94
        model_mean, posterior_variance, posterior_log_variance = self.q_posterior(
            x_start=x_recon, x_t=x, t=t)
        return model_mean, posterior_variance, posterior_log_variance
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

正向扩散一次

# 用模型逆扩散一次
    @torch.no_grad()# 表示不参与反射传播
    def p_sample(self, x, t, clip_denoised=True, repeat_noise=False, condition_x=None):
        b, *_, device = *x.shape, x.device
        model_mean, _, model_log_variance = self.p_mean_variance(
            x=x, t=t, clip_denoised=clip_denoised, condition_x=condition_x)
        noise = noise_like(x.shape, device, repeat_noise)
        # no noise when t == 0
        nonzero_mask = (1 - (t == 0).float()).reshape(b,
                                                      *((1,) * (len(x.shape) - 1)))
        return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise
1
2
3
4
5
6
7
8
9
10
11

# 基于扩散参数采样，见公式61-70
    def q_sample(self, x_start, t, noise=None):
        noise = default(noise, lambda: torch.randn_like(x_start))

        # fix gama
        return (
            extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
            extract(self.sqrt_one_minus_alphas_cumprod,
                    t, x_start.shape) * noise
        )
1
2
3
4
5
6
7
8
9
10

计算噪声预测的误差

def p_losses(self, x_in, noise=None):
        x_start = x_in['RES']
        [b, c, h, w] = x_start.shape
        # 对一个batch 生成随机的时刻t
        t = torch.randint(0, self.num_timesteps, (b,),
                          device=x_start.device).long()
        # 生成一个随机的噪声
        noise = default(noise, lambda: torch.randn_like(x_start))
        # 加上噪声后，t 次扩散的样本
        x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise)
        # 送入模型，得到t时刻的随机噪声预测值
        if not self.conditional:
            # 这个x_recon实际是去噪网络估计的噪声，网络可以直接重构图片，但这里是估计的噪声，这样设置可以年ddpm论文
            x_recon = self.denoise_fn(
                torch.cat([x_in['P'], x_in['SR'], x_noisy], dim=1), t)
        else:
            x_recon = self.denoise_fn(
                torch.cat([x_in['P'], x_in['SR'], x_noisy], dim=1), t)
        # 与真实噪声一起计算误差
        loss = self.loss_func(noise, x_recon)

        return loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22