pytorch中关于BF16、FP16的一些操作

前提

好久没更新博客了，最近在学习过程中遇到了如何生成一个float16的数或者生成一个bfloat16的数，并对其二进制的存储格式进行一些操作的问题，这里做一个简单的记录。

创建BF16和FP16的数据

经过查阅资料发现，python的numpy库可以创建一个FP16的数，但是无法创建BF16的数。pytorch的话，可以创建数据类型为FP16，也可以创建数据类型为BF16的数。所以我们使用pytorch来创建这两种数据格式。

import torch
torch.set_printoptions(precision=32) # print的显示位数

A = torch.rand(1, dtype=torch.bfloat16)
B = torch.rand(1, dtype=torch.float16)

print(f"A: {A}") # A: tensor([0.07031250000000000000000000000000], dtype=torch.bfloat16)
print(f"B: {B}")  # B: tensor([0.03320312500000000000000000000000], dtype=torch.float16)
1
2
3
4
5
6
7
8

BF16和FP16的二进制存储格式

参考FP32，TF32，FP16，BF16介绍这篇文章可知。类型为BF16的数据有16bit，1bit为符号位，8bit为指数位，7bit为尾数位；类型为FP16的数据也有16bit，1bit为符号位，5bit为指数位，10bit为尾数位。
同一个十进制数，例如0.75，在数据类型分别为BF16和FP16的情况下，对应的二进制存储肯定是不相同的。那么如何得到BF16和FP16十进制数对应的二进制存储呢？

如何根据十进制数得到对应的二进制存储

代码如下：

import torch
torch.set_printoptions(precision=32)

A = torch.tensor(0.785, dtype=torch.bfloat16)
B = torch.tensor(0.785, dtype=torch.float16)
print(f"A: {A}")   # A: 0.78515625
print(f"B: {B}")   # B: 0.78515625

int16_A = A.view(torch.int16)
int16_B = B.view(torch.int16)


print(bin(int16_A))  # 0b11111101001001
print(bin(int16_B))  # 0b11101001001000
1
2
3
4
5
6
7
8
9
10
11
12
13
14

首先说明，虽然我们创建tensor时输入的数据为0.785，但是实际数据是0.78515625，这里不做多余解释，只当我们创建的tensor大小为0.78515625。
先对int16_A = A.view(torch.int16)这行代码做个解析，如果我们直接使用bin(A)代码是会报错的，报错信息是：only integer tensors of a single element can be converted to an index。这是因为只有整型tensor才可以使用bin，我们使用view函数将类型位BF16的数据A所拥有的16个bit位看作是一个int16的整数，FP16同理。如下图所示。

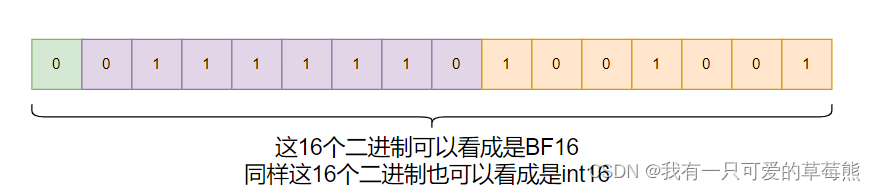
这样的话我们就可以使用bin查看其二进制存储。在这里我们多说一句：负数在计算机中以补码存储，而正数以原码存储。而符号位0/1代表了这个数是整数还是负数，稍后我们会使用bin查看一个负数得出的二进制存储。

接下来我们对bin(int16_A)的结果进行说明。我们可以看到结果是0b11111101001001，其中0b代表了这个数是二进制，除过0b外，剩下14bit的0/1，那这不对呀，BF16要有16bit的二进制呢。原因在于，bin输出的结果会将前面多余的0省略，我们补上两个0就是16bit了。FP16同理。

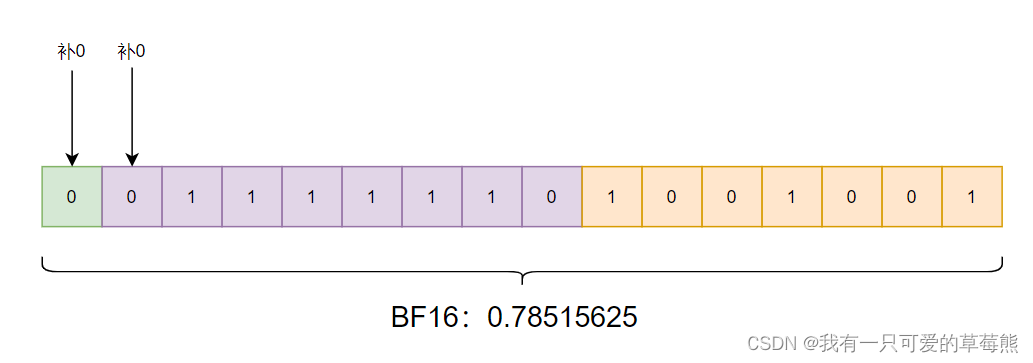
所以0011111101001001就是BF16(0.78515625)所对应的二进制存储。

如何根据二进制存储计算对应的十进制数？

这里我们还是使用上面的0.78515625进行解释。符号位为：0，指数位位：01111110，尾数位为：1001001。

第一种方法

$$(-1{)}^{\text{sign}}\times 2^{\text{exp}-127}\times (2^0+\text{frac}{)}_2$$
frac代表尾数，exp代表指数，sign代表符号，127是bias(偏置，FP16的中bias为15)，1.0代表了隐藏数(隐藏位)。将指数01111110变为十进制的数为126。这个公式中的乘法以及frac都是二进制的。如果这里你不太明白，下面还有一种十进制的方法，你可以进行对比。

将公式套用进去得到
$$(-1{)}^0\times (1.0+0.1001001)\times 2^{126-127}=1\times 1.1001001\times 2^{-1}$$

$1.1001001\times 2^{-1}$ 的意思是将小数点向左移动一位，2的指数是负几，就向左移动几位。如果是正数的话，就向右移动。因此我们得到0.11001001，这是一个二进制数，我们现在要将他转为整数。如下：
$$2^{-1}+2^{-2}+2^{-5}+2^{-8}=0.78515625$$
如果这里不明白如何将二进制数转为十进制数，可以自行百度。

第二种方法

公式如下：
$$(-1{)}^{\text{sign}}\times 2^{\text{exp}-127}\times (2^0+\text{frac}{)}_{10}$$

乍一看，这个公式和上面的没有区别。是的，的确没有区别，只不过这里我们计算frac时是十进制的。
我们先将frac转为十进制，也就是将0.1001001转为十进制，计算如下：
$$2^{-1}+2^{-4}+2^{-7}=0.5703125$$
然后将其带入公式中如下：
$$(-1{)}^0\times (2^0+0.5703125)\times 2^{126-127}=1\times 1.5703125\times 2^{-1}=0.78515625$$

可以看到两种计算方式的结果是一样的。第一种方式是使用二进制进行运算，最后将结果转为十进制；第二种方式是直接使用十进制进行计算，结果就直接是十进制的。

二进制乘法

有两个二进制，比如说一个是11011，另一个是01001，那么两个二进制做乘法的结果是多少呢？这里当时犯了一个比较愚蠢的错误，二进制的乘法的结果就是其对应十进制的乘法再转为二进制结果。
11011对应的十进制数是27，01001对应的十进制数是9，所以如下：
$$(11011{)}_2\times (01001{)}_2=((27{)}_{10}\times (9{)}_{10}{)}_2=11110011$$
我们手算一下看结果是否正确。

可以看到结果完全正确，二进制的乘法就是遇2进一。

如果是负数怎么办？

相同的代码，只不过我们这里是负数，然后使用bin来得到其二进制存储。

import torch
torch.set_printoptions(precision=32)

A = torch.tensor(-0.785, dtype=torch.bfloat16)
print(f"A: {A}")   # A: -0.78515625


int16_A = A.view(torch.int16)
print(int16_A)
print(bin(int16_A))  # -0b100000010110111
1
2
3
4
5
6
7
8
9
10

在解释这段代码及结果之前，我们先看看windows自带的计算其中，一个负数对应的二进制为多少。

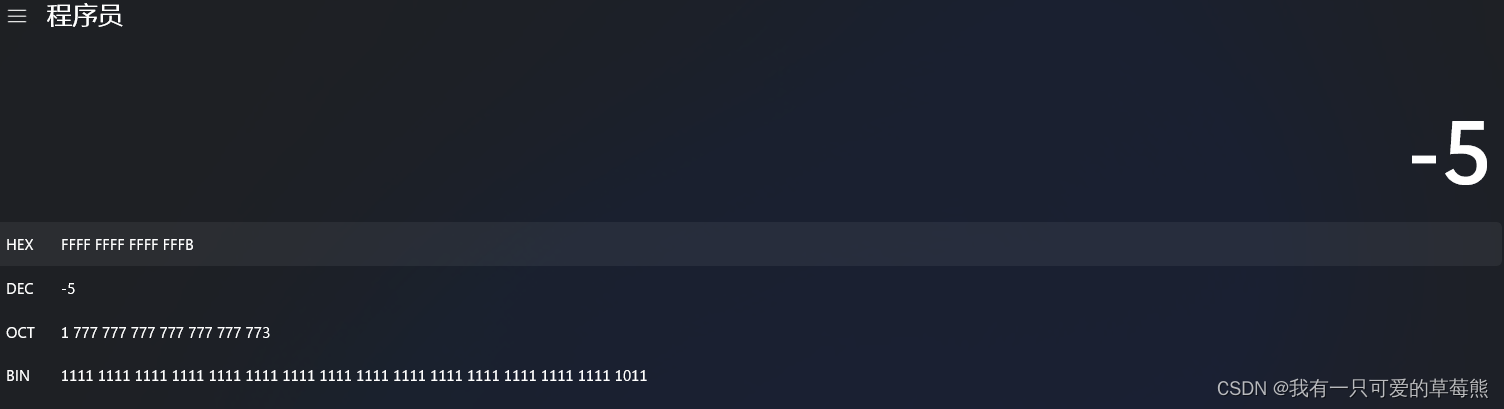
那么5呢，5是多少？

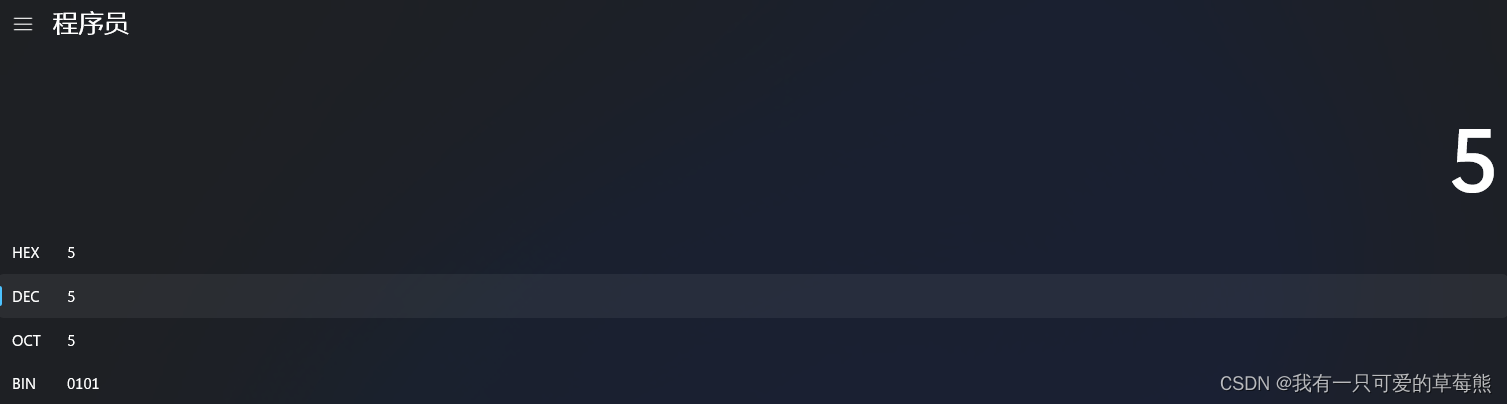
可以看到，并不是我们说的负数和正数只不过符号位一个是1，一个是0而已。这句话至关重要：负数在计算机中以补码存储，而正数以原码存储。

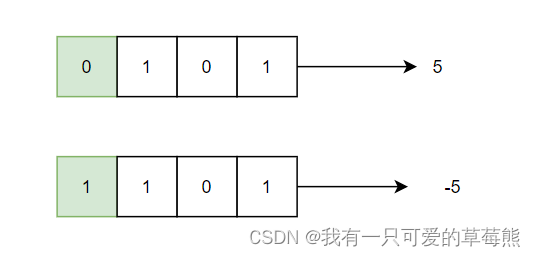
按理来说，这样才是正确的，其中绿色的框代表了符号位。但是负数在计算机中是按照补码存储的，求补码的方式就是反码+1，如下图所示：

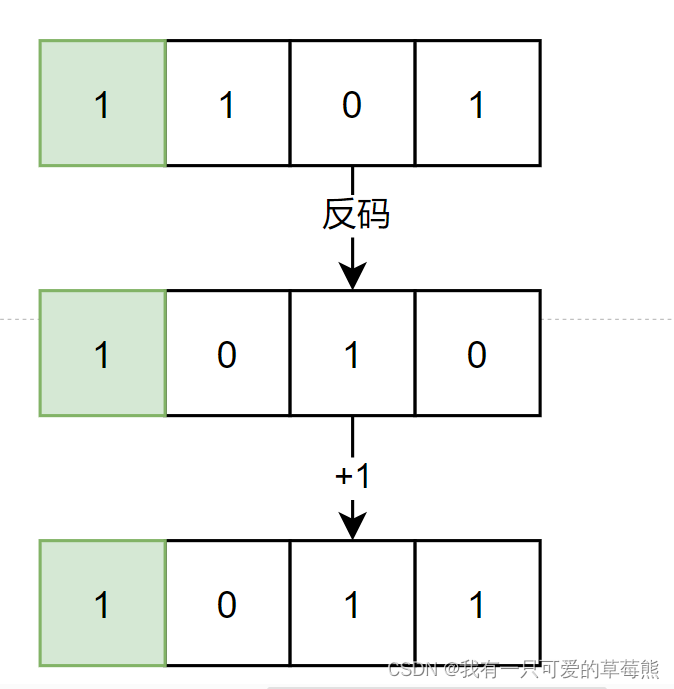
这下应该可以明白为什么计算器得出的结果不是我们想要的了。因为它输出的是-5的补码，同理当我们对一个负数使用bin()函数时，输出的也是它的补码。

我们将这个结论应用大到BF16的负数中，看是否成立。

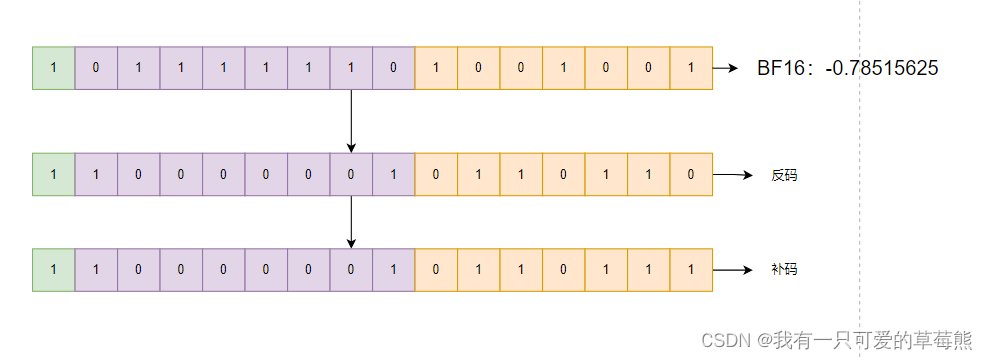
bin输出的结果是-0b100000010110111，这个-符号就代表了这个数是负数，我们将它转为1即可，同时如果有空缺的bit位置补0即可，所以bin输出的结果就是：1100000010110111，可以看到和我们手动推导的一样。

这里要指出，如果你使用bin(-5)的话，会得到一个-0b101的结果，和我们上面解释的并不一样，这里博主也不太清楚原因，如有了解的，欢迎告知。

如何手动计算BF16对应的的二进制存储格式

上面我们是编程得到BF16的二进制存储格式，那么如何手算呢？这里给出方法。如何计算BF16类型的数据0.78515625对应的二进制存储格式。

1. 将0.78515625分为整数和小数两部分求二进制
   $$0.78515325=0.11001001$$
2. 移动小数点，使其位于第一个非0位和其后一位中间。
   $$0.11001001=1.1001001\times 2^{-1}$$
3. 计算指数和尾数
   $$\begin{gathered} exp=-1+127=126=(1111110{)}_2 \\ frac=(1001001{)}_2 \end{gathered}$$
4. 将符号位，指数位，尾数位拼起来，注意指数位要补0
   $$(0.78515325{)}_{10}=[0][01111110][1001001]$$

参考链接

1. https://blog.csdn.net/qq_41298763/article/details/135705243
2. https://www.jianshu.com/p/7affd951b3e4