决策树C4.5算法详解_c4.5决策树算法

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/zjsghww/article/details/51638126

首先，C4.5是决策树算法的一种。决策树算法作为一种分类算法，目标就是将具有p维特征的n个样本分到c个类别中去。相当于做一个投影，c=f(n)，将样本经过一种变换赋予一种类别标签。决策树为了达到这一目的，可以把分类的过程表示成一棵树，每次通过选择一个特征pi来进行分叉。

那么怎样选择分叉的特征呢？每一次分叉选择哪个特征对样本进行划分可以最快最准确的对样本分类呢？不同的决策树算法有着不同的特征选择方案。ID3用信息增益，C4.5用信息增益率，CART用gini系数。

下面主要针对C4.5算法，我们用一个例子来计算一下。

                                                                                                                                                    

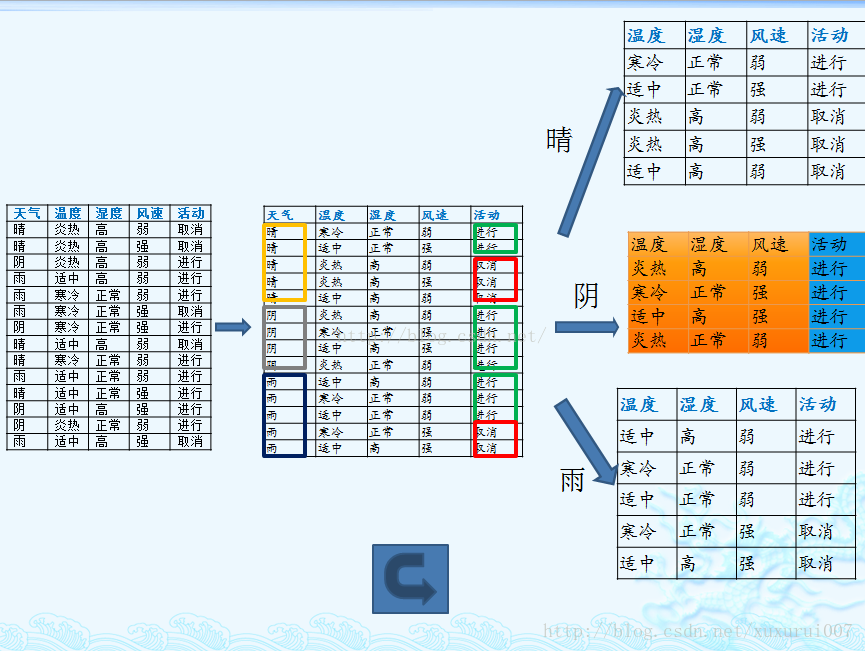
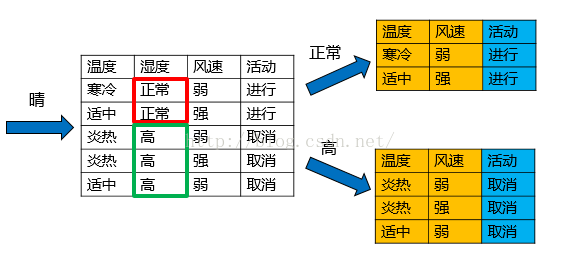
上述数据集有四个属性，属性集合A={ 天气，温度，湿度，风速}， 类别标签有两个，类别集合L={进行，取消}。

 

1. 计算类别信息熵

类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念，熵越大，不确定性就越大，把事情搞清楚所需要的信息量就越多。

 

 

2. 计算每种划分方式的条件熵
它表示的是在某种属性的条件下，各种类别出现的不确定性之和。条件熵，表示这个属性中拥有的样本类别越不“纯”。

 

3. 计算信息增益

信息增益的 = 熵 - 条件熵，在这里就是 类别信息熵 - 每种划分方式的条件熵，它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大，就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性，当然，选择该属性就可以更快更好地完成我们的分类目标。

信息增益就是ID3算法的特征选择指标。

 

 

信息增益的直观意义是标签被属性划分后的不确定性的减少量，如果单纯的以信息增益作为判断标准，可想而知，当某个属性的取值有很多时，标签会被划分成很多份，于是其不确定性自然会减少很多，这时候ID3算法就会更倾向于选择这个属性作为划分依据了，这显然不是我们想要的。所以，C4.5选择使用信息增益率对ID3进行改进。

 

4.计算属性分裂信息度量（属性熵）

用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息，我们把这些信息称为属性的内在信息（instrisic information）。信息增益率用信息增益 / 内在信息，会导致属性的重要性随着内在信息的增大而减小（也就是说，如果这个属性本身不确定性就很大，那我就越不倾向于选取它），这样算是对单纯用信息增益有所补偿。

 

 

5. 计算信息增益率

（下面写错了。。应该是IGR = Gain / H ）

 

天气的信息增益率最高，选择天气为分裂属性。发现分裂了之后，天气是“阴”的条件下，类别是”纯“的，所以把它定义为叶子节点，选择不“纯”的结点继续分裂。

 

                                                     

                                                    

                                  

在子结点当中重复过程1~5。

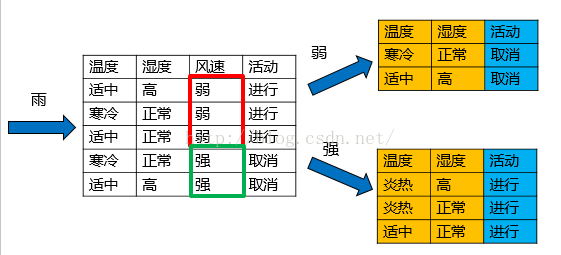
以天气=“雨”的子结点为例：

1. 计算类别信息熵

2. 计算每个属性的信息熵

3. 计算信息增益

4.计算属性分裂信息度量

5. 计算信息增益率

（下面写错了。。应该是IGR = Gain / H ）

风速属性的信息增益率最高，所以选择风速作为分裂结点，分裂之后，发现子结点都是纯的，因此子节点均为叶子节点，分裂结束。

至此，这个数据集上C4.5的计算过程就算完成了，一棵树也构建出来了。

 

现在我们来总结一下C4.5的算法流程：