经典损失函数——均方误差(MSE)和交叉熵误差(CEE)的python实现_python mse函数

损失函数（loss function）用来表示当前的神经网络对训练数据不拟合的程度。这个损失函数有很多，但是一般使用均方误差和交叉熵误差等。

1.均方误差（mean squared error）

先来看一下表达式：

                           $E=\frac{1}{2}\sum_{k}^{ }(y_{k}-t_{k})^{2}$

$\frac{1}{2}$用于将$\frac{1}{2}\sum_{k}^{ }(y_{k}-t_{k})^{2}$的求导结果变成$\sum_{k}^{ }(y_{k}-t_{k})$，$y_{k}$是神经网络的输出，$t_{k}$是训练数据的标签值，k表示数据的维度。

用python实现：

def MSE(y, t):
    return 0.5 * np.sum((y - t)**2)

使用这个函数来具体计算以下：

t = [0, 1, 0, 0]
y = [0.1, 0.05, 0.05, 0.8]
print(MSE(np.array(y), np.array(t)))
 
 
t = [0, 1, 0, 0]
y = [0.1, 0.8, 0.05, 0.05]
print(MSE(np.array(y), np.array(t)))

输出结果为：

                                                  

这里正确标签用one-hot编码，y用softmax输出表示。第一个例子的正确标签为2，对应的概率为0.05，第二个例子对应标签为0.8.可以发现第二个例子的损失函数的值更小，和训练数据更吻合。

2.交叉熵误差（cross entropy error）

除了均方误差之外，交叉熵误差也常被用做损失函数。表达式为：

          $E=-\sum_{k}^{ }(t_{k}\textrm{log}y_{k})$

这里，log表示以e为底的自然对数（$\mathrm{log}_{e}$)。$y_{k}$是神经网络的输出，$t_{k}$是训练数据的标签值。并且，$t_{k}$中只有正确解标签的索引为1，其他均为0（one-hot）表示。因此这个式子实际上只计算对应正确解标签的输出的自然对数。

自然对数的图像为：

                                                

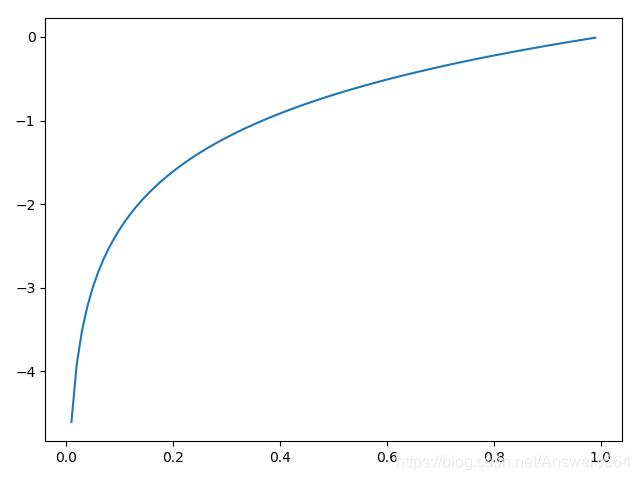
所以输出的概率越大对应损失函数的值越低。

代码实现交叉熵误差：

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

这里设置delta，是因为当出现log(0)时，np.log(0)会变为负无穷大。所以添加一个微小值可以防止负无穷大的发生。

还用刚刚那个例子：

t = [0, 1, 0, 0]
y = [0.1, 0.05, 0.05, 0.8]
print(cross_entropy_error(np.array(y), np.array(t)))
 
 
t = [0, 1, 0, 0]
y = [0.1, 0.8, 0.05, 0.05]
print(cross_entropy_error(np.array(y), np.array(t)))

输出为：

                                                   

可以看出输出值的概率越大损失值就越小。

 

• 交叉熵误差的改进：

前面介绍了损失函数的实现都是针对单个数据。如果要求所有训练数据的损失函数的总和，以交叉熵为例，可以写成下面的式子：

                                            $E=-\frac{1}{N}\sum_{n}^{ }\sum_{k}^{ }(t_{nk}\textrm{log}y_{nk})$

这里，假设数据有N个，$t_{nk}$表示第n个数据的第k个元素的值。式子虽然看起来复杂，其实只是把求单个数据的损失函数扩大到了N份数据，不过最后要除以N进行正规化。

通过除以N，可以求单个数据的“平均损失函数”。通过这样的平均化，可以获得和训练数据的数量无关的统一指标。比如，即使训练数据有100或1000个，也可以求得单个数据的平均损失函数。

所以对之前计算单个数据交叉熵进行改进,可以同时处理单个数据和批量数据:

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
 
    batch_size = y.shape[0]
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / batch_size

但是，对于训练数据不是one-hot表示，而是普通标签表示怎么办呢（例如一批处理5个数据的标签值为[2,5,7,3,4]）。输出的数组是5行N列的，这里以手写数字识别为例所以N=10。所以我们计算的交叉熵误差其实计算的是对应每一行，其中某一列的对数之和。例如标签值[2,5,7,3,4]，选择的是输出结果的第一行第2个，第二行第5个，第三行第7个...可能表达的不是很清楚，看下代码实现应该好多了。

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
 
    batch_size = y.shape[0]
    delta = 1e-7
    return -np.sum(np.log(y[np.arange(batch_size), t] + delta)) / batch_size

也就是说，这里的标签值是作为输出数组的索引，用于定位。