(Leiden)From Louvain to Leiden:guaranteeing well-connected communities_leiden算法

Leiden算法

论文地址
Leiden算法是近几年的SOTA算法之一。

Louvain 算法有一个主要的缺陷：可能会产生任意的连接性不好的社区(甚至不连通)。为了解决这个问题，作者引入了Leiden算法。证明了该算法产生的社区保证是连通的。此外证明了当Leiden算法迭代应用时，它收敛于一个划分，其中所有社区的所有子集都是局部最优分配的。并且算法速度比Louvain算法更快。

通常社区划分的网络结构是未知的，所以我们选择模块度来评价社区发现结果。

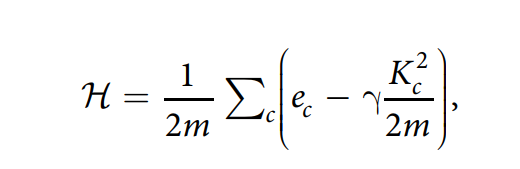
m总边数 ec社区c内的边数 kc社区c节点的度和

其中γ>0是分辨率参数。更高的导致更多的社区，而更低的导致更少的社区。

对于模块度优化，是一个NP-hard问题，有很多启发式算法解决它，包括层次聚集、极值优化、模拟退火和谱算法等等。其中最流行的模块度优化算法是Louvain算法。

但是Louvain算法也可以优化其它质量函数比如Constant Potts Model(CPM), 其克服了模块度的一些缺点(分辨率限制)。

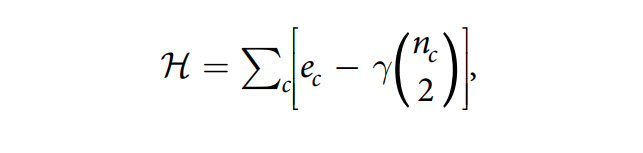
n代表节点的数目。γ的解释非常简单。参数的作用类似于一种阈值：社区的密度应至少为γ，而社区之间的密度应低于γ。分辨率越高，社区越多，分辨率越低，社区越少，这与模块化的分辨率参数类似。

分辨率限制：

论文出处：Fortunato, S. & Barthélemy, M. Resolution Limit in Community Detection. Proc. Natl. Acad. Sci. USA 104, 36, https://doi.org/10.1073/pnas.0605965104 (2007).

作者发现，即使在模块定义明确的情况下，模块优化也可能无法识别小于规模的模块，该规模取决于网络的总规模和模块的互连度。

we introduce a new algorithm that is faster, fnds better partitions and provides explicit guarantees and bounds. Te new algorithm integrates several earlier improvements, incorporating a combination of smart local move, fast local moveand random neighbour move.

Leiden算法集成了几个以前的改进，包括smart local move, fast local moveand random neighbour move(这三种算法最后有简单介绍)。

Louvain算法流程图如下：
Louvain首先将每个节点自己作为一个社区如图a)，然后将单个节点从一个社区移动到另一个社区中使得质量函数增加，得到图a的划分b)。然后基于此划分，进行凝聚操作，形成一个聚合网络c)，重复以上步骤，直到质量函数无法提高。

可以看做两个步骤：

1. 局部移动节点(模块度优化)
2. 凝聚网络

Louvain产生不良链接社区示意：

如图，假设将节点0移动到另一个节点，这个红色社区内部就变成了不连接的。但是对于节点1-6.它们仍然是局部最优分配的，所以他们仍然在红色社区内部。这个时候显然分裂为两个社区更好。但是Louvain算法不考虑这种情况，因为它只考虑单个节点的运动。

前面提到，由于分辨率限制，模块度可能会导致较小的社区聚集到较大的社区中。换句话说，模块度可能隐藏较小的社区。虽然CPM没有这个问题，然而，当CPM作为质量函数时，仍然会产生不良链接社区。所以，由于模块度分辨率限制以及不良连接，社区可能具有重要的子结构没被发现。

Louvain提供了两个保证：（1）没有社区可以合并，（2）没有节点可以移动。(多次迭代该算法，以前一次算法的社区划分结果作为后一次迭代的起点，直到无法进一步改进。) 但是多次迭代Louvain算法会使得不良连接问题更加明显，因为下一次的开始可能就会把上一轮结果中的桥节点(如上图0节点)移动到其他社区，使得社区内部的连接更差。

Leiden算法流程示意图：

Leiden算法从a开始，每个节点视为一个单独的社区，然后将单个节点从一个社区移动到另一个社区提高质量函数，以发现划分情况b。然后将b改善为c(节点所属的社区并没有改变)。基于改善后的分区c凝聚网络。使用未改善前的分区b为凝聚网络的社区划分情况（社区编号）。例如在b中的红色社区被改善为c中的两种节点，但都属于一个社区，算法凝聚后形成两个节点。然后算法继续移动凝聚后的网络节点，这个时候，f不会再改善分区结果。然后重复以上步骤，直到无法进一步改善。

可以看做三个步骤：

1. 局部移动节点
2. 改善划分结果
3. 基于改善后划分情况凝聚网络，基于未改善时划分情况初始化凝聚后网络（社区划分(社区编号)采取未改善时的网络划分情况）。

所以我们可以看到主要的不同就是Leiden算法添加了Refine步骤对划分结果进行改善。防止社区内部出现不良连接。

下图是Louvain算法与Leiden算法发现的连接不良的社区的百分比对比：

可以发现随着迭代次数的增加Leiden效果提升明显，而Louvain不良连接比例随着迭代次数还在增加，第4轮迭代后Leiden算法的不良连接社区率已经小于5%，而Louvain算法还是几十。而且我们需要注意的是，Leidien算法是保证社区是连通的，不存在不连通的社区。

社区的改善refine阶段：

首先将$P_{refined}$（正在改善的社区网络，前面的图C）中每个节点设为一个社区，然后开始$P_{refined}$中本地合并这些节点：在$P_{refined}$中独立的节点可以与其他社区合并。重要的是，合并仅在社区$P$(**改善前的网络，前面的图b)**中的各个社区内部中执行(不会改变社区编号（划分结果）)，此外，只有当节点和社区在$P$中连接良好的时候，才会将节点合并到社区中。在改善完成后，$P$中的社区通常会被改善为在$P_{refined}$中的多个社区，但并不总是如此。

在改善阶段，节点不一定会贪婪地与社区合并，不必使得质量函数得到最大增长。相反，一个节点可以和任何质量函数增大的社区合并，并且这种合并是随机选择的，质量函数的增加越大，社区被选择的可能性就越大。社区选择的随机性语序更加广泛地探索社区空间。只选择质量函数大于0 的社区，提高了算法速度，并且依然可以找到一组节点的最优划分(贪婪选择的话部分节点无法找到最优社区)。

Leiden算法和Louvain算法的另一个重要区别是局部移动阶段的实现。与Louvain算法不同，Leiden算法在这一阶段使用了快速的局部移动过程。Louvain不断访问网络中的所有节点，直到没有更多的节点移动来增加质量函数。在这样做的过程中，Louvain不断访问那些不能移动到其它社区的节点。在Leiden算法的快速局部移动过程中，只访问邻居发生变化(被移动到其他社区)的节点。

快速局部移动：

我们首先用网络中的所有节点初始化一个队列，节点入队的顺序是随机的。然后，从队列的前面删除第一个节点，并确定是否可以通过将该节点移动到其他社区来增加质量函数，增加则移动。如果我们将节点移动到其它社区，那么我们就将该节点的所有不属于它的新社区并且没在队列中的邻居节点添加到队列的尾部。我们不断的从队列前面移除节点，使这些节点可能移动到其它社区。重复执行，直到队列为空。

可以看到，快速局部移动过程，对网络中所有节点的第一次访问与Louvain算法相同。然而，在访问所有节点一次后，Leiden只访问邻居节点发生变化的节点(被移动到其他社区)，而Louvain继续访问网络中的所有节点。通过这种方式，Leiden比Louvain更有效地实现了局部移动阶段。

Leiden算法提供的保证：

Leiden算法通过迭代的运行，使用上一次迭代中识别的社区划分结果作为下一次迭代的起点。我们可以保证在迭代过程中的各个阶段发现的社区的许多性质。

Leiden算法每次迭代后，可以保证：

1. 所有的社区是γ-separated. (Louvain也保证)他指出当前分辨率下已经不存在可以合并的社区。

2. 所有的社区是γ-connected. (Louvain不保证)是普通连通性的加强变体。

   在这两个性质中，γ指的是优化的质量函数中的分辨率参数，可以是模块度或者CPM等。

   Leiden算法中，分区不变的迭代称为稳定迭代，在经过一次稳定迭代后，可以保证：

3. 所有节点是局部最优分配.（Louvain也保证）意味着没有单个节点可以再移动到其他社区。

4. 所有社区都是γ-dense的子分区。（Louvain不保证）一个社区是γ-dense的子分区，那么他可以被划分为两个部分：

   1. 两个部分相互连接良好.

   2. 任何一部分都不能与它的社区分离.

   3. 每个部分本生也是γ-dense子分区。

   子分区γ-dense并不意味着各个节点都是局部最优分配，他只是意味着个体节点与他们的社区连接良好。

   在Louvain算法中，一次稳定迭代之后，所有后续的迭代也将是稳定的，不能再有进一步的改进。而Leiden算法稳定迭代后，还可能在以后的迭代中进一步改进。当我们不断迭代Leiden算法，他会收敛到一个分区，并保证：

5. 所有社区均为均匀γ-dense。

6. 所有社区都是最优子集。

如果没有可以从社区中分离出来的子集，那么这个社区就是均匀的γ-dense的。均匀的γ-dense意味着无论一个社区如何划分为两个部分，这两个部分总是相互连接的很好。此外，如果一个分区中的所有社区都是均匀γ-dense的，那么分区的质量就离最佳不远了。如果社区的所有子集都是局部最优分配的，那么该社区就是最优子集。它的意思是，没有一个子集可以移动到不同的社区。子集最优性是Leiden算法提供的最强保证。它意味着均匀的γ-dense和上述所有其他性质。

下图为Louvain所发与Leiden算法所提供的保证：

Louvain和Leiden算法在不同经典网络种，经过10次迭代和10次重复实验后的最大模块度结果展示：

不良连接社区：

为了分析一个社区是否连接不良，我们可以在该社区所在节点组成的子网络上运行Leiden算法。运行Leiden算法，直到稳定迭代，当Leiden算法发现一个社区可以被分割为多个子社区(分割后模块度增加)，我们将该社区视为连接不良。通过计算被分割的社区的数量，我们可以得到连接不良社区的下界(因为就算Leiden算法没有找到子社区，也不能保证模块度不能通过分割社区增加，所以是下界)，连接不良的社区数也包括了不连接的社区数目。

Leiden算法伪代码：

代码可以直接调用Leiden库使用：

import igraph as ig
import leidenalg
import louvain

# 按照边列表的形式读入文件，生成无向图
g = ig.Graph.Read_Edgelist("data//OpenFlights.txt", directed=False)


part = leidenalg.find_partition(g, leidenalg.ModularityVertexPartition)
print(part)
print(ig.summary(g))
print(part.modularity)
ig.plot(part)

part2 = leidenalg.find_partition(g, leidenalg.CPMVertexPartition, resolution_parameter=0.01)
print(part2.modularity)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

smart local move

Waltman, L. & van Eck, N. J. A smart local moving algorithm for large-scale modularity-based community detection. Eur. Phys. J. B 86, 471, https://doi.org/10.1140/epjb/e2013-40829-0 (2013).

提出迭代Louvain算法，以上一次的结果作为下一次开始的划分情况，而不再是将节点自身看为一个节点。保证了社区合并局部最优与节点移动局部最优。

与Louvain算法一样，SLM算法一开始将网络中的每个节点分配它自己作为社区。与Louvain算法一样，SLM算法使用局部移动启发式算法来获得改进的社区结构。然而，在应用了局部移动启发式算法后，SLM算法采用了与Louvain算法不同的方法。 Louvain算法通过构建（凝聚）一个简化的网络来继续。SLM算法也会构造一个简化的网络，但在此之前，它首先要做一些其他的步骤。

SLM算法遍历当前社区结构中的所有社区。对于每个社区，构建一个所谓的子网。这是原网络的一个副本，其中只包括属于该社区的节点。然后，SLM 算法使用局部移动启发式算法来识别子网中的社区。首先将子网络中的每个节点分配到自己的单例社区，然后应用局部移动启发式算法。这样可能产生一个 包括子网中所有节点的大社区(这种情况相当于没变化)，其他情况下，获得了由多个社区组成的新的社区结构，每个社区包括子网中的一些节点（这种情况划分发生变化，相当于大社区被划分为多个小社区。）。

在获得子网的社区结构后，SLM算法开始凝聚一个缩减网络。凝聚网络中每个节点将与一个子网中的社区相对应(子网中的一个社区凝聚为一个节点，而不再是整个子网凝聚为一个节点)。对于同一子网中的社区们所凝聚形成的节点在凝聚网络中被分到一个社区（采用同样的社区编号，每个子网络中的节点还是在同一社区）。凝聚后的网络再进行下一次迭代，下一次迭代是基于上一次的凝聚网络，而不是原始的网络。（Leiden算法还要保证连通性好）

主要是在子网络中加入了局部移动，相当于对第一步结果进行了改善。后续这些节点还可能移动到其它社区，而在Louvain算法中 这些节点不会再移动到其它社区了

传统的Louvain在多次迭代后很容易收敛，不能再通过合并社区或将单个节点从一个社区移动到另一个社区得到改善，而SLM能进行更多的迭代，通过分割社区或者将节点集从一个社区移动到另一个社区不断寻找增加模块度的可能性。

fast local move

Ozaki, N., Tezuka, H. & Inaba, M. A Simple Acceleration Method for the Louvain Algorithm. Int. J. Comput. Electr. Eng. 8, 207–218, https://doi.org/10.17706/IJCEE.2016.8.3.207-218 (2016).

Louvain Prune剪枝算法，计算时间显著缩短，可达90%。

Louvain算法花费大量的时间在第一阶段，移动节点优化模块度。

这是由于每个阶段1循环对图中所有节点的所有相邻节点计算∆Q造成的，尽管只有极少数节点在几次阶段1循环后改变其社区，所以大量的阶段1循环会使算法变慢。

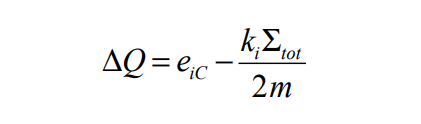
如果我们能够在阶段1中识别出将改变其社区的节点，并在第一阶段只考虑它们，计算时间将显著减少。虽然无法准确识别，但我们可以通过表达式来缩小未来有可能改变社区的节点。∆Q的每一个值都是通过其他节点的社区转换而改变的。然而，一个节点的社区转变只对其邻居的节点、邻居社区的节点和新社区的节点产生∆Q。因此，当节点更换社区时，我们可以将∆Q较高的节点标记。因此，在阶段1中只考虑这些节点，应该会减少流程中的低效率操作。
根据公式可以看到，如图几种邻域节点会改变∆Q。

1. 将所有节点放入p中
2. 随机选择一个进行访问
3. 遍历v的可能改变的邻域节点(Leiden只添加了邻居节点)
4. 找到模块度改变最大的节点所在的社区
5. 将节点v移动到改变最大节点所在的社区
6. 找到n的所有可能改变且不再v所在社区的节点
7. 将他们添加到p中
8. 继续迭代 直到p为空

random neighbour move

Traag, V. A. Faster unfolding of communities: Speeding up the Louvain algorithm. Phys. Rev. E 92, 032801,

Random Neighbor Louvain Algorithm (hereafter RNL) 随机邻居Louvain算法，第一阶段，移动节点时，RNL随机选择一个邻居节点的社区，而不是选出最好的相邻社区。而且并不会影响结果的准确性，这意味着即使我们随机选择邻居节点，它也有很高的概率在同一个社区中。

这种改善是由于两个因素:(1)随机邻居很可能是一个“好”社区(使质量函数增加的社区)，(2)随机邻居很可能是一个枢纽，有助于收敛。

在初始分区中，每个节点都在自己的社区中，几乎所有相邻社区移动都是一种改进。此外，当算法稍微进步一点时，许多邻居可能属于同一个社区。因此，作者建议不考虑所有的邻居社区，而是简单地选择一个随机邻居，并考虑该社区，称其为随机邻居Louvain。