深度强化学习系列(16): 从DPG到DDPG算法的原理讲解及tensorflow代码实现_dpg和ddpg

1、背景知识

在前文系列博客第二篇中讲解了DQN（深度强化学习DQN原理），可以说它是神经网络在强化学习中取得的重大突破，也为强化学习的发展提供了一个方向和基础，Sliver等人将其应用在Atari游戏中取得了重大突破, 后来大批量的论文均采用了DQN的思想，同时提出了更多的但是该算法有以下缺点:

Atari 游戏所需的动作是离散的，且属于低维（只有少数几个动作），但现实生活中很多问题都是连续的，且维度比较高，比如机器人控制（多个自由度）、汽车方向盘转向角度，油门大小、天气预报推荐指数等。虽然可以对连续性高维度的动作做离散型的处理，但是对于一个经过离散处理的大状态空间，使用DQN训练仍然是仍然是一个比较棘手的问题，因为DQN算法的核心思想是利用随机策略进行探索，对于高维度的来说，第一个问题是：模型很难收敛，第二个问题是需要在探索和利用之间进行协调。

因此用DQN解决高维度连续状态空间的任务变得非常的困难。为了解决该问题，David Sliver在2014年ICML大会论文中提出了确定性策略梯度((Deterministic Policy Gradient Algorithms)), 是的，这就是福音！下面先从DPG算法开始，然后再说Deep DPG(DDPG)

1、确定性策略梯度(Deterministic policy gradient )

首先解决一个强化学习问题，我们想到的就是累计折扣奖励的定义，即状态满足${\rho }^{\pi }$ 分布上的累计奖励，如下：
$$\begin{gathered} {\nabla }_{\theta }J({\pi }_{\theta })={\int }_S{\rho }^{\pi }(s){\int }_A{\pi }_{\theta }(a|s)r(s,a)dads \\ =E_{s\sim {\rho }^{\pi },a\sim {\pi }_{\theta }}[r(s,a)] \end{gathered}$$
那么什么是策略梯度呢？策略梯度就是沿着使目标函数变大的方向调整策略的参数，它被定义为：

$$\begin{gathered} {\nabla }_{\theta }J({\pi }_{\theta })={\int }_S{\rho }^{\pi }(s){\int }_A{\nabla }_{\theta }{\pi }_{\theta }(a|s)Q^{\pi }(s,a)dads \\ =E_{s\sim {\rho }^{\pi },a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{\pi }(s,a)] \end{gathered}$$
公式非常直白的告诉我们，J()函数主要与策略梯度和值函数的期望有关，尽管状态空间分布${\rho }^{\pi }$的分布依赖于策略参数，但是策略梯度并不依赖于状态分布上的梯度。另外，在DQN中我们使用了评价网络和target网络，采用了experimence replay的方式打乱了数据之间的相关性而使得满足独立同分布条件，利用softupdating方式更新target网络，但总结一句话，它的策略网路和值函数网络使用的是同一个网络。在DPG的公式表明，J()和策略梯度与值函数有关，因此为了解决策略和值函数之间的问题，采用了一种新的解决思路将两个网络分开，即：Actor-critic异步框架。

1.1 、Actor-critic框架

从框架的 名字我们就可以知道一些信息：Actor(演员)-Critic(评论家)框架，相当于演员和评论家共同来提升表演，演员跳舞的姿态可能动作不到位，于是评论家告诉演员，你这样跳舞不好，它会建议演员修改一下舞姿了，当演员在某个舞姿上表演的比较好，那评论家就会告诉演员, 不错，你可以加大力度往这个方向发展，是不是明白其中的意思了？
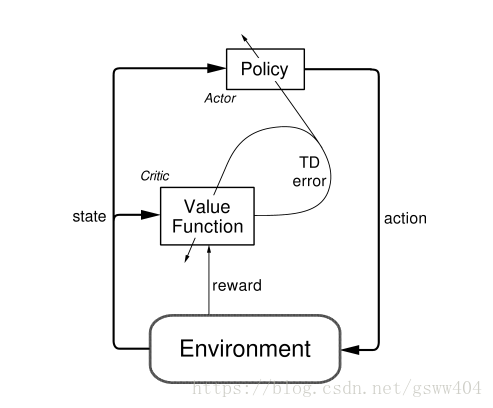
那么对应到RL中，Actor就是策略网络，来做动作选择(空间探索)。Critic就是值函数，对策略函数进行评估， 具体的流程如图：

简单描述一下图：其中的TD-error就是Critic告诉Actor的偏差。
具体的更新过程：
$$\begin{gathered} {\delta }_t=r_t+\gamma Q^w(s_{t+1},{\mu }_{\theta }(s_{t+1}))-Q^w(s_t,a_t) \\ {w}_{t+1}=w_t+{\alpha }_w{\delta }_t{\nabla }_w{Q}^w(s_t,a_t) \\ {\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{\mu }_{\theta }(s_t)\nabla Q^w(s_t,a_t){|}_{a={\mu }_{\theta }(s)} \end{gathered}$$

我们现在考虑如何将策略梯度框架扩展到确定性政策。 我们的主要结果是一个确定性的策略梯度定理，类似于上一节中介绍的随机政策梯度定理。 我们在确定性政策梯度的形式背后提供一种非正式的直觉。 然后，我们从第一原则给出确定性政策梯度定理的形式证明。 最后，我们证明确定性政策梯度定理实际上是随机政策梯度定理的一个极限情况（具体的证明见论文附录）
那么极限情况是啥呢？就是当概率策略的方差趋近于0的时候，就是确定性策略,即
$$\begin{gathered} {\nabla }_{\theta }J({\mu }_{\theta })={\int }_S{\rho }^{\mu }(s){\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}ds \\ =E_{s\sim {\rho }^{\mu }}[{\nabla }_{\theta }{\mu }_{\theta }(s)\nabla Q^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}] \end{gathered}$$
公式推到依据： 对于连续性变量，期望通过积分求得：
$$E_{x\sim P}[f(x)]=\int p(x)f(x)dx$$

1.2 兼容函数近似

一般而言，将近似$Q^w(s,a$代入确定性政策梯度并不一定会遵循真正的梯度（事实上它也不一定是上升方向）。 类似于随机情况，我们现在找到一类兼容函数逼近器$Q^w(s,a$，使得真正的梯度被保留。 换句话说，我们找到了 critic $Q^w(s,a$，使得梯度${\nabla }_a{Q}^{\mu }(s,a)$可以用${\nabla }_a{Q}^w(s,a)$替代，而不会影响确定性政策梯度。 以下定理适用于on-policy $E[\cdot ]=E_{s\sim {\rho }^{\mu }}[\cdot ]$和off-policy政策，$E[\cdot ]=E_{s\sim {\rho }^{\beta }}[\cdot ]$,

总结一下：
回顾前文的内容，我们知道广义的值函数求解包括策略评估和策略改善，当值函数最优的饿时候，策略也是最优的（此处的策略是贪婪策略），而策略搜索是将策略参数化，即${\pi }_{\theta }(s)$, 因此，我们可以使用参数化或者非参数化(神经网路) 逼近策略，找到最优的$\theta$, 使得累计折扣奖励最大化。确定性策略梯度就是在确定的梯度策略方向上进行学习。

---

2、深度确定性策略（DDPG）

感兴趣的可以看看原文《continuous control with deep reinforcement learning》
之所以使用确定性策略的原因是相对与随机策略，就是因为数据的采样少，算法效率高，深度确定性策略就是使用了深度神经网络去近似值函数和策略梯度网络。总结一下DDPG算法使用以下核心思想：
（1）采用经验回放方法
（2）采用target目标网络更新（为什么要用target网络？因为训练的网络特别不稳定）
（3）AC框架
（4）确定性策略梯度

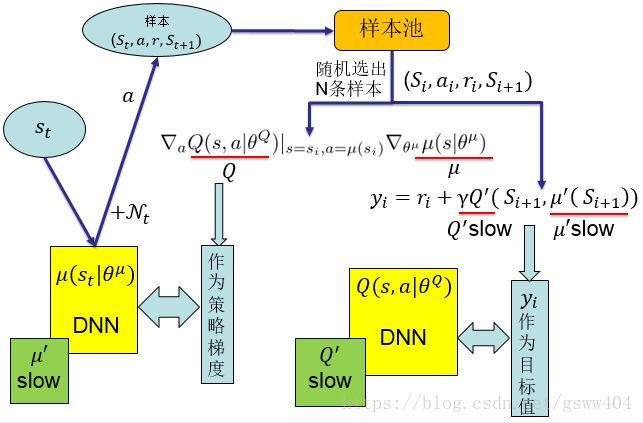
2.1、DDPG算法流程图

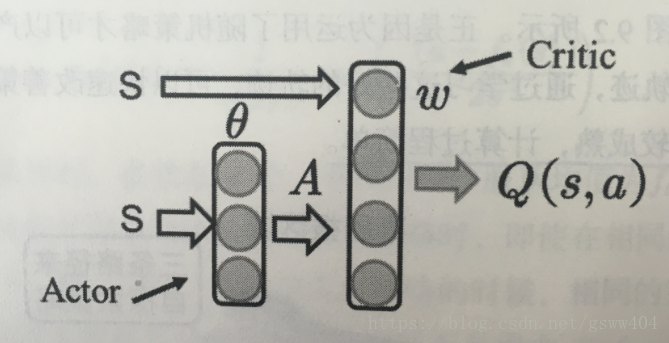
算法采用AC框架，Actor获取状态$S$, s可以是一组向量（速度，位置等），经过Actor网络选取动作action，Critic根据动作action和S进行评价，采用策略梯度最终更新两个网络的权重。具体见下文：

2.2、DDPG算法原理

DPG算法通过确定性地将状态映射到特定动作来维护指定当前策略的参数化参与者函数$\mu (s|{\theta }^{\mu })$。 评论者$Q(s,a)$是在Q学习中使用Bellman方程学习的。 通过将链规则应用于从起始分布J相对于参数参数的预期回报来更新参与者，原理部分尽量少对公式，下面我们结合算法伪代码详细解释，：

（1）初始化网络

第1行：首先随机初始化了Actor网络$\mu (s|{\theta }^{\mu })$ 和Critic网络Q(s, a)
第2行：初始化target网络，它的结构和actor和critic的一样，并且参数也一样，相当于复制了一份
第3行：初始化Replay Buffer R,因为强化学习的马尔科夫序列之间的数据具有非常大的关联性，采用R的目的就是打乱数据之间的相关性，使得数据之间满足独立同分布。

#####（2）训练Episode
第5行：初始化一个随机的N,它相当于动作空间的探索度，后面讲解
第6行：获得观察指$s_1$
第8行：选取动作，这个动作是由两部分组成：1、策略网络$\mu$的输出+ 探索度(确保有足够的探索度，避免灭有学习到足够多的知识)
第9行：执行代码，根据观察值$s_t$ 和动作，执行action，得到对应的奖励R和$s^{{}^{\prime }}$

存储和读取Replay Buffer R

第10，11行：将学习的序列存储到R中，然后随机批量的读取R中的序列进行学习模型。
注：由于强化学习过程学习过程的序列之间有相关性，一般随机批量的batch-size= 64,128,256（原因是根据计算机内存或者显存，具体参考：https://danluu.com/3c-conflict/）

更新Critic网络结构

第12，13行，首先定义了$y_i$, 这里使用了RMSE误差，更新的时候直接更新值函数的损失。

更新Actor网络结构

第15行：此处直接更新的也是Actor策略梯度

更新目标target网络的参数

最后两行采用了DQN的soft updating 方式更新目标网络，即用$\tau$ 来延迟更新。

---

最后的最后， 用一张图总结一下：

---

代码实现：

本部分对gym中的立杆（Pendulum-v0）进行代码讲解,效果图如下，其中gym的安装详见github：https://github.com/openai/gym

注：直接可以粘贴在pycharm中使用（切记把编码改为utf-8，否则中文注释出错）

import tensorflow as tf
import numpy as np
import gym
import time

# 定义超参数
MAX_EPISODES = 200
MAX_EP_STEPS = 200
LR_A = 0.001    # actor学习率
LR_C = 0.002    # critic学习率
GAMMA = 0.9     # 累计折扣奖励因子
TAU = 0.01      # 软更新tao
MEMORY_CAPACITY = 10000  # buffer R, 经验回放容器
BATCH_SIZE = 32  # 每批随机读取批次大小

RENDER = False
ENV_NAME = 'Pendulum-v0'

# 定义DDPG类
class DDPG(object):
    def __init__(self, a_dim, s_dim, a_bound,):
        # memory 存放的是序列（s,a,r,s+1）= s*2+a+1(r=1)
        self.memory = np.zeros((MEMORY_CAPACITY, s_dim * 2 + a_dim + 1), dtype=np.float32)
        self.pointer = 0
        self.sess = tf.Session()

        self.a_dim, self.s_dim, self.a_bound = a_dim, s_dim, a_bound,
        self.S = tf.placeholder(tf.float32, [None, s_dim], 's')
        self.S_ = tf.placeholder(tf.float32, [None, s_dim], 's_')
        self.R = tf.placeholder(tf.float32, [None, 1], 'r')
        
        # 建立网络，actor网络输入是S,critic输入是s,a
        self.a = self._build_a(self.S,)
        q = self._build_c(self.S, self.a, )
        
        a_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Actor')
        c_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Critic')
        # soft updating
        """
        tf.train.ExponentialMovingAverage(decay)是采用滑动平均的方法更新参数。这个函数初始化需要提供一个衰减速率（decay），用于控制模型的更新速度。这个函数还会维护一个影子变量（也就是更新参数后的参数值），这个影子变量的初始值就是这个变量的初始值，影子变量值的更新方式如下：
   shadow_variable = decay * shadow_variable + (1-decay) * variable
   shadow_variable是影子变量，variable表示待更新的变量，也就是变量被赋予的值，decay为衰减速率。decay一般设为接近于1的数（0.99,0.999）。decay越大模型越稳定，因为decay越大，参数更新的速度就越慢，趋于稳定。
        """
        
        ema = tf.train.ExponentialMovingAverage(decay=1 - TAU)          # soft replacement
        def ema_getter(getter, name, *args, **kwargs):
            return ema.average(getter(name, *args, **kwargs))

        target_update = [ema.apply(a_params), ema.apply(c_params)]      # soft update operation
        a_ = self._build_a(self.S_, reuse=True, custom_getter=ema_getter)   # replaced target parameters
        q_ = self._build_c(self.S_, a_, reuse=True, custom_getter=ema_getter)

        a_loss = - tf.reduce_mean(q)  # maximize the q
        self.atrain = tf.train.AdamOptimizer(LR_A).minimize(a_loss, var_list=a_params)

        with tf.control_dependencies(target_update):    # soft replacement happened at here
            q_target = self.R + GAMMA * q_
            td_error = tf.losses.mean_squared_error(labels=q_target, predictions=q)
            self.ctrain = tf.train.AdamOptimizer(LR_C).minimize(td_error, var_list=c_params)

        self.sess.run(tf.global_variables_initializer())
    
    # 选取动作函数
    def choose_action(self, s):
        return self.sess.run(self.a, {self.S: s[np.newaxis, :]})[0]
    
    # 从R buffer中学习
    def learn(self):
        indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE)
        bt = self.memory[indices, :]
        bs = bt[:, :self.s_dim]
        ba = bt[:, self.s_dim: self.s_dim + self.a_dim]
        br = bt[:, -self.s_dim - 1: -self.s_dim]
        bs_ = bt[:, -self.s_dim:]

        self.sess.run(self.atrain, {self.S: bs})
        self.sess.run(self.ctrain, {self.S: bs, self.a: ba, self.R: br, self.S_: bs_})
  
    # 存储序列
    def store_transition(self, s, a, r, s_):
        transition = np.hstack((s, a, [r], s_))
        index = self.pointer % MEMORY_CAPACITY  # replace the old memory with new memory
        self.memory[index, :] = transition
        self.pointer += 1
   
    # 建立actor网络（输入S_dim，输出a_dim, 采用tanh激活函数）
    def _build_a(self, s, reuse=None, custom_getter=None):
        trainable = True if reuse is None else False
        with tf.variable_scope('Actor', reuse=reuse, custom_getter=custom_getter):
            net = tf.layers.dense(s, 30, activation=tf.nn.relu, name='l1', trainable=trainable)
            a = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, name='a', trainable=trainable)
            return tf.multiply(a, self.a_bound, name='scaled_a')
    
    # 建立critic网络（输入S_dim，s_dim, 输出q）
    def _build_c(self, s, a, reuse=None, custom_getter=None):
        trainable = True if reuse is None else False
        with tf.variable_scope('Critic', reuse=reuse, custom_getter=custom_getter):
            n_l1 = 30
            w1_s = tf.get_variable('w1_s', [self.s_dim, n_l1], trainable=trainable)
            w1_a = tf.get_variable('w1_a', [self.a_dim, n_l1], trainable=trainable)
            b1 = tf.get_variable('b1', [1, n_l1], trainable=trainable)
            net = tf.nn.relu(tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1)
            return tf.layers.dense(net, 1, trainable=trainable)  # Q(s,a)


# training process

# 环境初始化
env = gym.make(ENV_NAME)
env = env.unwrapped
env.seed(1)

# 获取s,a的维度
s_dim = env.observation_space.shape[0]
a_dim = env.action_space.shape[0]
a_bound = env.action_space.high

ddpg = DDPG(a_dim, s_dim, a_bound)

var = 3  # 定义探索因子

t1 = time.time()
for i in range(MAX_EPISODES):
    s = env.reset()
    ep_reward = 0
    for j in range(MAX_EP_STEPS):
        if RENDER:
            env.render()

        # 添加探索噪音
        a = ddpg.choose_action(s)
        a = np.clip(np.random.normal(a, var), -2, 2)    # 随机选取动作探索
        # np.clip()函数是，如果随机生成的数字大于2，则为2 ，如果小于-2，则为-2，其他则为本身
        
        s_, r, done, info = env.step(a)
        ddpg.store_transition(s, a, r / 10, s_)

        if ddpg.pointer > MEMORY_CAPACITY:
            var *= .9995    # 减缓动作探索度，即衰减速率
            ddpg.learn()

        s = s_
        ep_reward += r
        if j == MAX_EP_STEPS-1:
            print('Episode:', i, ' Reward: %i' % int(ep_reward), 'Explore: %.2f' % var, )
            # if ep_reward > -300:RENDER = True
            break

print('Running time: ', time.time() - t1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

注：此处没有保存模型，tf采用saver保存和调用模型，后期会在其他模型中添加。

参考资料：
[1].https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/6-2-DDPG/
[2].https://zhuanlan.zhihu.com/p/28549596
[3].https://blog.csdn.net/kenneth_yu/article/details/78478356