- 1Linux查看网络带宽使用情况_linux网卡使用率百分比
- 2使用 Flutter 打造引人入胜的休闲游戏体验
- 3ananconda环境中,出现SSLError报错_conda sslerror
- 4python远程文件管理系统_python 读取远程服务器文件
- 5自制【平衡小车】程序篇——基于STM32核心_stm32平衡小车pid算法程序
- 6关于camera:基于S12单片机的循迹小车视觉系统设计与优化_像素帧数小车
- 7做ROS小车实物的第一天_用ros做一个实物出来要多久
- 8数据结构之链表练习题(leetCode)_先将键盘输入的一组整数依次存入循环链表(尾插法),然后删除头部第一个元素,最后将
- 9Debezium系列之:Debezium2.X之Oracle数据库的Debezium连接器_io/debezium/connector/oracle/rest/debeziumoracleco
- 10Docker容器中的OpenCV:轻松构建可移植的计算机视觉环境_容器中显示cv::imshow
3 随机数与蒙特卡洛方法及Python实现_python 蒙特卡罗生成数据
赞
踩
0 建议学时
4学时
1 引入
1.1 随机数与采样
客观世界的某些行为,结果具有随机性:
- 掷骰子、投硬币;
- 等待公交车的时间;
- 种子发芽的比例;
1.2 随机数函数
1.2.1 random模块
Python的random模块中提供了若干生成随机数的函数:
如random.random()可以产生区间[0,1)内的一个随机数
import random
random.random() 0.2865887089067386
random.random() 0.613263367620591
random.random() 0.04800896336544469
- 1
- 2
- 3
- 4
注意:计算机只能产生’‘伪随机数’',这些随机数本身仍然是由一个确定的算法生成的。
关于random库
- random.random() 产生均匀分布于[0, 1)的随机数
- random.uniform(a,b) 产生均匀分布于[a, b)的随机数
# 生成100个[-1, 1)的随机数
import random
N = 100
x = range(N)
y = [random.uniform(-1, 1) for item in x]
- 1
- 2
- 3
- 4
- 5
for语句简写
[x for x in range(10)]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[x+3 for x in range(10)]
[3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
- 1
- 2
- 3
- 4
- 5
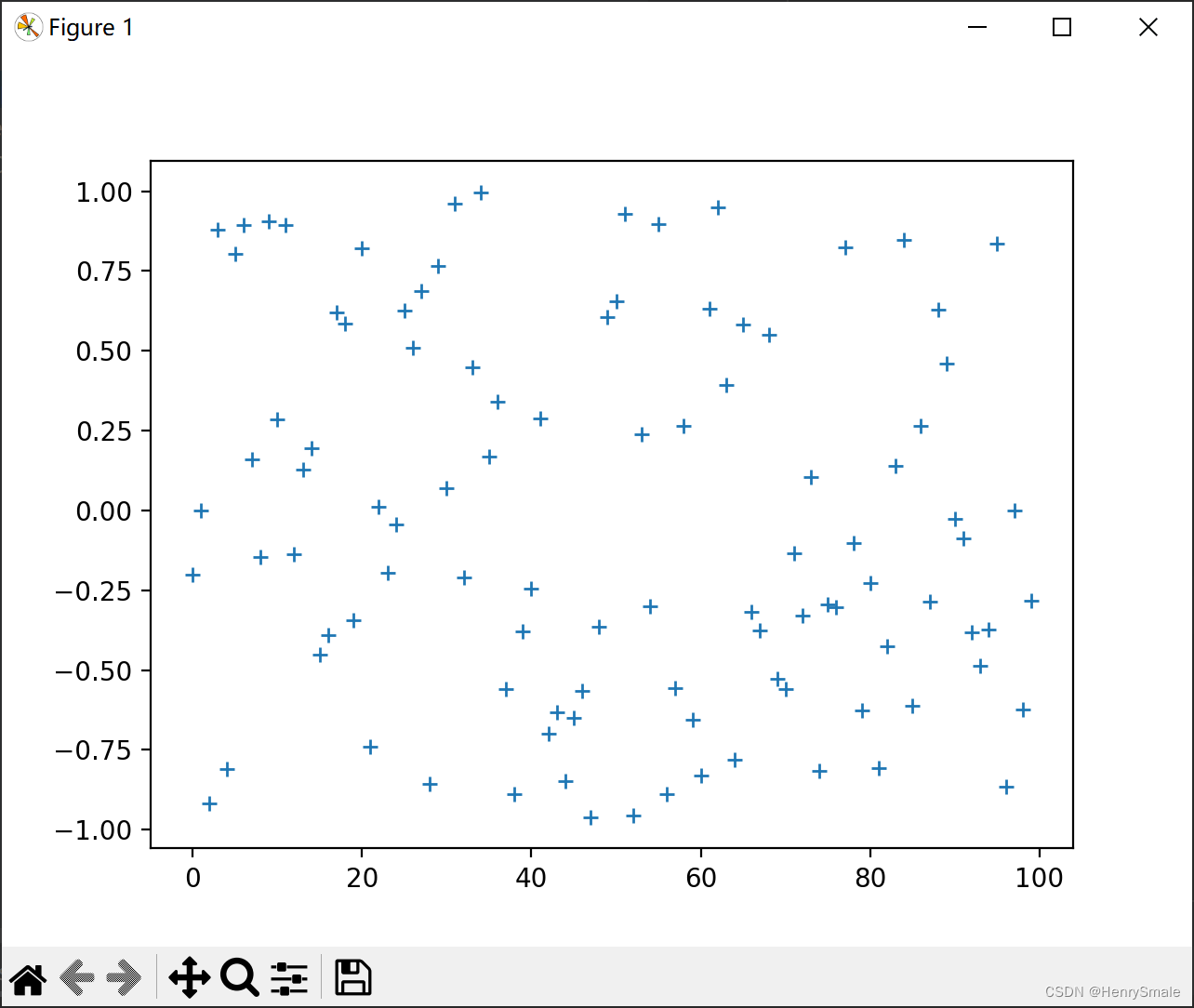
随机函数的使用
import matplotlib.pyplot as plt
import random
N = 100
x = range(N)
y = [random.uniform(-1, 1) for item in x]
plt.plot(x, y, '+')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
1.2.2 批量产生随机数
random库中的random函数每次只能产生单个随机数
使用numpy库的random模块可以一次性生成大量的随机数
from numpy import np
np.random() #0.37452288986512927
array = np.random(size=5)
print(array) #array([0.93312885, 0.70160214, 0.9727459, 0.1363383,0.54146683])
np.uniform(-1,1) #0.8232171988008607
array = np.uniform(-1,1,size=5)
print(array) #array([ 0.94529425,-0.6128988,0.29927762,0.65928358,0.11272987])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
1.3 Numpy
- Numpy:Numerical Python,Numpy是高性能科学计算和数据分析的基础包,其部分功能如下:
– ndarray,一个具有矢量算术运算和复杂广播能力的快速且节省空间的多维数组。
– 用于对整组数据进行快速运算的标准数学函数(无需编写循环)。
– 用于读写磁盘数据的工具以及用于操作内存映射文件的工具。
– 线性代数、随机数生成以及傅里叶变换功能。
– 用于集成由C、C++、Fortran等语言编写的代码的工具。



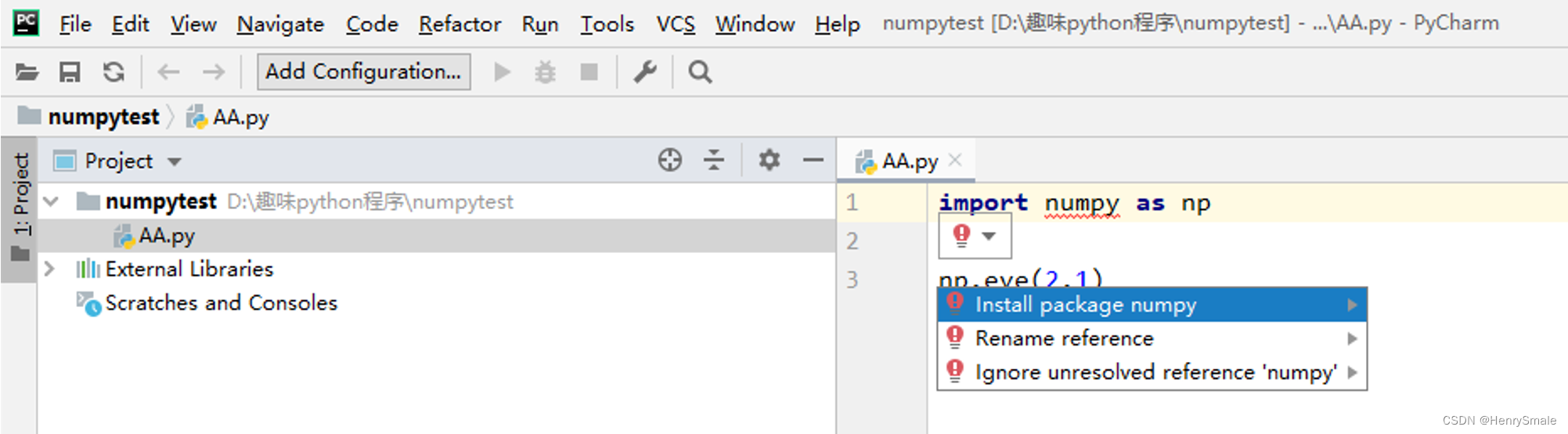
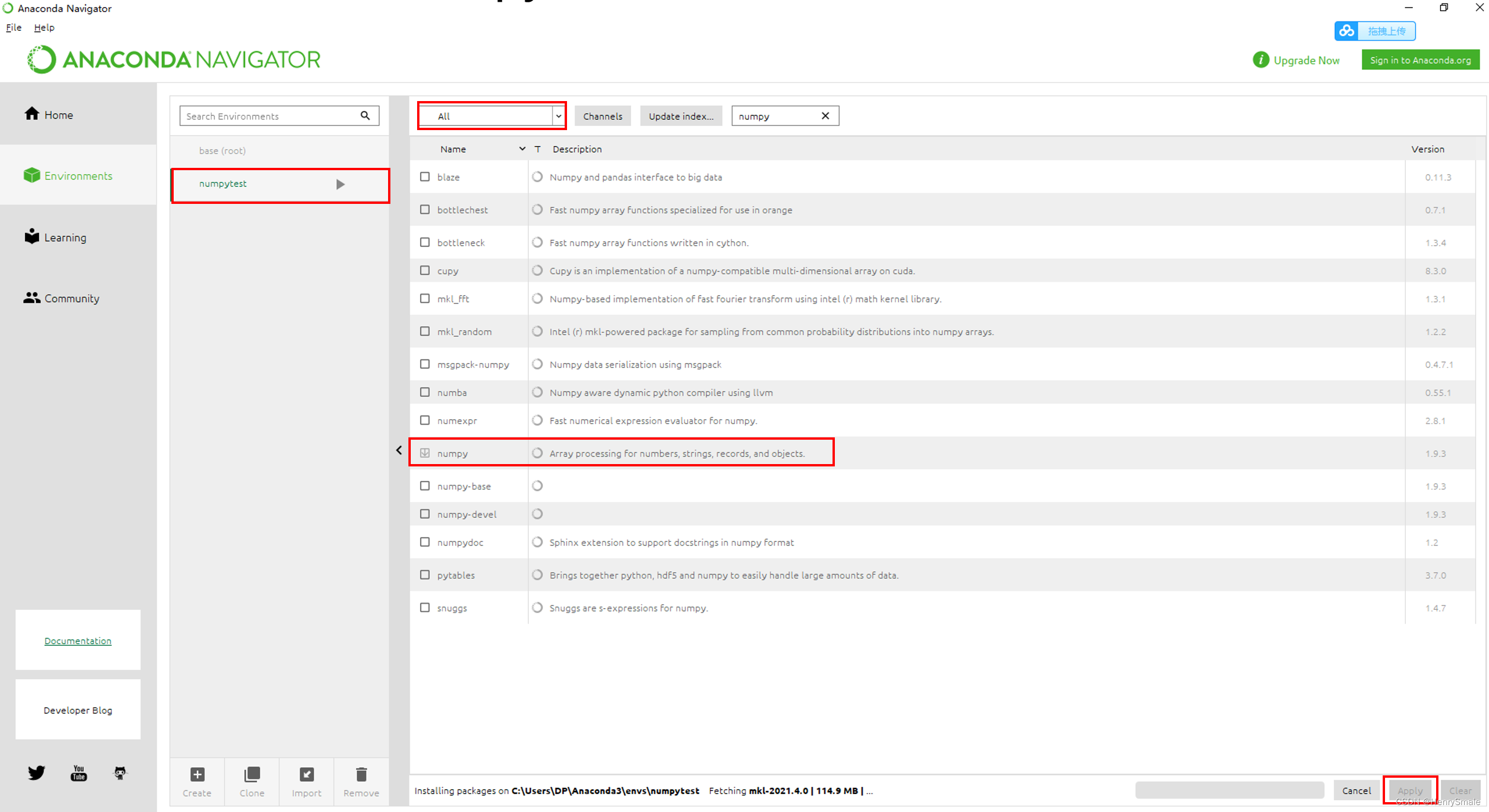
1.3.1 安装Numpy
1.3.2 生成ndarray
最简单的方法就是使用array函数。array函数接收任何的序列型对象(当然也包括其他的数组),生成一个新的包含传递数组的numpy数组。例如:
import numpy as np
data1 = [6, 7.5, 8, 0, 1]
arr1 = np.array(data1)
arr1
array([ 6. , 7.5, 8. , 0. , 1. ])
- 1
- 2
- 3
- 4
- 5
嵌套序列,例如同等长度的列表,将会自动转换成多维数组
data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr2 = np.array(data2)
arr2
array([[1, 2, 3, 4],
[5, 6, 7, 8]])
- 1
- 2
- 3
- 4
- 5
通过ndim和shape可以查看属性:
arr2.ndim
2
arr2.shape
(2, 4)
- 1
- 2
- 3
- 4
1.3.3 arange(): 创建数组
import numpy as np
array = np.arange(5) #左闭右开[0,5)
print(array) #[0 1 2 3 4]
array = np.arange(1, 5) #左闭右开[1,5)
print(array) #[1 2 3 4]
array = np.arange(0, 1, 0.1)
print(array) #[0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
1.3.4 zeros和ones
zeros和ones分别可以创建指定长度或者形状的全0或全1数组
array = np.zeros((3, 2))
[[0. 0.]
[0. 0.]
[0. 0.]]
array = np.ones((3, 2))
print(array)
[[1. 1.]
[1. 1.]
[1. 1.]]
array = np.eye(2)
print(array)
[[1. 0.]
[0. 1.]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
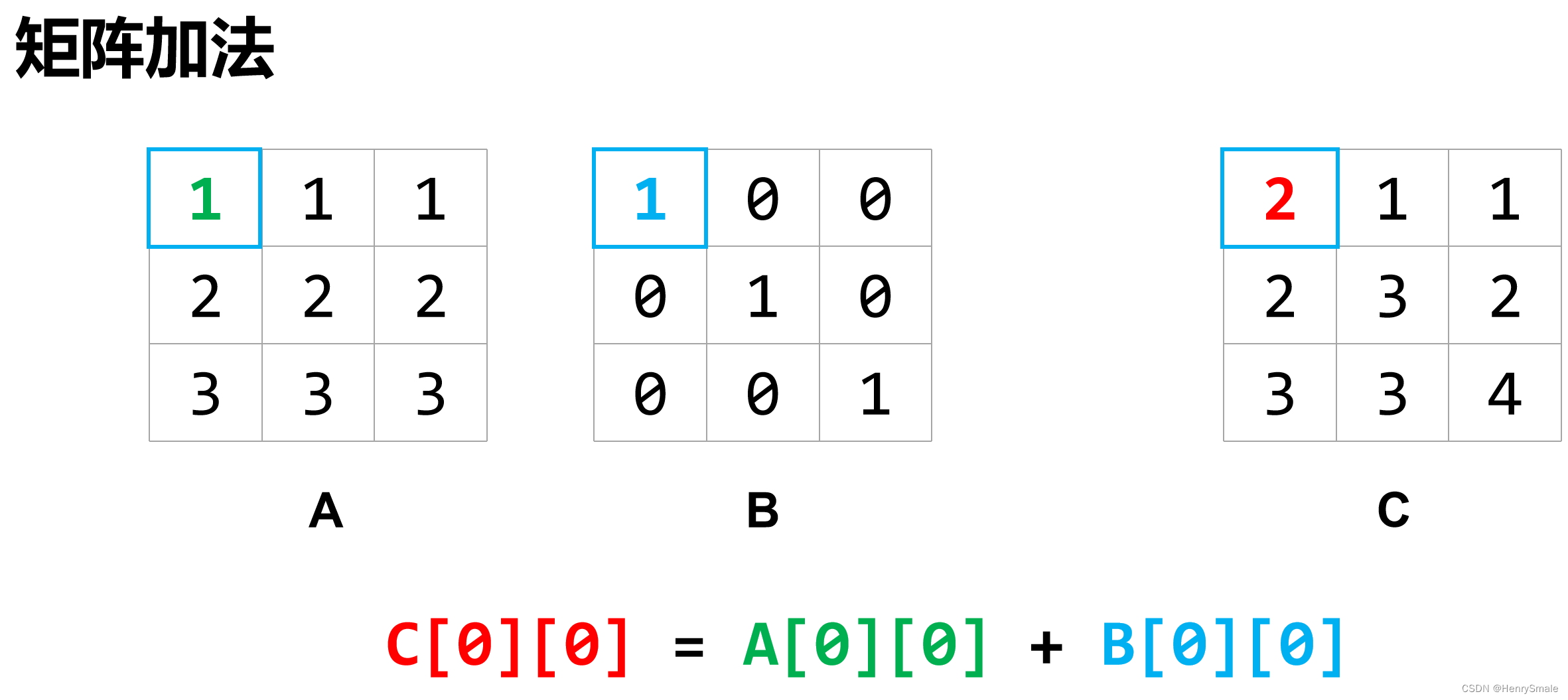
1.3.5 Numpy运算
import numpy as np
x=np.array([1,2,3,4,5]) #[1,2,3,4,5]
x=x*2 #[2,4,6,8,10]
print(x>5) #[False,False,True,True,True]
- 1
- 2
- 3
- 4
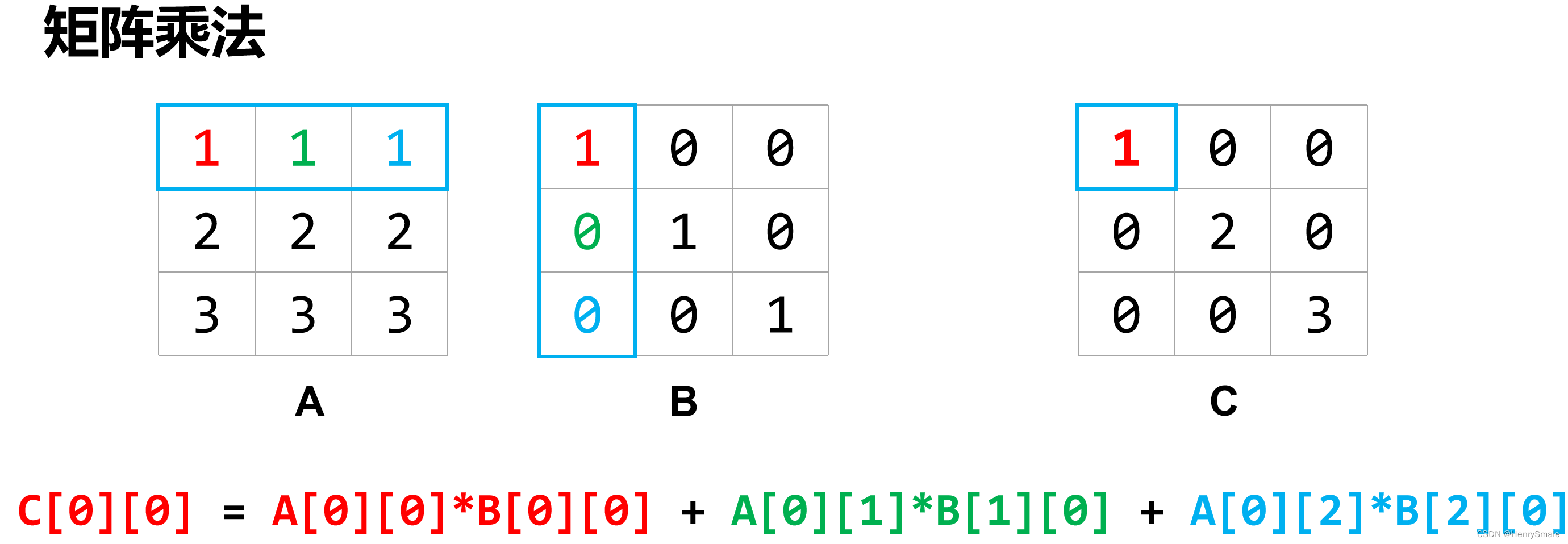
1.3.6 Numpy库速度对比
"for _ in range(n)“用于循环n次,不用设置变量,用”_"指代临时变量,只在这个语句中使用一次。
import numpy as np
import time
my_arr = np.arange(1000000)
my_list = list(range(1000000))
beginTime = time.perf_counter()
for _ in range(10):
my_arr2 = my_arr * 2
tNp = time.perf_counter() -beginTime
beginTime = time.perf_counter()
for _ in range(10):
my_list2 = [x * 2 for x in my_list]
tList = time.perf_counter() -beginTime
print("tNp = ", tNp)
print("tList = ", tList)
# tNp = 0.009103899999999998 (9ms)
# tList = 0.3303001 (330ms)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
1.3.7 批量产生随机数
[a,b]之间的随机整数
random和numpy都提供了整型随机数函数
import random
r=random.randint(1,100) #[1,100],包含100
import numpy as np
r=np.random.randint(1,100,10) #[1,100),不包含100
# array([33, 53, 24, 12, 49, 24, 63, 74, 29, 94])
r=np.random.random_integers(1,100,10) #[1,100],包含100
# array([21, 32, 54, 17, 47, 84, 52, 76, 100, 73])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
示例:统计掷骰子出现某点数的频率
掷一枚骰子会随机出现1-6点,掷10000次,出现6的概率是多少?
import random
N = 10000
lt = [random.randint(1, 6) for i in range(N)]
M = lt.count(6)
print('6点%d次,共掷了%d次' % (M, N))
print('出现6点的概率:', M/N)
- 1
- 2
- 3
- 4
- 5
- 6
使用numpy
import numpy as np
N = 10000
lt = np.random.randint(1, 7, N)
six = [i for i in lt if i == 6]
print('6点%d次,共掷了%d次' % (len(six), N))
print('出现6点的概率:', len(six)/N)
- 1
- 2
- 3
- 4
- 5
- 6
掷骰子(使用随机数组):使用数组比较和numpy中的数组求和更高效
import numpy as np
N = 10000
eyes = np.random.randint(1, 7, N) #利用随机数构建列表eyes
success = eyes == 6 #构建一个列表success,存储bool类型
M = np.sum(success)
print('6点%d次,共掷了%d次' % (M, N))
print('出现6点的概率:', M/N)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
1.3.8 随机数程序的调试
随机数程序的调试困难,因为每次执行会生成不同的数据序列
可以设置随机种子,使随机数的生成序列固定random.seed(10)
缺省情况下,系统以当前时间作为种子
import random
random.seed(10)
['%.3f' % random.random() for i in range(6)]
#['0.571', '0.429', '0.578', '0.206', '0.813', '0.824']
random.seed(10)
['%.3f' % random.random() for i in range(6)]
#['0.571', '0.429', '0.578', '0.206', '0.813', '0.824']
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
2 蒙特卡洛(Monte Carlo)方法
2.1 问题引入
如何求不规则图形的面积?
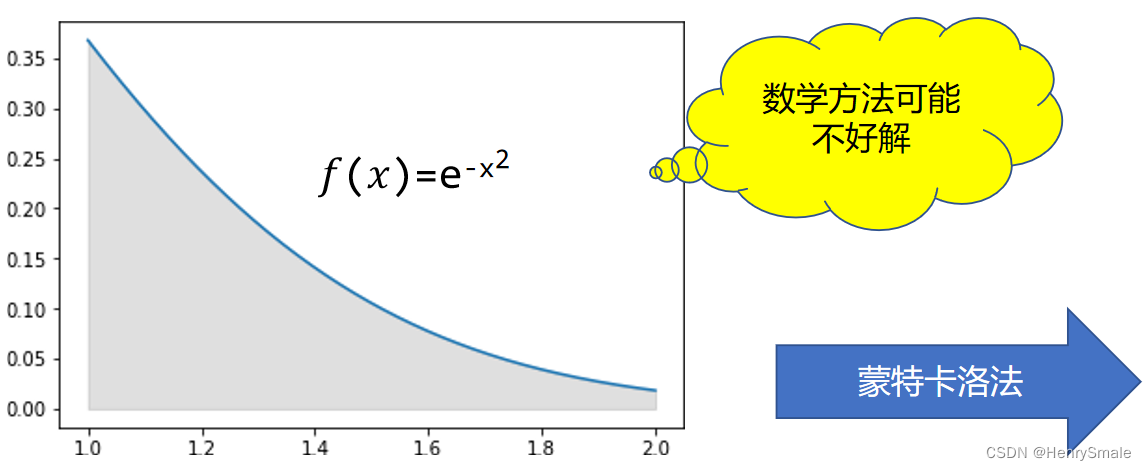
应用:蒙特卡洛剂量计算被广泛视为放疗领域,剂量计算金标准。通过随机模拟大量粒子与物质相互作用的全过程,蒙特卡洛方法准确计算,反映了真实的剂量分布,可以实现5分钟内快速准确的蒙特卡洛剂量计算,剂量计算的统计偏差小于2%。
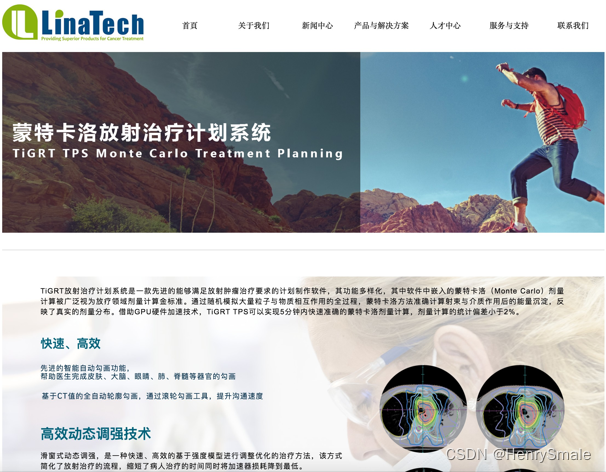
常见应用:
- 估算某事件发生的概率;
- 估算不规则区域的面积/体积;
- 蒙特卡洛积分。
2.2 方法介绍
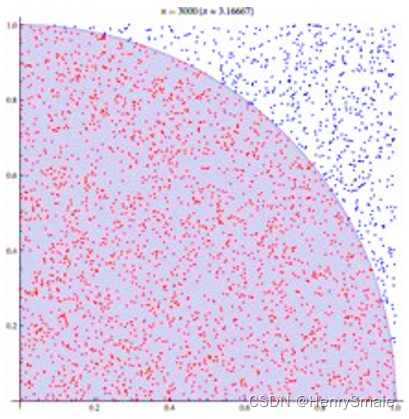
基本思想:通过随机抽样的方法,以随机事件出现的频率估计其概率,或者以抽样的数字特征估算随机变量的 数字特征,并将其作为问题的近似解。
1
4
的圆面积
=
(
圆内点数
/
总点数
)
∗
正方形面积
\color{red}{\frac{1}{4}的圆面积 = (圆内点数/总点数)*正方形面积}
41的圆面积=(圆内点数/总点数)∗正方形面积
2.3 应用1:计算不规则区域的面积
函数
e
x
2
e^{x^2}
ex2在区间
[
a
,
b
]
(
a
>
0
)
[a,b] (a>0)
[a,b](a>0)上的曲线如下图所示,计算曲线下与
x
x
x轴围成的阴影部分面积
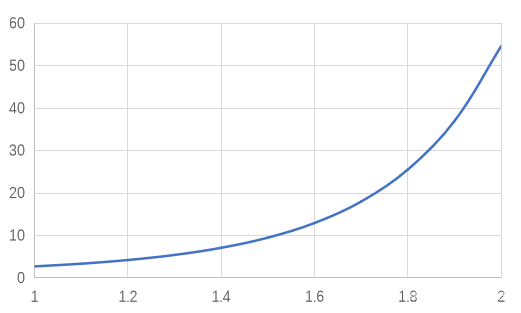
【思路】
- 在矩形区域 B = [ 1 , 2 ] × [ e a 2 , e b 2 ] B=[1,2]×[e^{a^2},e^{b^2}] B=[1,2]×[ea2,eb2]内随机采样 N N N个点;
- 计算落在阴影区域的点 (满足 0 < = y < = e x 2 0<=y<= e^{x^2} 0<=y<=ex2 ) 的数目(设为 M M M个);
- 阴影部分的面积为 M / N × a r e a ( B ) M/N×area(B) M/N×area(B)。
【练习1】求阴影部分的面积:
(
x
−
1
)
2
+
(
y
−
1
)
2
≤
1
x
2
+
y
2
>
2
2
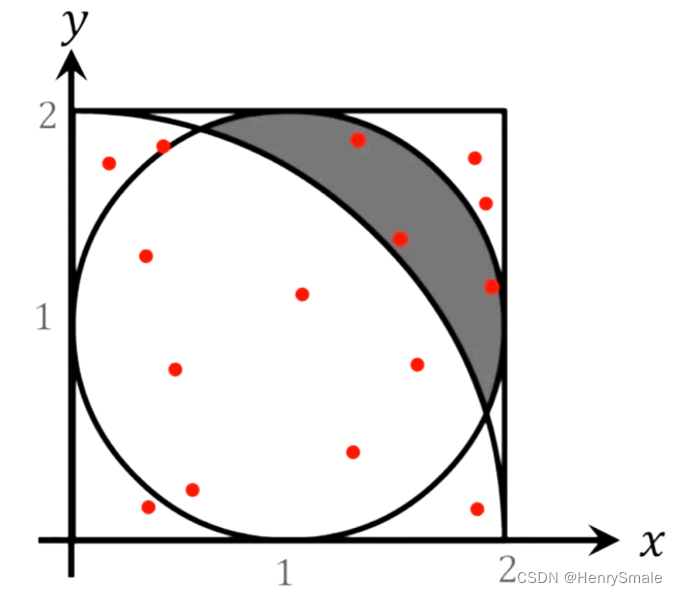
【练习2】计算不规则区域的体积
求坐标在原点的球
x
2
+
y
2
+
z
2
≤
4
x^2 + y^2 + z^2 \leq 4
x2+y2+z2≤4
与圆柱
(
x
−
1
)
2
+
y
2
≤
1
(x-1)^2 + y^2\leq 1
(x−1)2+y2≤1
的相交部分(称为Viviani体)的体积。

【分析】
在哪个区域采样?
如何判断采样点落在相交区域?
【思路1】相交区域内的点/球外切正方体内的点
import numpy as np
B = 2; N = 1000000;
M = 0
X = np.random.uniform(-B, B, size=N)
Y = np.random.uniform(-B, B, size=N)
Z = np.random.uniform(-B, B, size=N)
c1 = (X**2+Y**2+Z**2 < B**2) #bool类型的列表
c2 = ((X-1)**2+Y**2 <= (B/2)**2) #bool类型的列表
#c3 = np.int16(c1)+numpy.int16(c2)
#M = np.count_nonzero(c3==2)
c3 = c1 & c2 #与运算,得到一个bool类型的列表
M = np.sum(c3)
V = (2*B)**3
print(M/N*V)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
【思路2】相交区域内的点/球内点
from numpy import random
B = 2; N = 10000;
X = random.uniform(-B, B, size=N)
Y = random.uniform(-B, B, size=N)
Z = random.uniform(-B, B, size=N)
N_inS=0; N_inC=0
for i in range(N):
if X[i]**2 + Y[i]**2 + Z[i]**2 <= B**2:
N_inS += 1
if (X[i]-1)**2 + Y[i]**2 <= (B/2)**2:
N_inC += 1
V = 4*pi/3*(2**3)
print(N_inC/N_inS*V)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
2.4 应用2:蒙特卡洛积分
2.4.1 问题背景
对于区间[a,b]上的可积函数f,可以使用牛顿-莱布尼兹公式:
∫
a
b
f
(
x
)
d
x
=
F
(
x
)
∣
a
b
\int_{a}^{b} f(x) \mathrm{d} x=\left.F(x)\right|_{a} ^{b}
∫abf(x)dx=F(x)∣ab
其中
F
F
F是其原函数。
然而,某些情形下
F
(
x
)
F(x)
F(x)并不存在解析表达式,如当
f
(
x
)
=
x
x
f(x)=x^x
f(x)=xx ,
f
(
x
)
=
e
x
2
f(x)=e^{x^2}
f(x)=ex2,或者
f
(
x
)
=
sin
(
x
)
x
f(x)=\frac{\sin(x)}{x}
f(x)=xsin(x) 等。
可尝试使用蒙特卡洛方法近似计算定积分的值
2.4.2 蒙特卡洛积分
定积分:G是曲线
y
=
f
(
x
)
y=f(x)
y=f(x)与
x
x
x轴之间在
x
∈
[
a
,
b
]
x \in [a,b]
x∈[a,b]上的几何图形, 则G的面积值就是
∫
a
b
f
(
x
)
d
x
\int_{a}^{b} f(x) \mathrm{d} x
∫abf(x)dx, 设
B
=
[
a
,
b
]
×
[
0
,
m
]
B=[a,b]×[0,m]
B=[a,b]×[0,m], 则有
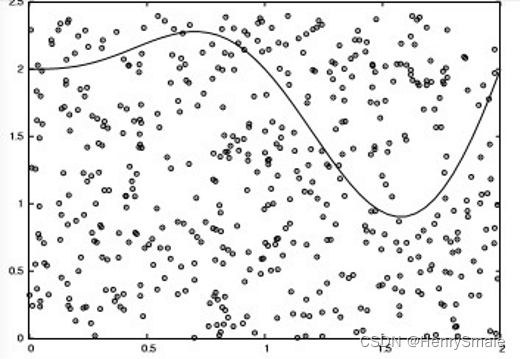
∫
a
b
f
(
x
)
d
x
≈
M
N
m
(
b
−
a
)
\int_{a}^{b} f(x) \mathrm{d} x \approx \frac{M}{N} m(b-a)
∫abf(x)dx≈NMm(b−a)
其中,
N
N
N为采样点数,
M
M
M为落在曲线与x轴之间区域的点的数目。
【例子1】
import numpy as np
def MCint_area(f, a, b, n, fmax):
below = 0
x = np.random.uniform(a, b, n)
y = np.random.uniform(0, fmax, n)
yCurve = f(x)
below = np.sum(y < yCurve)
area = below/n*(b-a)*fmax
return area
def f1(x):
return np.e**(x**2)
area = MCint_area(lambda x:np.e**(x**2), 1, 2, 100000, np.e**(2**2))
print(area)
area = MCint_area(f1, 1, 2, 100000, np.e**(2**2))
print(area)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
2.4.3 蒙特卡洛积分的误差

3 小结
- 随机函数
| 函数 | 范围 |
|---|---|
| import random | |
| r = random.random() | [0, 1) 实数 |
| r = random.uniform(a, b) | [a, b) 实数 |
| i = random.randint(a, b) | [a, b] 整数 |
| – | – |
| import numpy as np | |
| r = np.random.random(n) | [0, 1) n个实数 |
| r = np.random.uniform(a, b, n) | [a, b) n个实数 |
| i = np.random.randint(a, b+1, n) | [a, b] n个整数 |
| i = np.random.random_integers(a, b, n) | [a, b] n个整数 |
- 估算概率:做N次随机实验,某事件E发生的次数记为M.若极限 lim N → ∞ M N \lim_{N \rightarrow \infty} \frac{M}{N} limN→∞NM存在,则称该极限为事件E发生的概率. 一般情况下,可以用N取较大值时 M N \frac{M}{N} NM的值来近似替代这个概率值.
- 蒙特卡洛方法:
– 基本思想:大量随机采样
– 典型应用:计算不规则区域的面积/体积;求数值积分。
4 课后延伸
- 将上面的所有程序抄写一遍;
- 调研蒙特卡洛方法在机器学习上的论文,阅读一篇后撰写读书笔记。
附录 Numpy运算
逻辑运算
np.logical_and([True, False], [False, False]) &
np.logical_or([True, False], [False, False]) |
np.logical_not([True, False])
- 1
- 2
- 3
比较运算
np.greater([4,2],[2,2])
np.greater_equal([4, 2], [2, 2])
np.less([1, 2], [2, 2])
np.less_equal([4, 2, 1], [2, 2, 2])
np.equal([1.,2], [1., 3])
np.not_equal([1.,2], [1., 3])
- 1
- 2
- 3
- 4
- 5
- 6


