- 1Ubuntu22.04安装Nvidia 550驱动和CUDA toolkit 12.4.1
- 2Mac app文件签名与公证_xcrun notarytool store-credentials
- 3Kafka的概念详解_kafka topic
- 4笔记神器: Gitee+Typora+Git Bash (全部免费)
- 5c语言-链表创建-合并-删除等复试常见操作_#include
#include typedef struc - 6程序员的出路是什么?
- 7数据结构 数组、链表_数组链表
- 8Verilog时钟分频(偶数分频、奇数分频、小数分频、半整数分频)
- 9用python实现堆_python 堆怎么写
- 10蓝桥杯真题【递增序列】_递增序列蓝桥杯
DP模型——区间DP_dp模型的流应力比
赞
踩
前言
在区间范围内做DP
能使用区间DP重要的一点在于,能把所求的问题划分成两个独立的问题和可能已知的某一个最小问题,最后三个问题加起来就是答案
环形DP转线性
环形石子合并
方法一
我们最后要求的是在环形中将相邻的两堆石子来合并,即我们现有的两个相邻的石子来连边,最后会连成分成了两堆石子,再练一条边,最后一定会用到n-1条边,那么最后一定会有某两个相邻点是没有连边的,是有一个缺口的,那么我们可以枚举这个缺口来进行操作。然后把剩下的拉成一个链即可。
最后的复杂度是 N ∗ N 3 N*N^3 N∗N3(N是枚举缺口,N3是条形石子合并的时间复杂度)
方法二
基于上面的方法,我们本质上是求n个长度为n的链上的石子合并问题
那么我们可以有一种常用的优化方法:把这条链再复制一遍接到原来的尾上,那么最后我们对这个链上长度为n的区间再进行操作就包含了上面的所有的n个长度为n的链
例:1 2 3 4变成1 2 3 4 1 2 3 4
Code
// Problem: 环形石子合并 // Contest: AcWing // URL: https://www.acwing.com/problem/content/1070/ // Memory Limit: 64 MB // Time Limit: 1000 ms // Code by: ING__ // // Edited on 2021-08-10 16:50:06 #include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #include <map> #include <vector> #include <set> #include <queue> #include <stack> #include <sstream> #define ll long long #define re return #define Endl "\n" #define endl "\n" using namespace std; const int N = 410; int n; int a[N]; int s[N]; int f[N][N]; int main(){ cin >> n; for(int i = 1; i <= n; i++){ cin >> a[i]; a[i + n] = a[i]; } for(int i = 1; i <= 2 * n; i++){ s[i] = s[i - 1] + a[i]; } int ans = 1e8; for(int len = 2; len <= n; len++){ // min for(int i = 1; i <= 2 * n - len + 1; i++){ int l = i; int r = i + len - 1; f[l][r] = 1e8; for(int k = l; k < r; k++){ f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]); } } } for(int i = 1; i <= n; i++){ ans = min(ans, f[i][i + n - 1]); } cout << ans << endl; ans = 0; memset(f, 0, sizeof(f)); for(int len = 2; len <= n; len++){ // max for(int i = 1; i <= 2 * n - len + 1; i++){ int l = i; int r = i + len - 1; // f[l][r] = -1e8; for(int k = l; k < r; k++){ f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]); } } } for(int i = 1; i <= n; i++){ ans = max(ans, f[i][i + n - 1]); } cout << ans << endl; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
能量项链
两颗相连的珠子(a, b)和(b, c)释放的能量为a*b*c,合并后为(a, c)。将这N颗珠子合并为一个珠子的方案中,释放的总能量最大是多少
状态表示
f[l, r]表示所有将[l, r]合并在成一个珠子的方式的值
状态计算
从最后一步来划分,就是从L到K合并K到R区间的产生的价值
f
[
L
,
R
]
=
m
a
x
(
f
[
L
,
R
]
,
f
[
L
,
K
]
+
f
[
K
,
R
]
+
w
[
L
]
∗
w
[
K
]
∗
w
[
R
]
)
f[L,R]=max(f[L,R],f[L,K] + f[K,R]+w[L]*w[K]*w[R])
f[L,R]=max(f[L,R],f[L,K]+f[K,R]+w[L]∗w[K]∗w[R])
Code
// Problem: 能量项链 // Contest: AcWing // URL: https://www.acwing.com/problem/content/322/ // Memory Limit: 64 MB // Time Limit: 1000 ms // Code by: ING__ // // Edited on 2021-08-11 09:49:25 #include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #include <map> #include <vector> #include <set> #include <queue> #include <stack> #include <sstream> #define ll long long #define re return #define Endl "\n" #define endl "\n" using namespace std; typedef pair<int, int> PII; int dx[4] = {-1,0,1,0}; int dy[4] = {0,1,0,-1}; int n; int a[210]; int f[210][210]; int main(){ cin >> n; for(int i = 1; i <= n; i++){ cin >> a[i]; } for(int i = 1; i <= 2 * n; i++){ a[i + n] = a[i]; } for(int len = 3; len <= n + 1; len++){ for(int i = 1; i <= 2 * n - len + 1; i++){ int l = i; int r = i + len - 1; // f[l][r] = for(int k = l + 1; k < r; k++){ f[l][r] = max(f[l][r], f[l][k] + f[k][r] + (a[l] * a[k] * a[r])); } } } int ans = 0; for(int i = 1; i <= 2 * n; i++){ ans = max(ans, f[i][i + n]); } cout << ans << endl; return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
记录方案数
区间DP+高精度
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
状态分析
(不是我想的,太秒了)
我们固定好一个边,就确定了两个点,那么再连一个点就构成一个三角形

那么这个三角形就把一个多边形分成了左边一个多边形,中间一个三角形,右边一个三角形;因为其三角形不能相交,所有左右两边的多边形一定是独立的划分
然后在确定的其中的一个多边形内,在多边形内的这个区间内,分成若干个三角形
集合就是:所有将从L到R之间构成的N-2个互不相交的三角形的方法的集合
状态计算
f [ L , R ] = m i n ( f [ L , R ] , f [ L , K ] + f [ K , R ] + w [ L ] ∗ w [ K ] ∗ w [ R ] ) f[L,R]=min(f[L,R],f[L,K] + f[K,R]+w[L]*w[K]*w[R]) f[L,R]=min(f[L,R],f[L,K]+f[K,R]+w[L]∗w[K]∗w[R])
这题三个数撑起来爆ll了需要用高精度,偷懒直接写py了
Code
# // Problem: 凸多边形的划分 # // Contest: AcWing # // URL: https://www.acwing.com/problem/content/1071/ # // Memory Limit: 64 MB # // Time Limit: 1000 ms # // Code by: ING__ # // # // Edited on 2021-08-11 10:50:32 n = int(input()) a = [0 for i in range(55)] f = [] for i in range(55): f.append([0] * 55) _ = input().split() for i in range(0, n): a[i + 1] = int(_[i]) for len in range(3, n + 1): for i in range(1, n - len + 2): l = i r = i + len - 1 f[l][r] = 1e38 for k in range(l + 1, r): # 长度为1的多边形没有意义 f[l][r] = min(f[l][r], f[l][k] + f[k][r] + a[l] * a[r] * a[k]) print(f[1][n])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
二维区间DP
状态表示
f[x1, y1, x2, y2, k]表示将子矩阵(x1, y1)(x2, y2)切成k部分的所有方案
属性
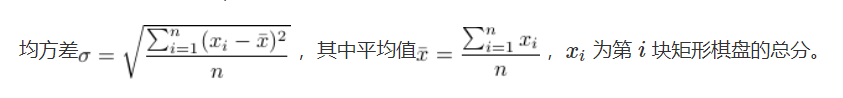
的最小值
状态计算
我们把最后一步的状态分为横着切的和竖着切的
那么就可以这样分:
横着切:
在这个区间内枚举所有最后一步是横着切的得到的棋盘
竖着切:
在这个区间内枚举所有最后一步是横着切得到的棋盘
对上面切的得到的两个棋盘,其中一个需要继续操作
还有均方差公式,高中的时候有一个公式就是xi的平方的平均数减去xi平均数的平方
Code
// Problem: 棋盘分割 // Contest: AcWing // URL: https://www.acwing.com/problem/content/323/ // Memory Limit: 10 MB // Time Limit: 1000 ms // Code by: ING__ // // Edited on 2021-08-11 15:08:57 #include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #include <map> #include <vector> #include <set> #include <queue> #include <stack> #include <sstream> #define ll long long #define re return #define Endl "\n" #define endl "\n" using namespace std; typedef pair<int, int> PII; const int m = 8; const int N = 15, M = 9; int n; int s[M][M]; double f[M][M][M][M][N]; double xba; double get(int x1, int Y1, int x2, int y2){ // 算均方差的平方 double summ = s[x2][y2] - s[x1 - 1][y2] - s[x2][Y1 - 1] + s[x1 - 1][Y1 - 1] - xba; return summ * summ / n; } double dp(int x1, int Y1, int x2, int y2, int k){ double &v = f[x1][Y1][x2][y2][k]; if(v >= 0) return v; if(k == 1) return v = get(x1, Y1, x2, y2); v = 1e9; for(int i = x1; i < x2; i++){ v = min(v, get(x1, Y1, i, y2) + dp(i + 1, Y1, x2, y2, k - 1)); v = min(v, get(i + 1, Y1, x2, y2) + dp(x1, Y1, i, y2, k - 1)); } for(int i = Y1; i < y2; i++){ v = min(v, get(x1, Y1, x2, i) + dp(x1, i + 1, x2, y2, k - 1)); v = min(v, get(x1, i + 1, x2, y2) + dp(x1, Y1, x2, i, k - 1)); } return v; } int main(){ cin >> n; for(int i = 1; i <= m; i++){ for(int j = 1; j <= m; j++){ cin >> s[i][j]; s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; } } memset(f, -1, sizeof(f)); xba = (double)s[m][m] / n; printf("%.3lf", sqrt(dp(1, 1, 8, 8, n))); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78




