图的遍历 深度优先遍历(爱思创)_给定一个无向图,输出指定顶点出发的深度优先遍历序列。在深度优先遍历的过程中,如

前言:

这篇文章还是是为了帮助一些

像我这样的菜鸟

找到简单的题解

问题描述:

输入格式

输出格式

8
0 1 1 0 0 0 0 0
1 0 0 1 1 0 0 0
1 0 0 0 0 0 1 1
0 1 0 0 0 1 0 0
0 1 0 0 0 1 0 0
0 0 0 1 1 0 0 0
0 0 1 0 0 0 0 1
0 0 1 0 0 0 1 0

1-2-4-6-5-3-7-8

问题提示

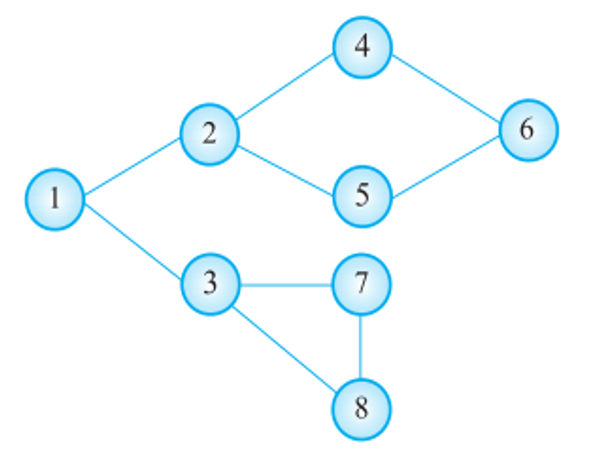
问题解析:

图DFS另外一种输入方法

第一种是读入每条边

图的遍历 DFS遍历(深学思维)_吾乃狙击神蛐的博客-CSDN博客

代码部分:

变量部分

const int N=105;//数组大小
int a[N][N];
bool vis[N];//标记
int n;

然后是DFS部分

void dfs(int step)
{
	if(step>n)
	{
		return;
	}
	for(int i=1;i<=n;i++)
	{
		if(a[step][i]==0) continue;//如果空不访问
		if(vis[i]) continue;//如果走过不访问
		cout<<"-"<<i;//输出答案
		vis[i]=1;//标记本格
		dfs(i);//递归调用DFS
	}
	return;
}

最后是主函数部分

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];//输入答案
		}
	}
	vis[1]=1;
	cout<<1;//输出起点
	dfs(1);//从起点遍历
	return 0;
}

完整代码:

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int a[N][N];
bool vis[N];
int n;
void dfs(int step)
{
	if(step>n)
	{
		return;
	}
	for(int i=1;i<=n;i++)
	{
		if(a[step][i]==0) continue;
		if(vis[i]) continue;
		cout<<"-"<<i;
		vis[i]=1;
		dfs(i);
	}
	return;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}
	}
	vis[1]=1;
	cout<<1;
	dfs(1);
	return 0;
}

AC