电磁学2——电磁场与电磁波：麦克斯韦方程组_麦克斯韦方程组csdn

前言1：数学场论基础知识

一、电磁场

1.1、常见考试范围

课本例题、课后习题、找试卷

代数基础

求点积（散度）、叉积（旋度）、梯度
散度定理
旋度定理

毕萨定律、安培环路定律

麦克斯韦方程组、三个结构方程、复数形式

证明基尔霍夫电压定律、基尔霍夫电流定律

能量守恒： 坡印廷矢量、坡印廷定理

两种特殊情况的边界条件

理想的介质和理想的导体
电力不躺、电躺不力的物理意义

静电场边值问题：镜像法、虚拟电荷

理解介质的平面波：真空、波长、相速

1.2、基础公式

1.2.1静电场库伦定律

求空间某一点的电场方向和大小（静电荷引发的电场）

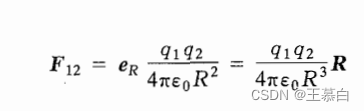
1.2.2 稳恒磁场毕萨定律

稳恒磁场：即导线通电之后的磁场
求空间某一点的磁感应强度方向和大小（电流激发的磁场）

毕萨定律的应用
无限长载流直导线
载流圆线圈中心
无限长螺线管

1.2.3 静电场的高斯定理（简化版描述电）

真空中的静电场中，穿过任意闭合曲面的电通量与该曲面所包围的电荷电量和真空介电常数有关：
1.电通量$\varphi =E对S的面积分$
2.场强E是所有电荷产生的，电通量$\varphi$只与内部电荷有关
3.点电荷位于闭合面外，穿入必定传出，即面不包含源时电通量为0
4.因为存在场源电荷，故静电场是有源场

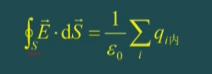
1.2.4 稳恒磁场高斯定理（简化版描述磁）

恒定电流磁场是稳恒磁场
稳恒磁场中，穿过任意闭合曲面S的总磁通量必然为0：
磁通量$\varphi =B对S面积分$

1.2.5 静电场安培环路定理（简化版磁生电）

静电场中，沿着闭合路径的环路积分为0：
1.点电荷对一个感应电荷沿着曲线所做的功只取决于始末位置，与路径无关
故静电力是保守力，静电场是保守场
2.静电场环流量=0，故静电场是无旋场，有旋场环路积分不为0
静电场的电场线不能闭合
3.$电势差=E对路径的积分$、$做功=电荷量\ast 电势差$

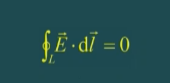
1.2.6 稳恒磁场安培环路定理（简化版电生磁）

1.3、麦克斯韦方程组

1.3.1 描述电（静电场高斯定理）

——电场强度在闭合曲面上的通量=内部电荷数/介电常数，即离开物体的电场线数目只与内部电荷数有关

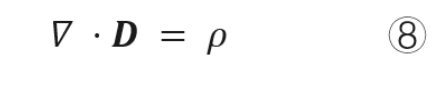
1.3.2 描述磁（稳恒磁场高斯定理、磁通连续性原理）

——磁感应强度在闭合曲面上通量为0

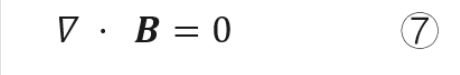
1.3.3 磁生电（法拉第定律）

电场在线上的环流量，即电势=磁场变化率（非闭合面的磁通量对时间求导数）
相关理论：
静电场安培环路定理（只是发现环路积分为0）
法拉第电磁感应定律：运动、变化的磁场产生电场（无公式）

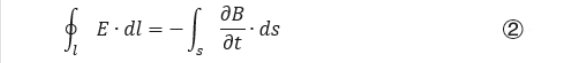
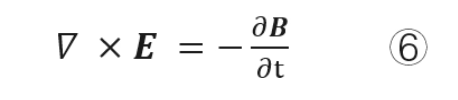
1.3.4 电生磁(全电流定律，麦克斯韦-安培定律)

磁场在线上的环流量=电流+电场变化率

相关理论：
奥斯特发现电流旁边小磁针偏转,电流旁边有磁场
安培：两根导线、螺线管实验
稳恒磁场安培环路定理：u0I内、电流产生稳恒磁场

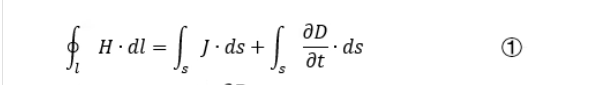
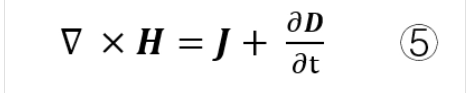
1.3.5电流连续性方程（电荷守恒定律）

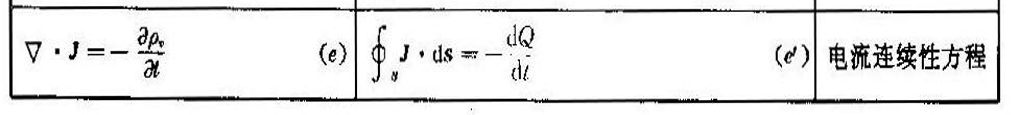
1.3.6对麦克斯韦方程组的思考？

由麦克斯韦方程组得到产生磁场的原因：
恒定电流产生稳恒磁场即静磁场
变化的电流会产生变化的磁场
变化的电场会产生变化的磁场
静磁场不会产生电场，变化的磁场会产生变化的电场

电荷变化电场
运动电荷即电流产生磁场
变化的电场产生磁场
变化的磁场变化电场

二、介质与电磁波

2.1、本构关系

由库仑定律和毕萨定律：
D、H只与源有关，去除介质的影响了
E、B与介质和源都有关系
实际电场强度E与介质参数介电常数负相关
实际磁场强度B与介质的参数磁导率正相关

公式1：D=$\epsilon$E

电位移矢量、电通量密度、电感应强度D（单位:库伦C/m2）
——从单位上看D只与源有关，去除介质的影响了
——因为对面积的积分是库伦，所以叫做电通密度

电场强度E（矢量,单位:V/m、N/C库伦）
——描述电场的强度和方向，影响静止电荷所受力的大小
——电场线疏密描述电场的强弱

实际介电常数$\epsilon$（单位:法拉F/m）
真空介电常数${\epsilon }_0=\frac{1}{36\pi }\ast 10^{-9}$（单位:法拉F/m、C/(V*m)）

公式2： B=uH

磁感应强度、磁通量密度B（单位：T特斯拉）
——描述磁场的强度和方向，影响运动电荷所受力的大小
——右手螺旋描述磁感应强度方向，左手大拇指受力方向

磁场强度H（单位：A/m）
——从单位上看H只与源有关，去除介质的影响了

磁导率$u$（单位：亨H/m）
真空磁导率$u_0=4\pi \ast 10^{-7}$（单位：亨H/m）

公式3：J=$\sigma$E

电导率$\sigma$（单位：西门子S/m）
电场强度E（矢量,单位：V/m、N/C库伦）

电流密度J（矢量，描述移动电荷）
——单位时间内垂直通过电流传播方向的电量，用来帮助选择导线，越大越厉害但更危险
体电流密度$J_v$（矢量,单位：$A/m^2$）
——单位时间通过导体单位面积的电荷量
面电流密度$J_s$（矢量,单位：A/m）
——电荷在面上移动，单位时间通过导体单位长度截线的电荷量
线电流密度即电流$I$（标量,单位：A，C/s）
——单位时间通过导体某个横截面的电荷量，好比水流的大小

电荷密度$\rho$(标量，描述某一时刻电荷)
体电荷密度(${\rho }_v$，标量，单位：$C/m^3$)
——单位体积上电荷量，均匀带电球体有体电荷密度参数
面电荷密度(${\rho }_s$，标量，单位：$C/m^2$)
——单位面积上电荷量的多少
线电荷密度(${\rho }_l$，标量，单位：$C/m$)
——单位长度上电荷量的多少

关键点：把导线的截面看做什么东西
通过截面S的电流$I=\int J_{v}dS$(标量,单位:A)
体电荷量$Q=\int {\rho }_{v}dv=\int Idt$ (标量,单位:C)
通过截线的电流$I=\int J_{s}dl$(标量,单位:A)
面电荷量$Q=\int {\rho }_{s}ds=\int Idt$ (标量,单位:C)
通过横截面的电流$I$(标量,单位:A)
面电荷量$Q=\int {\rho }_{l}dl=\int Idt$ (标量,单位:C)

2.2、介质参数$\epsilon 、u、\sigma$详解

1.介电常数（电容率）$\epsilon$

——读法：爱不色龙(permittivity、dielectric constant、DK)
——描述空间与物质对电场的抵抗能力，电介质介电常数$\epsilon >$真空介电常数${\epsilon }_0$
——例1：电场，介质在外加电场时会产生感应电荷而削弱电场，原外加电场(真空中)与最终介质中电场比值即为介电常数,又称诱电率。静电场中电介质介电常数越大，介质内部反抗外加电场的能力越强，电介质中最终电场强度越小。
——例2：电容，因为介电常数可以反映在电场作用下电容中填充的电介质（绝缘体）的电荷不动的能力。电容中的介电常数越大说明绝缘性强以及介质对自己电子的束缚能力越好，增加相对介电常数来增加电容容量。
——例3：极性，根据物质的介电常数可以判别高分子材料的极性大小。通常，相对介电常数大于3.6的物质为极性物质；相对介电常数在2.8~3.6范围内的物质为弱极性物质；相对介电常数小于2.8为非极性物质。

2.复介电常数Dk与介电损耗因子Df

复介电常数Dk

介电损耗因子Df (损耗角正切loss tangent)

Lossy material 有耗介质

3.电导率（电阻率的倒数）$\sigma$

——读法：c个码(conductivity、specific conductance、EC)
——描述在电场作用下不同导体介质的电荷移动的能力，越大说明阻性越弱
——例：J=$\sigma$E说明在一个电压源的作用下形成导体电流，微观上导电媒介和外加的电场一起影响电流密度，宏观上即电阻和外加带电压一起影响导体中的电流。$铜是10^6，水是10^{-7}$

4.磁导率（电感率）$u$与 磁化率$x$

——读法：谬(permeability、magnetic conductivity)
——描述导通磁场的能力，顺磁、抗磁、铁磁介质的磁导率$u$相对于$u_0$有大有小
——例1：稳恒磁场磁介质磁导率越大则磁感应强度越强
——例2：磁导率可以反映在空间或在磁芯空间中的线圈流过电流后，磁介质导通(小于真空磁导率即阻碍)磁场传播的能力

2.3、不同的介质中波的反射、传播特性

注解：J、E是矢量
注解：媒介表面电场垂直分量$E_n$和平行分量$E_t$

1.理想介质

$\sigma =0$，即理想介质是无耗介质(没有热损耗)
$自由电荷\rho =0,传导电流J=0$，即理想介质是无源介质

电磁波在真空中速率固定，速度为光速c=$\frac{1}{\sqrt[]{u_0{\epsilon }_0}}$（m/s）
电磁波在各种介质中的传播速度（m/s）
$v=\frac{c}{n}=\frac{1}{\sqrt[]{u\epsilon }}=\frac{c}{\sqrt[]{u_r{\epsilon }_r}}=\frac{\lambda }{T}=\lambda f=\frac{w}{k}$
——当波速确定时，不同频率的电磁波的波长也确定下来
注：
n是介质的折射率=$\frac{入射角正弦}{反射角正弦}$
w角频率=$\frac{2\pi }{T}$
k相位常数（波数）=$\frac{2\pi }{\lambda }$
角频率与相位常数作用：反映了单位时间或单位长度有多少个$2\pi$

波阻抗、本征阻抗、特征阻抗：反映的是电磁场振幅即最大的幅值之间的关系
$\eta$=$\frac{电场振幅}{磁场振幅}$=$\sqrt{\frac{u}{\epsilon }}$=${\eta }_0\sqrt{\frac{u_r}{{\epsilon }_r}}$
在自由空间中，均匀平面波的本征阻抗为${\eta }_0=\sqrt{\frac{u_0}{{\epsilon }_0}}$=120π≈377(Ω)。

2.导电媒介

$\sigma$有限，即导电媒介是有耗介质
${\rho }_v=0$，即导电媒介没有电荷源
$J_v\ne 0、E_t\ne 0$，即导电媒介有电流源

弱导电媒介（良介质）:$\sigma$很小，损耗角正切$\frac{\sigma }{w\epsilon }<<1$
良导体:$\sigma$很大，损耗角正切$\frac{\sigma }{w\epsilon }>>1$

通电同轴电缆表面：
导体外表面$E=E_{\rho }+E_z$
导体外表面的能量流动$S_{av1}=E_{\rho }\times H_{\varphi }$
导体外表面进入导体的能量，即能量损耗$S_{av2}=E_z\times H_{\varphi }$
1.电场强度切向必定连续
若电场强度有切向分量E_z，$E_z=E_{内z}=J/\sigma$
注:这里的J是内表面位置的电流密度

下面的都不清楚？？？？
2.电场强度有法向电场分量(电通密度的法向分量等于电荷密度)，则有电荷，$n\cdot (E_{\rho }-E_{内\rho })={\rho }_s\ne 0$
3.磁感应强度没有法向分量(电场强度法向必定连续，为0)
4.若磁感应强度有切向磁场分量(磁场强度的切向分量等于电流密度)，则有电流，$n\times H_{\varphi }=J\ne 0$

3.理想导体

$\epsilon 、\sigma =\infty$
——理想导体的定义
${\rho }_v=0$、$J_v=0$
——内部没有自由电荷、没有体电流密度，内部电场、磁场强度均为0
注：理想导体不用来传电磁波，电磁波会在导体表面全反射

理想导体表面：
1.电场强度切向必定连续
——内部电场为0，故电场强度没有切向分量
2.电通密度的法向分量之差等于电荷密度
——若电场强度有法向电场分量，则有表面电荷，$n\cdot D=D_n={\rho }_s\ne 0$
3.电场强度法向必定连续
——内部电场为0，磁感应强度没有法向分量
4.磁场强度的切向分量之差等于电流密度
若磁感应强度有切向磁场分量，则有表面电流，$n\times H=H_t=J_s\ne 0$注：此时的电流密度与切向电场无关

2.4 一些常见问题理解

光与电磁波有哪些性质？

透射、反射、绕射(衍射)
干涉与驻波，驻波必须在同一条直线上
偏振与极化

2.4G和5G的区别？介电常数和介电损耗对透射波和透射波的传播的影响

1、2.4G传播距离更远的原因？
解释：就像在导电媒介中，频率越低衰减常数越小，衰减越慢，所以传播距离远

2、有障碍物时，2.4G的信息传输速率更快，2.4G的穿墙能力更强，这个穿墙效果是绕射(衍射)与透射的效果叠加。但如何衡量透射能力？是初始值还是透过去的数值？
1.绕射波：绕射由波长和障碍物尺寸决定，一般认为2.4G的绕射能力更强
波长越长（大于障碍物尺寸），波动性越明显，越容易发生衍射现象
举例：小孔成像

2.表面的透射波大小：查介质材料的损耗系数图，
相同介质，频率越高损耗系数越大，表面的透射波越小反射波越大
相同频率下，介质损耗角正切越大，透射波越小
注：需要研究不同材料特性阻抗，计算反射系数和回波损耗

3.透射波的传播：查介质材料的衰减系数图
相同介质，频率越高衰减系数越大，也是5G传播不远的原因
相同频率下，介质损耗角正切越大，衰减越快
注：X射线透射能力强又是另外的物理原因

媒介的线性，均匀，各向同性？

线性：介电常数不随电场变化
均匀：介质在一定范围内是均匀的，而不是一些地方疏、一些地方密
各向同性：各个方向上的传播特性相同

理想介质、真空、空气区别？

理想介质：电导率为0，介电常数不一定
真空：没有介质，但电导率为0，介电常数为1(即真空介电常数)
电磁波传播不需要介质，在真空在传递电磁波时可以看做是在介电常数为1的理想介质中传播吗？
空气：电导率接近0，介电常数近似1，可以看做理想介质吗？

导体表面与波导表面的电流是如何形成的?坡印廷如何传递能量？

内表面还是外表面

三、从麦克斯韦方程到均匀平面波

E(r,t)是含有空间和时间变量的电场强度矢量场或矢量函数
空间中的每个点都像场源一样向着任意方向发射电磁波
电场强度和磁场强度在电磁场传播方向上没有分量，只有x和y的分量，并且x与y的分量至于z有关

时谐电磁场频域分析
亥姆霍兹方程
达朗贝尔方程

平面电磁波等相位面方程可以推相速就是光速
——波的等相位面又叫波阵面
——标量等值面、天线场的等相位面

振幅：即点能达到的最大位置
行波：同一时刻不同位置的点相位不同，与自己的位置有关，所有点的振幅相同
驻波：同一时刻不同位置的点相位相同，每个位置的点振幅不同
TEM波：电场分量和磁场分量相互垂直，且都垂直于传播方向的电磁波
TE波指电矢量与入射面垂直，或者说传播方向上没有电矢量有磁矢量（横电波）
TM波是指磁矢量与入射面垂直，而电场矢量在传播方向上有分量（横磁波）