机器学习-数据归一化方法（Normalization Method）1._归一化可学系参数 正确的表达式是

https://blog.csdn.net/program_developer/article/details/78637711
出现背景：

从左至右来看，第一个模型是一个线性模型，拟合度很低，也称作欠拟合（Underfitting），不能很好地适应我们的训练集；第三个模型是一个高次方的模型，属于过度拟合，虽然能很好的适应我们的训练数据集，但是在新输入变量进行预测的时候，可能效果会很差。第二个模型可能是刚刚适合我们数据的模型。
那么问题来了，如果我们发现这样过度拟合的情况，如何处理呢？
有两种方式：
1.丢弃一些不能帮助我们正确预测的特征。采用的方法如下：

     手工选择保留哪些特征。
    使用一些模型选择算法来帮忙降维。（例如PCA等）

2.归一化处理

     保留所有的特征，但是减少参数的大小（或者是说：减少参数的重要性）

定义：
不同的评价指标往往具有不同的量纲（例如：对于评价房价来说量纲指：面积、房价数、楼层等；对于预测某个人患病率来说量纲指：身高、体重等。）和量纲单位（例如：面积单位：平方米、平方厘米等；身高：米、厘米等），这样的情况会影响到数据分析的结果，为了消除指标之间量纲的影响，需要进行数据标准化处理，已解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。
优点：
（1）归一化后加快了梯度下降求最优解的速度。
（2）归一化有可能提高精度（归一化是让不同维度之间的特征在数值上有一定的比较性）。
解释（1）加快梯度下降求最优解的速度：
例子：假定为了预测房子价格，自变量为面积，房间数两个，因变量为房价。
那么可以得到的公式为：

首先我们给出两张图代表数据是否均一化的最优解寻解过程。

未归一化：

归一化之后：

我们在寻找最优解的过程中也就是在使得损失函数值最小的theta1、theta2。上述两幅图代表的是损失函数的等高线。我们很容易看出，当数据没有归一化的时候，面积数的范围可以从0-1000，房间数的范围一般为0-10，可以看出面积数的取值范围远大于房间数。
归一化和没有归一化的影响：
这样造成的影响就是在形成损失函数的时候：
数据没有归一化的表达试可以为：

造成图像的等高线为类似的椭圆形状，最优解的寻优过程如下图所示：

而数据归一化后，损失函数的表达式可以表示为：

其中变量的前面系数都在【0-1】范围之间，则图像的等高线为类似的圆形形状，最优解的寻优过程如下图所示:

从上面可以看出，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解。

解释：（2）归一化有可能提高精度（归一化是让不同维度之间的特征在数值上有一定的比较性）。

一些分类器需要计算样本之间的距离（如欧式距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况不符。（比如，这时实际情况是值域范围小的特征更重要）。
两种常用的归一化方法：
（1）min-max标准化
（2）Z-score标准化方法
min-max标准化（Min-Max Normalization）（线性函数归一化）

    定义：也称为离差标准化，是对原始数据的线性变换，使得结果映射到0-1之间。
    本质：把数变为【0,1】之间的小数。
    转换函数：（X-Min）/(Max-Min)
    如果想要将数据映射到-1,1，则将公式换成：（X-Mean）/(Max-Min)

其中：max为样本数据的最大值，min为样本数据的最小值，Mean表示数据的均值。
缺陷：当有新数据加入时，可导致max和min的变化，需要重新定义。
0均值标准化（Z-score standardization）

    定义：这种方法给与原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1.
    本质：把有量纲表达式变成无量纲表达式。
    转换函数：（X-Mean）/(Standard deviation)

其中，Mean为所有样本数据的均值。Standard deviation为所有样本数据的标准差。
两种归一化方法的使用场景：
（1）在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。
因为：第一种方法(线性变换后)，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。
（2）在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在0 255的范围。
因为：第二种归一化方式中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。

为什么在距离度量计算相似性、PCA中使用第二种方法(Z-score standardization)会更好呢？我们进行了以下的推导分析：

归一化方法对方差、协方差的影响：假设我们数据为2个维度（X、Y）,首先看均值为0对方差、协方差的影响：
我们使用Z-score标准化进行计算，我们先不做方差归一化，只做0均值化为:

新数据的协方差为：

由于

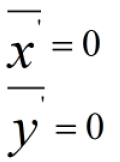
因此：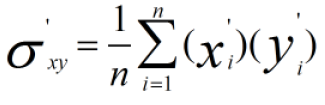

而原始数据协方差为：

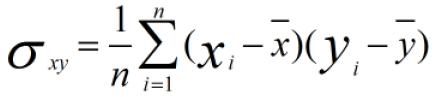
因此：

做方差归一化后：
                 

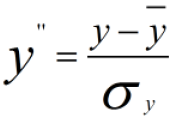
方差归一化后的协方差为：

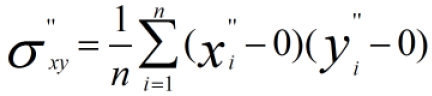
使用Min-Max标准化方法进行计算，为了方便分析，我们只对X维进行线性函数变换

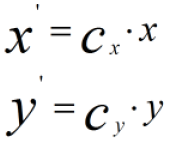
计算协方差：

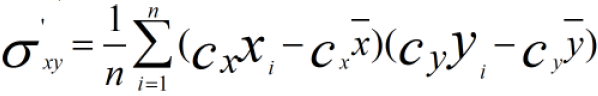
总结：
使用Max-Min标准化后，其协方差产生了倍数值得缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时由于量纲的存在，使用不同的量纲，距离的计算结果会不同。
在Z-score标准化（0均值标准化）中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0,、方差为1的正态分布，在计算距离的时候，每个维度 都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。
总的来说，在算法、后续计算中，涉及距离度量（聚类分析）或者协方差分析（PCA、LDA等）的，同时数据分布可以近似为状态分布，应当使用0均值化的归一方法。其它应用中，根据具体情况选用合适的归一化方法。

参考文献：http://blog.csdn.net/yehui_qy/article/details/53787386
                http://blog.csdn.net/zbc1090549839/article/details/44103801
               知乎：处理数据时不进行归一化会有什么影响？归一化的作用是什么？什么时候需要归一化？有哪些归一化的方法？ - 忆臻的回答 - 知乎
               https://www.zhihu.com/question/20455227/answer/197897298
               http://blog.csdn.net/mysteryhaohao/article/details/51261300
---------------------  
作者：Microstrong0305  
来源：CSDN  
原文：https://blog.csdn.net/program_developer/article/details/78637711  
版权声明：本文为博主原创文章，转载请附上博文链接！