数据结构之堆_堆分为大根堆和小跟堆

堆

简单介绍：

堆是利用完全二叉树的结构来维护一组数据，然后进行相关操作，一般的操作进行一次的时间复杂度在 $O(1)$ ~ $O(logn)$ 之间。

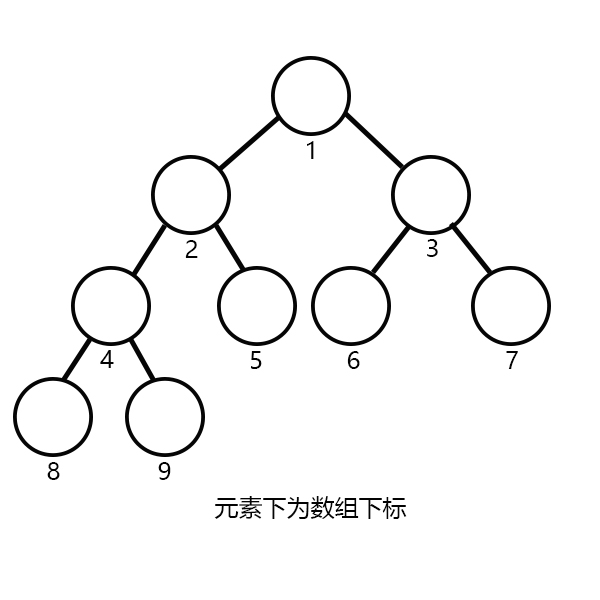
完全二叉树：若设二叉树的深度为 h，除第 h 层外，其它各层 ( 1～ h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

如图所示为一棵完全二叉树：

堆分为两种类型：大根堆、小根堆

顾名思义，就是保证根节点是所有数据中最大/小。

堆的存储：一个一维数组，节点编号从 1 开始，左儿子的编号 2x 、右儿子的编号 2x + 1 。

up 操作：

模拟：在堆中分别加入：{8，5，2，10，3，7，1，4，6}。如图所示：

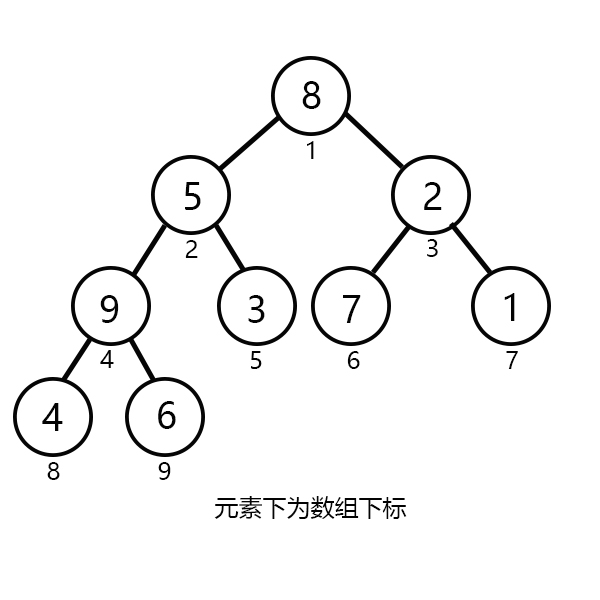
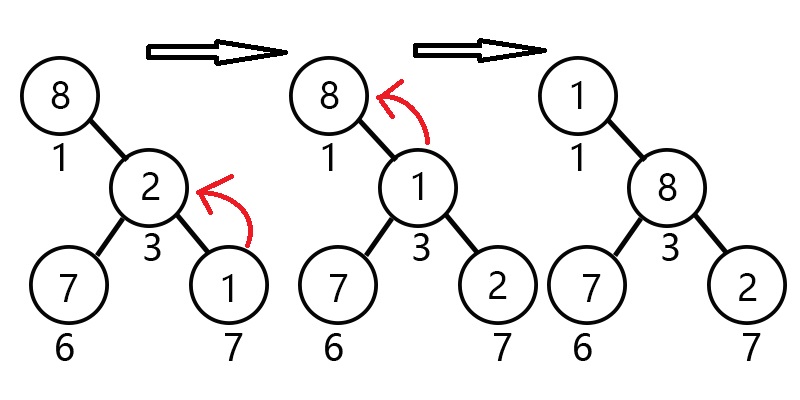
​ 以小根堆为例：从上面的数据中可以看出，根节点 1 元素 8 绝对不是最小的。我们很容易发现它的一个儿子节点 3 (元素 2 )比它来的小，我们怎么将它放到最高点呢？很简单，可以直接交换！但是，我们又发现了，3 的一个儿子节点 7 (元素 1 )似乎更适合在根节点。这时候我们是无法直接和根节点交换的，那我们就需要一个操作来实现这个交换过程，那就是 up 操作。从下往上找比自己大的数，然后递归交换。

操作过程如下：

从当前结点开始，和它的父亲节点比较，若是比父亲节点来的小，就交换，然后将当前询问的节点下标更新为原父亲节点下标；否则退出。

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2]) 
    {
    	swap(h[u], h[u / 2]);
        u >>= 1;
    }
}
1
2
3
4
5
6
7
8

down 操作

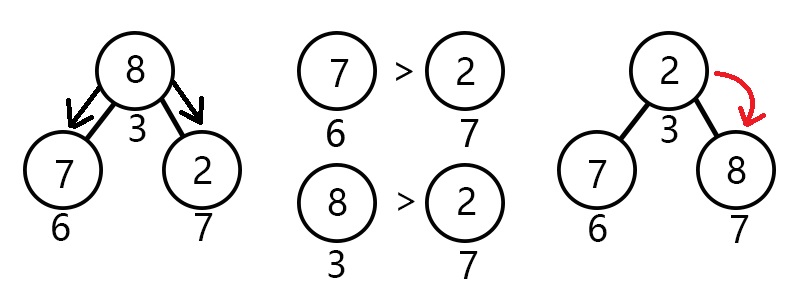
这一次 up 完毕之后呢，我们又发现了一个问题，貌似节点 3 (元素 8 )不太合适放在那，而它的子节点 7 (元素 2 )好像才应该在那个位置。此时应该让节点 3 下沉！那么问题来了：节点 3 应该往哪下沉呢？我们知道，小根堆是尽力要让小的元素在较上方的节点，而下沉与上浮一样要以交换来不断操作，所以我们应该让节点 7 与其交换。

由此我们可以得出 down 的算法了：

让当前结点的左右儿子(如果有的话)作比较，哪个比较小就和它交换，并更新询问节点的下标为被交换的儿子节点下标，否则退出。

模拟操作图示：

void down(int u)
{
    int t = u; // t 表示三个点中的最小值
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2; // 左儿子
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//右儿子
    
    if (u != t) // 如果当前的父亲不是最小的，就交换，并递归处理
    {
        swap(h[u], h[t]);
        down(t);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

其他操作

插入操作：

如何在插入的时候维护堆的性质呢？每次插入的时候我们都在最后一个位置cnt 插入，然后 up(cnt)

弹出操作：

输出栈顶元素，也就是输出最小值。输出栈顶元素，然后让最后一个元素和栈顶进行交换，然后让现在的根元素 down 就可以了。

初始化堆操作

//o(n)建堆
for (int i = n / 2; i; i --) down(i);
1
2

i 为什么从 n/2 开始 down？

首先要明确要进行 down 操作时必须满足左儿子和右儿子已经是个堆。

开始创建堆的时候，元素是随机插入的，所以不能从根节点开始 down ，而是要找到满足下面三个性质的结点：

1. 左右儿子满足堆的性质。

2. 下标最大（因为要往上遍历）

3. 不是叶结点（叶节点一定满足堆的性质）

那这个点为什么是 n/2 ？

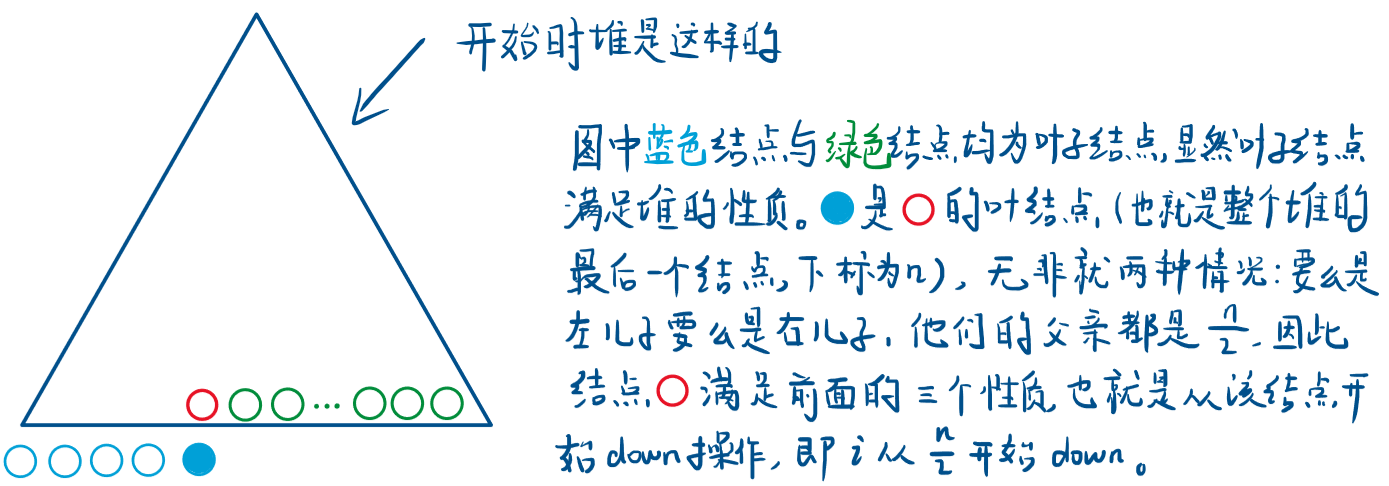
通俗的说：从 n/2 开始，还有一个角度可以理解，因为 n 是最大值，n/2 是 n 的父节点，因为 n 是最大，所以n/2 是最大的有子节点的父节点，所以从 n/2 往前遍历，就可以把整个数组遍历一遍。

Q：为什么不能从根节点开始沉啊，为什么满足三个性质才能沉呢 ？

A：因为读进来的数是随机的，你建堆的时候可能根节点小于他的左右儿子，而根的左右儿子大于他们的左右儿子，这样排出来的数组就不对了，所以只能自下而上沉。

手写堆

手写实现堆的几个操作：

1. 插入一个数
2. 求集合中的最小值
3. 删除最小值
4. 删除任意一个元素
5. 修改任意一个元素

例题：

原题链接：AcWing 838. 堆排序

堆排序补充

1. 堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序， 它的最坏、最好、平均时间复杂度均为 $O(nlogn)$， 它也是不稳定排序。

2. 堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值， 这种情况称为大顶堆，注意:没有要求结点的左孩子的值和右孩子的值的大小关系。

3. 每个结点的值都小于或等于其左右孩子结点的值， 这种情况称为小顶堆。

4. 大顶堆举例说明：

---

5. 小顶堆举例说明：

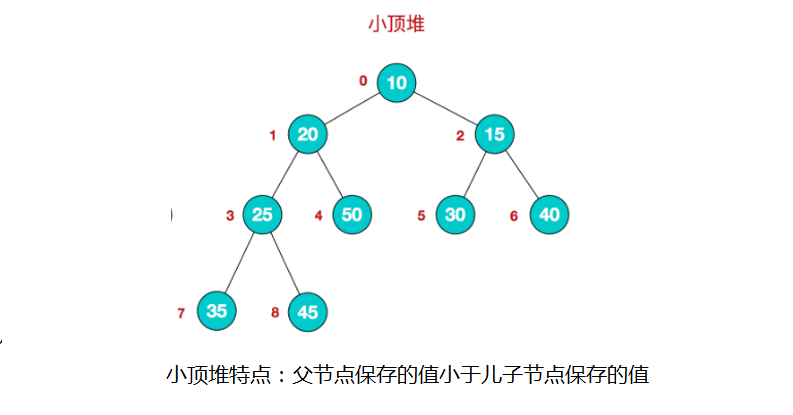
6. 一般升序采用大顶堆， 降序采用小顶堆。

基本思想：

1. 将待排序序列构造成一个大顶堆。
2. 此时，整个序列的最大值就是堆顶的根节点。
3. 将其与末尾元素进行交换， 此时末尾就为最大值。
4. 然后将剩余 n - 1 个元素重新构造成一个堆， 这样会得到 n 个元素的次小值。 如此反复执行， 便能得到一个有序序列了。
5. 可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了。

图解：

数组 {4,6,8,5,9} 要求使用堆排序法，将数组升序排序(升序采用大顶堆，降序采用小顶堆)。

6.1 构造堆

1. 将给定无序序列结构如下。

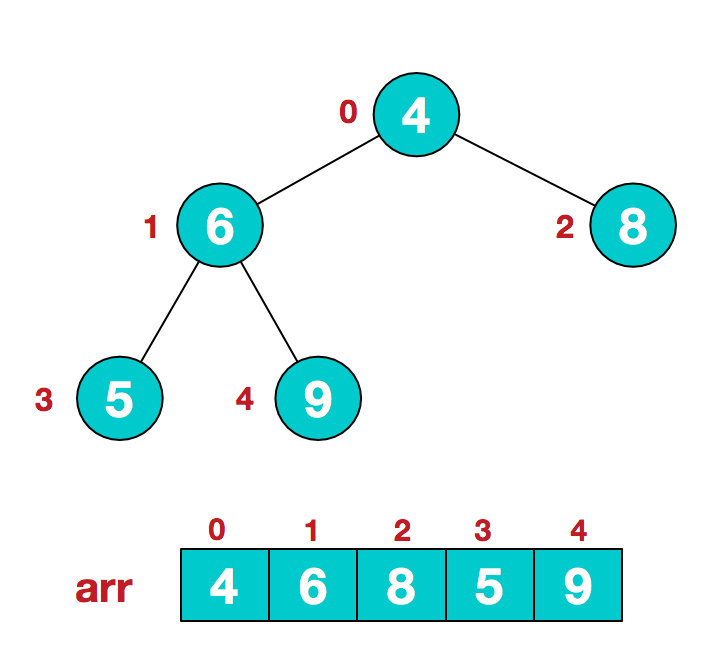
2. 从最后一个非叶子结点开始，从右至左，从下至上进行调整。
   调整规则：找到该节点和他的所有儿子。如果该节点中存的值是找到节点值中的最大值，则不进行调整。如果不是，就将该节点的值和最大值进行交换，然后递归的调整和该节点交换值得那个节点。如下图：

​ 最后一个非叶子结点开始（也就是下面的 6 结点），从左至右，从下至上进行调整。6 有两个儿子：5 和 9，这三个值中 9 最大。6 和 9 交换。

​ 因为 6 和 9 交换了，递归处理现在保存 6 的那个节点，发现它没有儿子，停止递归。

​ 找到第二个非叶节点 4 ，由于[4, 9, 8]中 9 元素最大，4 和 9 交换。

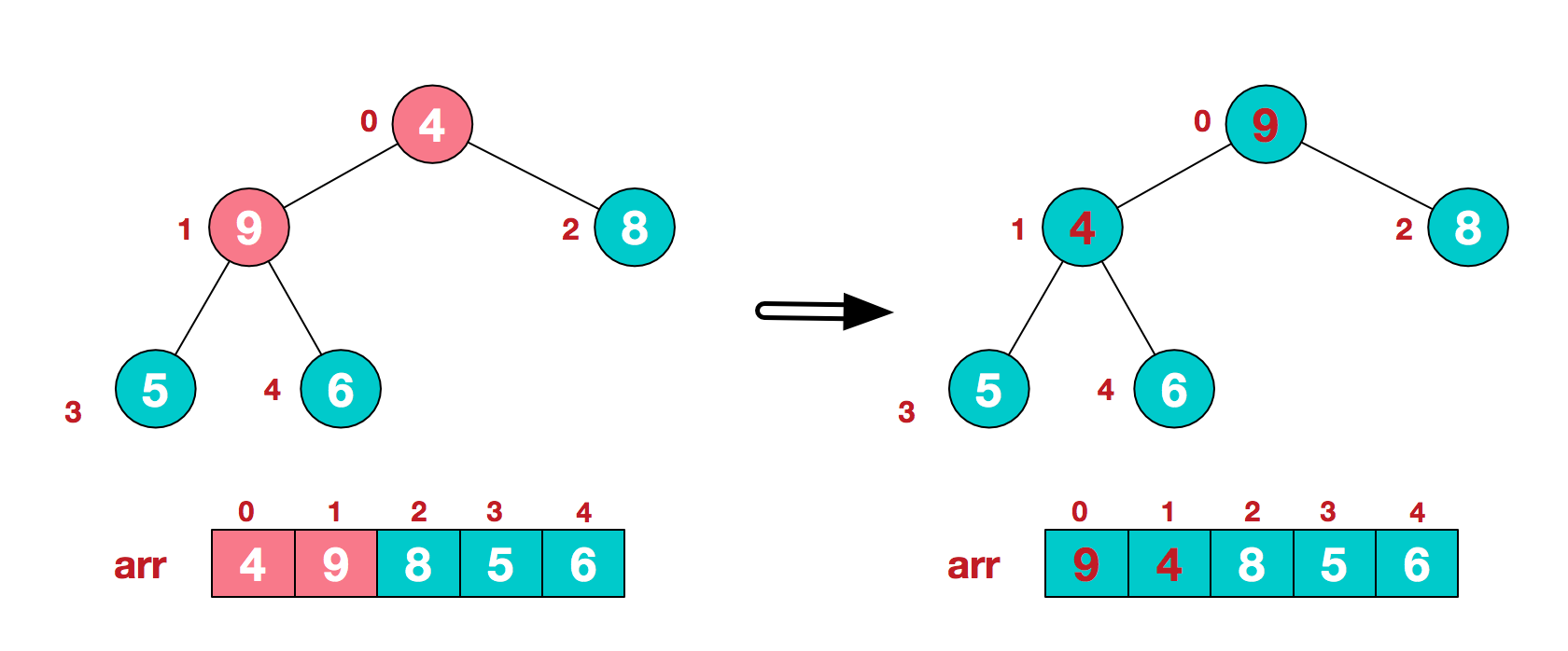
​ 因为 4 和 9 交换了，递归处理现在保存 4 的那个节点: 找到它的两个儿子：5, 6, 其中 6 最大，交换 4 和 6。

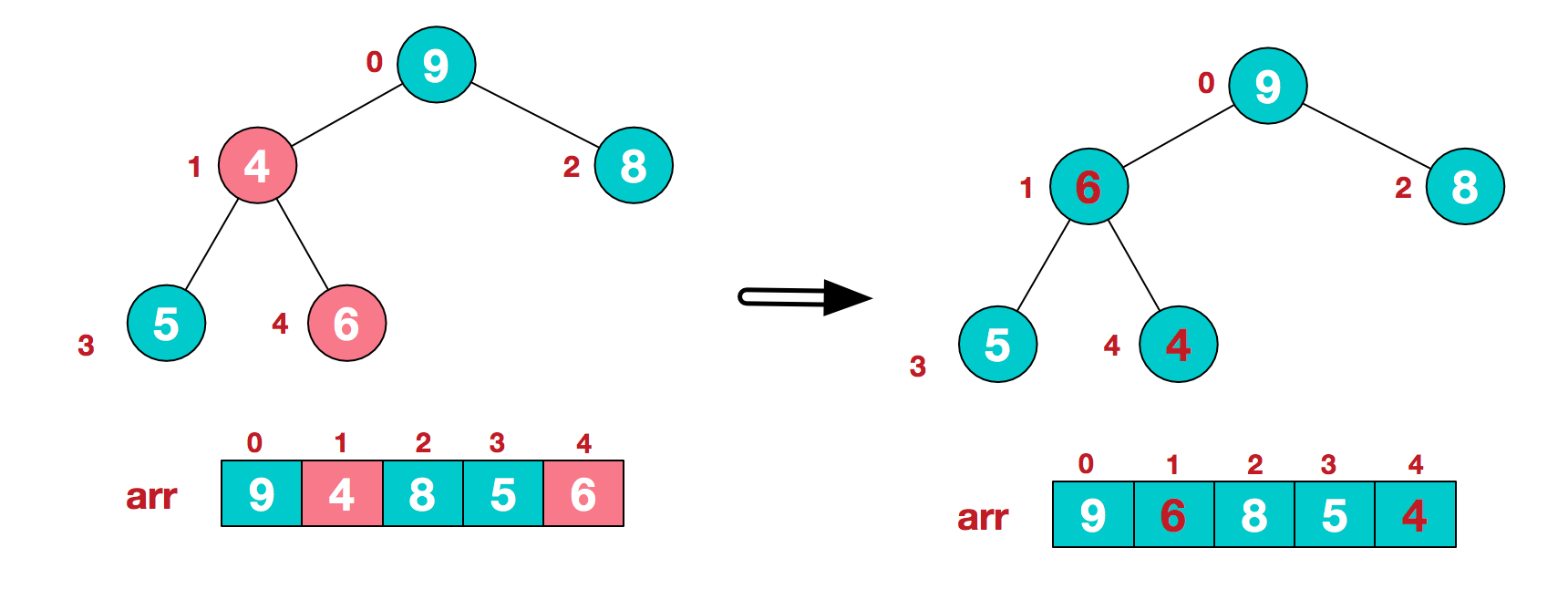
​ 然后继续递归处理，发现现在保存 4 的节点没有儿子，停止。

​ 此时，我们就将一个无序序列构造成了一个大顶堆。

6.2 排序

将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。如下图：

• 将堆顶元素 9 和末尾元素 4 进行交换。

  

• 重新调整结构（规则如上），使其继续满足堆定义

  

• 再将堆顶元素 8 与末尾元素 5 进行交换，得到第二大元素 8。

  

• 后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序。

  

6.3 总结：

1. 将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆。

2. 将堆顶元素与末尾元素交换，将最大元素”沉”到数组末端。

3. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

6.4 完整代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], cnt; //cnt 表示heap中有多少元素。下标从 1 开始

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;

    for (int i = n / 2; i; i -- ) down(i);

    while (m -- )
    {
        printf("%d ", h[1]);
        h[1] = h[cnt -- ];
        down(1);
    }

    puts("");

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

参考资料：

基本数据结构――堆的基本概念及其操作

堆排序 分析i = n/2 开始初始化

AcWing 838. 堆排序

本文供自己复习数据结构所用