成人生命周期中的脑白质微结构：使用高级扩散模型和脑龄预测的纵向和横断面的混合研究_jhu 白质图谱

人类大脑白质的宏观和微观结构在整个发育和衰老过程中都经历了实质性的变化。当前的研究者对这些描述整个生命周期的人脑的空间和时间特征的大部分了解来自磁共振成像(MRI)，包括扩散磁共振成像(dMRI)，它能够以前所未有的灵敏度和细节对脑白质进行可视化和量化。然而，以前绝大部分研究依赖于横断面设计、有限的年龄范围和基于常规单壳（即单b值）磁共振成像的扩散张量成像(DTI)。

在本项研究中包括了702个多壳dMRI数据集的横断面和纵向(平均间隔15.2个月)混合研究，结合互补的dMRI模型研究了18-94岁(57.12%的女性)健康人的白质微观结构的年龄轨迹。

结果表明，传统DTI指标(各向异性分数[FA]、平均扩散系数[MD]、轴向扩散系数[AD]、径向扩散系数[RD])的年龄斜率与以前的研究基本一致，最高性能的高级dMRI模型显示出与传统DTI相当的年龄预测精度。线性混合效应模型和Wilk’s定理分析表明，RSI模型的‘FA fine’度量和NODDI模型的‘方向分散度’(OD)度量对年龄的敏感性最高。本文结果表明，高级扩散模型(DKI、NODDI、RSI、SMT-mc、WMTI)提供了与年龄相关的脑白质微结构变化的灵敏测量，它们补充和扩展了常规DTI提供的白质微观信息。本文发表于NEUROIMAGE杂志。

引言

人脑白质的结构在一生中都在经历不断的重塑。白质宏观和微观结构的年龄相关轨迹通常反映了儿童、青春期和成年早期各向异性的增加和扩散率的减少，以及随后的各向异性减少和扩散率的增加。由于该领域主要由横断面研究占据主导地位，从设计上缺乏关于个体轨迹的信息。因此，虽然过去十年的部分纵向研究显示，在发育和衰老过程中，白质也发生了相应的变化。但目前在广泛的年龄范围内评估个体变化差异的研究并不多见。

研究者们通常使用传统扩散张量成像(DTI)来研究白质特性，该类研究基于包括：各向异性分数(FA)、平均扩散率(MD)、轴向扩散率(AD)和径向扩散率(RD)在内的DTI指标对年龄的高度敏感。然而，传统DTI指标存在很多局限性，比如它们无法捕捉受限的非高斯扩散，并且缺乏对不同扩散组织的特异性。这些局限性促使了更高级的扩散磁共振(dMRI)模型的不断发展。这些模型包括扩散峰度成像(DKI)，它是为了在扩散信号中添加受限扩散或非高斯性而开发的；神经突起方向离散度与密度成像(NODDI)，它模拟了三种类型的微结构环境：细胞内、细胞外和负责脑脊液(CSF)所占空间的各向同性水质子区域；白质束完整性(WMTI)，它从轴突内和轴突外环境中获得微结构特征；限制波谱成像(RSI)，它应用线性混合模型来解析长度尺度的波谱，同时获取几何信息；多组分球平均技术(SMT-mc)，这是一种不受纤维交叉和方向分散度影响的微观扩散各向异性成像方法。

这些模型通常基于具有多个扩散权重的多壳采集，它们大致可以分为“信号”表示方法和“组织”模型。包括DTI和DKI在内的信号表示方法描述了体素中的扩散信号行为，没有关于潜在组织的假设。但由于估计参数缺乏特异性，它们对组织微结构的表征仍然是间接的。组织模型(包括NODDI、RSI、SMT-mc和WMTI)涉及对底层组织几何形状的估计，这可能提供了更高的生物学特异性和更精确的白质微结构和结构测量。然而，尽管组织模型的设计提高了特异性，但它们要求对潜在微结构的假设是准确的。

在神经成像大数据带来的机会的基础上，最近许多研究者利用机器学习技术研究了与年龄相关的大脑变化，例如脑龄预测；根据神经成像数据估计大脑的“生物”年龄。预测大脑的年龄，然后观察预测的年龄和实际年龄之间的差异，可以生成一个用来表示大脑完整性的重要个性化标记，这些标记可能能够揭示神经和神经精神障碍的风险。虽然脑龄预测在最近几年变得更加流行，但大多数研究都使用了灰质特征来预测脑年龄，只有少数研究专门使用或部分使用了dMRI。并且，RSI和NODDI等高级扩散模型的脑龄预测精度尚不清楚。

本研究包括从573名18-94岁的健康人(拥有702个多壳dMRI数据集)获得的横断面和纵向数据，主要目的是通过比较不同dMRI指标的相关曲线参数(如关键偏转点和变化率以及年龄预测精度)来全面描述成年后与年龄相关的标准白质轨迹，特别关注基于高级(DKI、NODDI、RSI、SMT-mc和WMTI)扩散模型计算出的相对新的参数，并比较其和传统(DTI)扩散模型的白质微观结构的一致性。

本文首先估计了每个扩散指标在年龄范围内的轨迹。其次，使用三种不同的方法来比较扩散模型的年龄敏感性：

1.使用包括年龄、性别、时间点在内的线性混合效应模型(lme)；

2.对于每个模型，进行了有年龄项和无年龄项的拟合，并使用Wilk’s定理比较了拟合似然度；

3.基于扩散度量使用机器学习来预测年龄，并比较了这些模型的预测精度。之后，研究了lme模型的每个年龄曲线函数的导数，以确定每个扩散指标的轨迹变化点。基于先前用一系列扩散MRI指标表征年龄差异和纵向变化的工作，本文预计纳入的指标将显示出与年龄的曲线-线性关系，不同的轨迹和偏转点可能反映了脑老化不同阶段的假定的生物基础在生命周期中的不同参与度和变化速度。

方法和材料

样本描述

最初的样本包括来自两项综合研究的754个健康受试者的多壳dMRI数据集。在质量检测(QC)后删除52个数据集之后，最终样本包括来自573个个体的702个数据集，包括129名参与者的纵向数据(两个时间点，平均间隔=15.2个月)。人口统计信息汇总在表1和图1中。排除标准包括神经和精神障碍，以及既往头部创伤。此研究已得到地区伦理委员会的批准，所有参与者都提供了书面知情同意。

表1：与研究样本有关的人口统计学信息

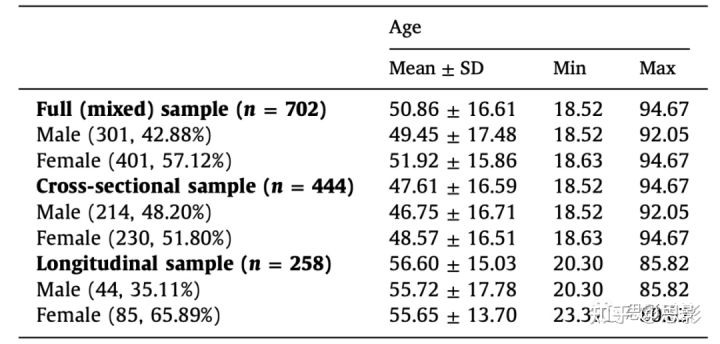
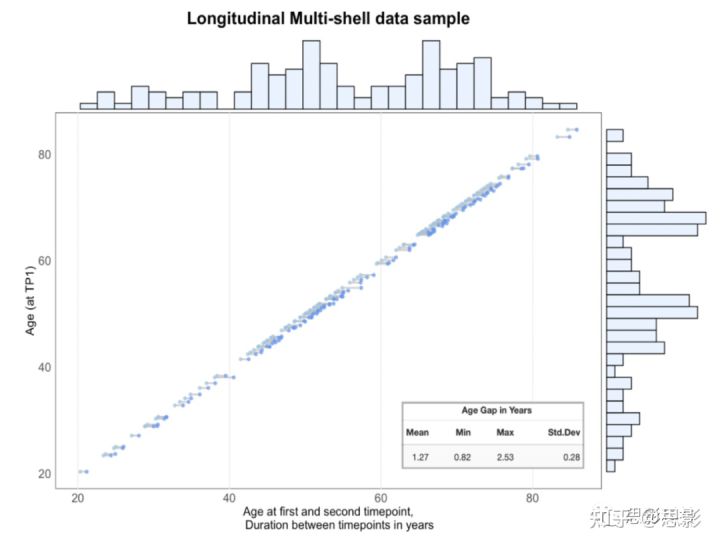
图1：完整纵向样本的时间点1和时间点2之间的间隔，n=258(129名受试者)。直方图表示数据点密度。

MRI采集

图像采集使用32通道头线圈的GE MR750 3T扫描仪。dMRI采用自旋回波平面成像(EPI)序列，参数为：TR=8150ms；TE=83.1ms；翻转角=90°；FOV：256×256 mm；层厚=2 mm，平面内分辨率=2 mm。我们得到了b=0、沿60个方向的b=1000s/mm2和 沿30个方向的b=2000 s/mm2的10次扩散加权数据的采集。此外，还获得了7次b=0的反转相位编码方向的数据，用于校正磁化率失真。

dMRI处理

处理步骤包括噪声校正、gibbs校正（一种新的噪声校正方法，可以使用dipy或者mrtrix3实现）、使用FSL中的topup和eddy做头动校正和涡流校正。各向同性平滑是用fslmaths函数实现的，高斯核为1mm。使用FSL中的dtifit工具估计DTI，并从中排除b=2000壳。利用多壳数据，使用MatLab代码(https://github.com/NYU-DiffusionMRI/DESIGNER)估计DKI和WMTI指标。NODDI度量是使用MatLab(https://github.com/daducci/AMICO)中的AMICO导出的。SMT-mc指标与原始代码(https://github.com/ekaden/smt)相匹配。RSI指标使用内部的MatLab工具进行评估。

基于最近的研究，本文从六个模型(DTI、DKI、NODDI、RSI、SMT mc、WMTI)中选择了20个标量指标。我们还根据与我们的采集协议相关的可行性和开源脚本的可用性来选择模型。出于说明性目的，图2显示了一个参与者的所有用到的指标。使用从一系列感兴趣区域提取的所有可用指标进行脑龄预测。

图2：来自一个参与者的扩散指标。

DTI：FA(各向异性分数)、MD(平均扩散系数)、AD(轴向扩散系数)、RD(径向扩散系数)。

DKI：AK(轴向峰度)、MK(平均峰度)、RK(径向峰度)。

NODDI：ICVF(细胞内体积分数)、ISOVF(各向同性体积分数)、OD(方向分散度)。

RSI：CI(细胞指数)、Fine(FA fine scale/slow compartment)、rD(限制扩散系数)。

SMT mc：exMD(细胞外间隙)、exTr(横向细胞外间隙)、Intra(轴突内扩散率)。

WMTI：Awf(轴突含水率)、aEAD、aIAD(轴向内外弥散系数)、rEAD(轴向轴突外弥散系数)。

质量检测步骤

本文实施了严格的质量控制程序，以确保数据质量不受运动、噪声或伪影的影响。本文得出了各种质量评估(QA)指标，包括时间信噪比(TSNR)。如果认为数据质量不满意，则手动检查并重新移除离群值。总共删除了52个数据，删减后的数据集包括n=702次扫描。之后对这一数据集进行相同的目测检查。作为额外的步骤，人工检查图像时间信噪比的Z分数是否偏离平均值±2.5倍的标准差。在这一步骤之后，最终数据集保持在来自573个人的702次扫描。

基于白质骨架的弥散统计分析(TBSS)

使用FSL软件，通过基于白质骨架的弥散统计分析(TBSS)对FA数据进行体素级的统计分析。首先，使用BET对FA图像进行脑提取，并使用非线性配准工具FNIRT将FA图像配准对到FMRI58_FA模板空间，FNIRT使用b-Spline表示配准的空间扭曲场。接下来，创建并细化所有受试者的平均FA图像，以创建平均FA骨架，该骨架表示组中所有共同的纤维束的平均。然后，将每个受试者对齐的FA数据投射到这个骨架上。平均FA骨架的阈值设为FA>0.2。对所有指标重复此过程。使用概率白质图谱(JHU)，以fslmeants函数来提取平均骨架和20个感兴趣区域(ROI)的各个指标的值。包括平均骨架值在内，每个人获得了420个特征(20*21)(20个指标，20+1个ROI，加的那个“1”就是平均骨架)。将20个指标分别用于年龄曲线轨迹的拟合、lme分析和Wilk’s定理分析。将所有420个MRI特征用于年龄预测。对573名参与者(不包括纵向测量)进行了额外的体素分析，使用FSL工具的随机化置换检验和无阈值集群增强方法(TFCE)，运行了5000次置换检验，以测试每个扩散指标与年龄的关联。

扩散度量的重复性

不同扩散模型的有效性和敏感性主要取决于用于模型拟合的数据的丰富性、质量和特性。为了评估研究中使用的高级指标的重复性，使用从不同采集方案中获得的数据来估计dMRI模型，这些数据来自23个平均年龄为35.77岁的健康受试者。这代表了整个样本的一个子样本。比较了以下三种采集方案：1)b=[1000,2000]与[60，30]个方向，与主要分析中使用的采集方案相同；2)b=[1000,2000]与[60，60]个方向；3) b=[1000,2000,3000]与[60，60，60]个方向。对于每个方案，使用与前文叙述的方法的相同的处理数据方式，并提取每个指标的平均骨架值。采集方案之间的比较是使用三种采集协议获得的每种指标平均骨架值的箱式图(SI图4)、年龄作为平均骨架值函数的自变量的散点图(SI图5)以及皮尔逊相关系数图(SI图6)进行的，其中方案1由方案3分解得出。(仅展示SI图4供读者理解)。

图S4:利用子样本得到的三种采集协议获得的每种指标平均骨架值的箱式图

统计分析

所有的统计分析都使用3.6.0版本的统计环境R和Python3.7.0进行。

线性混合效应模型(lme)

为了研究年龄与每个扩散指标的全脑平均骨架值之间的关系，使用R中的lme函数进行了lme（线性混合效应模型）分析。在拟合模型时，对每个变量进行了z标准化，并将年龄、正交化的年龄2、性别和时间点(TP)作为固定效应。被试的ID是作为随机效应输入的。对于每个扩散度量M，采用以下函数：

M = A + B×Age + C×Age2+ Sex + TP

其中A是截距，B是年龄系数，C是正交化的年龄二次项的系数。使用R中的预测函数从拟合的模型中预测得到年龄曲线，并用于年龄曲线轨迹图。对残差进行检测后发现结果符合方差齐性和正态分布。显著性阈值设置为p<0.05，并使用FDR对结果进行多重比较校正。

为了研究每条年龄曲线在任意点的变化率，我们使用有限差分数值微分法计算了它们的导数。为了比较模型的年龄敏感性，我们分别用年龄项和不用年龄项运行了lme的fits函数(拟合)，并计算了似然比的差异。年龄依赖性的显著性是使用Wilk’s定理计算的，公式是

其中，L2是从带有年龄项的模型中获得的似然比，L1是从没有年龄项的模型中获得的似然比。

脑龄预测

使用XGBoost回归模型进行脑龄预测，该模型包括一种基于决策树的集成算法，该算法已被用于最近的大规模脑龄研究。参数设置为最大深度=3，estimators参数=100，学习率=0.1(默认)。对于每个扩散模型(DTI、DKI、NODDI、RSI、SMT -mc、WMTI)，通过10折交叉验证估计预测年龄，为每个个体进行特定于模型的脑龄估计，以及基于所有扩散特征的多模态脑龄估计。为了考察每个模型的预测精度，对预测年龄与实际年龄进行了相关分析，并计算了特定模型的R2、均方根误差(RMSE)和平均绝对误差(MAE)。为了在统计学上比较模型的预测精度，对相关样本进行Z检验，以成对的方式对预测年龄和实际年龄之间的特定模型相关性进行检验，Z检验公式如下：

m1和m2代表模型1和模型2，β代表回归拟合的β值(也就是估计的回归系数)，σ代表误差，ρ表示两组间的相关性。为了评估不同模型的互补的价值，我们计算了脑龄预测之间的相关性(图6)。使用线性模型对这些预测的年龄偏差进行了修正，并将残差用于相关性分析。

为了评估每个扩散模型在多模态模型中的重要性，我们使用了一个额外的预测模型，该模型只包括平均骨架值以减少回归的输入中高度相关的特征的数量，而后计算了每个模态贡献的总权重的比例，其中，总权重表示一个特征在所有(决策)树上都被用于分割数据的次数。又计算了增益值，它表示将一个特征添加到它所在的分支上之后，精度提高的程度。为了评估总体模型性能的显著性，使用重复10次的分成10份的交叉验证计算了多模态模型的平均均方根误差，并与随机1000次的置换检验的零分布进行了比较。

图6：不同模型预测脑龄之间的相关性

结果

扩散度量的重复性

根据不同采集计划(方法部分的“扩散度量的重复性”章节已详细介绍)获得的数据估算的扩散指标的重复性表明，所有模型指标的平均骨架值之间总体上具有很高的相关性。NODDI的OD指标和RSI的rD指标的总体重复性最高。重复性最差的是WMTI的radEAD指标。SI图四已展示部分代表性结果，其他结果可详见原文补充材料SI5-SI7。

年龄轨迹

图3显示了线性混合效应模型得出的每个扩散指标的年龄曲线，将该曲线作为年龄的函数，其中，年龄曲线与lme模型的预测值进行了拟合。图4在一个曲线图中以标准化形式显示了图3中所有lme模型得出的年龄曲线。图5展示了lme拟合的导数，提供了每个点（年龄）的估计变化率，包括每个模型曲线的轨迹变化点和转折点的陡峭程度。

图3：年龄曲线，其中每个扩散度量的标准化(z分数)平均骨架值(y轴)被绘制为年龄(x轴)的函数。

用lme得出预测值拟合线。阴影区域代表95%的可信区间。由直线连接的点表示纵向数据，其中圆形是第一个时间点，三角形是第二个时间点。男性受试者用粉色表示，女性受试者用绿色表示。

图4：以标准化形式显示图3中所有lme模型得出的年龄曲线

图5：每个扩散模型的导数，提供每个点的估计变化率。

X轴上拟合线在y轴上与0相交的点表示每个指标的年龄轨迹的转折点。

比较年龄曲线

图3显示了所有指标的估计年龄曲线。简而言之，FA在30岁后稳步下降，50岁后下降幅度更大。MD、AD和RD遵循相反的变化规律，在40岁左右前减小，此后轨迹增加。DKI的指标都显示出曲线形轨迹，NODDI的ICVF指标、RSI的CI指标、SMT mc 的intra指标和WMTI的awf指标也都遵循类似的轨迹。RSI的rD指标、RSI的FA fine指标和WMTI的 axIAD指标遵循从始至终的递减轨迹。SMT mc的 exMD和exTr指标，以及WMTI的radEAD指标遵循与MD和RD相似的轨迹。NODDI的OD指标和ISOFV指标显示出随着年龄的增长，其中OD指标的斜率降低成相对稳定的变化。最后，WMTI的 axEAD指标显示出U形轨迹。

使用lme模型估计年龄敏感性

lme模型的结果显示，年龄对所有扩散指标的全脑平均骨架值有显著的主效应。对年龄项的固定效应估计(β)的检验和t检验可以解释与年龄的线性相关的程度和方向。总体而言，RSI的FA fine指标对年龄最为敏感。NODDI的OD指标对年龄的敏感性次之。对年龄最不敏感的模型为DTI的AD指标。在常规DTI指标中，FA对年龄最为敏感。没有时间点的主效应通过多重比较校正。

用Wilk’s定理估计年龄敏感性

表3显示了通过似然值差异估计每个指标的整体年龄依赖性。所有指标均表现出显著的年龄依赖性，其中RSI的FA fine是最敏感的年龄指标，其次是NODDI 的OD指标和基于DTI的FA指标。WMTI的axEAD是年龄依赖性最小的指标。

表3：没有年龄项(L1)和有年龄项(L2)的LME模型的似然值。使用Wilk’s定理通过似然值的差异来估计年龄依赖性的显著性

用脑龄估计年龄敏感度

多模态和特定于模型的脑龄预测的模型性能如表3所示。SI图8和9显示了每个模型的预测年龄和实际年龄之间的关联。图6显示了每个模型的预测年龄之间的成对的相关性。图7和图8显示了模型的年龄预测精度的成对差异。从表3可以看出，多模态模型对年龄的预测最准确，而DKI模型表现最差。如图7和图8所示，多模态模型的预测精度显著高于其他各模型的精度，其中多模态模型与DKI之间的差异最大。DTI、RSI、WMTI和NODDI之间的预测精度差异在多重比较校正后没有显著性。图6显示了DTI、RSI、NODDI、SMT和WMTI预测之间的平均相关系数r=0.59，而DKI与其他模型的相关性较低(平均r=0.29)。

表4：每个模型的MRI变量数(对应于度量特征的总和)、均方根误差(RMSE)、平均绝对误差(MAE)、预测年龄与实际年龄之间的相关性以及R2。

SI图8：每一种特定模态的预测年龄和实际年龄之间的关联

SI图9：多模态模型的预测年龄和实际年龄之间的关联

图6：每个模态和多模态模型的脑龄预测的相关矩阵

图7：基于相关样本的z检验，显示模型预测精度

讨论

衰老会导致一系列大脑结构的改变，对支撑认知和其他复杂大脑功能的神经回路的微观和宏观结构特性产生影响。在目前的横断面和纵向混合研究中，本文基于先进的和传统的dMRI模型，比较了成人生命周期中的年龄敏感性和脑白质年龄轨迹。本文的综合分析方法的结果包括年龄曲线轨迹、线性混合效应模型、Wilk’s定理分析和脑龄预测。结果发现，所有扩散指标的年龄敏感性都很高，性能最高的高级dMRI模型和常规DTI模型之间具有相当的灵敏度。并且，将所有指标包含在同一模型中具有一定的好处。混合效应分析和相应的导数揭示了不同模型之间年龄轨迹的差异，表明它们可能对白质老化的不同潜在方面敏感性高。

本文的结果表明，FA在30岁阶段处于平稳期，在40岁阶段斜率逐渐下降，在衰老期下降加速(图3)。MD、AD和RD等其他DTI指标显示，在40-50岁年龄段之前，扩散率下降，随后其轨迹在一段时间内保持稳定，而后上升。虽然这些结果在很大程度上与之前的研究中观察到的轨迹一致，但本文的研究结果中的倒U形不那么突出，可能是因为缺乏20岁以下的年轻参与者。有趣的是，基于相对简单的DTI模型的FA仅利用单壳数据，却取得了年龄敏感性最高的结果之一，这个结果支持了DTI提供了白质解剖和神经病理变化的敏感指标这一结论。此前，传统DTI指标中生命周期差异的特征曲线轨迹被认为反映了儿童期、青少年期和成年早期与髓鞘相关的成熟，以及随后在成年后期和衰老期间脱髓鞘之间的联系。然而，DTI指标不能区分轴突内和轴突外的间隔，而且它们还可能受到个体差异和交叉纤维以及轴突堆积和密度变化的影响。DTI指标的具体生物学解释基本上取决于局部纤维结构，DTI信号的变化需要仔细的解释，因为它不能直接推断出确切的神经生物学基础。除了常规的DTI外，使用先进的dMRI模型可能会在解释结果时提供更多的特异性，并通过分离同时发生的各种生物源来提高组织病理学的描述精度。

虽然几个先进的dMRI模型在年龄敏感性方面显示出与DTI类似的结果，但它们也显示了明显不同的年龄轨迹(图3)，包括转折点的变化(图4)，表明了各向异性和扩散率指标在什么年龄时方向发生变化，以及变化的梯度(图5)，表明了指标下降/升高的速度。使用每个模型的导数计算的转折点和变化梯度的变异性，除了提供了在不同生命阶段不同指标之间的差异敏感性外，还向我们提供了特定年龄段的估计变化速度。虽然扩散成像不能在细胞水平上直接了解神经元的过程，但高级dMRI模型中不同的估计轨迹可能反映了脑老化不同阶段假定的生物学基础的不同的参与程度。因此，指标的特异性差异可能反映每个dMRI模型背后与年龄相关的病理变化，这能够帮助我们更好地定位白质微结构开始下降的年龄，这对旨在促进健康老化的干预策略具有重要意义。

尽管最近的研究已经证实DTI的FA和RD指标是髓鞘的敏感标记物，但在仅以DTI为基础解释特定的潜在生物学基础时必须谨慎。考虑到这一点，将NODDI、WMTI、RSI和SMT mc等组织模型相结合可能在联合反映与大脑老化相关的神经生物学基础方面更具有希望。例如，WMTI指标已被验证能够反映轴突内和轴突外的潜在生物学差异。WMTI的awf指标被发现与轴突密度有关，而WMTI的radEAD指标在一定程度上描述了髓鞘化的程度，并与充满组织间液和大分子的细胞外环境以及血管和血管周围间隙有关。NODDI模型的参数图显示了与已知的脑解剖学一致的组织分布的空间模式。作为先进扩散模型为研究提供可行性的一个例子，NODDI模型可以分离影响FA的两个主要因素——轴突密度和方向分散度。RSI模型直径的计算已被证明与大鼠脑内无髓轴突和有髓轴突的直径相一致，这表明了直接的生物学解释。同样，组织学分析表明，SMT mc微观扩散系数对病理组织改变具有直接敏感性。虽然DKI不是组织模型，但它提供了细胞间隔和细胞膜的特定测量，并且相对不受大分子浓度的影响，潜在地提供了比传统DTI更具体的组织特性指标。

从理论上讲，不同扩散磁共振模型的部分不重叠的假设和生物物理性质提供了一个更全面和完整的观点，当将多种模型联合考虑时，可以更全面地了解大脑发育、衰老和疾病的多样化的生物学过程。总体而言，本文在结合不同模型时的年龄预测准确率更高的这一发现支持了这种观点。然而，几个不同指标的相对较高的相关性和相似的年龄相关轨迹也表明了一定程度的冗余。还需要进一步的研究来检验这种假设，即结合大脑宏观和微观的各种扩散磁共振模型的多模态数据驱动的大脑表型方法(例如“指纹”)有助于提高在更具体的临床应用中和预测中的可行性和精度。我们还需要考虑到，与传统的DTI相比，高级模型不仅可以提高特异性，而且可能提供与髓鞘和轴突重组相关的额外信息，同时，高级模型特定地模拟了DTI通常合并的微结构特征，如轴突密度、轴突直径和轴突方向分散度。还需要进行进一步的研究来验证和开发dMRI模型，以更好地反映白质的不同生物学和几何特性。如果对潜在微结构的假设是有效的，这些先进的模型将为研究脑发育和老化以及在各种临床条件下的异常脑生物学做出更大的贡献。

在考虑一系列扩散模型时，重要的是要注意每种模型的局限性。近年来，NODDI受到了很大的批评，有研究表明NODDI的模型假设是无效的。NODDI仅提供几何参数的估计，没有任何直接的扩散系数估计。与DTI一样，DKI的特异性有限，因为它会受到不同组织微结构特征的影响。因此，研究提出了DKI参数与白质微结构直接相关的生物物理模型，也就是WMTI。然而，WMTI中的假设可能过于简单化，这可能会导致估计参数的偏差，从而减少关于显微组织的信息。据说，WMTI参数估计的精度也会随着方向分散度(OD)的增加而逐渐降低。

SMT mc模型克服了WMTI和NODDI的局限性，因为它没有对轴突的取向分布做出假设。然而，该模型基于神经突内的有效横向扩散率为零的假设，这也是该模型的限制，这一近似假设可能不适用于无髓鞘轴突和树突，因为无髓鞘轴突和树突可能在微观尺度上发生轴突波动。与大多数基于扩散的技术一样，RSI也存在分辨率低的问题，作为多模态成像协议的一部分，RSI可能最好在补充高空间分辨率序列后使用。尽管每个模型都有局限性，而且它们之间可能存在冗余，但使用扩散模型的组合来评估与年龄相关的白质微结构变化可能是有利的，这样便于将重点放在特殊的神经解剖学和微结构模式上。例如，WMTI和SMT mc的生物物理模型增加了评估轴突内和轴突外空间扩散产生的影响。

还必须解决一些方法上的限制。一个需要注意的问题是对感兴趣区域和整个白质骨架进行平均，这一问题因不同区域与年龄相关的方向和大小的不同而变得复杂。最近的研究发现，全脑平均骨架模型的表现优于基于感兴趣区的单一度量模型，为在全脑水平上捕获脑龄预测所需的相关信息提供了证据。事实上，之前的研究表明，基于区域DTI的局部脑老化指数与全脑的进程相关，这也得到了遗传信息方法的支持，该方法表明，很大比例的区域遗传力是由整体遗传因素解释的。其次，我们使用FA生成白质骨架。未来的研究应该考虑基于先进的扩散图生成白质骨架，这种扩散图更能抵抗交叉纤维。

这项研究的其他优点也必须得到说明。TBSS提供个体FA图的鲁棒的非线性配准和骨架，这能够支持后续的体素分析和使用一系列白质图谱提取基于ROI的统计信息。这种方法是高度标准化的，这促进了重复性分析和未来的荟萃分析。可以通过使用临床上可行的采集协议获得的数据并使用先进的计算dMRI模型来对研究所包含的dMRI指标进行重测。基于多壳数据的高级dMRI模型的组合是一个关键优势，它可能根据不同b值引起的不同组织反应提供细胞环境的更详细特征。

这项研究还包括了一个相对较大的样本，并受益于所有参与者都接受了相同核磁共振扫描仪的扫描。此外，由于横断面研究受到受试者之间的差异和可能存在的队列效应的限制，目前的研究是横断面和纵向混合设计，其中参试者可以作为他们自己的基线。然而，我们的研究在纵向方面有一些局限性，包括间隔时间较短，以及与横断面样本相比样本量较小。因此，主要结果主要是由横断面数据驱动的。未来的研究应该着眼于在几个时间点上采用完全纵向设计，以便评估个体随时间变化的差异，最好是在较大的年龄范围内。

总结：

总而言之，表征白质微结构在人类生命周期中的变化对于建立正常神经发育和衰老的可靠模型至关重要，这可以帮助我们更好地理解偏离健康年龄轨迹的情况。目前的研究表明，虽然先进的和传统的dMRI模型显示出类似的年龄敏感性，但多壳扩散成像和先进的dMRI模型有助于在多个、互补的方面测量白质特征。在生物组织特异性方面对dMRI模型进行进一步的发展仍然是理解人类一生中脑白质发育的一个具有挑战性但很重要的目标。

但要注意的是，虽然先进的dMRI模型为年龄敏感性和年龄轨迹的差异提供了新的见解，但这些指标的生物学解释需要进一步验证。需要继续开发和验证更优化的扩散模型，以更好地反映大脑的生物学特性，未来的研究应考虑可能参与调节大脑和认知发育以及衰老的一系列潜在因素的影响，例如产前和围产期的情况、社会人口因素、教育、生活方式、心脏代谢风险因素和遗传学。