基于遗传模拟退火的聚类算法(matlab实现)_退火聚类

微♥关注“电击小子程高兴的MATLAB小屋”获取专属优惠

1 理论基础

1.1 模糊聚类分析

    模糊聚类是目前知识发现以及模式识别等诸多领域中的重要研究分支之一。随着研究范围的拓展，不管是科学研究还是实际应用，都对聚类的结果从多方面提出了更高的要求。模糊C-均值聚类(FCM)是目前比较流行的一种聚类方法。该方法使用了在欧几里得空间确定数据点的几何贴近度的概念，它将这些数据分配到不同的聚类，然后确定这些聚类之间的距离。模糊C-均值聚类算法在理论和应用上都为其他的模糊聚类分析方法奠定了基础，应用也最广泛。但是，从本质上FCM算法是一种局部搜索优化算法，如果初始值选择不当，它就会收敛到局部极小点上。因此，FCM算法的这一缺点限制了人们对它的使用。

1.2 模拟退火算法

    Metropolis等人于1953年提出了模拟退火算法(SA),其基本思想是把某类优化问题的求解过程与统计热力学中的热平衡问题进行对比，固体退火过程的物理图像和统计性质是模拟退火算法的物理背景，Metropolis接受准则使算法跳离局部最优的“陷阱”,而冷却进度表的合理选择是算法应用的前提。固体退火是先将固体加热至熔化，然后徐徐冷却使之凝固成规整晶体的热力学过程。从统计物理学的观点看，随着温度的降低，物质的能量将逐渐趋近于一个较低的状态，并最终达到某种平衡。

1.3 遗传算法

    遗传算法(GA)的主要思想是基于达尔文的生物进化论和孟德尔的遗传学。遗传算法结合了达尔文的适者生存和随机交换理论，是一种自然进化系统的计算模型，也是一种通用的求解优化问题的适应性搜索方法。遗传算法在运行早期个体差异较大，当采用经典的轮盘赌方式选择时，后代产生的个数与父个体适应度大小成正比，因此在早期容易使个别好的个体的后代充斥整个种群，造成早熟。在遗传算法后期，适应度趋向一致，优秀的个体在产生后代时，优势不明显，从而使整个种群进化停滞不前。因此对适应度适当地进行拉伸是必要的，这样在温度高时(遗传算法的前期),适应度相近的个体产生后代的概率相近；而当温度不断下降后，拉伸作用加强，使适应度相近的个体适应度差异放大，从而使得优秀个体的优势更明显。

    本文将模拟退火算法与遗传算法相结合(SAGA)用于聚类分析，由于模拟退火算法和遗传算法可以互相取长补短，因此有效地克服了传统遗传算法的早熟现象，同时根据聚类问题的具体情况设计遗传编码方式及适应度函数，使该算法更有效、更快速地收敛到全局最优解。

2 案例背景

2.1 问题描述

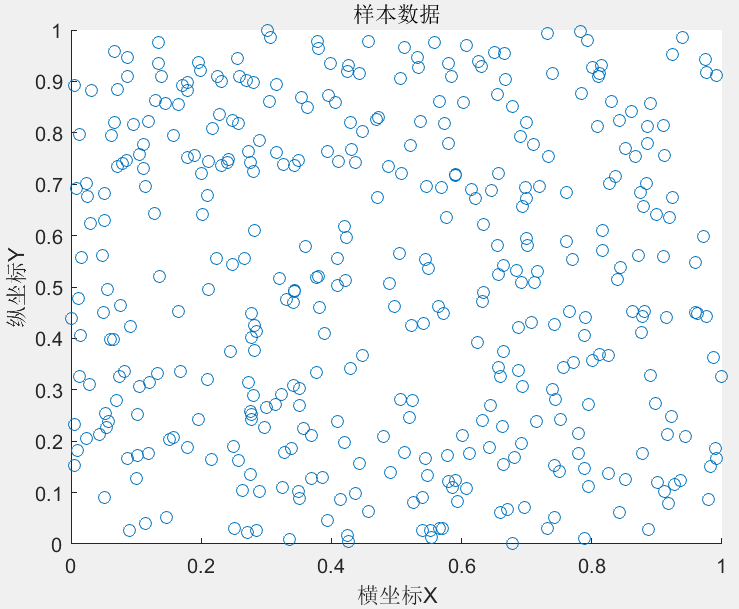
    将SAGA作用于随机产生的数据进行实验。数据由400个二维平面上的点组成，这些点构成4个集合，但彼此之间并没有明显的界限，数据如图1所示。通过使用单纯的FCM聚类和SAGA优化初始聚类中心点后的FCM聚类来说明SAGA优势。

.2 解题思路及步骤

1.模糊C-均值聚类算法(FCM)

    设n个数据样本为X={x1,x2,…,xn}, c(2≤c≤n)是要将数据样本分成的类型的数目，{A1, A2, …, An}表示相应的c个类别，U是其相似分类矩阵，各类别的聚类中心为{v1,v2,…,vc},μk(xi)是样本xi对于类Ak的隶属度(简写为μk)。则目标函数Jb可以用下式表达：

用式(20-3)和式(20-4)反复修改聚类中心、数据隶属度和进行分类，当算法收敛时，理论上就得到了各类的聚类中心以及各个样本对于各模式类的隶属度，从而完成了模糊聚类划分。尽管FCM有很高的搜索速度，但FCM是一种局部搜索算法，且对聚类中心的初值十分敏感，如果初值选择不当，它会收敛到局部极小点。

    2.模拟退火算法实现

    模拟退火算法于1983年成功地应用在组合优化的问题上，其思想是通过模拟高温物体退火过程找到优化问题的全局最优或近似全局最优解。首先产生一个初始解作为当前解，然后在当前解的邻域中，以概率P(T)选择一个非局部最优解，并令这个解再重复下去，从而保证不会陷入局部最优。开始时允许随着参数的调整，目标函数偶尔向增加的方向发展(对应于能量有时上升),以利于跳出局部极小区域。随着假想温度的降低(对应于物体的退火),系统活动性降低，最终以概率1稳定在全局最小区域。模拟退火算法描述如下：

3.遗传算法实现

    遗传算法部分直接使用Sheffield遗传算法工具箱相关函数实现。

    (1)编码方式：遗传聚类算法中，待优化的参数是c个初始聚类中心，这里使用二进制编码，每条染色体由c个聚类中心组成，对于m维的样本向量，待优化的变量数为c×m。假定每个变量使用k位二进制编码，则染色体为长度是c×m×k的二进制码串。

    (2)适应度函数：衡量个体优劣的尺度是适应度函数，其作用类似于自然界中生物适应环境能力的度量。每个个体以式(20-1)得出的Jb为目标函数，Jb越小，个体的适应度值就越高。因此，适应度函数采用排序的适应度分配函数：FintV=ranking(Jb)。

    (3)选择算子：选择算子采用随机遍历抽样(sus)。

    (4)交叉算子：交叉算子采用最简单的单点交叉算子。

    (5)变异算子：以一定概率产生变异基因数，用随机方法选出发生变异的基因。如果所选的基因的编码为1,则变为0;反之则变为1。

    4.算法流程

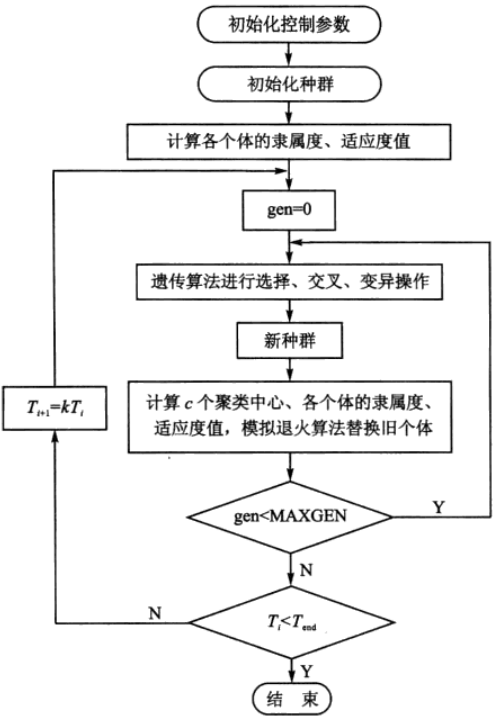
    基于模拟退火遗传算法的模糊C-均值聚类，其过程如图2所示。

4.结果分析

        运行之后得到结果：J,=3.3035,多次运行得到的结果均一致。聚类后的图如图3所示，其中三角形为各类的聚类中心点。

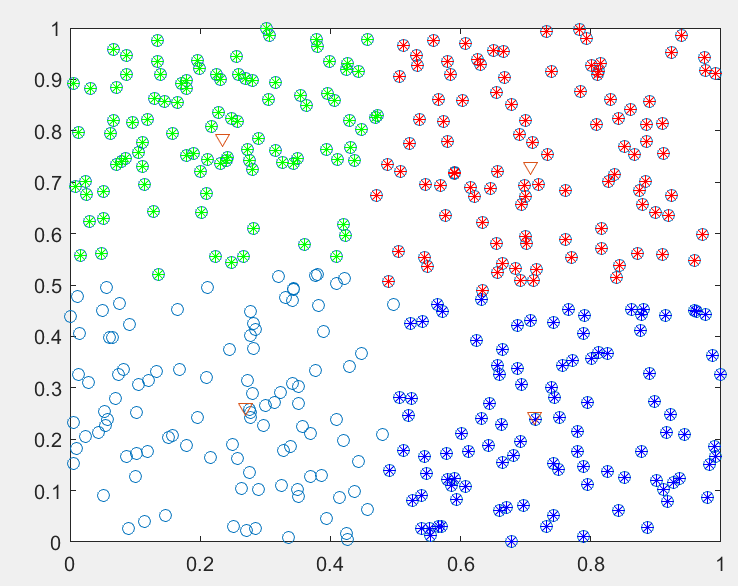
SAGA优化后的FCM聚类Jb=3.3035,每次都能得到最优目标函数值。当数据量较大时，SAGA的优越性更加明显。其主要原因是单纯的FCM在处理大规模数据时，更加容易收敛到局部最优解，而将遗传算法与模拟退火算法相结合形成一种混合算法后，可以有效地克服收敛到局部最优解的情况。

总结

    FCM算法是一种局部搜索优化算法，如果初始值选择不当，它就会收敛到局部极小点上。FCM算法的这一缺点限制了人们对它的使用。本章将模拟退火算法与遗传算法相结合，然后用于模糊C-均值聚类，利用模拟退火算法较强的局部搜索能力和遗传算法较强的全局搜索能力，可以有效、快速地解决聚类问题。