生成式模型和判别式模型的区别_生成式模型与判别式模型的区别

机器学习可以分为两大类：生成式模型（Generative Model）、判别式模型（Discriminative Model）。

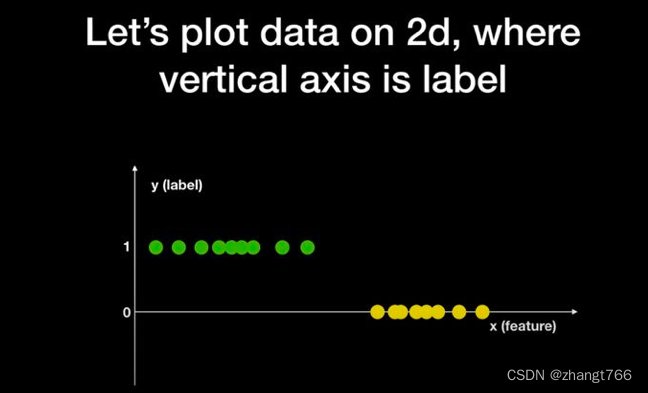
 现在有一堆球，颜色信息已知为绿色和黄色两种，有且仅有这两种颜色，这里，球的颜色为y（目标变量），坐标轴上位置为特征X。我们想要知道，如果在坐标轴的某一位置x新放入一个球，这个球会是什么颜色的？

 1.生成式模型的思想：

 生成式模型使用的是联合概率P(X,Y)，若已知x（球的坐标位置信息），通过计算出P(X,Y)我们就可以知道球的颜色。

 P(X,Y) = P(Y)*P(X|Y)，其中P(Y)可以根据已知球（样本）的颜色分布算出来。

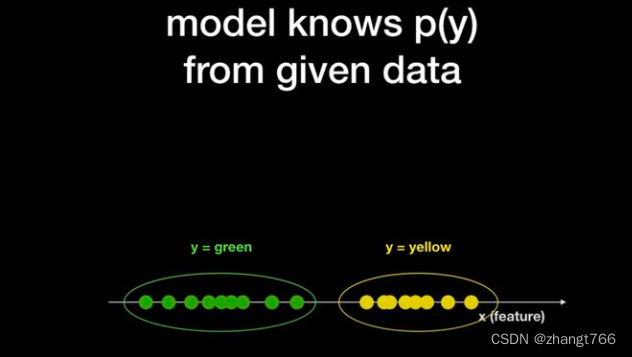
 根据已知样本数据，生成式模型可以估计出Y的分布，见下图橙色曲线。

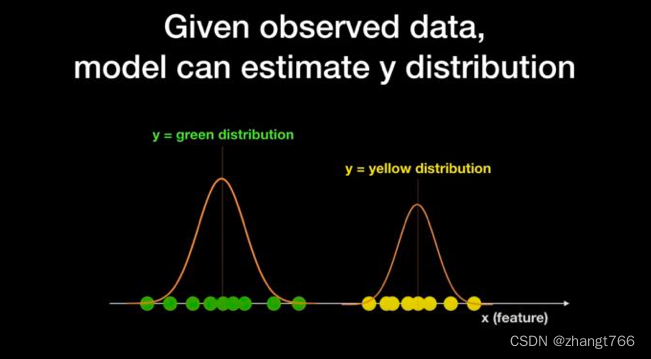
 然后，模型可以算出P(X|Y=green)的值，即当球的颜色是绿色时，球在坐标轴上的各个位置的概率。同理，也可以算出P(X|Y=yellow)。

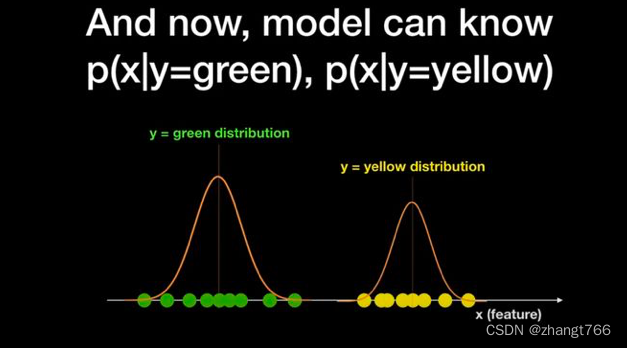
 现在，新给一个球，把它放在坐标轴某个位置上，让我们预测，这个球是绿色的概率大？还是黄色的概率大？

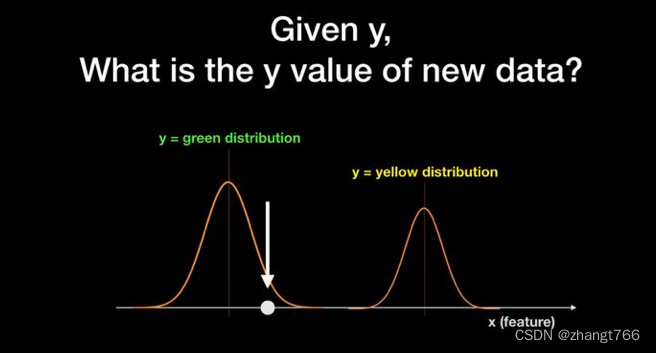
 通过比较联合概率P(X,Y=green)和P(X,Y=yellow)谁更大，我们便能知道新给的球为什么颜色啦~这里，很明显，球对应的分布曲线为y = green的那条，P(X,Y=green)取值是大于0的，而P(X,Y=yellow)取值为0。

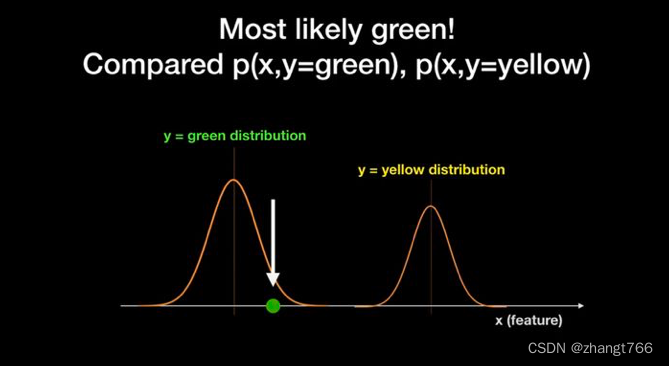
 总结：生成式模型主要通过学习样本，形成多个Y分布，然后计算联合概率P(X,Y)，根据P(X,Y)的值预测新的样本属于哪个类。对于二分类问题，如果P(X,Y1)>P(X,Y2)，则新样本X判定为Y1。

2.判别式模型的思想：

 

 

条件概率分布P(Y|X)可以理解为：在已知某样本的特征为X的条件下，计算该样本类别为类别Y1、Y2、Y3的概率，并选择概率最大的类别为该样本的预测类别。如，已知一个花的花瓣长度(X1)、花瓣宽度(X2)、花瓣颜色(X3)、气味(X4)等特征值，求这多花为鸢尾花、菊花、玫瑰的概率，可以表示为：

①P(Y = ‘鸢尾花’| X1 = 2,X2 = 0.5,X3 = ‘红色’,X4 = ‘无味’)，

②P(Y = ‘菊花’| X1 = 2,X2 = 0.5,X3 = ‘红色’,X4 = ‘无味’)

③P(Y = ‘玫瑰’| X1 = 2,X2 = 0.5,X3 = ‘红色’,X4 = ‘无味’)

计算出来，③的概率值最大，因此将该样本划分为玫瑰。

常见的判别式模型：支持向量机、决策树。

3.生成式模型优缺点

（1）生成式模型的优点：过拟合的几率比较小，尤其是当你采集的数据的分布与真实世界整体数据集的分布是相近的适合，基本上不用担心过拟合问题。

 

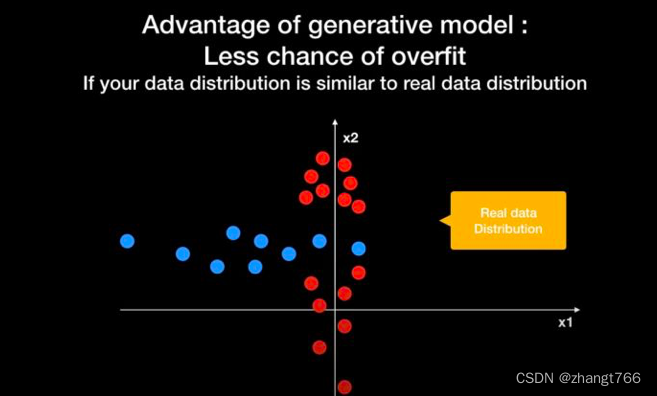
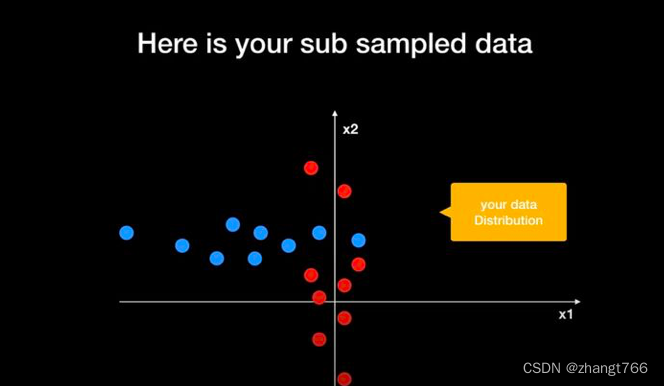
 红色圆圈和蓝色圆圈就是基于样本数据生成的分布函数，如下：

 下面，新给出一些白色小球，需要我们预测这些白色小球应该属于红色还是蓝色？

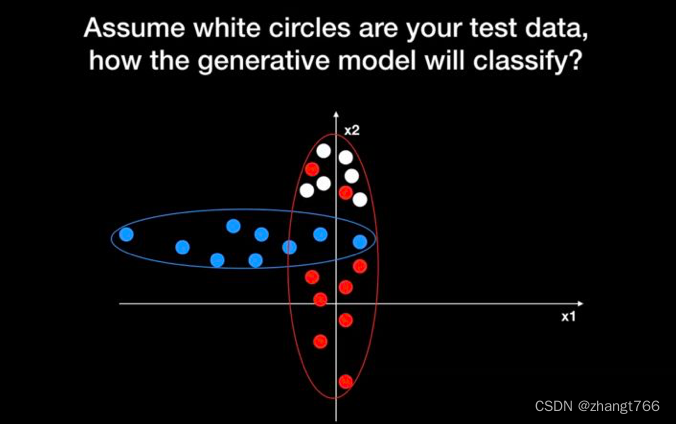
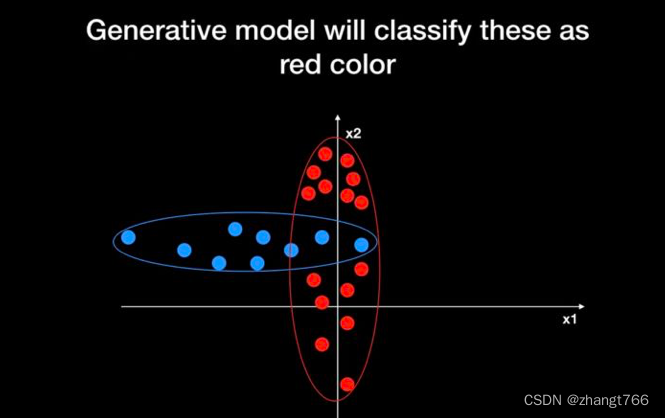
 生成式模型，根据前面得到的y分布，会将白色小球颜色预测为红色，如下：

 判别式模型根据生成的分类边界（绿色那条线）对小球的颜色进行预测：

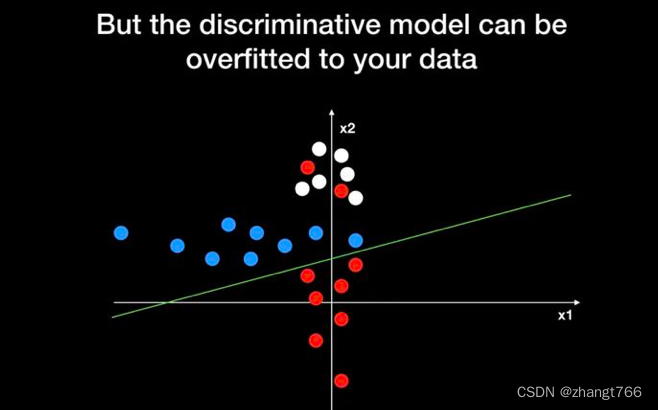
 判别式模型认为，分界线以上的都为蓝色，分界线以下的都为红色，因此，判别式模型分类的准确性高度依赖于分类边界函数的准确性。

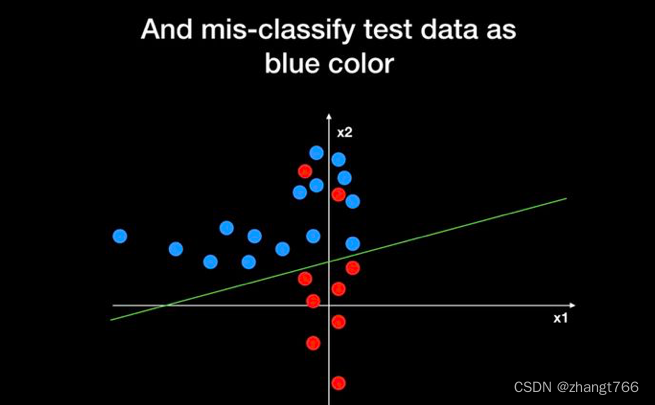
（2）生成式模型的缺点：

因为生成式模型需要生成Y的分布函数，而这个分布函数可能会受到一些异常点的影响变得不那么准确，如下图所示，有两个黄色小球乱入了绿军阵营，有两个绿色小球混进了黄球阵营。

 

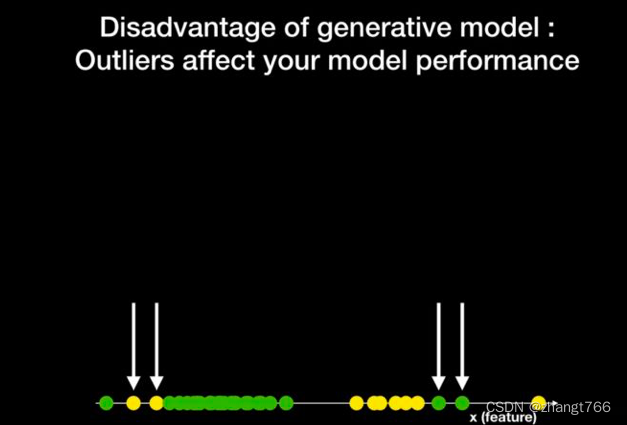
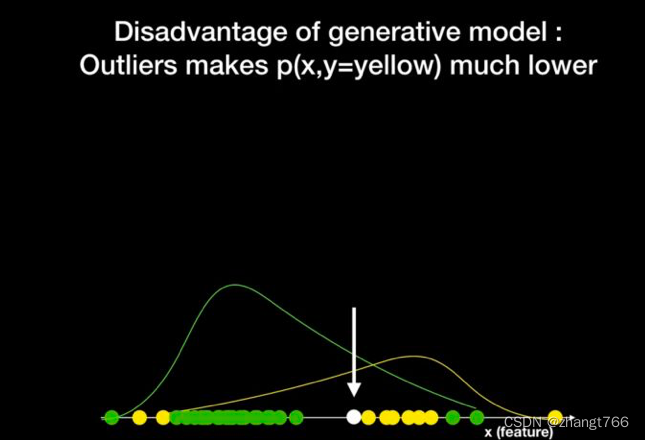
此时，我们得到的Y分布函数如下，可以明显看的分布函数与之前发生了较大变化，绿球的分布函数出现了明显的右倾，而黄球的分布函数出现了明显的左倾：

 

 此时，如下图所示又有一个白色小球，已知它在坐标轴上的位置，需要我们判段它是黄色还是绿色。根据联合概率分布的值来看，白色小球对应的两条分布曲线中，绿色线更高，因此我们就会认为小球属于绿色的概率更大。

 

生成式模型还有两个缺点：

1）为了使生成的分布函数与真实世界中的分布函数尽可能接近，需要大量的数据来生成模型。

2）生成式模型比判别式模型计算量更大。

4.判别式模型的优缺点

（1）优点：在小数据集上表现效果很好，但是要注意过拟合问题。另外，计算量比生成式模型小。