- 1Qt开发笔记:Qt3D三维开发笔记(一):Qt3D三维开发基础概念介绍_使用qt做3维图形显示需要什么技术
- 2git push origin master失败报错“fatal: unable to access...“解决方法_git.exe push --set-upstream --progress "origin" ma
- 3LVGL移植到ARM开发板(GEC6818)_lvgl移植arm
- 4mysql查询包含某两个标签_如何查询同时包含多个指定标签的文章
- 5如何在WooCommerce中设置运费(免费功能)_woocommerce产品价格后添加运费
- 6java split()方法_java split方法
- 7贝锐蒲公英异地组网方案:实现制药设备远程监控、远程运维
- 8Linux系统的网络设置_linux 上网
- 9SCI期刊介绍—IEEE Open Journal of the Communications Society
- 10智慧农业新纪元:解锁新质生产力,加速产业数字化转型
【神经网络+数学】——(4)神经网络求解二元偏微分问题(二阶偏微分)_神经网络解偏微分方程的代码
赞
踩
背景
前面几篇博客介绍了神经网络应用到积分、一元N阶微分的原理、方法并实践了可行性,取得了较好的拟合效果,现在针对偏微分方程PDE进行最后的攻关,完成该部分攻关后即基本掌握了神经网络应用到方程求解的原理方法以及实践代码的自主可控,其实多元N阶微分如果不是偏微分方程则可表示为(以一阶微分为例)
d x d t d y d t + d x d t + d y d t + x ( t ) + y ( t ) + 2 = 0 \frac{dx}{dt}\frac{dy}{dt}+\frac{dx}{dt}+\frac{dy}{dt}+x(t)+y(t)+2=0 dtdxdtdy+dtdx+dtdy+x(t)+y(t)+2=0
该种微分方程可通过两分支输出网络来解决(关键代码如下):
model = Model(inputs=inputs_t,outputs=[outputs_x,outputs_y])
[x,y] = model.predict(t)
loss = sum((x'*y'+x'+y'+x+y+2)**2)
- 1
- 2
- 3
同时在经典的数值方法中,比如有限差分、有限元方法,其刚度矩阵具有稀疏性,但它们的未知数的个数或者网格的节点数随着 PDE 的维度呈指数增长,会出现维数灾难 (Curse of dimensionality, CoD)。谱方法虽然采用了没有紧支集的基函数从而具有指数精度,但是牺牲了稀疏性,而且对函数的光滑性有很高的要求。因而,传统方法在处理高维 PDE 变得特别困难,使用神经网络求解带来了新的思路方法(该部分背景参考知乎)。
问题描述
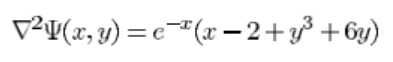
定义域(求解区域) x , y ∈ [ 0 , 1 ] x,y\in[0,1] x,y∈[0,1]
Dirichlet 边界条件:
ψ
(
0
,
y
)
=
y
3
\psi(0,y)=y^3
ψ(0,y)=y3
ψ
(
1
,
y
)
=
(
1
+
y
3
)
e
−
1
\psi(1,y)=(1+y^3)e^{-1}
ψ(1,y)=(1+y3)e−1
ψ
(
x
,
0
)
=
x
e
−
x
\psi(x,0)=xe^{-x}
ψ(x,0)=xe−x
ψ
(
x
,
1
)
=
(
x
+
1
)
e
−
x
\psi(x,1)=(x+1)e^{-x}
ψ(x,1)=(x+1)e−x
用于验证的解析解:
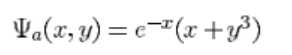
其中拉普拉斯算子
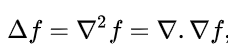
计算公式为非混合的二阶偏导之和:
(1-D情况)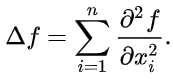
(2-D情况)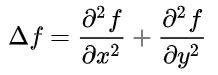
经计算验证,解析解 ψ \psi ψ对x求二阶偏导加上对y求二阶偏导的结果就是原问题等式,所以下面开始进行模型构建和训练验证。
模型搭建
使用tf2+python3.7环境,自动微分的结果表示微分函数值,训练代码如下(不包含net类的定义代码,需要付费获取,请私信联系博主):
# 随机打乱 seed = np.random.randint(0, 2021, 1)[0] input_space_raw = input_space.copy()#save 原序的方便绘曲面图 np.random.seed(seed) np.random.shuffle(input_space) output_space = psy_analytic_np(input_space[:, 0], input_space[:, 1]) input_space = tf.reshape(input_space, (-1, input_space.shape[-1])) input_space = tf.cast(input_space, tf.float32) # 默认是float64会报错不匹配,所以要转类型 net = PDE_Net(input_space, tf.reduce_min(input_space), tf.reduce_max(input_space), w=w, activation=activation) if retrain: net.model_load() optimizer = Adam(lr) for epoch in range(epochs): grad, loss, loss_data, loss_equation, loss_border = net.train_step() optimizer.apply_gradients(zip(grad, net.trainable_variables)) if epoch % 100 == 0: print("loss:{}\tloss_data:{}\tloss_equation:{}\tloss_border:{}\tepoch:{}".format(loss, loss_data, loss_equation, loss_border, epoch)) net.model_save() # plot output_space = psy_analytic_np(input_space_raw[:, 0], input_space_raw[:, 1]) input_space = tf.reshape(input_space_raw, (-1, input_space_raw.shape[-1])) input_space = tf.cast(input_space, tf.float32) predict = net.net_call(input_space).numpy() fig = plt.figure(figsize=(8, 6)) ax = fig.gca(projection='3d') ax.plot_surface(input_space_raw[:, 0].reshape(grid, grid), input_space_raw[:, 1].reshape(grid, grid), output_space.reshape(grid, grid), cmap=cm.rainbow) ax.plot_surface(input_space_raw[:, 0].reshape(grid, grid), input_space_raw[:, 1].reshape(grid, grid), predict.reshape(grid, grid), cmap=cm.ocean) plt.title("predictions curve mixed") plt.show() fig = plt.figure(figsize=(8, 6)) ax = fig.gca(projection='3d') ax.plot_surface(input_space_raw[:, 0].reshape(grid, grid), input_space_raw[:, 1].reshape(grid, grid), predict.reshape(grid, grid), cmap=cm.rainbow) plt.title("predictions curve Pred") plt.show() fig = plt.figure(figsize=(8, 6)) ax = fig.gca(projection='3d') ax.plot_surface(input_space_raw[:, 0].reshape(grid, grid), input_space_raw[:, 1].reshape(grid, grid), output_space.reshape(grid, grid), cmap=cm.rainbow) plt.title("predictions curve True") plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
训练超参配置:
activation = 'tanh'
grid = 10
epochs = 5000
lr = 0.01
w = (1, 1, 0.001)
- 1
- 2
- 3
- 4
- 5
训练两次后:



最后的日志输出:
loss:2.0242910385131836 loss_data:0.07997725158929825 loss_equation:0.01357131078839302 loss_border:1930.742431640625 epoch:4500
loss:2.6815528869628906 loss_data:0.08011103421449661 loss_equation:0.6714369654655457 loss_border:1930.0048828125 epoch:4600
loss:2.022817850112915 loss_data:0.0801229402422905 loss_equation:0.013348560780286789 loss_border:1929.3463134765625 epoch:4700
loss:2.022118330001831 loss_data:0.08013834059238434 loss_equation:0.013231338933110237 loss_border:1928.74853515625 epoch:4800
loss:2.0260419845581055 loss_data:0.07978630065917969 loss_equation:0.016707584261894226 loss_border:1929.548095703125 epoch:4900
model saved in net.weights
- 1
- 2
- 3
- 4
- 5
- 6
反复训练调试,先使用0.00001级别的border loss权重又增大到1,极限训练后:

结论
可见最后两张曲面图近似,说明网络收敛,使用神经网络来求解偏微分方程是可行的,且遵循和求解一元微分方程一样的原理,即通过自动微分来获取方程的各元素,然后利用 l o s s = l o s s d a t a + l o s s e q u a t i o n + l o s s b o r d e r loss = loss_{data} + loss_{equation} + loss_{border} loss=lossdata+lossequation+lossborder 来构造loss用于反向传播更新参数。不过要想把训练精度提上来仍需努力,现阶段收敛所需要的迭代次数太多,100个网格离散点的情况下至少万级的epoch,训练效率很低,而且达到的精度也不是很高。
DGM求解PDE与PINN十分类似。



