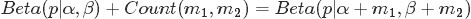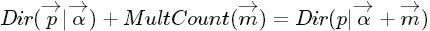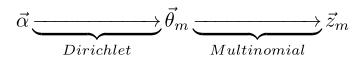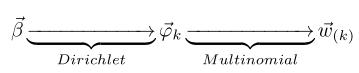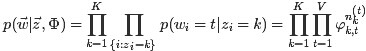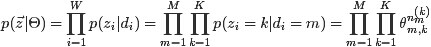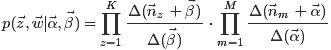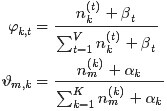- 1linux运维常用命令(持续更新)_linux运维常用的20个命令
- 2在CentOS7上安装Python 3.9教程。_centos7 安装 python3.9
- 3PBKDF2加密_pbkdf在线
- 4推荐文章:Design2Code - 前端自动化的新篇章
- 5exception in thread main org.apache.spark.sparkexception:A master URL must be set in your
- 6粒子群算法讲解以及MATLAB实现_粒子群matlab代码
- 7保研推免经历经验分享——2018北大软微、北航计算机、南大计算机夏令营保研经历_北大软件与微电子学院夏令营与北航计算机学院夏令营录取率
- 8HBase系统架构及数据结构_hbase中最小的操作单元是 cell row key column
- 9初识Docker应用容器引擎 -- 如何优雅的发布web应用
- 10并查集 — Java语言实现_set createset(int size)
主题模型TopicModel:隐含狄利克雷分布LDA_lda主题模型原理介绍隐含狄利克雷分布
赞
踩
主题模型LDA简介
隐含狄利克雷分布简称LDA(Latent Dirichlet allocation),首先由Blei, David M.、吴恩达和Jordan, Michael I于2003年提出,目前在文本挖掘领域包括文本主题识别、文本分类以及文本相似度计算方面都有应用。
LDA是一种典型的词袋模型,即它认为一篇文档是由一组词构成的一个集合,词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
它是一种主题模型,它可以将文档集中每篇文档的主题按照概率分布的形式给出;
同时是一种无监督学习算法,在训练时不需要手工标注的训练集,需要的仅仅是文档集以及指定主题的数量k即可;
此外LDA的另一个优点则是,对于每一个主题均可找出一些词语来描述它;
LDA可以被认为是一种聚类算法:
- 主题对应聚类中心,文档对应数据集中的例子。
- 主题和文档在特征空间中都存在,且特征向量是词频向量。
- LDA不是用传统的距离来衡量一个类簇,它使用的是基于文本文档生成的统计模型的函数。
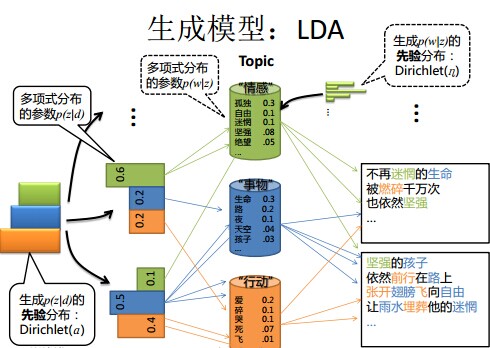
LDA的概率图及生成表示

[LDA automatically assigns topics to text documents]
Note:
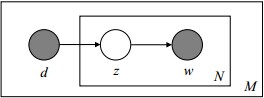
1 阴影圆圈表示可观测的变量,非阴影圆圈表示隐变量;箭头表示两变量间的条件依赖性;方框表示重复抽样,方框右下角的数字代表重复抽样的次数。这种表示方法也叫做plate notation,参考PRML 8.0 Graphical Models。
对应到图2, α⃗ 和 β⃗ 是超参数;方框中, Φ={φ⃗ k} 表示有 K 种“主题-词项”分布; Θ={ϑ⃗ m} 有 M 种“文档-主题”分布,即对每篇文档都会产生一个 ϑ⃗ m 分布;每篇文档 m 中有 n 个词,每个词 wm,n 都有一个主题 zm,n ,该词实际是由 φ⃗ zm,n 产生。
2 φ(topic-word分布) and θ(doc-topic分布) 是狄利克雷分布, z(赋给词w的主题) and w(当前词) 是多项式分布. θ指向z是从doc-topic分布中采样一个主题赋给w(但是此时还不知道词w具体是什么,而是只知道其主题),φ指向w是φ的topic-word分布依赖于w。
LDA生成模型
当我们看到一篇文章后,往往喜欢推测这篇文章是如何生成的,我们可能会认为作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文。LDA就是要根据给定的一篇文档,推测其主题分布。
因此正如LDA贝叶斯网络结构中所描述的,在LDA模型中一篇文档生成的方式如下:
- 从狄利克雷分布
 中取样生成文档i的主题分布
中取样生成文档i的主题分布
- 从主题的多项式分布
 中取样生成文档i第j个词的主题
中取样生成文档i第j个词的主题
- 从狄利克雷分布
 中取样生成主题
中取样生成主题 的词语分布
的词语分布
- 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语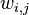
LDA模型参数求解概述
因此整个模型中所有可见变量以及隐藏变量的联合分布是
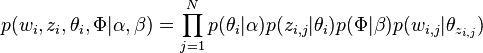 (这里i表示第i个文档)
(这里i表示第i个文档)
最终一篇文档的单词分布的最大似然估计可以通过将上式的 以及
以及 进行积分和对
进行积分和对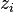 进行求和得到
进行求和得到
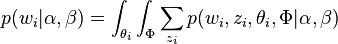
根据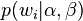 的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
LDA的参数估计(吉布斯采样)
在LDA最初提出的时候,人们使用EM算法进行求解。
后来人们普遍开始使用较为简单的Gibbs Sampling,具体过程如下:
- 首先对所有文档中的所有词遍历一遍,为其都随机分配一个主题,即zm,n=k~Mult(1/K),其中m表示第m篇文档,n表示文档中的第n个词,k表示主题,K表示主题的总数,之后将对应的n(k)m+1, nm+1, n(t)k+1, nk+1, 他们分别表示在m文档中k主题出现的次数,m文档中主题数量的和??(可重复的,所以应该就是文档中词的个数,不变的量)??,k主题对应的t词的次数,k主题对应的总词数(n(k)m等等初始化为0)。
- 之后对下述操作进行重复迭代。
- 对所有文档中的所有词进行遍历,假如当前文档m的词t对应主题为k,则n(k)m-1, nm-1, n(t)k-1, nk-1, 即先拿出当前词,之后根据LDA中topic sample的概率分布采样出新主题,在对应的n(k)m, nm, n(t)k, nk上分别+1。
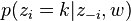 ∝
∝ 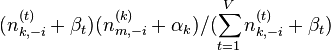 (topic sample的概率分布)
(topic sample的概率分布)
- 迭代完成后输出主题-词参数矩阵φ和文档-主题矩阵θ
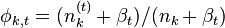 主题k中词t的概率分布
主题k中词t的概率分布
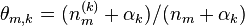 文档m中主题k的概率分布
文档m中主题k的概率分布
从这里看出,gibbs采样方法求解lda最重要的是条件概率p(zi | z-i,w)的计算上。
[http://zh.wikipedia.org/wiki/隐含狄利克雷分布]
LDA中的数学基础
- beta分布是二项式分布的共轭先验概率分布:“对于非负实数
和
,我们有如下关系
其中
对应的是二项分布
的计数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。”
- 狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布:
- “ 把
从整数集合延拓到实数集合,从而得到更一般的表达式如下:
- “ 把
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是 Dirichlet-Multinomial 共轭。 ”
正如Beta分布是二项式分布的共轭先验概率分布,狄利克雷分布作为多项式分布的共轭先验概率分布。
-
贝叶斯派思考问题的固定模式:
- 先验分布
+ 样本信息
后验分布
上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对的认知是先验分布
,在得到新的样本信息
后,人们对
的认知为
。
- 先验分布
- 频率派与贝叶斯派各自不同的思考方式:
- 频率派把需要推断的参数θ看做是固定的未知常数,即概率
虽然未知,但是是确定的一个值,同时样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
- 而贝叶斯派的观点则截然相反,他们认为待估计的参数
是随机变量,服从一定的分布,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数
的分布。
- 频率派把需要推断的参数θ看做是固定的未知常数,即概率
主题模型LDA文档生成模式
理解lda生成词的关键,lz建议先看lda基础模型。当然,已经理解可以直接跳过,看推理参数部分。
[TopicModel - Unigram、LSA、PLSA算法详解]
从LDA与pLSA的区别和联系角度出发
LDA就是在pLSA的基础上加层贝叶斯框架。pLSA样本随机,参数虽未知但固定,属于频率派思想;而LDA样本固定,参数未知但不固定,是个随机变量,服从一定的分布,LDA属于贝叶斯派思想。
pLSA与LDA生成文档方式的对比
pLSA模型按照如下的步骤生成“文档-词项”:
- 按照概率
选择一篇文档
- 选定文档
后,确定文章的主题分布
- 从主题分布中按照概率
选择一个隐含的主题类别
- 选定
后,确定主题下的词分布
- 从词分布中按照概率
选择一个词
LDA模型中一篇文档生成的方式:
- 按照先验概率
选择一篇文档
- 从狄利克雷分布
中取样生成文档
的主题分布
,换言之,主题分布
由超参数为
的Dirichlet分布生成
- 从主题的多项式分布
中取样生成文档
第 j 个词的主题
- 从狄利克雷分布(即Dirichlet分布)
中取样生成主题
对应的词语分布
,换言之,词语分布
由参数为
的Dirichlet分布生成
- 从词语的多项式分布
中采样最终生成词语

从上面两个过程可以看出,LDA在PLSA的基础上,为主题分布和词分布分别加了两个Dirichlet先验(也就是主题分布的分布和词分布的分布)。
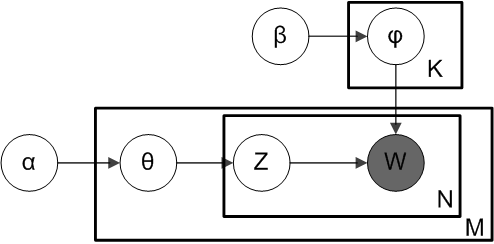
对应到上面右图的LDA,只有W / w是观察到的变量,其他都是隐变量或者参数,其中,Φ表示词分布,Θ表示主题分布,
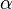 是主题分布Θ的先验分布(即Dirichlet 分布)的参数,
是主题分布Θ的先验分布(即Dirichlet 分布)的参数,
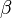 是词分布Φ的先验分布的参数,N表示文档的单词总数,M表示文档的总数。
是词分布Φ的先验分布的参数,N表示文档的单词总数,M表示文档的总数。
- 假定语料库中共有M篇文章,每篇文章下的Topic的主题分布是一个从参数为
的Dirichlet先验分布中采样得到的Multinomial分布,每个Topic下的词分布是一个从参数为
的Dirichlet先验分布中采样得到的Multinomial分布。
- 对于某篇文章中的第n个词,首先从该文章中出现的每个主题的Multinomial分布(主题分布)中选择或采样一个主题,然后再在这个主题对应的词的Multinomial分布(词分布)中选择或采样一个词。不断重复这个随机生成过程,直到M篇文章全部生成完成。
- 其中,
→θ→z 表示生成文档中的所有词对应的主题,显然
→θ 对应的是Dirichlet 分布,θ→z 对应的是 Multinomial 分布,所以整体是一个 Dirichlet-Multinomial 共轭结构,如下图所示:
- 类似的,
→φ→w,容易看出, 此时β→φ对应的是 Dirichlet 分布, φ→w 对应的是 Multinomial 分布, 所以整体也是一个Dirichlet-Multinomial 共轭结构,如下图所示:
pLSA与LDA参数估计方法的对比
- pLSA中,我们使用EM算法去估计“主题-词项”矩阵Φ和“文档-主题”矩阵Θ,而且这两参数都是个未知的固定的值,使用的思想其实就是极大似然估计MLE。
- LDA中,估计Φ、Θ这两未知参数可以用变分(Variational inference)-EM算法,也可以用gibbs采样,前者的思想是最大后验估计MAP(MAP与MLE类似,都把未知参数当作固定的值),后者的思想是贝叶斯估计。贝叶斯估计是对MAP的扩展,但它与MAP有着本质的不同,即贝叶斯估计把待估计的参数看作是服从某种先验分布的随机变量。
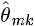 、
、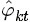 。LDA中,主题分布和词分布本身都是多项分布,而由上文可知“Dirichlet分布是多项式分布的共轭先验概率分布”,因此选择Dirichlet 分布作为它们的共轭先验分布。意味着为多项分布的参数p选取的先验分布是Dirichlet分布,那么以p为参数的多项分布用贝叶斯估计得到的后验分布仍然是Dirichlet分布。
。LDA中,主题分布和词分布本身都是多项分布,而由上文可知“Dirichlet分布是多项式分布的共轭先验概率分布”,因此选择Dirichlet 分布作为它们的共轭先验分布。意味着为多项分布的参数p选取的先验分布是Dirichlet分布,那么以p为参数的多项分布用贝叶斯估计得到的后验分布仍然是Dirichlet分布。
- PLSA中,主题分布和词分布是唯一确定的,能明确的指出主题分布可能就是{教育:0.5,经济:0.3,交通:0.2},词分布可能就是{大学:0.5,老师:0.3,课程:0.2}。
- LDA中,主题分布和词分布不再唯一确定不变,即无法确切给出。例如主题分布可能是{教育:0.5,经济:0.3,交通:0.2},也可能是{教育:0.6,经济:0.2,交通:0.2},到底是哪个我们不再确定,因为它是随机的可变化的。但再怎么变化,也依然服从一定的分布,即主题分布跟词分布由Dirichlet先验随机确定。面对多个主题或词,各个主题或词被抽中的概率不一样,所以抽取主题或词是随机抽取。主题分布和词分布本身也都是不确定的,正因为LDA是PLSA的贝叶斯版本,所以主题分布跟词分布本身由先验知识随机给定。
- pLSA中,主题分布和词分布确定后,以一定的概率(
、
)分别选取具体的主题和词项,生成好文档。而后根据生成好的文档反推其主题分布、词分布时,最终用EM算法(极大似然估计思想)求解出了两个未知但固定的参数的值:
(
)和
(
)
- 举个文档d产生主题z的例子。给定一篇文档d,主题分布是一定的,比如{ P(zi|d), i = 1,2,3 }={0.4,0.5,0.1},表示z1、z2、z3,这3个主题被文档d选中的概率都是个固定的值:P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1。
- 贝叶斯框架下的LDA中,我们不再认为主题分布和词分布是唯一确定的(而是随机变量),而是有很多种可能。LDA为它们弄了两个Dirichlet先验参数,为某篇文档随机抽取出某个主题分布和词分布。
- 文档d产生主题z(准确的说,其实是Dirichlet先验为文档d生成主题分布Θ,然后根据主题分布Θ产生主题z)的概率,主题z产生单词w的概率都不再是某两个确定的值,而是随机变量。
- 例子:给定一篇文档d,现在有多个主题z1、z2、z3,它们的主题分布{ P(zi|d), i = 1,2,3 }可能是{0.4,0.5,0.1},也可能是{0.2,0.2,0.6},即这些主题被d选中的概率都不再认为是确定的值,而主题分布到底是哪个取值集合我们不确定(这就是贝叶斯派的核心思想,把未知参数当作是随机变量,不再认为是某一个确定的值),但其先验分布是dirichlet 分布,所以可以从无穷多个主题分布中按照dirichlet 先验随机抽取出某个主题分布出来。
- 文档d产生主题z(准确的说,其实是Dirichlet先验为文档d生成主题分布Θ,然后根据主题分布Θ产生主题z)的概率,主题z产生单词w的概率都不再是某两个确定的值,而是随机变量。
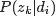 、
、
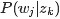 )加了两个先验分布的参数(贝叶斯化):一个主题分布的先验分布Dirichlet分布
)加了两个先验分布的参数(贝叶斯化):一个主题分布的先验分布Dirichlet分布
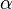 ,和一个词语分布的先验分布Dirichlet分布
,和一个词语分布的先验分布Dirichlet分布
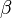 。
。
LDA是pLSA的generalization:一方面LDA的hyperparameter设为特定值的时候,就specialize成pLSA了。从工程应用价值的角度看,这个数学方法的generalization,允许我们用一个训练好的模型解释任何一段文本中的语义。而pLSA只能理解训练文本中的语义。(虽然也有ad hoc的方法让pLSA理解新文本的语义,但是大都效率低,并且并不符合pLSA的数学定义。)
LDA生成文档过程的进一步理解
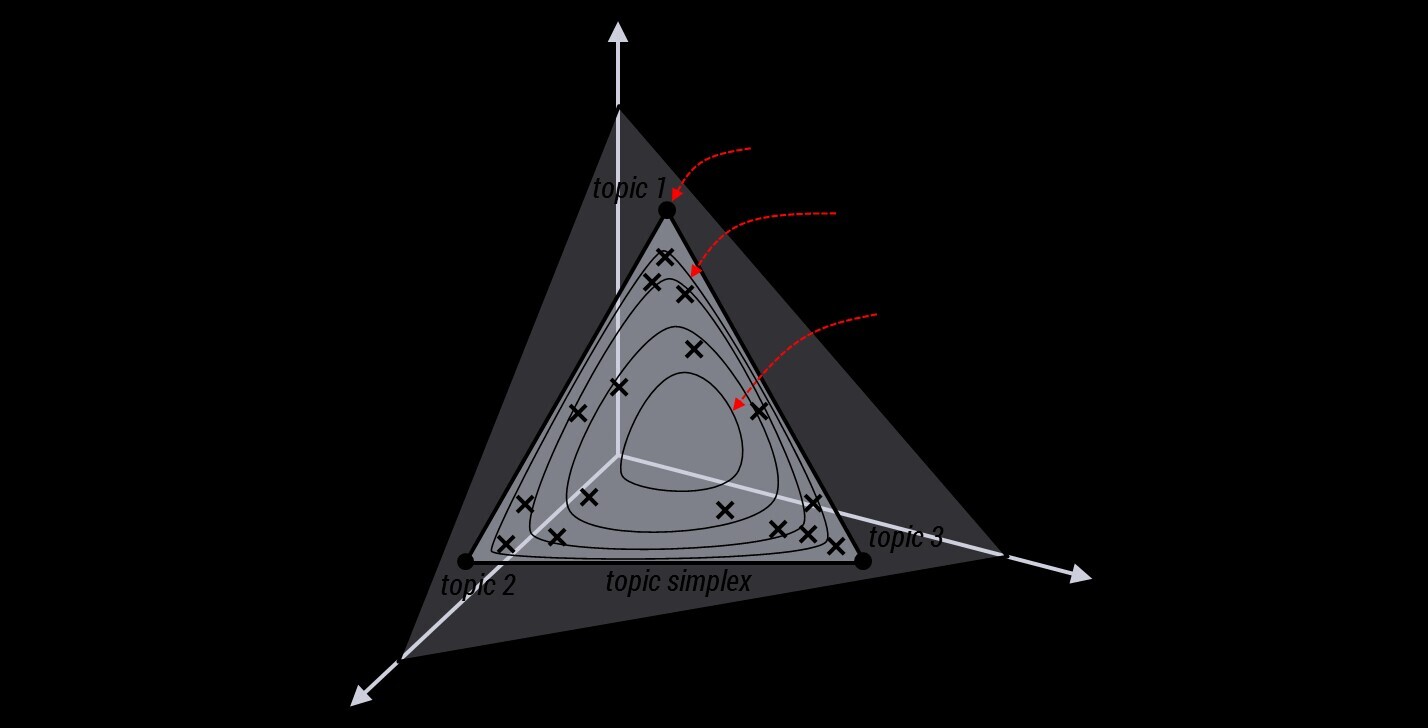
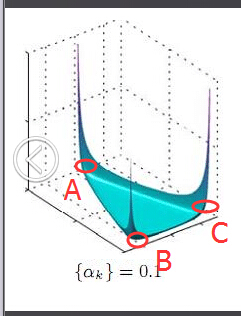
为了说清楚这个问题,咱们得回顾下dirichlet分布。事实上,如果我们取3个事件的话,可以建立一个三维坐标系,类似xyz三维坐标系,这里,我们把3个坐标轴弄为p1、p2、p3,如下图所示:
在这个三维坐标轴所划分的空间里,每一个坐标点(p1,p2,p3)就对应着一个主题分布,且某一个点(p1,p2,p3)的大小表示3个主题z1、z2、z3出现的概率大小(因为各个主题出现的概率和为1,所以p1+p2+p3 = 1 {三角平面},且p1、p2、p3这3个点最大取值为1)。比如(p1,p2,p3) = (0.4,0.5,0.1)便对应着主题分布{ P(zi), i =1,2,3 } = {0.4,0.5,0.1},空间里有很多这样的点(p1,p2,p3),意味着有很多的主题分布可供选择,那dirichlet分布如何选择主题分布呢?把上面的斜三角形放倒,映射到底面的平面上,便得到如下所示的一些彩图(3个彩图中,每一个点对应一个主题分布,高度代表某个主题分布被dirichlet分布选中的概率,且选不同的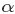
Note:
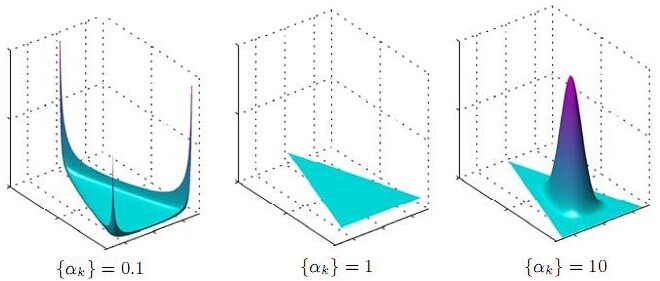
1 上图的绘制大概这样:alpha=0.1固定时,dirichlet分布的概率密度函数就固定了

这个概率密度在x1或x2或x3为1,其余为0时的概率最大,x1=x2=x3时概率最小,也就是上图1所示的了。
2 alpha=0.1到10看出,alpha越大,选出的主题分布越倾向于均匀分布(也就是主题分布是均匀相等的概率最大)。
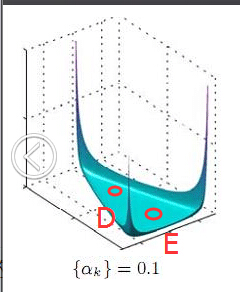
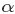 是如何决定dirichlet分布的形状的,可以从dirichlet分布的定义和公式思考。
是如何决定dirichlet分布的形状的,可以从dirichlet分布的定义和公式思考。
LDA参数估计:Gibbs采样
理解这一节,需要先看懂吉布斯采样算法。
类似于pLSA,LDA的原始论文中是用的变分-EM算法估计未知参数,但不太好理解,并且EM算法可能推导出局部最优解。后来发现另一种估计LDA未知参数的方法更好,Heinrich使用了Gibbs抽样法。Gibbs抽样是马尔可夫链蒙特卡尔理论(MCMC)中用来获取一系列近似等于指定多维概率分布(比如2个或者多个随机变量的联合概率分布)观察样本的算法。
LDA Gibbs Sampler
为了构造LDA Gibbs抽样器,我们需要使用隐变量的Gibbs抽样器公式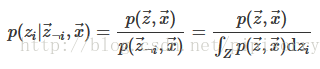
(lz:这里分母实际只是分子对zi的一个积分,将变量zi积分掉,就得到p(z-i, x),所以重点在联合分布p(z,w)公式上,一般先推出联合分布公式再积分就可以使用上面的隐变量gibbs采样公式了。而这个联合分布就是我们采样出来的结果推断出的近似分布,也就是下面LDA所有变量的联合分布如何通过采样结果求解出来)。
在LDA模型中,隐变量为 zm,n ,即样本中每个词 wm,n 所属的主题,而参数 Θ 和 Φ 等可以通过观察到的 wm,n 和相应的 zm,n 积分求得,这种处理方法称作collapsed,在Gibbs sampling中经常使用。
要推断的目标分布p(z|w)(后验概率分布),它和联合分布成正比 {这里省略了超参数},这个分布涉及很多离散随机变量,并且分母是
个项的求和,很难求解(正如从一维均匀分布采样很容易,直接从二维均匀分布采样就比较困难了,也是通过固定某个维度gibbs采样的)。此时,就需要Gibbs sampling发挥用场了,我们期望Gibbs抽样器可以通过Markov链利用全部的条件分布
p(zi|z¬i,w)
来模拟
p(z|w)
。
LDA所有变量的联合分布
联合概率分布 p(w,z) : p(w,z|α,β)=p(w|z,β)p(z|α)
给定一个文档集合,w是可以观察到的已知变量,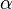 和
和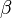 是根据经验给定的先验参数,其他的变量z,θ和φ都是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
是根据经验给定的先验参数,其他的变量z,θ和φ都是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
因为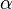
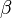
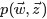
(从概率图表示中也可以看出)
由于此公式第一部分独立于 ,第二部分独立于
,所以可以分别处理。计算的两个未知参数:第一项因子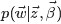
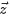
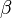
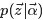
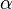
采样词过程
第一个因子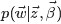
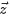
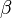
由于样本中的词服从参数为主题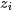
其中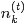
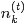
Note:
1 每个主题下包含所有词,所有词都要考虑,只是概率不一样而已。并且这里的w和z上面都有箭头,都是向量。
2 初始时每个词w随机分配主题k,这样每个主题下的词也就随机分配了,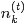
回到第一个因子上来,目标分布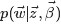
(68)
其中在LDA中的数学模型定义的Dirichlet 分布的归一化系数
的公式
(两种表达方式,其中int表示积分)
这个结果可以看作K个Dirichlet-Multinomial模型的乘积。
Note: 推导:
采样主题过程
类似,对于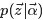
其中,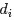
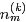
对主题分布Θ积分可得联合分布因子2:
(72)
Note: 上式推导:
综合第一个因子和第二个因子的结果,得到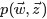
通过联合分布公式就可以得出出下面的条件分布的公式,对每个单词的主题进行采样。
LDA词的主题采样
通过联合分布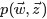 来计算在给定可观测变量 w 下的隐变量 z 的条件分布(后验分布)
来计算在给定可观测变量 w 下的隐变量 z 的条件分布(后验分布)
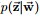 ,再进行贝叶斯分析。换言之,有了这个联合分布后,要求解第m篇文档中的第n个词(下标为
,再进行贝叶斯分析。换言之,有了这个联合分布后,要求解第m篇文档中的第n个词(下标为
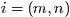 的词)的全部条件概率就好求了。
的词)的全部条件概率就好求了。
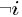 表示除去
表示除去
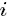 的词,
的词,
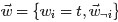 ,
,
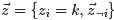

公式(80)
-i除去当前词i相关的不考虑where n−i is the count excluding the current assignment of z i , i.e., z −i .;n−i denotes a quantity excluding the current instance;
z−i代表不是wi的其它所有单词对应的不同主题组成的集合(类似式68中nz的定义)。
n(t)k,-i表示主题k中单词t(除了单词wi外,wi也是词t1,注意不在和式中的t是指wi等于的单词t)的个数;而n(t)k表示主题k中单词t的个数;
给个示例吧


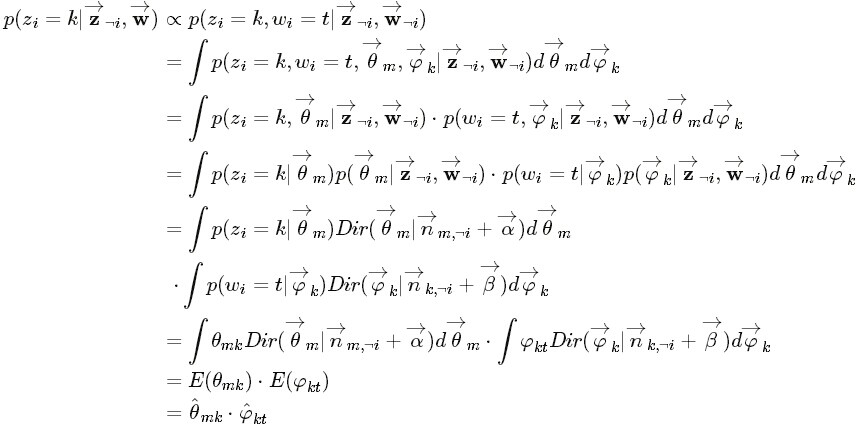 公式(81)
公式(81)
Note:不必使用这个公式进行采样,这个公式只是下面解释LDA吉布斯采样图解过程时比较方便。
这就是罐子模型!richer get richer!

主题分布参数Θ和词分布参数Φ的计算
Note: LDA的原始论文中,主题的词分布通常叫β,但是在许多后来的论文中叫φ,如on smoothing and inference for topic models.
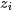 获取主题分布的参数Θ和词分布的参数Φ(知道了每篇文档下每个词对应的主题,那么文档下的主题分布和主题的词分布就好求了)。
获取主题分布的参数Θ和词分布的参数Φ(知道了每篇文档下每个词对应的主题,那么文档下的主题分布和主题的词分布就好求了)。
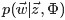 和
和
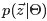 各自被分解成两部分乘积的结果,可以计算得到每个文档上Topic的后验分布和每个Topic下的词的后验分布分别如下(据上文可知:其后验分布跟它们的先验分布一样,也都是Dirichlet 分布):可知,文档m中主题的概率分布是 数据学习得到的主题多项式分布似然*文档m主题分布的Dir先验。
各自被分解成两部分乘积的结果,可以计算得到每个文档上Topic的后验分布和每个Topic下的词的后验分布分别如下(据上文可知:其后验分布跟它们的先验分布一样,也都是Dirichlet 分布):可知,文档m中主题的概率分布是 数据学习得到的主题多项式分布似然*文档m主题分布的Dir先验。
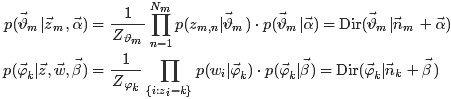
其中,是构成文档m的主题数向量,
是构成主题k的词项数向量。
文档m主题的概率分布公式推导如下:
根据Dirichlet 分布期望,最终得到的分布参数求解公式为(注意分布参数的计算要在sampling收敛阶段进行):
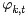 和
和
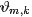 的结果代入之前得到的
的结果代入之前得到的
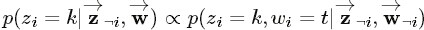 {公式(81)}的结果中,可得:
{公式(81)}的结果中,可得:
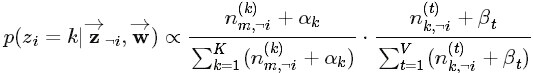
 ,这个概率的值对应着
,这个概率的值对应着
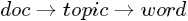 的路径概率。如此,K 个topic 对应着K条路径,Gibbs Sampling 便在这K 条路径中进行采样,如下图所示:
的路径概率。如此,K 个topic 对应着K条路径,Gibbs Sampling 便在这K 条路径中进行采样,如下图所示:
- 算法: LdaGibbs({w,α,β,K})
- 输入:单词向量 w ,超参数 α 和 β ,主题数 K
- 全局变量:统计量 {n(k)m} 、 {n(t)k} ,以及它们的总数 {nm} 、 {nk} ,全部条件概率数组 p(zi|⋅)
- 输出:主题向量 {z} ,多项分布参数 Φ 和 Θ ,超参数估计量 α 和 β
- [初始化] 设置全局变量 n(k)m 、 n(t)k 、 nm 、 nk 为零
-
对所有文档 m∈[1,M] :
- 对文档
m
中的所有单词
n∈[1,Nm]
:
- 采样每个单词对应的主题 zm,n=k∼Mult(1/K)
- 增加“文档-主题”计数: n(k)m+=1
- 增加“文档-主题”总数: nm+=1
- 增加“主题-词项”计数: n(t)k+=1
- 增加“主题-词项”总数: nk+=1
- 对文档
m
中的所有单词
n∈[1,Nm]
:
-
迭代burn-in和sampling步骤:
- [burn-in] 对所有文档
m∈[1,M]
:
- 对文档
m
中的所有单词
n∈[1,Nm]
:
- 减少计数: n(k)m−=1;nm−=1;n(t)k−=1;nk−=1;
- 根据公式p(zi=k|z¬i,w) = ...{公式(80)}采样主题: k∼p(zi|z¬i,w)
- 增加计数: n(k~)m+=1;nm+=1;n(t)k~+=1;nk~+=1;
- 对文档
m
中的所有单词
n∈[1,Nm]
:
- [sampling] 如果Markov链收敛:
- 根据公式φk,t生成参数 Φ
- 根据公式ϑm,k生成参数 Θ
- [burn-in] 对所有文档
m∈[1,M]
:
[参数估计方法Gregor Heinrich.Parameter estimation for text analysis* - 5.5 The collapsed LDA Gibbs sampler]
LDA算法评价
推断算法复杂度
LDA inference is O(kN2) where N is the number of words, and k is the number of topics.
from:http://blog.csdn.net/pipisorry/article/details/42649657
ref: [Blei, David; Ng, Andrew;Latent Dirichlet allocation.Journal of Machine Learning Research*]
[David M. Blei《Introduction to Probabilistic Topic Models》译文:概率主题模型简介 Introduction to Probabilistic Topic Models]
[主题模型之LDA*]
[LDA学习笔记---来自《Parameter estimation for text analysis》]