第十届蓝桥杯C/C++省赛研究生组

试题A：立方和（5分）

题目代码

#include<iostream>
using namespace std;
bool judge(int num)
{
	while (num)//如何获取各个位的值
	{
		int t = num % 10;
		if (t == 2 || t == 0 || t == 1 || t == 9)
		{
			return true;
		}
		num /= 10;
	}
	return false;
}

int main()
{
	long long int sum = 0;
	for (double i = 1; i <= 2019; i++)//注意溢出问题，int会溢出，改用double类型
	{
		if (judge(i))
		{
			sum += i * i * i;
		}
	}
	cout << sum << endl;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

题目答案：4097482414389

---

试题B：字串数字（5分）

题目分析

二十六进制转化为十进制，要使用long long 类型。
注意：快速幂算法

题目代码

#include<iostream>
#include<string>
#include<map>
using namespace std;
typedef long long ll;
map<char, ll>mp;//map容器 前一个代表下标的类型，后一个代表里面值的类型
ll fastpow(ll a, ll n)//快速幂算法，a的n次方
{
	ll base = a;
	ll power = n;
	ll result = 1;
	while (power)
	{
		if (power & 1)//位运算判断奇偶性，若n为偶数则返回0
		{
			result = result * base;//如果指数为奇数,把指数为奇数时分离出来的底数的一次方收集好
		}
		base = base * base;//底数变大成原来的平方
		power >>= 1;//此处等价于power=power/2
	}
	return result;
}
int main()
{
	ll ans = 0;
	char start = 'A';//初始化
	for (ll i = 1; i <= 26; i++)
	{
		mp[start] = i;//把A-Z变为1-26
		start++;
	}
	string s;
	s = "LANQIAO";
	ll len = s.length();
	for (ll i = 0; i < len; i++)
	{
		ans = ans + mp[s[i]] * fastpow(26, len - i - 1);
	}
	printf("%lld\n", ans);//%lld,long long 整型
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

题目答案：3725573269

试题C：质数（10分）

题目代码

#include<iostream>
using namespace std;
bool isprime(int n)//判断是否为质数
{
	for (int i = 2; i < n; i++)
	{
		if (n % i == 0)
		{
			return false;
		}
	}
	return true;
}
int main()
{
	int cnt = 0;
	for (int i = 2; ; i++)
	{
		if (isprime(i))
		{
			cnt++;
		}
		if (cnt == 2019)
		{
			cout << i << endl;
			break;
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

题目答案

17569

---

试题D：最短路（10分）

题目分析

直接数的，动态规划，倒着数

题目答案

6（不知道对不对）

---

试题E：RSA解密（15分）

题目分析

十分难。。
参考资料：解题报告
拓展欧几里得
快速幂算法

题目代码

//求出p，q
#include<cstdio>
typedef long long ll;
int main()
{
	ll res= 1001733993063167141;
	for (ll i = 2; i * i < res; i++)
	{
		if (res % i == 0)
		{
			printf("%lld%  lld\n", i, res / i);//p = 891234941,q = 1123984201
		}
	}
	return 0;
}
求y
#include<cstdio>
int main()
{
	long long y1 = 891234940;
	long long y2 = 1123984200;
	long long y = y1 * y2;
	printf("%lld\n", y);//y = 1001733991047948000
}
扩展欧几里得求e
#include<cstdio>
typedef long long ll;
void exgcd(ll a, ll b, ll& d, ll& x, ll& y)//d is gcd(a,b) 
{
	if (b == 0)
	{
		d = a; x = 1; y = 0;
		return;
	}
	exgcd(b, a % b, d, y, x);
	y -= (a / b) * x;//回溯
}
ll rev(ll t, ll m)
{
	ll d, x, y;
	exgcd(t, m, d, x, y);
	return (x % m + m) % m;
}
int main()
{
	ll y = 1001733991047948000;
	ll d = 212353;
	ll e = rev(d, y);
	printf("%lld\n", e);//e = 823816093931522017
	return 0;
}
快速乘和快速幂
#include<cstdio>
typedef long long ll;
ll fast_product(ll a, ll b, ll mod)
{
	ll ans = 0;
	while (b)
	{
		if (b & 1)
		{
			ans = (ans + a) % mod;
		}
		a = (a + a) % mod;
		b >>= 1;
	}
	return ans;
}
ll fast_pow(ll a, ll b, ll mod)
{
	ll ans = 1;
	while (b)
	{
		if (b & 1)
		{
			ans = fast_product(ans, a, mod);
		}
		a = fast_product(a, a, mod);
		b >>= 1;
	}
	return ans;
}
int main()
{
	ll c = 20190324;
	ll e = 823816093931522017;
	ll n = 1001733993063167141;
	ll answer = fast_pow(c, e, n);
	printf("%lld\n", answer);
	return 0;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

题目答案

579706994112328949

---

试题F：Fibonacci数列与黄金分割（15分）

题目代码

#include<cstdio>
//注意n=20以后，后面的值都相同
long long f[1000];
int main()
{
	f[1] = 1;
	f[2] = 1;
	for (int i = 3; i < 50; i++)
	{
		f[i] = f[i - 1] + f[i - 2];
	}
	int N;
	scanf_s("%d", &N);
	float ans = 0;
	if (N <= 20)
	{
		ans = f[N] * 1.0 / f[N + 1];
	}
	else
	{
		ans = f[20] * 1.0 / f[21];
	}
	printf("%.8f\n", ans);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

试题G：扫地机器人

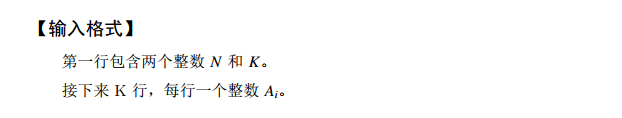
题目代码

扫地机器人二分+贪心
易懂

---

试题H：修改数组（20分）

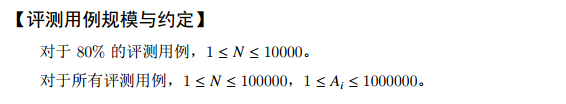
题目分析

并查集

题目代码

#include<iostream>
using namespace std;
//直接暴力会超时，所以使用并查集
const int N = 1000010;
int p[N];
//并查集找到没有出现过的父集
int find(int x)
{
	if (p[x] != x)
	{
		p[x] = find(p[x]);
	}
	return p[x];
}
int main()
{
	for (int i = 0; i < N; i++)
	{
		p[i] = i;
	}
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int x;
		cin >> x;
		x = find(x);
		if (i < n)
		{
			cout << x << " ";
		}
		else
		{
			cout << x << endl;
		}
		p[x] = x + 1;
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

---

试题I：灵能传输（25分）

题目代码

灵能传输

---

试题J：空间跳跃（25分）

题目代码

空间跳跃