大话卷积神经网络CNN（干货满满）

声明：

1）该文章整理自网上的大牛和机器学习专家无私奉献的资料，具体引用的资料请看参考文献。
2）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除。
3）博主才疏学浅，文中如有不当之处，请各位指出，共同进步，谢谢。
4）此属于第一版本，若有错误，还需继续修正与增删。还望大家多多指点。大家都共享一点点，一起为祖国科研的推进添砖加瓦。

O、前言

本博客创作的主要目的，是对时下最火最流行的深度学习算法的基础知识做一个简介，本人看过许多教程，感觉对小白不是特别友好，尤其是在踩过好多坑之后，于是便有了写这篇博客的想法。本文文中会有相关部分的链接，并且在博客的最后会给出 个人推荐的学习资源，如果着急寻找资源的同学可以通过目录直接跳到最后。

一、简介

百度百科中对深度学习的定义是深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向，它被引入机器学习使其更接近于最初的目标——人工智能(AI, Artificial Intelligence)。这个定义太大了，反而让人有点不懂，简答来说，深度学习就是通过多层神经网络上运用各种机器学习算法学习样本数据的内在规律和表示层次，从而实现各种任务的算法集合。各种任务都是啥，有：数据挖掘，计算机视觉，语音识别，自然语言处理等。

可能有人会问那么深度学习，机器学习还有人工智能的关系是怎么样的呢？在这个博客中有详细介绍：一篇文章看懂人工智能、机器学习和深度学习，我们这里直接拿出结论：

• AI：让机器展现出人类智力
• 机器学习：抵达AI目标的一条路径
• 深度学习：实现机器学习的技术

深度学习从大类上可以归入神经网络，不过在具体实现上有许多变化，并不像大家听到的一样，觉得这两个概念其实是同一个东西，在知乎上有相关讨论：看“深度学习”和“多层神经网络”的区别?，我们这里直接拿出结论：

• 从广义上说深度学习的网络结构也是多层神经网络的一种。更简单来说，多层神经网络 做的步骤是：特征映射到值。特征是 人工 挑选。深度学习 做的步骤是 信号->特征->值。 特征是由 网络自己 选择。

深度学习的核心是 特征学习，旨在通过分层网络获取分层次的特征信息，从而解决以往需要人工设计特征的重要难题。深度学习是一个框架，包含多个重要算法：

• Convolutional Neural Networks(CNN)卷积神经网络
• AutoEncoder自动编码器
• Sparse Coding稀疏编码
• Restricted Boltzmann Machine(RBM)限制波尔兹曼机
• Deep Belief Networks(DBN)深度信念网络
• Recurrent neural Network(RNN)多层反馈循环神经网络神经网络

对不同的任务(图像，语音，文本)，需要选用不同的网络模型才能达到更好的效果。

此外，最近几年 增强学习(Reinforcement Learning) 与深度学习的结合也创造了许多了不起的成果，AlphaGo就是其中之一。

大家比较关注的热点新闻，如下图所示：

图片来源：https://zhuanlan.zhihu.com/p/20893777?refer=intelligentunit

二、人类视觉原理

深度学习的许多研究成果，离不开对大脑认知原理的研究，尤其是视觉原理的研究。

1981 年的诺贝尔医学奖，颁发给了 David Hubel（出生于加拿大的美国神经生物学家） 和TorstenWiesel，以及 Roger Sperry。前两位的主要贡献，是“发现了视觉系统的信息处理”——可视皮层是分级的。如下图所示：

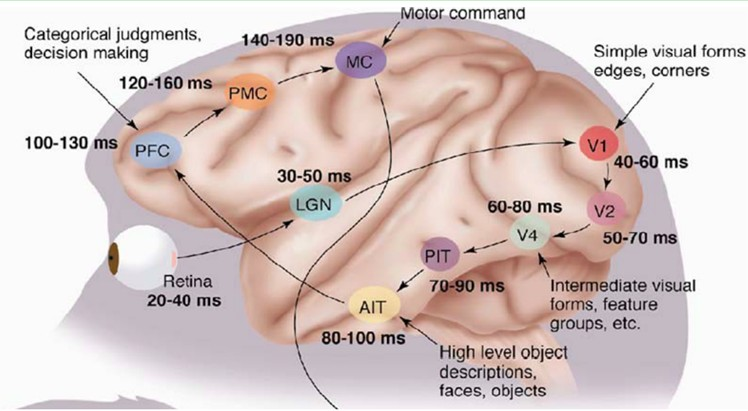
进而通过大量试验研究，发现了人类的视觉原理，具体如下：从原始信号 摄入 开始（瞳孔摄入像素 Pixels），接着做 初步处理（大脑皮层某些细胞发现边缘和方向），然后 抽象（大脑判定，眼前的物体的形状，是圆形的），然后 进一步抽象（大脑进一步判定该物体是只气球）。

下面是人脑进行人脸识别的一个示例。如下图所示：

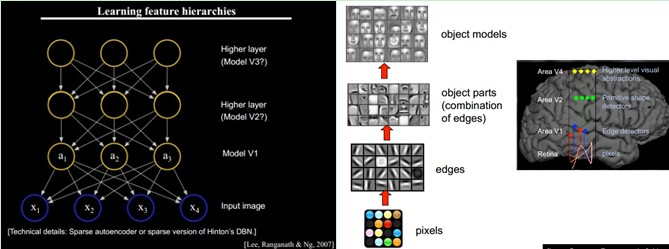
总的来说，人的视觉系统的信息处理是 分级 的。从低级的V1区 提取边缘特征，再到V2区的 形状或者目标的部分 等，再到更高层，整个目标、目标的行为 等。也就是说高层的特征是低层特征的组合，从低层到高层的特征表示越来越抽象，越来越能表现语义或者意图。而抽象层面越高，存在的可能猜测就越少，就越利于分类。

对于不同的物体，人类视觉也是通过这样 逐层分级，来进行认知的。如下图所示：

那么可以很自然的想到：可以不可以模仿人类大脑的这个特点，构造多层的神经网络，较低层的识别初级的图像特征，若干底层特征组成更上一层特征，最终通过多个层级的组合，最终在顶层做出分类呢？答案是肯定的，这也是许多深度学习算法（包括CNN）的灵感来源。

三、神经网络

首先什么是神经网络呢？神经网络也指的是 人工神经网络（Artificial Neural Networks，简称ANNs），是一种模仿生物神经网络行为特征的算法数学模型，由 神经元、节点与节点之间的连接（突触） 所构成，如下图所示：

每个神经网络单元抽象出来的数学模型如下，也叫 感知器，它接收多个输入（$x_1，x_2，x_3...$），产生一个输出，这就好比是神经末梢感受各种外部环境的变化（外部刺激），然后产生电信号，以便于转导到神经细胞（又叫神经元）。如下图所示：

单个的感知器就构成了一个简单的模型，但在现实世界中，实际的决策模型则要复杂得多，往往是由多个感知器组成的多层网络，如下图所示，这也是经典的神经网络模型，由 输入层、隐含层、输出层 构成。如下图所示：

人工神经网络可以映射任意复杂的非线性关系，具有很强的鲁棒性、记忆能力、自学习等能力，在分类、预测、模式识别等方面有着广泛的应用。

四、卷积神经网络

4.1、CNN定义

主角登场，其他人退让！！！如下图所示：

重点来了，什么是卷积神经网络？

百度百科中的定义是 卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一，擅长处理图像特别是图像识别等相关机器学习问题。

卷积网络通过一系列方法，成功将数据量庞大的图像识别问题不断降维，最终使其能够被训练。

4.2、卷积(Convolution)

卷积神经网络中的核心即为 卷积运算，其相当于图像处理中的 滤波器运算。对于一个 $m\times n$ 大小的卷积核，

其对某一原图像 $X$ 进行卷积运算的过程为：卷积核 $W$ 中的每一个权值 $w$ 分别和覆盖的原图像 $X$ 中所对应的像素 $x$ 相乘，然后再求和。计算公式为：

所以一幅图像的一个完整的卷积运算过程为：卷积核以一定的间隔滑动，并对所覆盖的区域进行卷积运算得到值 z，直至遍历完整幅图像。如下图所示：

举一个标准的卷积运算例子，初始位置的计算过程是：1x1+1x0+1x1+0x0+1x1+1x0+0x1+0x0+1x1=4，详细的就不推导了。

如上图，卷积核大小是3x3的，也就是说其卷积核每次覆盖原图像的9个像素，行和列都滑动了3次，一共滑动3x3=9次，得到了一个 $3\times 3$ 的二维数据。这个大小是怎么计算的呢？

首先给出结论，对于一个大小为 $n$ 的原图像，经过大小为 $f$ 的卷积运算后，其输出图像的尺寸为 $n-f+1$。所以对于上图的例子，5-3+1=3即为所求。

4.3、步长（stride）

滑动一定的间距，但这个间距该如何定义呢? 这个概念就是卷积的 “步长”（stride）。经过步长 $s$ 的操作后，其输出图像的尺寸为：

$$\lfloor \frac{n-f}{s}\rfloor +1$$

其中 n 是图像大小，f 是卷积核大小，s 是步长。

stride = 1 表示卷积核滑过每一个相距是 1 的像素，是最基本的单步滑动，作为标准卷积模式。Stride 是 2 表示卷积核的移动步长是 2，跳过相邻像素，输出图像缩小为原来的 1/2。Stride 是 3 表示卷积核的移动步长是 3，跳过 2 个相邻像素，图像缩小为原来的 1/3，以此类推。。。

详细的卷积层尺寸推算细节可以看一下这个文章——CNN中卷积层的计算细节

4.4、填充（padding）

在标准的卷积过程中，存在两个问题：

• 每次卷积运算后，图像就会缩小尺寸。在经历多次运算后，图像最终会失去其本来的形状，变为 $1\times 1$ 的 “柱状”。
• 对于图像边缘的像素，只被一个输出使用，但图像中间的像素，则被多个输出使用。这意味着卷积过程丢掉了图像边缘位置的许多信息。

对于这个问题，可以采用额外的 “假” 像素（通常值为 0， 因此经常使用的术语 ”零填充“ ）填充边缘。这样，在滑动时的卷积核可以允许原始边缘像素位于其中心，同时延伸到边缘之外的假像素。假设填充的像素大小为 $p$ ，则 $n$ 就变成了 $n+2p$，故其输出图像的尺寸为 $\lfloor \frac{n+2p-f}{s}\rfloor +1$。

至于是否选择填充像素，通常有两个选择，分别叫做 Valid 卷积和 Same 卷积。

• Valid 卷积意味着 不填充，即图像会通过卷积并逐渐缩小，输出的图像尺寸即为上述公式：$\lfloor \frac{n+2p-f}{s}\rfloor +1$。
• Same卷积意味 填充，输出图像的尺寸与输入图像的尺寸相同。

根据上述尺寸的计算公式，令 $\lfloor \frac{n+2p-f}{s}\rfloor +1=n$，可得到 $p=\frac{(n-1)s-n+f}{2}$。当 s=1 时，$p=\frac{f-1}{2}$。

4.5、池化(Pooling)

随着模型网络不断加深，卷积核越来越多，要训练的参数还是很多，而且直接拿卷积核提取的特征直接训练也容易出现过拟合的现象。CNN使用的另一个有效的工具被称为“池化(Pooling)”出现并解决了上面这些问题，为了有效地减少计算量，池化就是将输入图像进行缩小，减少像素信息，只保留重要信息；为了有效地解决过拟合问题，池化可以减少数据，但特征的统计属性仍能够描述图像，而由于降低了数据维度，可以有效地避免过拟合。

给出池化的定义，对不同位置区域提取出有代表性的特征（进行聚合统计，例如最大值、平均值等），这种聚合的操作就叫做 池化，池化的过程通常也被称为 特征映射 的过程（特征降维）。听起来很高深，其实简单地说就是下采样。

池化的过程如下图所示：

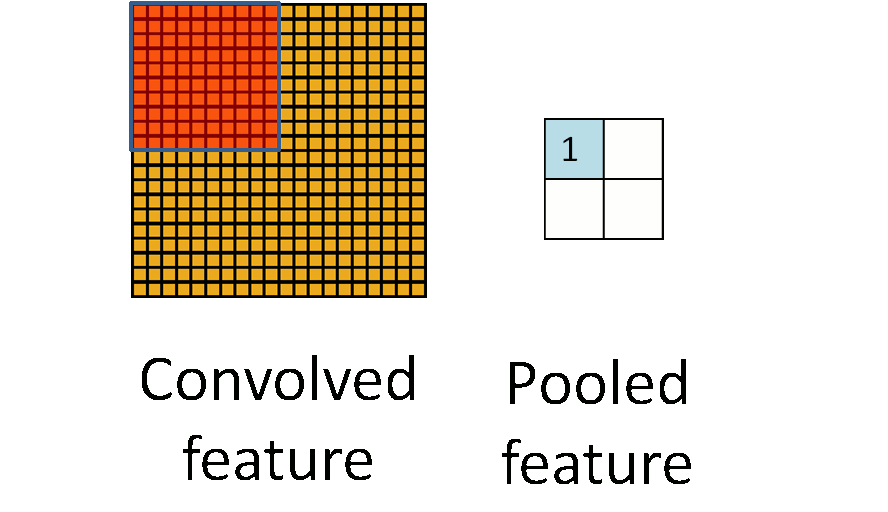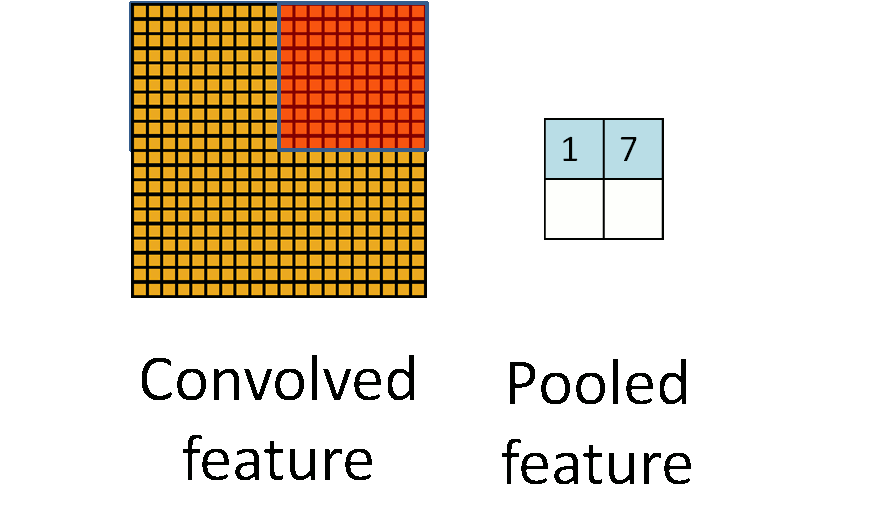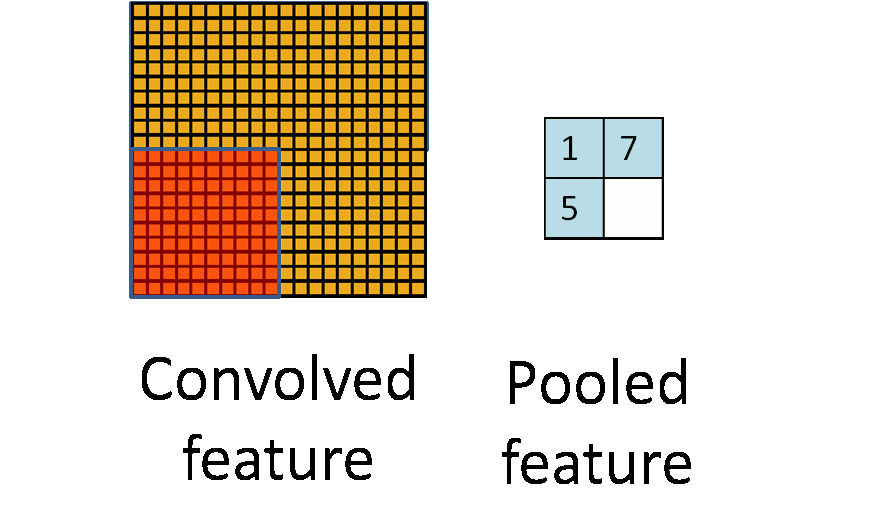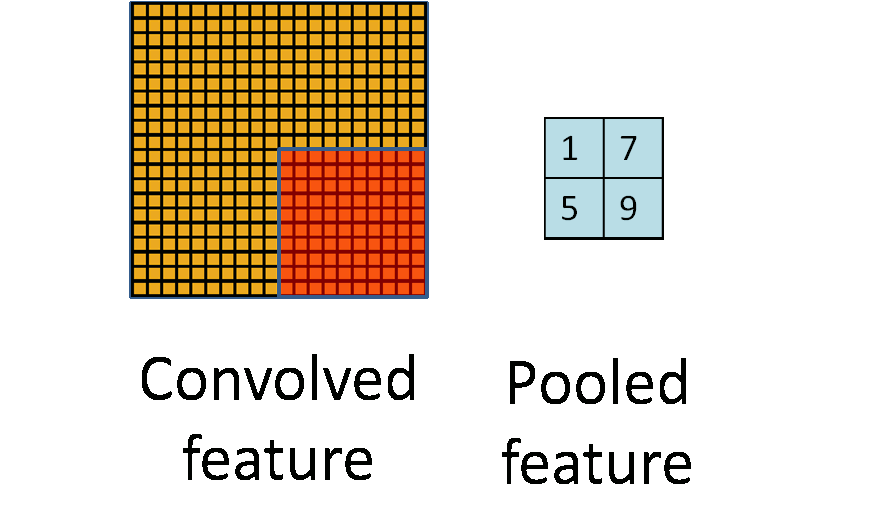
池化主要有两种，除了 最大值池化（Max Pooling） 之外，还有 平均值池化（Average pooling），CNN中随机池化使用的较少。

最大池化是对局部的值取最大；平均池化是对局部的值取平均；随机池化是根据概率对局部的值进行采样，采样结果便是池化结果。概念非常容易理解，其示意图如下所示：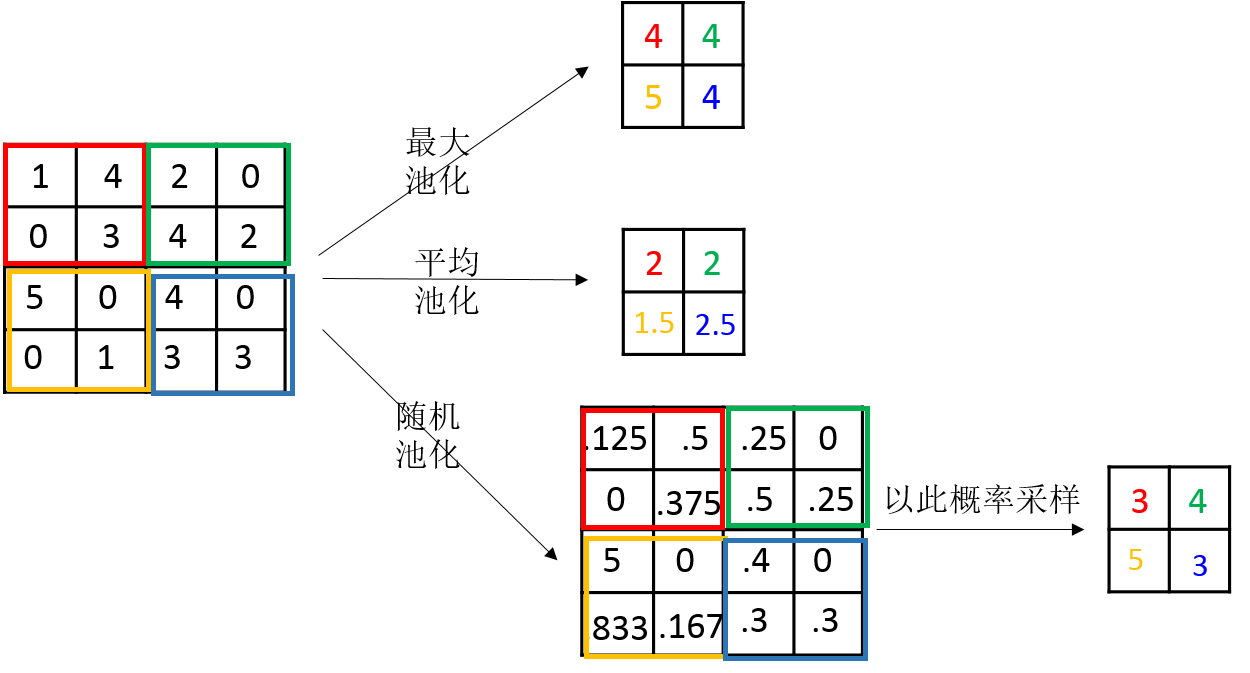
三种池化的意义:

• 最大池化可以获取局部信息，可以更好保留纹理上的特征。如果不用观察物体在图片中的具体位置，只关心其是否出现，则使用最大池化效果比较好。
• 平均池化往往能保留整体数据的特征，能凸出背景的信息。
• 随机池化中元素值大的被选中的概率也大，但不是像最大池化总是取最大值。随机池化一方面最大化地保证了Max值的取值，一方面又确保了不会完全是max值起作用，造成过度失真。除此之外，其可以在一定程度上避免过拟合。

4.6、激活函数

回顾一下感知机，感知机在接收到各个输入，然后进行求和，再经过激活函数后输出。为什么神经网络需要非线性激活函数？

为了使神经网络能够拟合出各种复杂的函数，必须使用 非线性激活函数，用来加入非线性因素，把卷积层输出结果做非线性映射。

在神经网络的正向传播过程中$（Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}，A^{[l]}=g(Z^{[l]})）$，如果我们去掉激活函数 $g$，则 $A^{[l]}=Z^{[l]}$，这个有时被叫做 线性激活函数（更学术点的名字是 恒等激励函数，因为它们就是把输入值恒等地输出），具体公式如下：

第一层：$A^{[1]}=Z^{[1]}=W^{[1]}X+b^{[1]}$

第二层：$A^{[2]}=Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}$

将 $A^{[1]}$ 带入可得第二层：$A^{[2]}=Z^{[2]}=W^{[2]}(W^{[1]}X+b^{[1]})+b^{[2]}=W^{[2]}{W}^{[1]}X+W^{[2]}{b}^{[1]}+b^{[2]}$，令 $W^{[2]}{W}^{[1]}=W^{{}^{\prime }}$，$W^{[2]}{b}^{[1]}+b^{[2]}=b^{{}^{\prime }}$，则第二层变为：$A^{[2]}=Z^{[2]}=W^{{}^{\prime }}X+b^{{}^{\prime }}$。

依此类推，网络的输出仅仅只是输入特征的线性组合。实际上，无论网络有多少层，整体完全可以仅使用1层表示。同理，引入其他线性函数 （如 $g^{{}^{\prime }}=2x$）仍然起不到任何作用，因为线性函数的组合本身仍是线性函数。

常用的激活函数有sigmoid、tanh、relu等等，前两者sigmoid / tanh比较常见于全连接层，后者ReLU常见于卷积层。

4.7、局部感知

为什么要采用局部感知呢？因为可以降低参数量级。为什么要降低参数量级呢？因为如果采用经典的神经网络模型，如下图所示：

则需要读取整幅图像作为神经网络模型的输入（即全连接的方式），当图像的尺寸越大时，其连接的参数将变得很多，从而导致计算量非常大。比如对于一张1000x1000像素的图片，如果我们有1M隐藏层单元，那么一共有 $10^{1}2$ 个参数，这显然是不能接受的。如下图所示：

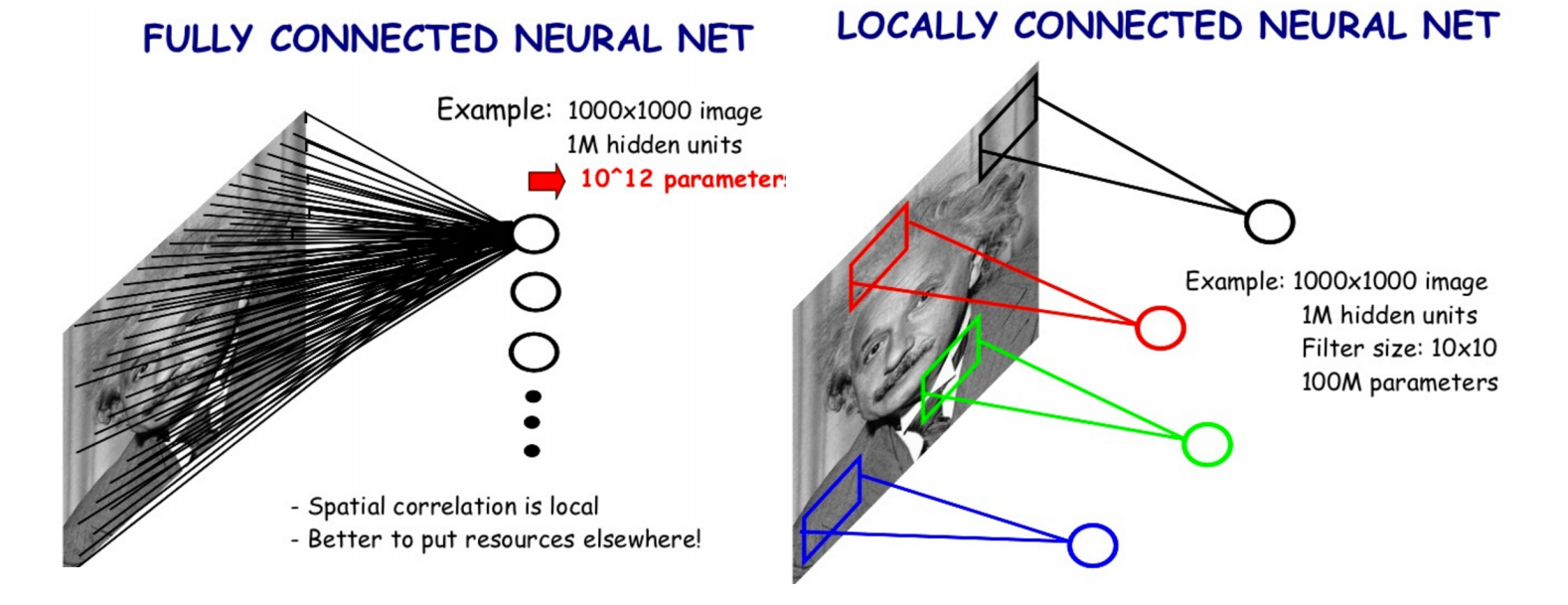
而人类对外界的认知一般是从局部到全局、从片面到全面，先对局部有感知的认识，再逐步对全体有认知，这是人类的认识模式。类似的，在机器识别图像时也没有必要把整张图像按像素全部都连接到神经网络中，局部范围内的像素之间联系较为紧密，而距离较远的像素则 相关性较弱。因而，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息。这种模式就是卷积神经网络中降低参数数目的重要神器：局部感受野，节省了内存。

4.8、参数（权值）共享

每张自然图像（人物、山水、建筑等）都有其固有特性，也就是说，图像其中一部分的统计特性与其它部分是接近的。这也意味着这一部分学习的特征也能用在另一部分上。因此，在局部连接中隐藏层的每一个神经元连接的局部图像的权值参数（例如5×5），将这些 权值参数共享 给其它剩下的神经元使用，那么此时不管隐藏层有多少个神经元，需要训练的参数就是这个局部图像的权限参数（例如5×5），也就是卷积核的大小，这样大大减少了训练参数。如下图所示：

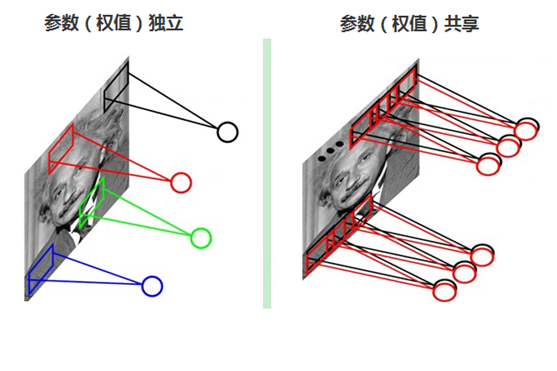
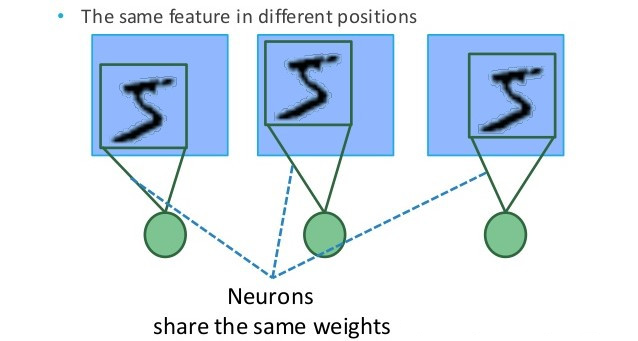
举个例子，假设使用某一特征过滤器（检测器）提取 “手写5” 的特征，那么图片的右下角区域，以及旁边的各个区域都可以使用这个过滤器。每个特征检测器以及输出都可以在输入图片的不同区域中使用同样的参数，以便提取特征 “5”。而对于全连接网络来说，如果模式出现在新的位置，它只能重新学习这个模式。这使得卷积神经网络在处理图像时可以高效利用数据（因为视觉世界从根本上具有 平移不变性），只需要更少的训练样本就可以学到具有泛化能力的数据表示。

4.9、感受野（Receptive field）

感受野用来表示网络内部的不同神经元对原图像的感受范围的大小，换句话说，即为每一层输出的特征图(feature map)上的像素点在原始图像上映射的区域大小。

神经元之所以无法对原始图像的所有信息进行感知，是因为在这些网络结构中普遍使用卷积层和pooling层，在层与层之间均为局部连接。神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着它可能蕴含更为全局，语义层次更高的特征；相反，值越小则表示其所包含的特征越趋向局部和细节。因此感受野的值可以用来大致判断每一层的抽象层次。

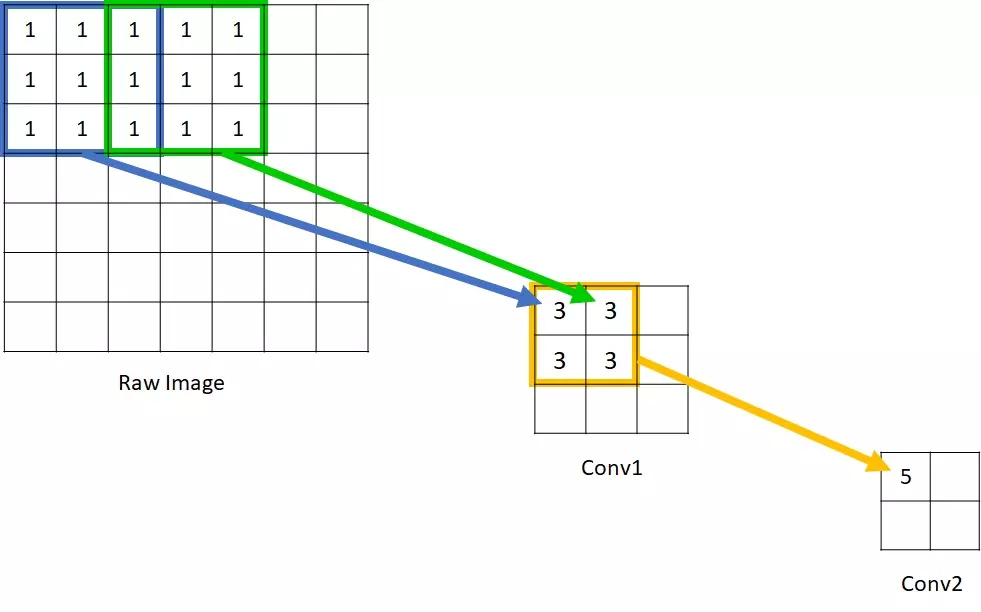
可以看到在Conv1中的每一个单元所能看到的原始图像范围是33，而由于Conv2的每个单元都是由 22范围的Conv1构成，因此回溯到原始图像，其实是能够看到5*5的原始图像范围的。因此我们说Conv1的感受野是3，Conv2的感受野是5。输入图像的每个单元的感受野被定义为1，这应该很好理解，因为每个像素只能看到自己。

五、可视化

学习前的卷积核是随机进行初始化的，使用截断的正态分布或者其他的，所以在黑白的浓淡上没有规律可循，但学习后的滤波器变成了有规律的图像。可以发现，通过学习滤波器被更新成了有规律的滤波器，比如从白到黑渐变的滤波器、含有块状区域（称为blob）的滤波器等。

不同卷积核经过学习，改变了自身对不同特征的响应程度，如边缘（颜色变化的分界线）和斑块（局部的块状区域）等，其中第2个卷积核对垂直边缘响应，第5个卷积核对水平边缘响应，第9个对倾斜边缘响应，第13个对中心斑块响应。

上面的结果是针对第1层的卷积层得出的。第1层的卷积层中提取了边缘或斑块等“低级”信息，而在堆叠了多层的CNN中，随着层次加深，提取的信息（准确说，是响应强烈的神经元））也越来越抽象。如图6.2所示，第1层的神经元对边缘或斑块有响应，第3层对纹理有响应，第5层对物体部件有响应，最后的全连接层对物体的类别（狗或车）有响应。

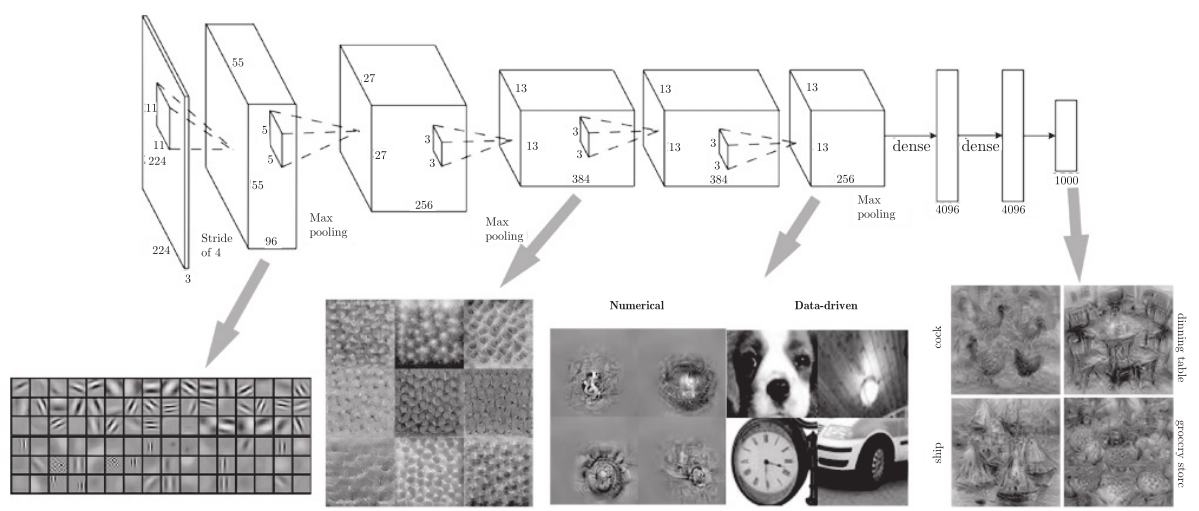
也就是说，随着层次加深，神经元从简单的形状向“高级”信息变化。换句话说，就像我们理解东西的“含义”一样，响应的对象在逐渐变化。

六、应用

CNN 最早 由Yann LeCun提出并应用在 手写字体识别上（MINST）。

当年美国大多数银行就是用它来识别支票上面的手写数字的。能够达到这种商用的地步，它的准确性可想而知。毕竟目前学术界和工业界的结合是最受争议的。LeCun提出的网络称为LeNet5（效果和paper等的链接在这），其网络结构如下：

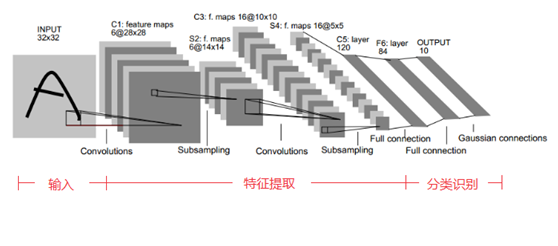
这是一个最典型的卷积网络，由卷积层、池化层、全连接层组成，通过巧妙的设计，利用卷积、参数共享、池化等操作 提取特征，避免了大量的计算成本，最后再使用全连接神经网络进行 分类识别，这个网络也是最近大量神经网络架构的起点，给这个领域带来了许多灵感。

详细的论文讲解，可以查看这个博客——大话CNN经典模型：LeNet

可视化的结果：

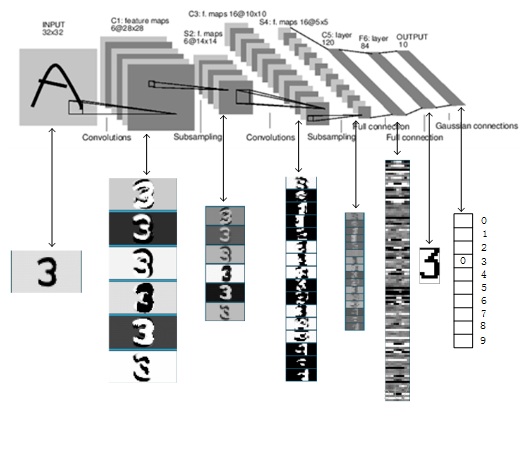
七、深度学习的本质

在Hinton对深层网络做Pre-Train开始就是一个 经验领先于理论分析的偏经验 的一门学问，所以很多人戏称为 黑盒子。那么深度学习的本质到底是什么呢？

我个人更偏向于这种说法——本质就是高维特征变换器，理论上可以做到任意非线性变换。神经网络在坐标系变换的同时，也顺便充当了信息过滤器。

详细的可以看一下这个博客——深度学习的本质

八、境界

深度学习目前处于风口，于是很多人想要浑水摸鱼，都来分一杯羹，然而可能很多人连深度学习是什么都不知道。所以很多人在自学的时候，又不知道从何学起。下了一堆资料，跑了一堆demo，报了一堆cousera，调调参，看看模型结果不错，就以为入了门，抱歉，可能你连门都没入。深度学习这块，有几个层次：

转自一个很厉害的小姐姐的博客三个月教你从零入门深度学习

• demo侠：下载了目前所有流行的框架，对不同框里的例子都跑一跑，看看结果，觉得不错就行了，进而觉得，嘛，深度学习也不过如此嘛，没有多难啊。在面试的时候经常可以遇到不少，很多学生或者刚转行的上来就是讲一个demo，手写数字识别，cifar10数据的图像分类等等，然而你问他这个手写数字识别的具体过程如何实现的？现在效果是不是目前做好的，可以再优化一下吗？为什么激活函数要选这个，可以选别的吗？CNN的原理能简单讲讲吗？懵逼了。

• 调参侠：此类人可能不局限于跑了几个demo，对于模型里的参数也做了一些调整，不管调的好不好，先试了再说，每个都试一下，学习率调大了准确率下降了，那就调小一点，那个参数不知道啥意思，随便改一下值测一下准确率吧。这是大多数初级深度学习工程师的现状。当然，并不是这样不好，对于demo侠来说，已经进步了不少了，起码有思考。然而如果你问，你调整的这个参数为什么会对模型的准确率带来这些影响，这个参数调大调小对结果又会有哪些影响，就又是一问三不知了。

• 懂原理侠：抱歉起了个这么蠢的名字。但是，进阶到这一步，已经可以算是入门了，可以找一份能养活自己的工作了。CNN，RNN，LSTM信手拈来，原理讲的溜的飞起，对于不同的参数对模型的影响也是说的有理有据，然而，如果你要问，你可以手动写一个CNN吗？不用调包，实现一个最基础的网络结构即可，又gg了。

• 懂原理+能改模型细节侠：如果你到了这一步，恭喜你，入门了。对于任何一个做机器学习/深度学习的人来说，只懂原理是远远不够的，因为公司不是招你来做研究员的，来了就要干活，干活就要落地。既然要落地，那就对于每一个你熟悉的，常见的模型能够自己手动写代码运行出来，这样对于公司的一些业务，可以对模型进行适当的调整和改动，来适应不同的业务场景。这也是大多数一二线公司的工程师们的现状。然而，对于模型的整体架构能力，超大数据的分布式运行能力，方案设计可能还有所欠缺。

• 超大数据操控侠：到这一阶段，基本上开始考虑超大数据的分布式运行方案，对整体架构有一个宏观的了解，对不同的框架也能指点一二。海量数据的分布式运行如何避免网络通信的延迟，如何更高效更迅速的训练都有一定经验。这类人，一般就是上一个的领导了。

• 模型/框架架构师：前面说了一堆都是对现有的框架/模型处理的经验，这个阶段的大侠，哦，不对，是大师可以独立设计开发一套新框架/算法来应对现有的业务场景，或者解决一直未解决的历史遗留问题。没啥好说了，膜拜！

有的童鞋会好奇博主是啥水平，实话实说了吧，我也就是个 半斤八两的懂原理侠。。。希望毕业能称为一个 懂原理+能改模型细节侠，哈哈，暂时没啥大目标。

九、学习资源

9.1、编程

首推Python这门编程语言。

1. Python安装：

Python安装包，推荐下载Anaconda，Anaconda是一个用于科学计算的Python发行版，支持 Linux, Mac, Windows系统，提供了包管理与环境管理的功能，可以很方便地解决多版本Python并存、切换以及各种第三方包安装问题。

下载地址：https://www.anaconda.com/download/

IDE：推荐使用pycharm，社区版免费

下载地址：https://www.jetbrains.com/

安装教程：

• Anaconda+Jupyter notebook+Pycharm：https://blog.csdn.net/TeFuirnever/article/details/90646020

• Ubuntu18.04深度学习环境配置(CUDA9+CUDNN7.4+TensorFlow1.8)：https://zhuanlan.zhihu.com/p/50302396

2. python入门的资料推荐

廖雪峰python学习笔记：https://blog.csdn.net/datawhale/article/category/7779959

看完这个资料后python基本达到入门水平。

9.2、理论

这绝对是深度学习入门的首选课程，没有之一！即便你没有扎实的概率论、线性代数等数学基础，也能轻松上手这门深度学习入门课，并体会到无穷趣味。

课程地址：https://mooc.study.163.com/university/deeplearning_ai#/c

9.3、框架

当今深度学习框架有很多，主流的是Google的TensorFlow、Facebook的pytorch还有百度的paddlepaddle，其他的也可以学，这东西多多益善，初学者建议TensorFlow，容易理解一下。

• TensorFlow中文社区
• 深度学习之30分钟快速入门PyTorch（附学习资源推荐）
• paddlepaddle中文社区

9.4、论文

推荐这个大博主的正例论文资源——https://blog.csdn.net/zouxy09/article/details/8782018

十、神经网络游乐场

网站地址：http://playground.tensorflow.org/#activation=relu&batchSize=10&dataset=circle&regDataset=reg-plane&learningRate=0.03&regularizationRate=0&noise=0&networkShape=4,2&seed=0.17410&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false

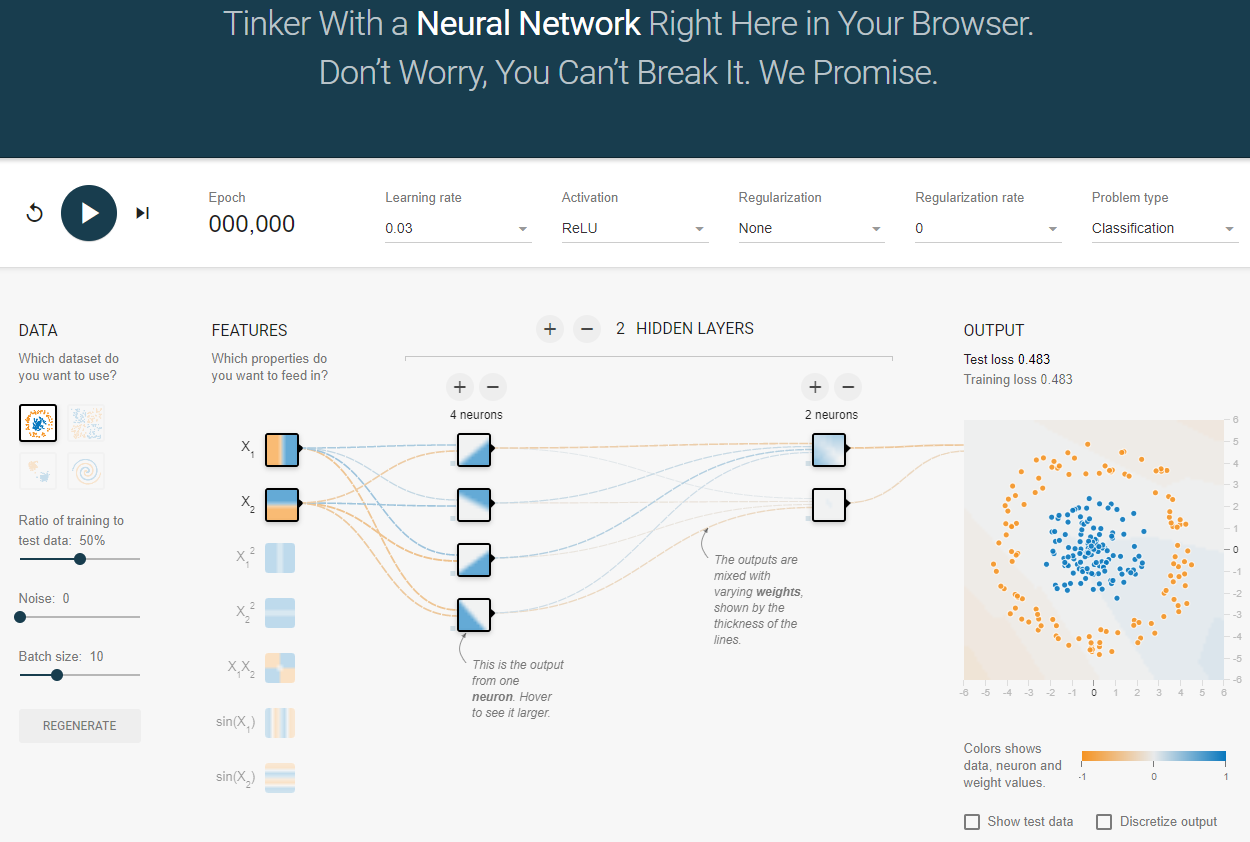
可以调整：

• 数据分布，训练集和测试集的比例，有无噪声，批大小；
• 特征，神经元个数和层数；
• 学习率，激活函数，正则化与否以及大小，分类还是回归。

你可以尝试去改变相应的参数，从而感受一下网络输出的变化，进而体会到卷积神经网络的乐趣，加油！！！

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~

回复【福利】即可获取我为你准备的大礼，包括C++，编程四大件，NLP，深度学习等等的资料。

想看更多文（段）章（子），欢迎关注微信公众号「程序员管小亮」~

十一、参考文章

• 百度百科——深度学习
• 一篇文章看懂人工智能、机器学习和深度学习
• “深度学习”和“多层神经网络”的区别?
• 深度学习简介(一)——卷积神经网络
• Deep Learning（深度学习）学习笔记整理系列之（一）
• 大话卷积神经网络（CNN）
• 百度百科——卷积神经网络
• 大话CNN经典模型：LeNet
• 卷积神经网络概述
• [CNN] 卷积、反卷积、池化、反池化
• Receptive field(感受野)
• 深度学习的本质
• 三个月教你从零入门深度学习