- 1ChatGLM3-6B实践_chatglm3-6b int4 所需算力
- 2Haproxy搭建 Web群集(理论+实操)
- 3深入解析 Jackson 的 @JsonProperty 注解
- 4ubuntu20.04深度学习环境配置(自用基本转载)
- 5蓝桥杯--幸运数_蓝桥杯幸运数
- 6西门子1200PLC与威纶触摸屏多工位转盘博图程序案例,包含程控电源modbus通讯、西门子伺服PN通讯、台达伺服脉冲控制等_西门子plc与威纶通触摸屏通讯
- 7HbuilderX报错“Error: Fail to open IDE“,以及运行之后没有打开微信开发者,或者运行没有反应的解决办法
- 8大模型入门指南(非常详细)零基础入门到精通,收藏这一篇就够了_大模型开发需要什么基础
- 92018年阿里巴巴关于java重要开源项目汇总_阿里巴巴openjdk
- 10LDA(主题模型)_lda主题模型 怎么调参数
动态规划求最大字段和问题_动态规划法求最大子段和问题
赞
踩
1、最大子段和问题
问题定义:对于给定序列a1,a2,a3……an,寻找它的某个连续子段,使得其和最大。如( -2,11,-4,13,-5,-2 )最大子段是{ 11,-4,13 }其和为20。
(1)枚举法求解
枚举法思路如下:
以a[0]开始: {a[0]}, {a[0],a[1]},{a[0],a[1],a[2]}……{a[0],a[1],……a[n]}共n个
以a[1]开始: {a[1]}, {a[1],a[2]},{a[1],a[2],a[3]}……{a[1],a[2],……a[n]}共n-1个
……
以a[n]开始:{a[n]}共1个
一共(n+1)*n/2个连续子段,使用枚举,那么应该可以得到以下算法:
具体代码如下:
-
//3d4-1 最大子段和问题的简单算法 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSum(int n,int *a,int& besti,int& bestj); -
int main() -
{ -
int a[] = {-2,11,-4,13,-5,-2}; -
for(int i=0; i<6; i++) -
{ -
cout<<a[i]<<" "; -
} -
int besti,bestj; -
cout<<endl; -
cout<<"数组a的最大连续子段和为:a["<<besti<<":"<<bestj<<"]:"<<MaxSum(6,a,besti,bestj)<<endl; -
return 0; -
} -
int MaxSum(int n,int *a,int& besti,int& bestj) -
{ -
int sum = 0; -
for(int i=0; i<n; i++)//控制求和起始项 -
{ -
for(int j=i; j<n; j++)//控制求和结束项 -
{ -
int thissum = 0; -
for(int k=i; k<=j; k++)//求和 -
{ -
thissum += a[k]; -
} -
if(thissum>sum)//求最大子段和 -
{ -
sum = thissum; -
besti = i; -
bestj = j; -
} -
} -
} -
return sum; -
}
从这个算法的三个for循环可以看出,它所需要的计算时间是O(n^3)。事实上,如果注意到 ,则可将算法中的最后一个for循环省去,避免重复计算,从而使算法得以改进。改进后的代码如下:
,则可将算法中的最后一个for循环省去,避免重复计算,从而使算法得以改进。改进后的代码如下:
-
//3d4-2 最大子段和问题的避免重复的简单算法 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSum(int n,int *a,int& besti,int& bestj); -
int main() -
{ -
int a[] = {-2,11,-4,13,-5,-2}; -
for(int i=0; i<6; i++) -
{ -
cout<<a[i]<<" "; -
} -
int besti,bestj; -
cout<<endl; -
cout<<"数组a的最大连续子段和为:a["<<besti<<":"<<bestj<<"]:"<<MaxSum(6,a,besti,bestj)<<endl; -
return 0; -
} -
int MaxSum(int n,int *a,int& besti,int& bestj) -
{ -
int sum = 0; -
for(int i=0; i<n; i++)//控制求和起始项 -
{ -
int thissum = 0; -
for(int j=i; j<=n; j++)//控制求和结束项 -
{ -
thissum += a[j];//求和 -
if(thissum>sum) -
{ -
sum = thissum; -
besti = i; -
bestj = j; -
} -
} -
} -
return sum; -
}
(2)分治法求解
分治法思路如下:
将序列a[1:n]分成长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大字段和,则a[1:n]的最大子段和有三中情形:
[1]、a[1:n]的最大子段和与a[1:n/2]的最大子段和相同;
[2]、a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同;
[3]、a[1:n]的最大字段和为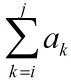 ,且1<=i<=n/2,n/2+1<=j<=n。
,且1<=i<=n/2,n/2+1<=j<=n。
可用递归方法求得情形[1],[2]。对于情形[3],可以看出a[n/2]与a[n/2+1]在最优子序列中。因此可以在a[1:n/2]中计算出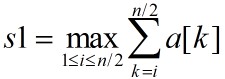 ,并在a[n/2+1:n]中计算出
,并在a[n/2+1:n]中计算出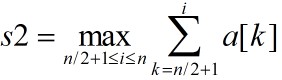 。则s1+s2即为出现情形[3]时的最优值。
。则s1+s2即为出现情形[3]时的最优值。
具体代码如下:
-
//3d4-1 最大子段和问题的分治算法 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSubSum(int *a,int left,int right); -
int MaxSum(int n,int *a); -
int main() -
{ -
int a[] = {-2,11,-4,13,-5,-2}; -
for(int i=0; i<6; i++) -
{ -
cout<<a[i]<<" "; -
} -
cout<<endl; -
cout<<"数组a的最大连续子段和为:"<<MaxSum(6,a)<<endl; -
return 0; -
} -
int MaxSubSum(int *a,int left,int right) -
{ -
int sum = 0; -
if(left == right) -
{ -
sum = a[left]>0?a[left]:0; -
} -
else -
{ -
int center = (left+right)/2; -
int leftsum = MaxSubSum(a,left,center); -
int rightsum = MaxSubSum(a,center+1,right); -
int s1 = 0; -
int lefts = 0; -
for(int i=center; i>=left;i--) -
{ -
lefts += a[i]; -
if(lefts>s1) -
{ -
s1=lefts; -
} -
} -
int s2 = 0; -
int rights = 0; -
for(int i=center+1; i<=right;i++) -
{ -
rights += a[i]; -
if(rights>s2) -
{ -
s2=rights; -
} -
} -
sum = s1+s2; -
if(sum<leftsum) -
{ -
sum = leftsum; -
} -
if(sum<rightsum) -
{ -
sum = rightsum; -
} -
} -
return sum; -
} -
int MaxSum(int n,int *a) -
{ -
return MaxSubSum(a,0,n-1); -
}
算法所需的计算时间T(n)满足一下递归式:
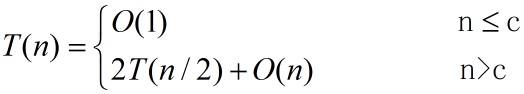
解此递归方程可知:T(n)=O(nlogn)。
(3)动态规划算法求解
算法思路如下:
记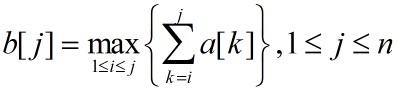 ,则所求的最大子段和为:
,则所求的最大子段和为: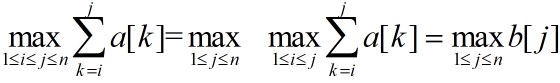
由b[j]的定义知,当b[j-1]>0时,b[j]=b[j-1]+a[j],否则b[j]=a[j]。由此可得b[j]的动态规划递推式如下:
b[j]=max{b[j-1]+a[j],a[j]},1<=j<=n。
具体代码如下:
-
//3d4-1 最大子段和问题的动态规划算法 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSum(int n,int *a); -
int main() -
{ -
int a[] = {-2,11,-4,13,-5,-2}; -
for(int i=0; i<6; i++) -
{ -
cout<<a[i]<<" "; -
} -
cout<<endl; -
cout<<"数组a的最大连续子段和为:"<<MaxSum(6,a)<<endl; -
return 0; -
} -
int MaxSum(int n,int *a) -
{ -
int sum=0,b=0; -
for(int i=1; i<=n; i++) -
{ -
if(b>0)//判断b的值为正或者是负,若是正继续加 -
{ -
b+=a[i]; -
} -
else -
{ -
b=a[i]; -
} -
if(b>sum) -
{ -
sum = b; -
} -
} -
return sum; -
}
上述算法的时间复杂度和空间复杂度均为O(n)。
2、最大子矩阵和问题
(1)问题描述:给定一个m行n列的整数矩阵A,试求A的一个子矩阵,时期各元素之和为最大。
(2)问题分析:
用二维数组a[1:m][1:n]表示给定的m行n列的整数矩阵。子数组a[i1:i2][j1:j2]表示左上角和右下角行列坐标分别为(i1,j1)和(i2,j2)的子矩阵,其各元素之和记为: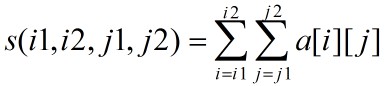
最大子矩阵问题的最优值为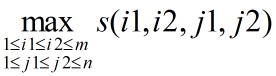 。如果用直接枚举的方法解最大子矩阵和问题,需要O(m^2n^2)时间。注意到
。如果用直接枚举的方法解最大子矩阵和问题,需要O(m^2n^2)时间。注意到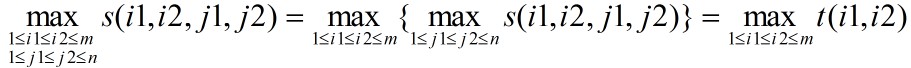 ,式中,
,式中,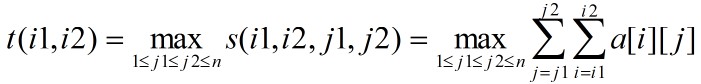 ,设
,设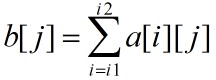 ,则
,则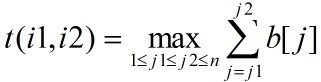
容易看出,这正是一维情形的最大子段和问题。因此,借助最大子段和问题的动态规划算法MaxSum,可设计出最大子矩阵和动态规划算法如下:
-
//3d4-5 最大子矩阵之和问题 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
const int M=4; -
const int N=3; -
int MaxSum(int n,int *a); -
int MaxSum2(int m,int n,int a[M][N]); -
int main() -
{ -
int a[][N] = {{4,-2,9},{-1,3,8},{-6,7,6},{0,9,-5}}; -
for(int i=0; i<M; i++) -
{ -
for(int j=0; j<N; j++) -
{ -
cout<<a[i][j]<<" "; -
} -
cout<<endl; -
} -
cout<<endl; -
cout<<"数组a的最大连续子段和为:"<<MaxSum2(M,N,a)<<endl; -
return 0; -
} -
int MaxSum2(int m,int n,int a[M][N]) -
{ -
int sum = 0; -
int *b = new int[n+1]; -
for(int i=0; i<m; i++)//枚举行 -
{ -
for(int k=0; k<n;k++) -
{ -
b[k]=0;//初始化为0 这个数组十分巧妙,可以解决求和问题 -
} -
for(int j=i;j<m;j++)//枚举初始行i,结束行j -
{ -
for(int k=0; k<n; k++) -
{ -
b[k] += a[j][k];//b[k]为纵向列之和 -
int max = MaxSum(n,b); -
if(max>sum) -
{ -
sum = max; -
} -
} -
} -
} -
return sum; -
} -
int MaxSum(int n,int *a) -
{ -
int sum=0,b=0; -
for(int i=1; i<=n; i++) -
{ -
if(b>0) -
{ -
b+=a[i]; -
} -
else -
{ -
b=a[i]; -
} -
if(b>sum) -
{ -
sum = b; -
} -
} -
return sum; -
}
以上代码MaxSum2方法的执行过程可用下图表示:
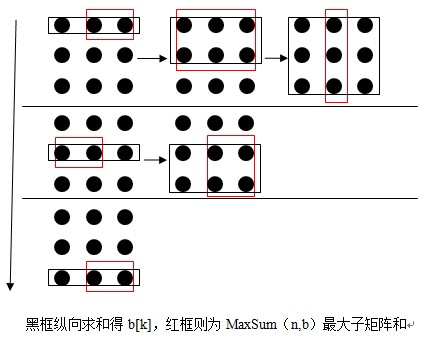
3、最大m子段和问题
(1)问题描述:给定由n个整数(可能为负数)组成的序列a1,a2,a3……an,以及一个正整数m,要求确定此序列的m个不相交子段的总和达到最大。最大子段和问题是最大m字段和问题当m=1时的特殊情形。
(2)问题分析:设b(i,j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j](1<=i<=m,i<=j<=n),则所求的最优值显然为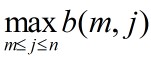 。与最大子段问题相似,计算b(i,j)的递归式为:
。与最大子段问题相似,计算b(i,j)的递归式为: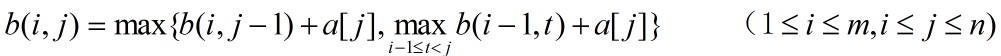
其中,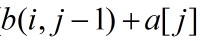 表示第i个子段含a[j-1],而
表示第i个子段含a[j-1],而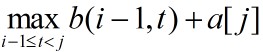 项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
具体代码如下:
-
//3d4-6 最大m子段问题 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSum(int m,int n,int *a); -
int main() -
{ -
int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始 -
for(int i=1; i<=6; i++) -
{ -
cout<<a[i]<<" "; -
} -
cout<<endl; -
cout<<"数组a的最大连续子段和为:"<<MaxSum(3,6,a)<<endl; -
} -
int MaxSum(int m,int n,int *a) -
{ -
if(n<m || m<1) -
return 0; -
int **b = new int *[m+1]; -
for(int i=0; i<=m; i++) -
{ -
b[i] = new int[n+1]; -
} -
for(int i=0; i<=m; i++) -
{ -
b[i][0] = 0; -
} -
for(int j=1;j<=n; j++) -
{ -
b[0][j] = 0; -
} -
//枚举子段数目,从1开始,迭代到m,递推出b[i][j]的值 -
for(int i=1; i<=m; i++) -
{ -
//n-m+i限制避免多余运算,当i=m时,j最大为n,可据此递推所有情形 -
for(int j=i; j<=n-m+i; j++) -
{ -
if(j>i) -
{ -
b[i][j] = b[i][j-1] + a[j];//代表a[j]同a[j-1]一起,都在最后一子段中 -
for(int k=i-1; k<j; k++) -
{ -
if(b[i][j]<b[i-1][k]+a[j]) -
b[i][j] = b[i-1][k]+a[j];//代表最后一子段仅包含a[j] -
} -
} -
else -
{ -
b[i][j] = b[i-1][j-1]+a[j];//当i=j时,每一项为一子段 -
} -
} -
} -
int sum = 0; -
for(int j=m; j<=n; j++) -
{ -
if(sum<b[m][j]) -
{ -
sum = b[m][j]; -
} -
} -
return sum; -
}
上述算法的时间复杂度为O(mn^2),空间复杂度为O(mn)。其实,上述算法中,计算b[i][j]时,只用到了数组b的第i-1行和第i行的值。因而,算法中只要存储数组b的当前行,不必存储整个数组。另一方面,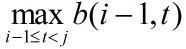 的值可以在计算i-1行时预先计算并保存起来。计算第i行的值时不必重新计算,节省了计算时间和空间。因此,算法可继续改进如下:
的值可以在计算i-1行时预先计算并保存起来。计算第i行的值时不必重新计算,节省了计算时间和空间。因此,算法可继续改进如下:
-
//3d4-7 最大m子段问题 -
#include "stdafx.h" -
#include <iostream> -
using namespace std; -
int MaxSum(int m,int n,int *a); -
int main() -
{ -
int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始 -
for(int i=1; i<=6; i++) -
{ -
cout<<a[i]<<" "; -
} -
cout<<endl; -
cout<<"数组a的最大连续子段和为:"<<MaxSum(3,6,a)<<endl; -
} -
int MaxSum(int m,int n,int *a) -
{ -
if(n<m || m<1) -
return 0; -
int *b = new int[n+1]; -
int *c = new int[n+1]; -
b[0] = 0;//b数组记录第i行的最大i子段和 -
c[1] = 0;//c数组记录第i-1行的最大i-1子段和 -
for(int i=1; i<=m; i++) -
{ -
b[i] = b[i-1] + a[i]; -
c[i-1] = b[i]; -
int max = b[i]; -
//n-m+i限制避免多余运算,当i=m时,j最大为n,可据此递推所有情形 -
for(int j=i+1; j<=i+n-m;j++) -
{ -
b[j] = b[j-1]>c[j-1]?b[j-1]+a[j]:c[j-1]+a[j]; -
c[j-1] = max;//预先保存第j-1行的最大j-1子段和 -
if(max<b[j]) -
{ -
max = b[j]; -
} -
} -
c[i+n-m] = max; -
} -
int sum = 0; -
for(int j=m; j<=n; j++) -
{ -
if(sum<b[j]) -
{ -
sum = b[j]; -
} -
} -
return sum; -
}
上述算法时间复杂度为O(m(n-m)),空间复杂度为O(n)。当m或n-m为常数时,时间复杂度和空间复杂度均为O(n)。
--------------------- 本文来自 风仲达 的CSDN 博客 ,全文地址请点击:https://blog.csdn.net/liufeng_king/article/details/8632430?utm_source=copy


