用于图像数据集预处理的K-means聚类算法_kmeans图像分类

一、数据集和模型文件准备

1.1 数据集下载

使用kaggle猫狗大战的test中的前100张图像作为数据集1：dogs-vs-cats

使用100张红外船舶图像作为数据集2：

1.2 模型文件下载(可忽略)

通过使用更大、更复杂的模型，可以获得更高的准确率，预训练模型是一个很好的选择，我们可以直接使用预训练模型来完成分类任务，因为预训练模型通常已经在大型的数据集上进行过训练，通常用于完成大型的图像分类任务。

tf.keras.applications中有一些预定义好的经典卷积神经网络结构（Application应用）:

我们可以直接调用这些经典的卷积神经网络结构（甚至载入预训练的参数），而无需手动来构建网络结构。

例如，本文将要用到的模型是由谷歌开发的 MobileNetV2 网络结构，该模型已经在 ImageNet 数据集上进行过预训练，共含有 1.4M 张图像，而且学习了常见的 1000 种物体的基本特征，因此，该模型具有强大的特征提取能力。

model = tf.keras.applications.MobileNetV2()
1

当执行以上代码时，TensorFlow会自动从网络上下载 MobileNetV2 网络结构，运行代码后需要等待一会会儿~~。MobileNetV2模型的速度很快，而且耗费资源也不是很多。

二、K-means聚类实现数据集的聚类

2.1 K-means的原理和算法

详细原理：【机器学习】K-means（非常详细）
定义
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，聚类技术经常被称为无监督学习。

k均值聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

算法
先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个：

• 没有（或最小数目）对象被重新分配给不同的聚类。
• 没有（或最小数目）聚类中心再发生变化。
• 误差平方和局部最小。

2.2 K-means中K值的最合适取值

学习总结：K-Means算法之K值的选择

2.2.1 肘部法

2.2.1.1 手肘法的核心思想
随着聚类数$k$的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于最佳聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大；而当k到达最佳聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减；然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的最佳聚类数。这也是该方法被称为手肘法的原因。

由下图，y轴为SSE（Sum of the Squared Errors-误差平方和），x轴为k的取值。随着x的增加，SSE会随之降低，当下降幅度明显趋向于缓慢的时候，取该值为K的值。

1. 对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和；
2. 平方和是会逐渐变小的，直到k时平方和为0，因为每个点都是它所在的簇中心本身。
3. 在这个平方和变化过程中，会出现一个拐点也即“肘”点，下降率突然变缓时即认为是佳的k值。

2.2.1.2 SSE
手肘法的评价K值好坏的标准是SSE。
$$SSE=\sum _{p\in C_i}|p-m_i{|}^2$$
其中$C_i$代表第$i$个簇，$p$是簇$C_i$里的样本点，$m_i$是簇的质心。

2.2.1.3 应用

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
# 生成数据
X, y = make_blobs(n_samples=300, centers=5, n_features=5, random_state=0)

start_k=2
end_k=20
SSE = []
model = [] #保存每次的模型
kt=[]
for i in range(start_k, end_k):
    kMeans = KMeans(n_clusters=i)
    kMeans.fit(X)
    SSE.append(kMeans.inertia_)  # 保存每一个k值的SSE值
    print('{} Means SSE loss = {}'.format(i, kMeans.inertia_))
    model.append(kMeans)
    kt.append(i)
plt.plot(kt, SSE)
plt.ylabel('Means SSE loss')
plt.ylabel('SSE ')
plt.show()


# 求二阶导数，通过sse方法计算最佳k值
kl=[]
SSE_d1 = [] #sse的一阶导数
SSE_d2 = [] #sse的二阶导数
SSE_length = len(SSE)
for i in range(1, SSE_length):
    SSE_d1.append((SSE[i - 1] - SSE[i]) / 2)
for i in range(1, len(SSE_d1) - 1):
    SSE_d2.append((SSE_d1[i - 1] - SSE_d1[i]) / 2)
    kl.append(i)
best_model = model[SSE_d2.index(max(SSE_d2)) + 2]
print(best_model)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

2.2.2 轮廓法

2.2.2.1 概述

通过聚类后的结果label来计算的一种评价指标。内部有效性指标呢设计的时候从三个方面来看聚类的有效性：

• 度量各个聚类的分离程度，理论上，类分离程度越大，结果越好。
• 度量每个类内的内在紧致性，紧致性越大，聚类效果越好。
• 度量各个类表示的复杂度，在可行的类表示中选择简单的。

在聚类问题中，Silhouette分析用来研究聚类结果的类间距离。Silhouette数值度量在相同类中的点，与不同类中的点相比的紧密程度。Silhouette图可视化这一测度，这样就提供了一种评价类个数的方法。使用Silhouette分析选择一个类个数参数n_clusters的最优值。

Silhouette 遵循类紧致性。Silhouette值用来描述一个目标对于目标所在簇与其他簇之间的相似性。其范围是从-1~+1，这个值越大表明目标与自己所在簇之间的匹配关系度越高，与其他簇的匹配关系度越低。如果这个值越高，那么聚类结果越好，如果是很小或是负值，那么可能是分簇太多或是太少造成的。Silhouette是通过一些距离矩阵来计算的。

2.2.2.2 Silhouette的定义

• 簇内不相似度
  假设数据集我们已经通过聚类算法分成了很多类。对于目标$i$有$i\in C_i$得到：
  $$a(i)=\frac{1}{|C_i-1|}\sum _{j\in C_i，i\ne j}d(i,j)$$
  表示i与同簇之间其他目标的平均距离。
  这里的$d(i,j)$是目标$i$和$j$在簇$C_i$ 中的距离。那么$a(i)$可以说成是$i$被分配到这个簇的好坏程度。

• 簇间不相似度
  对于目标$i$有$i\in C_i$,$C_k$表示第$k$个簇:
  $$b(i)=\underset{k\ne i}{\min }\frac{1}{|C_k|}\sum _{j\in C_k}d(i,j)$$
  表示$i$到除$C_i$ 簇外其他簇$C_k$中的点之间的平均距离作为簇之间的平均不相似度。我们用$i$到其它簇的最小平均距离表示$b(i)$。

• Silhouette值
  根据样本i的簇内不相似度$a(i)$和簇间不相似度$b(i)$ ，定义样本$i$的轮廓系数:
  s ( i ) = { b ( i ) − a ( i ) m a x ( a ( i ) , b ( i ) ) ， if  ∣ C i ∣ > 1 0 if  ∣ C i ∣ = 1 s(i)=

  $$\begin{cases} \cfrac{b(i)-a(i)}{max(a(i),b(i))}， &\text{if } |C_i|>1 \\ 0 &\text{if } |C_i|=1 \end{cases}$$ s(i)=⎩⎨⎧​max(a(i),b(i))b(i)−a(i)​，0​if ∣Ci​∣>1if ∣Ci​∣=1​
  同时也可以写成：
  $$s(i)=\{\begin{array}{ll}1-\frac{a(i)}{b(i)}，& \text{if }a(i)<b(i)\\ 0，& \text{if }a(i)=b(i)\\ \frac{b(i)}{a(i)}-1，& \text{if }a(i)>b(i)\end{array}$$

• 轮廓系数范围在[-1,1]之间。该值越大，越合理。
• $s(i)$接近1，则说明样本i聚类合理。对于簇中值$i$来说$a(i)$越小，那么$i$被分配到这个簇是很合理的;
• si接近-1，则说明样本i更应该分类到另外的簇；
• 若si 近似为0，则说明样本i在两个簇的边界上。

2.2.2.3 Silhouette coefficient
所有样本的$s(i)$的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。silhouette coefficient表示在整个数据集上s(i)的均值的最大值。可得到:
$$SC=\underset{k}{\max }\bar{s}(k)$$
在sklearn包中已经有用python实现的轮廓系数值的计算。

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt

# 生成数据
X, y = make_blobs(n_samples=300, centers=5, n_features=5, random_state=0)

# 寻找最合适的K值
sil = []
kl = []
beginK = 3
endK = 8
for k in range(beginK, endK):
    kMeans = KMeans(n_clusters=k)
    kMeans.fit(X)  # 聚类
    SC = silhouette_score(X, kMeans.labels_, metric='euclidean')
    sil.append(SC)
    kl.append(k)
plt.plot(kl, sil)
plt.ylabel('Silhoutte Score')
plt.ylabel('K')
plt.show()

# k-means聚类
bestK = kl[sil.index(max(sil))]
km = KMeans(n_clusters=bestK)
km.fit(X)
y_predict = km.predict(X)
# 评估聚类效果
print(silhouette_score(X, y_predict))
# 绘制聚类结果图
color = ["red", "green", "blue", "gray", "yellow"]
colors = [color[i] for i in y_predict]
plt.figure()
plt.scatter(X[:, 1], X[:, 2], color=colors)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

从图可见，当k值为5时最合适。

关于函数的讲解和具体应用实例官方文档：sklearn.metrics.silhouette_score

2.3 K-means在图像聚类上的应用

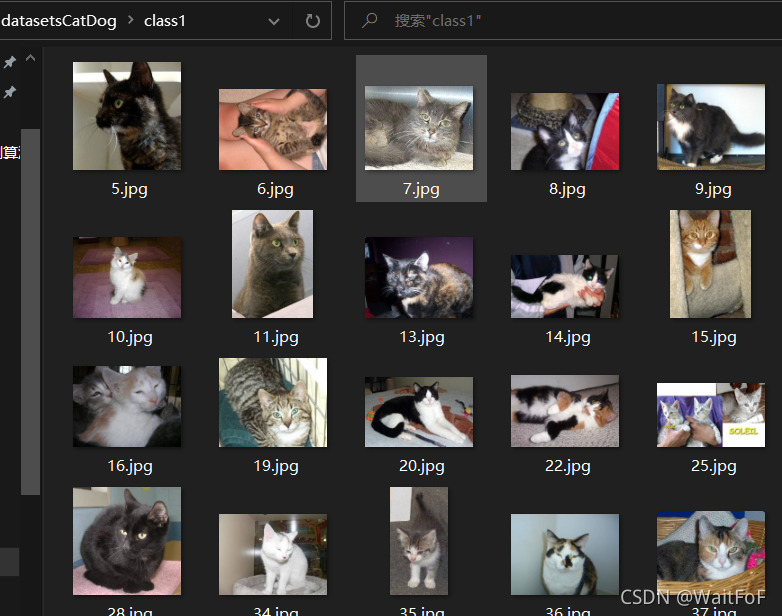
2.3.1 对猫狗进行聚类

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import cv2
import os, glob, shutil


# 1.获取所有图像
input_dir = 'datasetsCatDog'
glob_dir = input_dir + '/*.jpg'
#opencv读取图像，并将图像大小 resize 为（224，224），以匹配模型输入层的大小以进行特征提取。
images = [cv2.resize(cv2.imread(file), (224, 224)) for file in glob.glob(glob_dir)]
paths = [file for file in glob.glob(glob_dir)]
# 图像数组转换为 float32 类型并reshape，然后做归一化。
images = np.array(np.float32(images).reshape(len(images), -1) / 255)
#绘制数据分布图
plt.scatter(images[:, 0], images[:, 1], c = "red", marker='o', label='origin')
plt.xlabel('length')
plt.ylabel('width')
plt.legend(loc=2)
plt.show()



# 2.加载预先训练的模型MobileNetV2来实现图像分类
model = tf.keras.applications.MobileNetV2(include_top=False, weights='imagenet', input_shape=(224, 224, 3)) #'imagenet' (pre-training on ImageNet),
predictions = model.predict(images.reshape(-1, 224, 224, 3))
pred_images = predictions.reshape(images.shape[0], -1)

# 3. 使用轮廓法寻找K值
sil = []
kl = []
kmax = 4 #设置最大的K值
for k in range(2, kmax + 1):
    kMeans = KMeans(n_clusters=k).fit(pred_images)#构造聚类器 聚类
    labels = kMeans.labels_ #获取聚类标签
    sil.append(silhouette_score(pred_images, labels, metric='euclidean')) # 计算所有样本的平均剪影系数。
    kl.append(k)

bestK = kl[sil.index(max(sil))]
print(bestK)
plt.plot(kl, sil)
plt.ylabel('Silhoutte Score')
plt.ylabel('K')
plt.show()

# 4. 使用最合适的K值进行聚类
k = bestK
kMeansModel = KMeans(n_clusters=k,  random_state=888)#构造聚类器
kMeansModel.fit(pred_images)#聚类
label_pred = kMeansModel.labels_  # 获取聚类标签
kPredictions = kMeansModel.predict(pred_images)
print(kPredictions)
#绘制 k-means结果
for j in range(0,k):
    imagesRes = images[label_pred == j]
    plt.scatter(imagesRes[:, 0], imagesRes[:, 1],  label=('label'+str(j)))
    plt.xlabel(' length')
    plt.ylabel(' width')
    plt.legend(loc=2)
plt.show()



# 5. 保存图像到不同类别的文件夹
for i in range(1,k+1):
    name="datasetsCatDog/class" + str(i)
    if os.path.isdir(name):
        #os.rmdir(name)# 删除目录 如果该目录非空则不能删除
        shutil.rmtree(name)# 删除目录 如果该目录非空也能删除
    os.mkdir("datasetsCatDog/class" + str(i))
for i in range(len(paths)):
    for j in range(0,k):
        if kPredictions[i] == j:
            shutil.copy(paths[i], "datasetsCatDog/class"+str(j+1))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

三、问题

AttributeError: ‘str’ object has no attribute ‘decode’
卸载原来的h5py模块，安装2.10版本：
pip install h5py==2.10 -i https://pypi.tuna.tsinghua.edu.cn/simple/

参考：Tensorflow2.0和keras版本兼容问题