devbox
小蓝xlanll
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

干货 | 20个Python教程，掌握时间序列的特征分析（附代码）

作者：小蓝xlanll | 2024-02-26 07:45:13

赞

踩

python 特征分析 常见思路 代码

点击上方“Python数据之道”，选择“星标公众号”

收藏文章的同时，不要忘记「在看」

640?wx_fmt=jpeg

作者 | Selva Prabhakaran 

译者 | Tianyu

编辑 | Jane

来源 | AI科技大本营（ID: rgznai100）

【导语】时间序列是指以固定时间为间隔的序列值。本篇教程将教大家用 Python 对时间序列进行特征分析。

 

1、什么是时间序列？

时间序列是指以固定时间为间隔的、由所观察的值组成的序列。根据观测值的不同频率，可将时间序列分成小时、天、星期、月份、季度和年等时间形式的序列。有时候，你也可以将秒钟和分钟作为时间序列的间隔，如每分钟的点击次数和访客数等等。

 

为什么我们要对时间序列进行分析呢？

 

因为当你想对一个序列进行预测时，首先要完成分析这个步骤。除此之外，时间序列的预测也具有极大商业价值，如企业的供求量、网站的访客量以及股票价格等，都是极其重要的时间序列数据。

 

那么，时间序列分析都包括哪些内容呢？

 

要做好时间序列分析，必须要理解序列的内在属性，这样才能做出更有意义且精准的预测。

2、如何在 Python 中引入时间序列？

关于时间序列的数据大都存储在 csv 文件或其他形式的表格文件里，且都包含两个列：日期和观测值。

 

首先我们来看 panda 包里面的 read_csv() 函数，它可以将时间序列数据集（关于澳大利亚药物销售的 csv 文件）读取为 pandas 数据框。增加一个 parse_dates=['date'] 字段，可以把包含日期的数据列解析为日期字段。

  1. from dateutil.parser import parse 	
  2. import matplotlib as mpl	
  3. import matplotlib.pyplot as plt	
  4. import seaborn as sns	
  5. import numpy as np	
  6. import pandas as pd	
  7. plt.rcParams.update({'figure.figsize': (10, 7), 'figure.dpi': 120})	
  8.  
  9. 	
  10. # Import as Dataframe	
  11. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])	
  12. df.head()

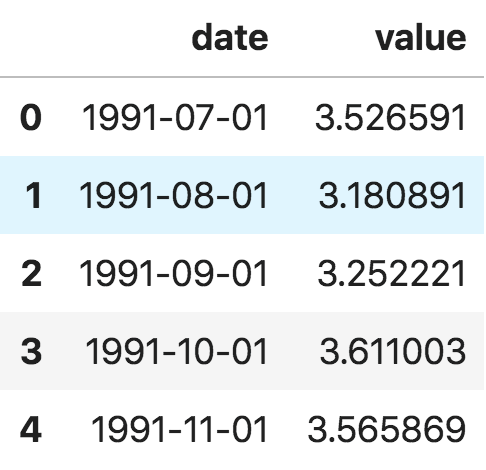
640?wx_fmt=png

时间序列数据框

 

此外，你也可以将文件读取为 pandas 序列，把日期作为索引列，只需在 pd.read_csv() 中指定 index_col 参数。

  1. ser = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')	
  2. ser.head()

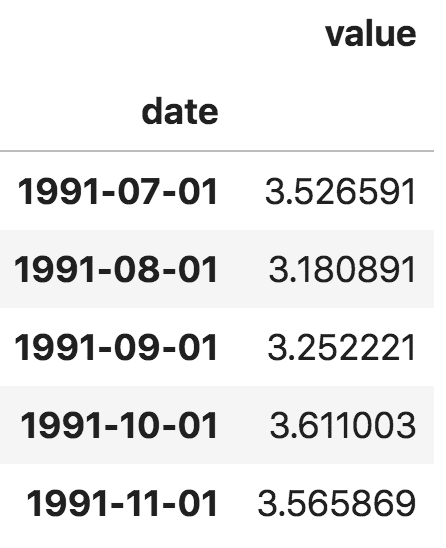
640?wx_fmt=png

pandas 序列

 

注意，在 pandas 序列中，'value' 列的位置高于 'date' 列，这表明它是一个 pandas 序列而非数据框。

 

3、什么是面板数据？

面板数据同样是基于时间的数据集。

 

不同之处是，除了时间序列，面板数据还包括一个或多个相关变量，这些变量也是在同个时间段内测得的。

 

面板数据中的列包括有助于预测 y 值的解释变量，这些特征列可用于之后的预测。以下是关于面板数据的例子：

  1. # dataset source: https://github.com/rouseguy	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/MarketArrivals.csv')	
  3. df = df.loc[df.market=='MUMBAI', :]	
  4. df.head()

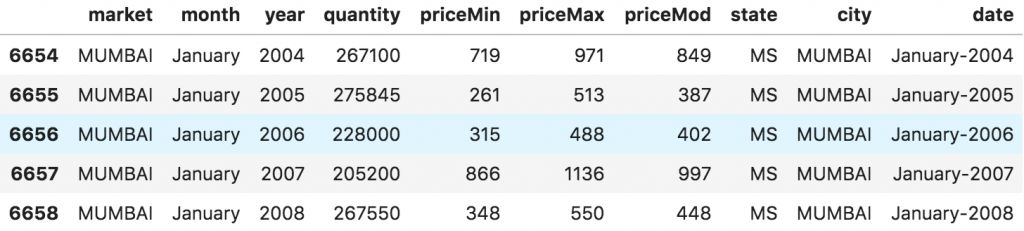
640?wx_fmt=png

面板数据

4、时间序列可视化

接下来，我们用 matplotlib 对序列进行可视化。

 
 
 
 
 
 
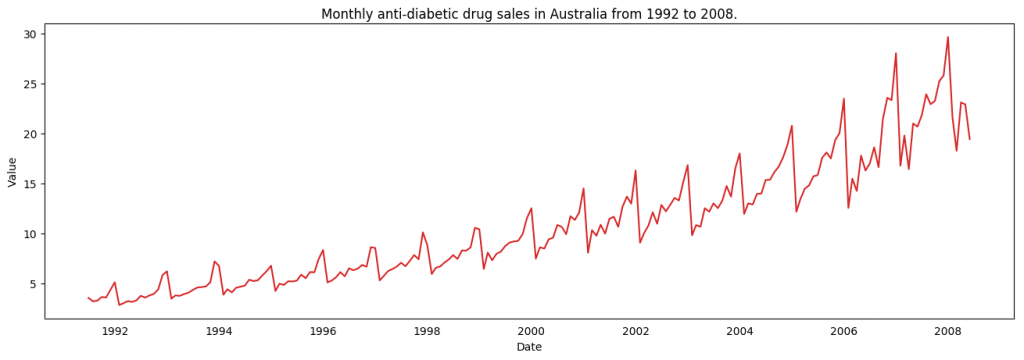
640?wx_fmt=png
 
 
时间序列可视化
 
 
 
 
 
由于所有的值都为正数，无论使用 y 轴的哪一侧都可以看到增长的趋势。
 
 
  1. # Import data	
  2. df = pd.read_csv('datasets/AirPassengers.csv', parse_dates=['date'])	
  3. x = df['date'].values	
  4. y1 = df['value'].values	
  5.  
  6. 	
  7. # Plot	
  8. fig, ax = plt.subplots(1, 1, figsize=(16,5), dpi= 120)	
  9. plt.fill_between(x, y1=y1, y2=-y1, alpha=0.5, linewidth=2, color='seagreen')	
  10. plt.ylim(-800, 800)	
  11. plt.title('Air Passengers (Two Side View)', fontsize=16)	
  12. plt.hlines(y=0, xmin=np.min(df.date), xmax=np.max(df.date), linewidth=.5)	
  13. plt.show()
 
 
 
 
 
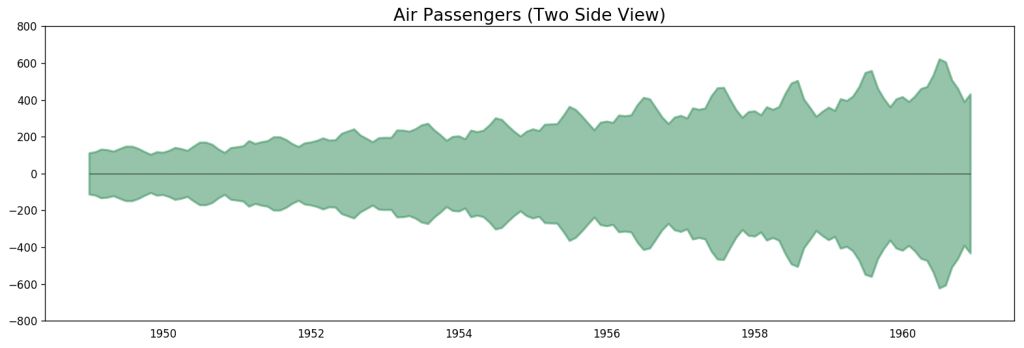
640?wx_fmt=png
 
 
飞机乘客数据 - 双边序列
 
 
 
 
 
由于这是一个月份的时间序列，每年的走势都遵循着特定重复的模式，你可以在同一个图中画出单独每年的折线。这样有助于对这几年的趋势走向进行平行对比。
 
 
 
 
 
季节性时间序列的可视化：
 
 
 
 
 
 
  1. # Import Data	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')	
  3. df.reset_index(inplace=True)	
  4.  
  5. 	
  6. # Prepare data	
  7. df['year'] = [d.year for d in df.date]	
  8. df['month'] = [d.strftime('%b') for d in df.date]	
  9. years = df['year'].unique()	
  10.  
  11. 	
  12. # Prep Colors	
  13. np.random.seed(100)	
  14. mycolors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)	
  15.  
  16. 	
  17. # Draw Plot	
  18. plt.figure(figsize=(16,12), dpi= 80)	
  19. for i, y in enumerate(years):	
  20.     if i > 0:	
  21.         plt.plot('month', 'value', data=df.loc[df.year==y, :], color=mycolors[i], label=y)	
  22.         plt.text(df.loc[df.year==y, :].shape[0]-.9, df.loc[df.year==y, 'value'][-1:].values[0], y, fontsize=12, color=mycolors[i])	
  23.  
  24. 	
  25. # Decoration	
  26. plt.gca().set(xlim=(-0.3, 11), ylim=(2, 30), ylabel='$Drug Sales$', xlabel='$Month$')	
  27. plt.yticks(fontsize=12, alpha=.7)	
  28. plt.title("Seasonal Plot of Drug Sales Time Series", fontsize=20)	
  29. plt.sho
 
 
 
 
 
 
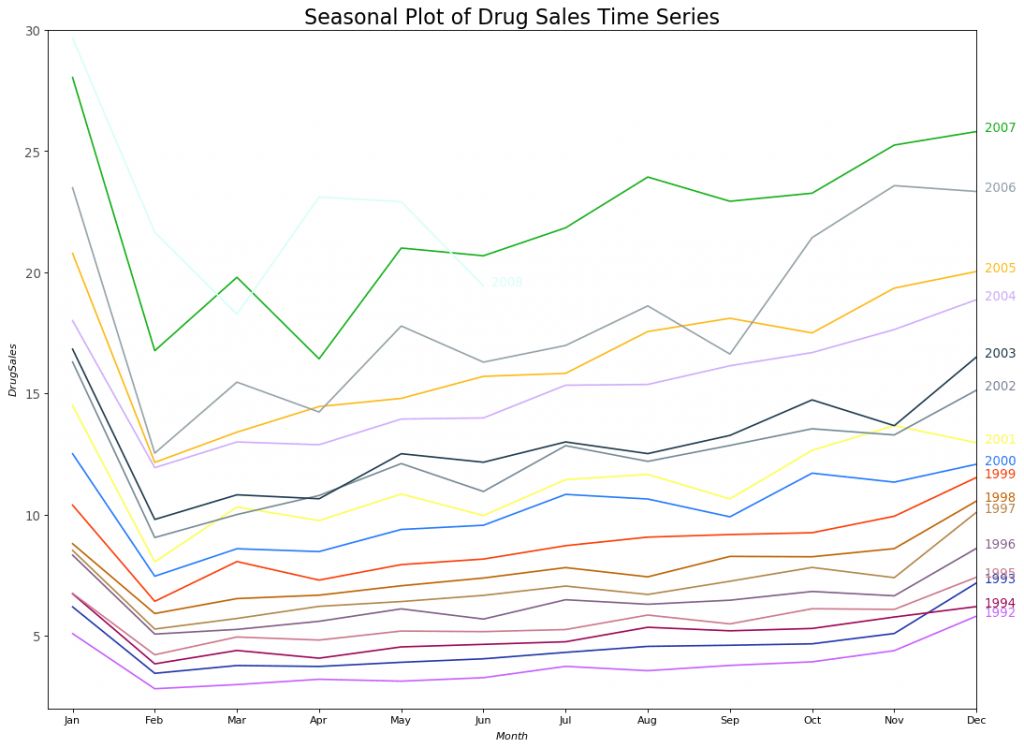
640?wx_fmt=png
 
 
药品销售的季节性时间序列图
 
 
 
 
 
每年的二月份，药品销售会有一次大幅度下跌，三月份会回涨，四月份再次下跌，以此规律循环。很明显，该模式以年为单位，每年循环往复。
 
 
 
 
 
不过，随着年份的变化，药品销售总体呈上升趋势。你可以选择使用箱型图将这一趋势进行可视化，可以方便看出每一年的变化。同样地，你也可以按月份绘制箱型图，来观察每个月的变化。
 
 
 
 
 
按月份（季节）和年份绘制箱型图：你可以将数据处理成以季节为时间间隔，然后观察特定年份内值的分布，也可以将全部时间的数据进行对比。
 
 
  1. # Import Data	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')	
  3. df.reset_index(inplace=True)	
  4.  
  5. 	
  6. # Prepare data	
  7. df['year'] = [d.year for d in df.date]	
  8. df['month'] = [d.strftime('%b') for d in df.date]	
  9. years = df['year'].unique()	
  10.  
  11. 	
  12. # Draw Plot	
  13. fig, axes = plt.subplots(1, 2, figsize=(20,7), dpi= 80)	
  14. sns.boxplot(x='year', y='value', data=df, ax=axes[0])	
  15. sns.boxplot(x='month', y='value', data=df.loc[~df.year.isin([1991, 2008]), :])	
  16.  
  17. 	
  18. # Set Title	
  19. axes[0].set_title('Year-wise Box Plot\n(The Trend)', fontsize=18);	
  20. axes[1].set_title('Month-wise Box Plot\n(The Seasonality)', fontsize=18)	
  21. plt.show
 
 
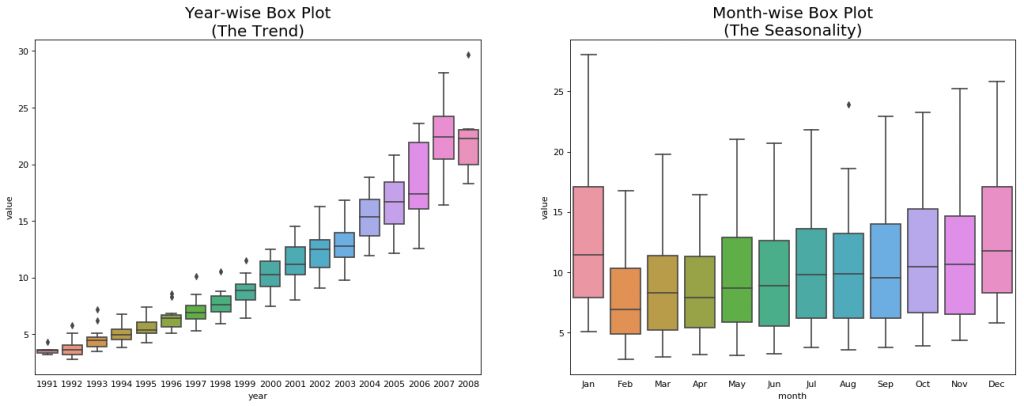
640?wx_fmt=png
 
 
年份序列和月份序列的箱型图
 
 
 
 
 
上面的箱型图可以使年份和月份的序列更易于观察。同样，在月份的箱线图中，十二月和一月的药品销售额明显更高，这是因为处于假期折扣季。
 
 
 
 
 
到目前为止，我们了解了通过相似性来观察时间序列的模式，接下来，如何发现这些常见模式中的差异呢？
 
 
 
 
 
5、时间序列的模式
 
 
 
 
任何一个时间序列都可以被分解成以下几个部分：基准 + 趋势成分 + 季节成分 + 残差成分。
 
 
 
 
 
趋势是指时间序列中上升或下降的倾斜程度。但季节成分是由于受季节因素影响而产生的周期性模式循环，也可能受每年内不同月份、每月内不同日期、工作日或周末，甚至每天内不同时间的影响。
 
 
 
 
 
然而，不一定所有的时间序列都具备趋势或季节性。一个时间序列也可能不存在趋势，但具有季节性。反之亦然。
 
 
 
 
 
因此，一个时间序列可以被想象成趋势、季节性和残差项的组合。
 
 
 
 
 
 
 
 
 
 
 
 
 
 
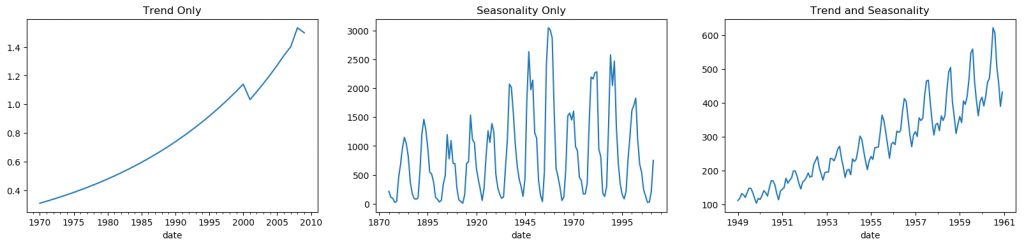
640?wx_fmt=png
 
 
时间序列的模式
 
 
 
 
 
另一个需要考虑的方面是周期性模式。当序列中的上升和下降，不是按日历中的特定时间间隔发生时，就会出现这种情况。注意不要把“周期”作用和“季节”作用混淆。
 
 
 
 
 
那么，如何区分“周期”和“季节”呢？
 
 
 
 
 
如果序列中的模式不是以日历中特定间隔循环出现的，那么就是周期。因为与季节性不同，周期作用通常受到商业或社会经济等因素的影响。
 
 
 
 
 
6、加法与乘法时间序列
 
 
 
 
根据趋势和季节的固有属性，一个时间序列可以被建模为加法模型或乘法模型，也就是说，序列中的值可以用各个成分的加和或乘积来表示：
 
 
 
 
 
加法时间序列：
 
 
值 = 基准 + 趋势 + 季节 + 残差
 
 
 
 
 
乘法时间序列：
 
 
值 = 基准 x 趋势 x 季节 x 残差
 
 
 
 
 
7、如何将时间序列的成分分解出来？
 
 
 
 
通过将一个时间序列视为基准、趋势、季节指数及残差的加法或乘法组合，你可以对时间序列进行经典分解。
 
 
 
 
 
 
 
 
  1. statsmodels 的 seasonal_decompose 函数可以使这一过程非常容易。	
  2.  	
  3. from statsmodels.tsa.seasonal import seasonal_decompose	
  4. from dateutil.parser import parse	
  5.  
  6. 	
  7. # Import Data	
  8. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')	
  9.  
  10. 	
  11. # Multiplicative Decomposition	
  12. result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')	
  13.  
  14. 	
  15. # Additive Decomposition	
  16. result_add = seasonal_decompose(df['value'], model='additive', extrapolate_trend='freq')	
  17.  
  18. 	
  19. # Plot	
  20. plt.rcParams.update({'figure.figsize': (10,10)})	
  21. result_mul.plot().suptitle('Multiplicative Decompose', fontsize=22)	
  22. result_add.plot().suptitle('Additive Decompose', fontsize=22)	
  23. plt.sho
 
 
 
 
 
 
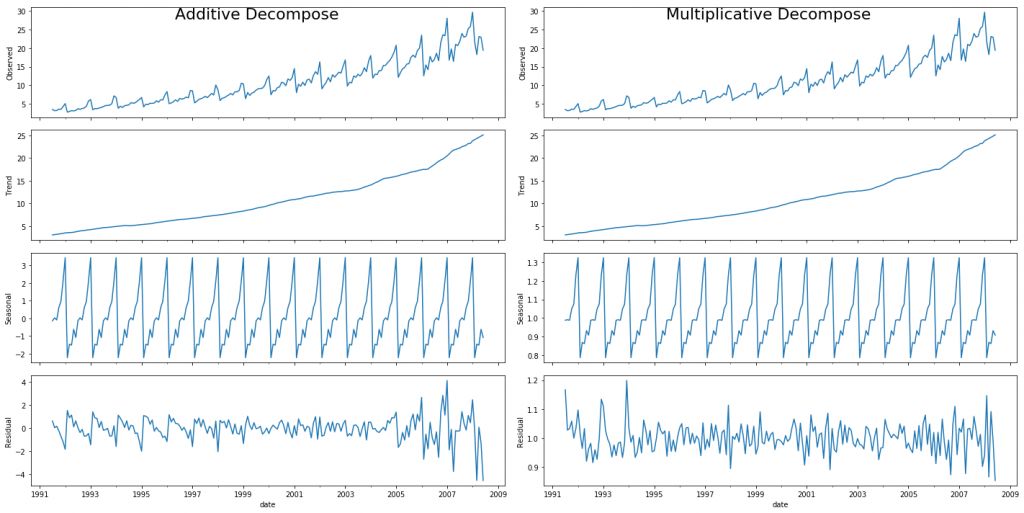
640?wx_fmt=png
 
 
加法和乘法分解
 
 
 
 
 
设置 extrapolate_trend='freq' 有助于处理序列首部趋势和残差中的空值。
 
 
 
 
 
如果你仔细观察加法分解中的残差项，会发现其中仍保留了一些模式。然而，乘法分解中的残差项看起来更具有随机性。因此，对于这一特定序列来说，采用乘法分解更合适。
 
 
 
 
 
趋势、季节和残差成分的数值输出均存储在 result_mul 里，下面我们对其进行提取，并放入数据框中：
 
 
  1. # Extract the Components ----	
  2. # Actual Values = Product of (Seasonal * Trend * Resid)	
  3. df_reconstructed = pd.concat([result_mul.seasonal, result_mul.trend, result_mul.resid, result_mul.observed], axis=1)	
  4. df_reconstructed.columns = ['seas', 'trend', 'resid', 'actual_values']	
  5. df_reconstructed.head()
 
 
仔细观察，会发现 seas、trend 和 resid 三列的乘积正好等于 actual_values。
 
 
 
 
8、平稳和非平稳时间序列
 
 
 
 
平稳是时间序列的属性之一。平稳序列中的值不是时间的函数。
 
 
 
 
 
也就是说，平稳序列的平均值、方差和自相关性等统计特征始终为常数。序列的自相关性是指该序列与之前的值间的相关性。
 
 
 
 
 
平稳的时间序列也不包括季节因素的影响。那么如何分辨一个序列是否平稳呢？让我们来看几个例子：
 
 
 
 
 
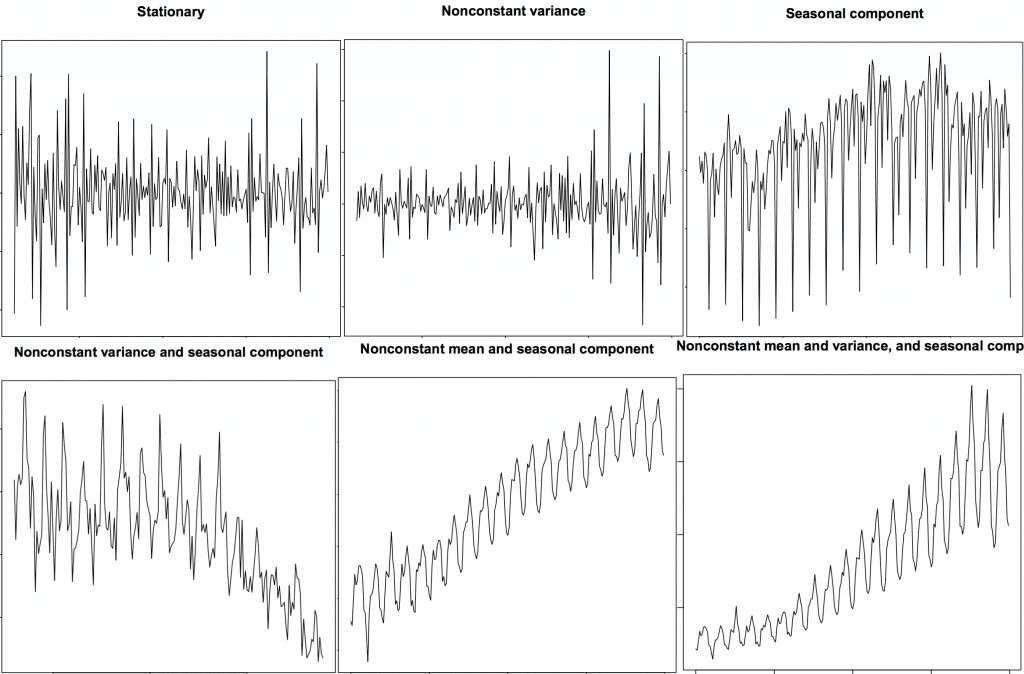
640?wx_fmt=png
 
 
平稳和非平稳时间序列
 
 
 
 
 
上图来自 R 语言的 TSTutorial 教程。
 
 
 
 
 
为什么说序列平稳很重要呢？
 
 
 
 
 
我会对此稍微做一些解释，但要清楚一点，通过采用合适的变换，我们近乎可以将任何时间序列变得平稳。大多数统计预测方法最初都是为平稳时间序列而设计的。预测过程的第一步是通过一些变换，来将非平稳序列变成平稳序列。
 
 
 
 
9、如何将时间序列变平稳？
 
 
 
 
你可以通过以下几种方式得到平稳序列：
 
 
 
 
  • 求序列的差分
  • 求序列的 log 值
  • 求序列的 n 次方根
  • 把上面三种方法相结合
 
 
 
 
将时间序列平稳化最普遍且便捷的方法是对序列进行差分运算，至少执行一次，直到序列趋于平稳。
 
 
 
 
 
那么什么是差分呢？
 
 
 
 
 
如果 Y_t 为时间 't' 对应的值，那么第一个差分值为 Y = Yt – Yt-1。简单来说，对序列进行差分运算就是用下一个值减去当前值。如果第一次差分不能使序列平稳，你可以尝试做第二次差分，直到符合要求。
 
 
 
 
 
举个例子，有这样一个序列：[1, 5, 2, 12, 20]
 
 
 
 
 
第一次差分运算的结果为：[5-1, 2-5, 12-2, 20-12] = [4, -3, 10, 8]
 
 
 
 
 
第二次差分运算的结果为：[-3-4, -10-3, 8-10] = [-7, -13, -2]
 
 
 
 
10、为什么要在预测前将非平稳序列变平稳？
 
 
 
 
对平稳序列进行预测要相对容易一些，预测结果也更可信。其中一个重要原因是，自回归预测模型本质上是线性回归模型，将序列自身的滞后作为预测因子。
 
 
 
 
 
如果预测因子之间互不相关，线性回归的效果最优。那么将序列平稳化就可以解决这一问题，因为它可以去除任何持久的自相关性，所以可以使预测模型中的预测因子近乎独立。
 
 
 
 
 
现在我们知道了使序列平稳化的重要性，那么应该如何检查一个序列是否平稳呢？
 
 
 
 
11、如何测试平稳性？
 
 
 
 
我们可以像之前那样，通过绘制序列图来观察一个序列是否平稳。
 
 
 
 
 
另一种方法是将序列分解成两个或多个连续的部分，并求其统计值，如平均值、方差和自相关系数。如果这些统计值间的差异很大，那么该序列大概率不是平稳序列。
 
 
 
 
 
尽管如此，你仍需要一种方法来定量地判断某个序列是否平稳。一个名为“单位根检验”的统计检验方法可以解决这一问题。
 
 
 
 
 
单位根检验有如下几种方法：
 
 
 
 
  • ADF Test (Augmented Dickey Fuller test)
  • KPSS Test (Kwiatkowski-Phillips-Schmidt-Shin) — 趋势平稳
  • PP Test (Philips Perron test)
 
 
 
 
最常用的方法是 ADF test，零假设为：用时间序列对单位根进行处理，结果是不平稳。如果 P 值小于显著性水平 0.05，则拒绝零假设，即不成立。
 
 
 
 
 
另一方面，KPSS test 可用来检测趋势平稳性。零假设与 P 值含义都与 ADH test 相反。以下代码基于 Python 的 statsmodels 包执行了两种检测方法：
 
 
  1. from statsmodels.tsa.stattools import adfuller, kpss	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])	
  3.  
  4. 	
  5. # ADF Test	
  6. result = adfuller(df.value.values, autolag='AIC')	
  7. print(f'ADF Statistic: {result[0]}')	
  8. print(f'p-value: {result[1]}')	
  9. for key, value in result[4].items():	
  10.     print('Critial Values:')	
  11.     print(f'   {key}, {value}')	
  12.  
  13. 	
  14. # KPSS Test	
  15. result = kpss(df.value.values, regression='c')	
  16. print('\nKPSS Statistic: %f' % result[0])	
  17. print('p-value: %f' % result[1])	
  18. for key, value in result[3].items():	
  19.     print('Critial Values:')	
  20.     print(f'   {key}, {value}'
 
 
 
 
 
 
 
 
 
 
 
 
12、白噪声与平稳序列的差别是什么？
 
 
 
 
和平稳序列一样，白噪声也是关于时间的函数，它的均值和方差始终不变。但区别在于，白噪声是完全随机的，且均值为零。
 
 
 
 
 
白噪声没有任何模式。如果你把调频广播的声波讯号想象成时间序列，调频道时的空白声音就是白噪声。
 
 
 
 
 
从数学上来讲，一个完全随机且均值为零的序列就是白噪声。
 
 
 
 
 
 
 
 
 
 
 
 
 
 
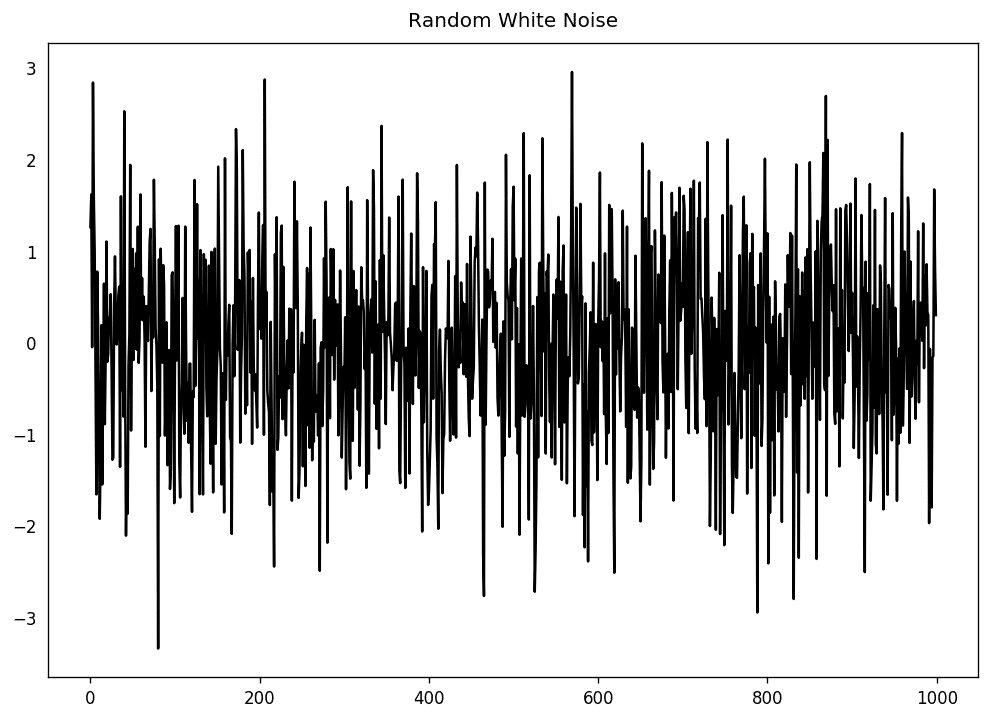
640?wx_fmt=png
 
 
随机白噪声
 
 
 
 
 
13、如何对时间序列去趋势？
 
 
 
 
对时间序列去趋势，是指去除序列中的趋势成分。但要如何提取趋势成分呢？有以下几种方法：
 
 
 
 
  • 减去与时间序列拟合程度最好的曲线。这条最优曲线可由线性回归模型获得，时间步长作为预测因子。如需处理更复杂的趋势，你可以尝试在模型中使用二次项 (x^2)。
  • 减去由时间序列分解得到的趋势成分。
  • 减去均值。
  • 使用过滤器，如 Baxter-King (statsmodels.tsa.filters.bkfilter) 或 Hodrick-Prescott (statsmodels.tsa.filters.hpfilter)，来去除移动平均趋势线或周期性成分。
 
 
 
 
下面我们来执行这两种方法：
 
 
 
 
 
 
 
 
 
 
 
 
 
 
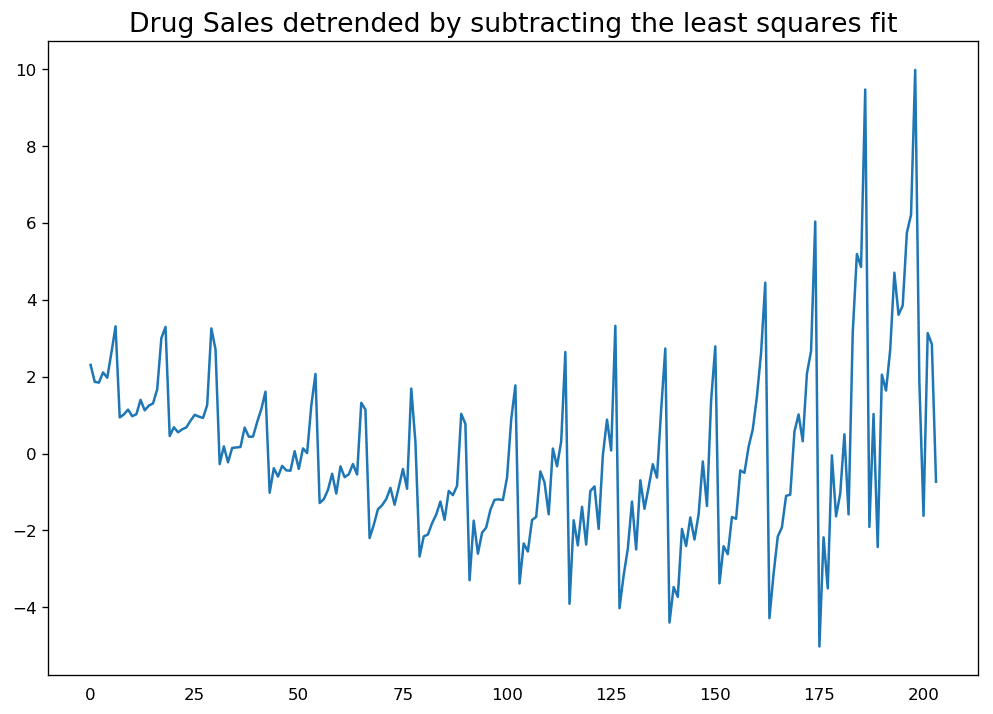
640?wx_fmt=png
 
 
通过减掉最小二乘拟合线对时间序列去趋势
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
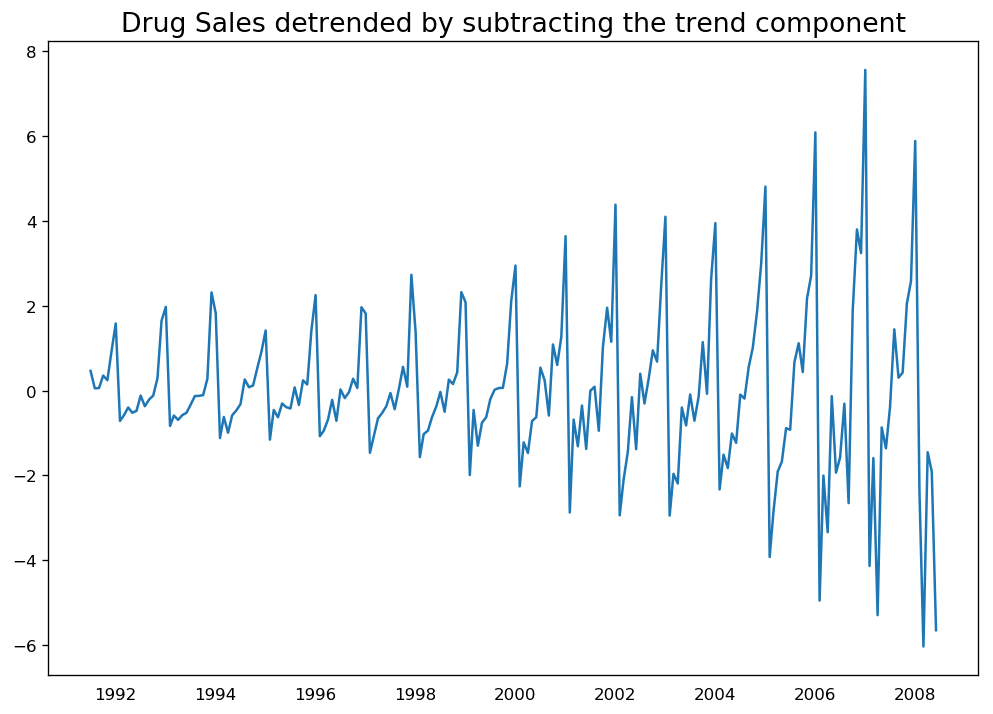
640?wx_fmt=png
 
 
通过减掉趋势成分对时间序列去趋势
 
 
 
 
 
14、如何对时间序列去季节性？
 
 
 
 
对时间序列去季节性同样有多种方法，如下：
 
 
 
 
  • 把特定长度的移动平均值作为季节窗口。
  • 对序列做季节性差分（用当前值减去上个季度的值）。
  • 用当前序列除以由 STL 分解得到的季节指数。
 
 
 
 
若除以季节指数的效果不好，可以尝试取序列的对数，然后对其去季节。之后你可以通过指数运算来恢复原来的值。
 
 
  1. # Subtracting the Trend Component.	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')	
  3.  
  4. 	
  5. # Time Series Decomposition	
  6. result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')	
  7.  
  8. 	
  9. # Deseasonalize	
  10. deseasonalized = df.value.values / result_mul.seasonal	
  11.  
  12. 	
  13. # Plot	
  14. plt.plot(deseasonalized)	
  15. plt.title('Drug Sales Deseasonalized', fontsize=16)	
  16. plt.plot
 
 
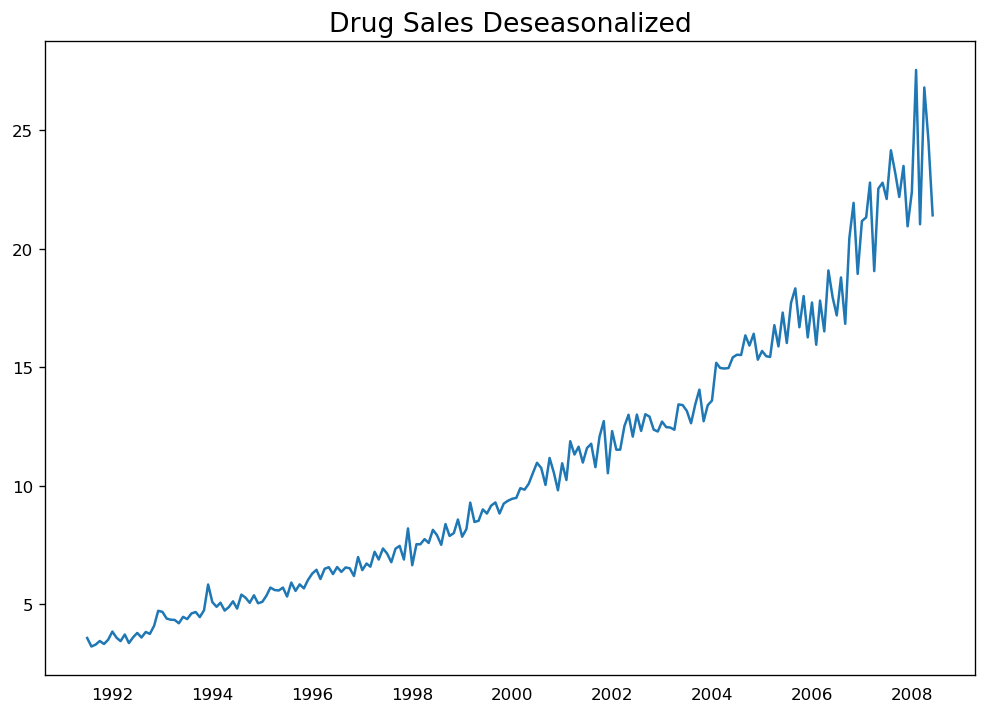
640?wx_fmt=png
 
 
对时间序列去季节
 
 
 
 
 
15、如何检测时间序列的季节性？
 
 
 
 
一般方法是画出序列图，观察固定的时间间隔是否有重复模式出现。因此，季节性的类型由时钟或日历决定：
 
 
 
 
  • 一天中的小时
  • 月份中的日期
  • 星期
  • 月份
  • 年份
 
 
 
 
不过，如果你想对季节性做一个明确的检验，可以使用自相关函数 (ACF) 图，接下来的部分会做相关详细介绍。当季节模式明显时，ACF 图中季节窗口的整数倍处会反复出现特定的尖峰。
 
 
 
 
 
例如，药品销售的时间序列是月份序列，每年会出现重复的模式，你会在第 12、24、36 个序列值处看到尖峰。
 
 
 
 
 
必须要提醒你的是，现实生活中的数据集很少会出现特别明显的模式，可能会被一些噪声污染，所以需要更加仔细观察其中的模式。
 
 
 
 
 
 
  1. from pandas.plotting import autocorrelation_plot	
  2. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')	
  3.  
  4. 	
  5. # Draw Plot	
  6. plt.rcParams.update({'figure.figsize':(9,5), 'figure.dpi':120})	
  7. autocorrelation_plot(df.value.tolist())
 
 
 
 
 
 
 
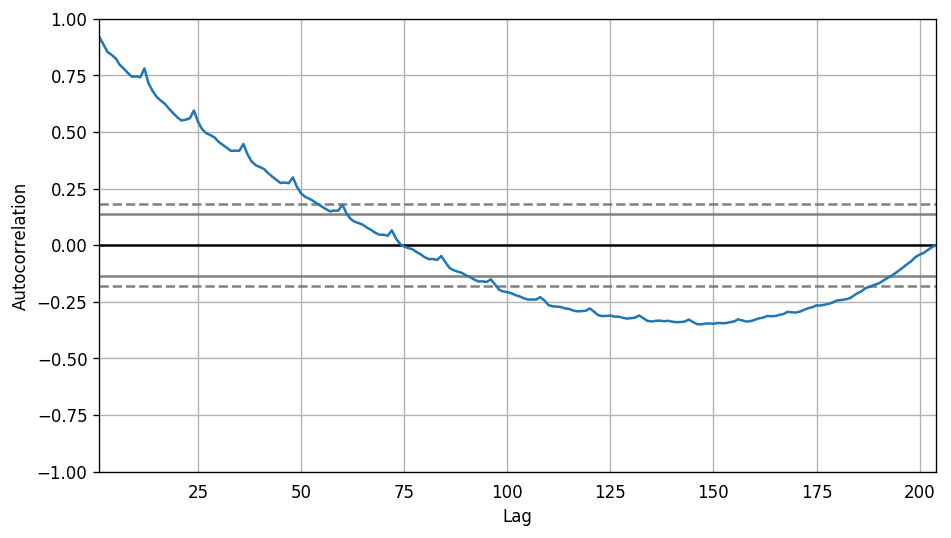
640?wx_fmt=png
 
 
自相关系数图
 
 
 
 
 
16、如果处理时间序列中的缺失值？
 
 
 
 
有时候，时间序列中会出现缺失的值或日期。这意味着，某些数据没有获取到，或者无法对这些时间段进行观测。也可能那些时间的测量值本身为零，这种情况下你只需对其填充零。
 
 
 
 
 
第二种情况，你不应该直接用序列的均值对缺失处进行填充，尤其当该序列不是平稳序列时。比较暴力但有效的解决方法是用前一个值来填充缺失处。
 
 
 
 
 
根据序列的内在属性，你可以尝试多种方法。以下是几种比较有效的填充方法：
 
 
 
 
  • 向后填充法
  • 线性插值法
  • 二次插值法
  • 最近邻均值法
  • 季节均值法
 
 
 
 
为了评估缺失值的填充效果，我在时间序列中手动加入缺失值，用以上几种方法对其进行填充，然后计算填充后的序列与原序列的均方误差。
 
 
 
 
 
 
  1. # # Generate dataset	
  2. from scipy.interpolate import interp1d	
  3. from sklearn.metrics import mean_squared_error	
  4. df_orig = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date').head(100)	
  5. df = pd.read_csv('datasets/a10_missings.csv', parse_dates=['date'], index_col='date')	
  6.  
  7. 	
  8. fig, axes = plt.subplots(7, 1, sharex=True, figsize=(10, 12))	
  9. plt.rcParams.update({'xtick.bottom' : False})	
  10.  
  11. 	
  12. ## 1. Actual -------------------------------	
  13. df_orig.plot(title='Actual', ax=axes[0], label='Actual', color='red', style=".-")	
  14. df.plot(title='Actual', ax=axes[0], label='Actual', color='green', style=".-")	
  15. axes[0].legend(["Missing Data", "Available Data"])	
  16.  
  17. 	
  18. ## 2. Forward Fill --------------------------	
  19. df_ffill = df.ffill()	
  20. error = np.round(mean_squared_error(df_orig['value'], df_ffill['value']), 2)	
  21. df_ffill['value'].plot(title='Forward Fill (MSE: ' + str(error) +")", ax=axes[1], label='Forward Fill', style=".-")	
  22.  
  23. 	
  24. ## 3. Backward Fill -------------------------	
  25. df_bfill = df.bfill()	
  26. error = np.round(mean_squared_error(df_orig['value'], df_bfill['value']), 2)	
  27. df_bfill['value'].plot(title="Backward Fill (MSE: " + str(error) +")", ax=axes[2], label='Back Fill', color='firebrick', style=".-")	
  28.  
  29. 	
  30. ## 4. Linear Interpolation ------------------	
  31. df['rownum'] = np.arange(df.shape[0])	
  32. df_nona = df.dropna(subset = ['value'])	
  33. f = interp1d(df_nona['rownum'], df_nona['value'])	
  34. df['linear_fill'] = f(df['rownum'])	
  35. error = np.round(mean_squared_error(df_orig['value'], df['linear_fill']), 2)	
  36. df['linear_fill'].plot(title="Linear Fill (MSE: " + str(error) +")", ax=axes[3], label='Cubic Fill', color='brown', style=".-")	
  37.  
  38. 	
  39. ## 5. Cubic Interpolation --------------------	
  40. f2 = interp1d(df_nona['rownum'], df_nona['value'], kind='cubic')	
  41. df['cubic_fill'] = f2(df['rownum'])	
  42. error = np.round(mean_squared_error(df_orig['value'], df['cubic_fill']), 2)	
  43. df['cubic_fill'].plot(title="Cubic Fill (MSE: " + str(error) +")", ax=axes[4], label='Cubic Fill', color='red', style=".-")	
  44.  
  45. 	
  46. # Interpolation References:	
  47. # https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html	
  48. # https://docs.scipy.org/doc/scipy/reference/interpolate.html	
  49.  
  50. 	
  51. ## 6. Mean of 'n' Nearest Past Neighbors ------	
  52. def knn_mean(ts, n):	
  53.     out = np.copy(ts)	
  54.     for i, val in enumerate(ts):	
  55.         if np.isnan(val):	
  56.             n_by_2 = np.ceil(n/2)	
  57.             lower = np.max([0, int(i-n_by_2)])	
  58.             upper = np.min([len(ts)+1, int(i+n_by_2)])	
  59.             ts_near = np.concatenate([ts[lower:i], ts[i:upper]])	
  60.             out[i] = np.nanmean(ts_near)	
  61.     return out	
  62.  
  63. 	
  64. df['knn_mean'] = knn_mean(df.value.values, 8)	
  65. error = np.round(mean_squared_error(df_orig['value'], df['knn_mean']), 2)	
  66. df['knn_mean'].plot(title="KNN Mean (MSE: " + str(error) +")", ax=axes[5], label='KNN Mean', color='tomato', alpha=0.5, style=".-")	
  67.  
  68. 	
  69. ## 7. Seasonal Mean ----------------------------	
  70. def seasonal_mean(ts, n, lr=0.7):	
  71.     """	
  72.     Compute the mean of corresponding seasonal periods	
  73.     ts: 1D array-like of the time series	
  74.     n: Seasonal window length of the time series	
  75.     """	
  76.     out = np.copy(ts)	
  77.     for i, val in enumerate(ts):	
  78.         if np.isnan(val):	
  79.             ts_seas = ts[i-1::-n]  # previous seasons only	
  80.             if np.isnan(np.nanmean(ts_seas)):	
  81.                 ts_seas = np.concatenate([ts[i-1::-n], ts[i::n]])  # previous and forward	
  82.             out[i] = np.nanmean(ts_seas) * lr	
  83.     return out	
  84.  
  85. 	
  86. df['seasonal_mean'] = seasonal_mean(df.value, n=12, lr=1.25)	
  87. error = np.round(mean_squared_error(df_orig['value'], df['seasonal_mean']), 2)	
  88. df['seasonal_mean'].plot(title="Seasonal Mean (MSE: " + str(error) +")", ax=axes[6], label='Seasonal Mean', color='blue', alpha=0.5, s
 
 
 
 
 
 
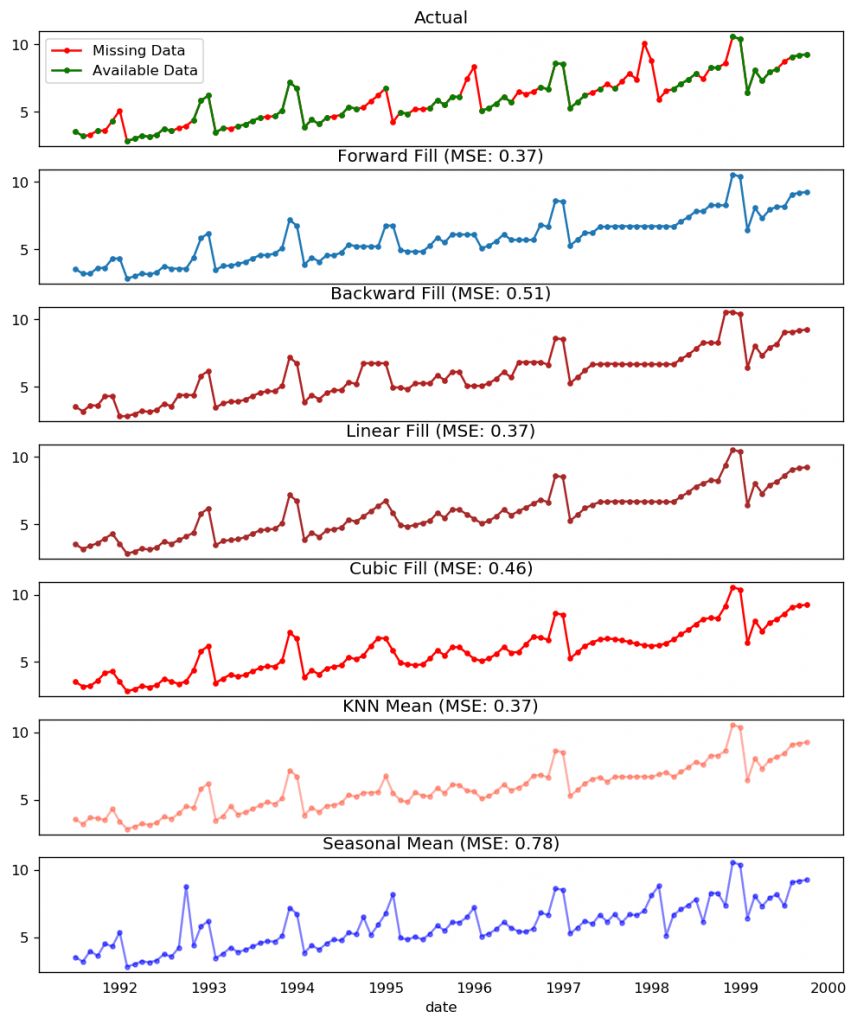
640?wx_fmt=png
 
 
缺失值处理
 
 
 
 
 
17、什么是自相关和偏自相关函数？
 
 
 
 
简单来说，自相关就是一个序列的值与自己本身具有相关性。如果一个序列呈现显著自相关，意味着序列的前一个值可用于预测当前值。
 
 
 
 
 
偏自相关也传达了类似的信息，但更偏重于序列与自身滞后序列的相关性，消除了由于较短滞后所导致的任何相关性。
 
 
 
 
 
 
  1. from statsmodels.tsa.stattools import acf, pacf	
  2. from statsmodels.graphics.tsaplots import plot_acf, plot_pacf	
  3.  
  4. 	
  5. df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')	
  6.  
  7. 	
  8. # Calculate ACF and PACF upto 50 lags	
  9. # acf_50 = acf(df.value, nlags=50)	
  10. # pacf_50 = pacf(df.value, nlags=50)	
  11.  
  12. 	
  13. # Draw Plot	
  14. fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)	
  15. plot_acf(df.value.tolist(), lags=50, ax=axes[0])	
  16. plot_pacf(df.value.tolist(), lags=50, ax=axes[1
 
 
 
 
 
 
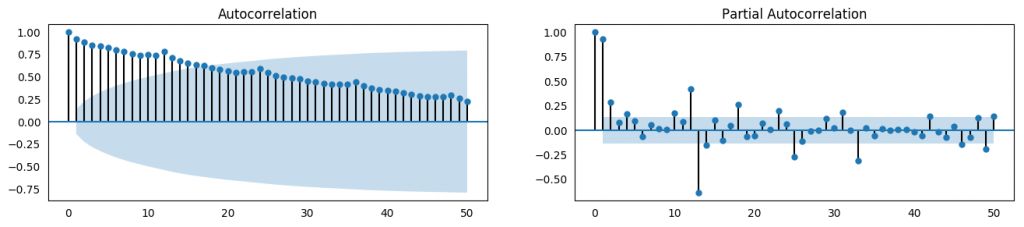
640?wx_fmt=png
 
 
ACF 和 PACF
 
 
 
 
 
18、如何计算偏自相关系数？
 
 
 
 
序列滞后 k 处的偏自相关系数是 Y 的自回归方程的滞后系数。Y 的自回归方程是指 Y 以自己的滞后作为预测因子的线性回归。
 
 
 
 
 
举个例子，如果 Y_t 为当前序列，Y_t-1 即为滞后期为 1 的 Y 值，那么滞后期为 3 处 (Y_t-3) 的偏自相关系数是下面方程中的 α3：
 
 
 
 
 
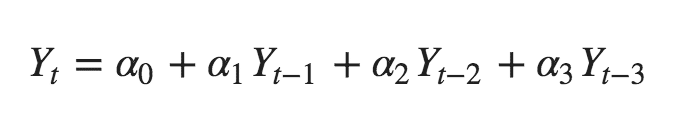
640?wx_fmt=png
 
 
自回归方程
 
 

 
 
19、滞后图
 
 
 
 
滞后图是时间序列与自身滞后的分布图，通常用来检验自相关性。如果序列中出现下图中的模式，那么说明该序列具有自相关性。如果没有出现这些模型，该序列很可能为随机白噪声。
 
 
 
 
 
在下面太阳黑子区的例子中，随着滞后期的增长，图中的点越来越分散。
 
 
  1. from pandas.plotting import lag_plot	
  2. plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})	
  3.  
  4. 	
  5. # Import	
  6. ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')	
  7. a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')	
  8.  
  9. 	
  10. # Plot	
  11. fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)	
  12. for i, ax in enumerate(axes.flatten()[:4]):	
  13.     lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick')	
  14.     ax.set_title('Lag ' + str(i+1))	
  15.  
  16. 	
  17. fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)	
  18.  
  19. 	
  20. fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)	
  21. for i, ax in enumerate(axes.flatten()[:4]):	
  22.     lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick')	
  23.     ax.set_title('Lag ' + str(i+1))	
  24.  
  25. 	
  26. fig.suptitle('Lag Plots of Drug Sales', y=1.05)	
  27. plt.sh
 
 
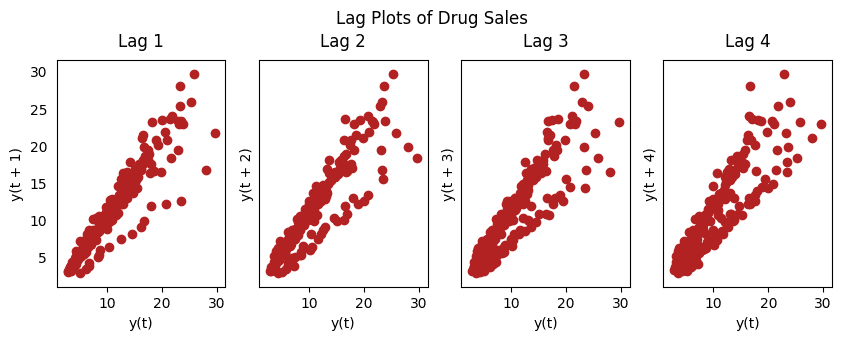
640?wx_fmt=png
 
 
药品销售滞后图
 
 
 
 
 
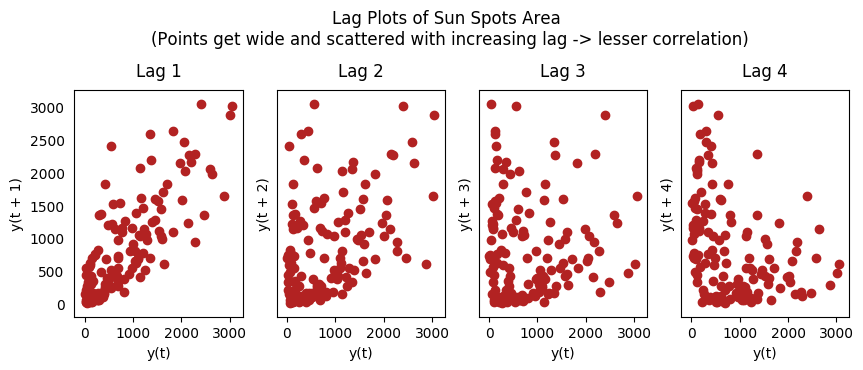
640?wx_fmt=png
 
 
太阳黑子滞后图
 
 
 
 
 
20、如何评估时间序列的可预测性？
 
 
 
 
一个时间序列的模式越有规律，就越容易预测。可以用近似熵来量化时间序列的规律性和波动的不可预测性。
 
 
 
 
 
近似熵越高，意味着预测难度越大。
 
 
 
 
 
另一个选择是样本熵。
 
 
 
 
 
样本熵与近似熵类似，但在不同的复杂度上更具有一致性，即使是小型时间序列。例如，相比于“有规律”的时间序列，一个数据点较少的随机时间序列的近似熵较低，但一个较长的随机时间序列却有较高的近似熵。
 
 
 
 
 
因此，样本熵更适于解决该问题。
 
 
 
 
 
 
  1. # https://en.wikipedia.org/wiki/Approximate_entropy	
  2. ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')	
  3. a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')	
  4. rand_small = np.random.randint(0, 100, size=36)	
  5. rand_big = np.random.randint(0, 100, size=136)	
  6.  
  7. 	
  8. def ApEn(U, m, r):	
  9.     """Compute Aproximate entropy"""	
  10.     def _maxdist(x_i, x_j):	
  11.         return max([abs(ua - va) for ua, va in zip(x_i, x_j)])	
  12.  
  13. 	
  14.     def _phi(m):	
  15.         x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]	
  16.         C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x]	
  17.         return (N - m + 1.0)**(-1) * sum(np.log(C))	
  18.     N = len(U)	
  19.     return abs(_phi(m+1) - _phi(m))	
  20.  
  21. 	
  22. print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value)))     # 0.651	
  23. print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value)))   # 0.537	
  24. print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143	
  25. print(ApEn(rand_big, m=2, r=0.2*np.std(rand_big)))     # 0. 
 
 
 
 
 
 
 
  1. 0.6514704970333534	
  2. 0.5374775224973489	
  3. 0.0898376940798844	
  4. 0.7369242960384561
 
 
 
 
 
 
  1. # https://en.wikipedia.org/wiki/Sample_entropy	
  2. def SampEn(U, m, r):	
  3.     """Compute Sample entropy"""	
  4.     def _maxdist(x_i, x_j):	
  5.         return max([abs(ua - va) for ua, va in zip(x_i, x_j)])	
  6.  
  7. 	
  8.     def _phi(m):	
  9.         x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]	
  10.         C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))]	
  11.         return sum(C)	
  12.  
  13. 	
  14.     N = len(U)	
  15.     return -np.log(_phi(m+1) / _phi(m))	
  16.  
  17. 	
  18. print(SampEn(ss.value, m=2, r=0.2*np.std(ss.value)))      # 0.78	
  19. print(SampEn(a10.value, m=2, r=0.2*np.std(a10.value)))    # 0.41	
  20. print(SampEn(rand_small, m=2, r=0.2*np.std(rand_small)))  # 1.79	
  21. print(SampEn(rand_big, m=2, r=0.2*np.std(rand_big)))      # 2.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
21、为什么要对时间序列做平滑处理？如果操作？
 
 
 
 
对时间序列做平滑处理有以下几个用处：
 
 
 
 
  • 减少噪声影响，从而得到过滤掉噪声的、更加真实的序列。
  • 平滑处理后的序列可用作特征，更好地解释序列本身。
  • 可以更好地观察序列本身的趋势。
 
 
 
 
那么如果进行平滑处理呢？现讨论以下几种方法：
 
 
 
 
  • 取移动平均线
  • 做 LOESS 平滑（局部回归）
  • 做 LOWESS 平滑（局部加权回归）
 
 
 
 
移动平均是指对一个滚动的窗口计算其平均值，该窗口的宽度固定不变。但你必须谨慎选择窗口宽度，因为窗口过宽会导致序列平滑过度。例如，如果窗口宽度等于季节长度，就会消除掉季节因素的作用。
 
 
 
 
 
LOESS 是 LOcalized regrESSion 的缩写，该方法会在每个点的局部近邻点做多次回归拟合。此处可以使用 statsmodels 包，你可以使用参数 frac 控制平滑程度，即决定周围多少个点参与回归模型的拟合。
 
 
  1. from statsmodels.nonparametric.smoothers_lowess import lowess	
  2. plt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})	
  3.  
  4. 	
  5. # Import	
  6. df_orig = pd.read_csv('datasets/elecequip.csv', parse_dates=['date'], index_col='date')	
  7.  
  8. 	
  9. # 1. Moving Average	
  10. df_ma = df_orig.value.rolling(3, center=True, closed='both').mean()	
  11.  
  12. 	
  13. # 2. Loess Smoothing (5% and 15%)	
  14. df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])	
  15. df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])	
  16.  
  17. 	
  18. # Plot	
  19. fig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)	
  20. df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')	
  21. df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')	
  22. df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')	
  23. df_ma.plot(ax=axes[3], title='Moving Average (3)')	
  24. fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)	
  25. plt.sho
 
 
640?wx_fmt=png
 
 
时间序列的平滑处理
 
 
 
 
 
22、如何用格兰杰因果关系检验判断一个时间序列是否可以预测另一个？
 
 
 
 
格兰杰因果关系检验可用作检测一个时间序列是否可以用来预测另一个序列。那么格兰杰因果关系检验是如何进行运算的呢？
 
 
 
 
 
该检验基于一个假设，即 X 导致了 Y 的发生，那么基于 Y 的先前值与 X 的先前值得到的 Y 的预测值，要优于仅根据 Y 本身得到的预测值。
 
 
 
 
 
statsmodels 包提供了便捷的检验方法。它可以接受一个二维数组，其中第一列为值，第二列为预测因子。
 
 
 
 
 
零假设为：第二列的序列与第一列不存在格兰杰因果关系。如果 P 值小于显著性水平 0.05，就可以拒绝零假设，从而知道 X 的滞后是起作用的。
 
 
 
 
 
第二个参数 maxlag 表示该检验中涉及了 Y 的多少个滞后期。
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
在上面的例子中，全部测试结果中的 P 值都为零，说明 'month' 可用作预测航班的乘客数量。
 
 
 
 
 
  
 
  
原文链接： 
 
  
https://www.machinelearningplus.com/time-series/time-series-analysis-python/
 
 
 
 
 
 
 
 
-------------------End-------------------
 
 
 
 
 
 
640?wx_fmt=jpeg
 
 
 「Python数据之道 」建立了读者交流群，大家可以添加管理员微信进行加群
 
 
640?wx_fmt=jpeg
 
 
扫描添加好友
 
 
回复 “资源”
 
 
640?wx_fmt=jpeg
 
  
 
 
 
 Python数据之道 
 
 
让数据更有价值
 
 
640?wx_fmt=jpeg
 
 
回复 “600”，
 
 
获取《Python知识手册》
 
 
 
 
640?wx_fmt=gif
 


                

        
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/144984?site
推荐阅读
相关标签
Copyright ©  2003-2013 www.wpsshop.cn  版权所有，并保留所有权利。

  
闽ICP备14008679号