机器学习之支持向量机（SVM）原理详解、公式推导（手推）、面试问题、简单实例（sklearn调包）_svm原理

1. SVM 介绍

1.1. 思路

我们先思考，我们为什么需要SVM？简单的逻辑回归线性模型它不香吗？

是的，它不香。

为什么？

1. 从解决问题的角度讲，有什么问题是SVM能轻松解决但是这哥俩死活解决不了的？
   线性不可分问题（如：异或问题）
   下图这类异或问题，线性模型就解决不了，即找不到任何一条直线能分割两类样本。我们一般有两种思路解决这个问题。一种是用感知机组成的有向图构造函数逼近器，思路是多画几条线以区分样本点，对应多层感知机；另一种就是将这些点映射到高维空间，再用超平面分割，对应支持向量机。

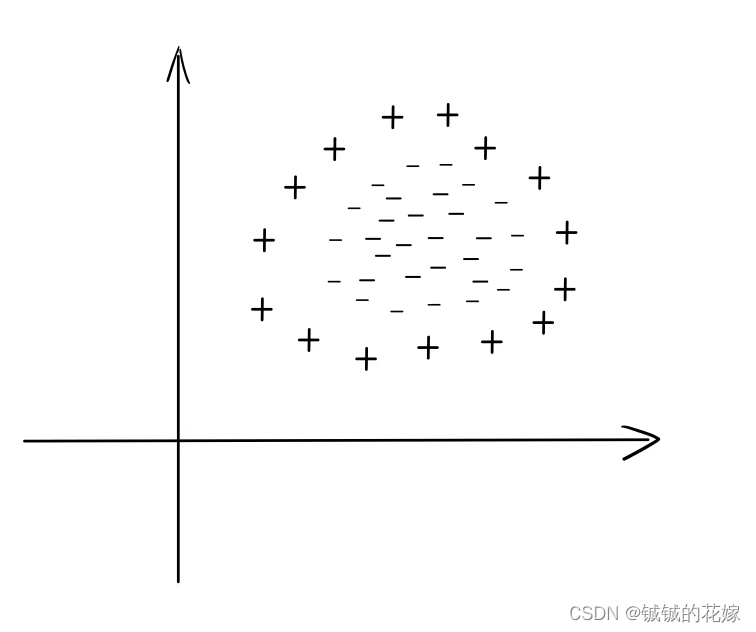
2. 从更好的解决问题的角度讲，SVM具有啥优势？
   更好的泛化能力
   我们可以看到，SVM找到的超平面拥有强大的泛化能力，对于可能出现的新的接近划分平面的样本点（蓝色标注点）的分类能力强于另外两种方法，因为线性模型很难保证每次都取到距离所有点都很远的划分线。

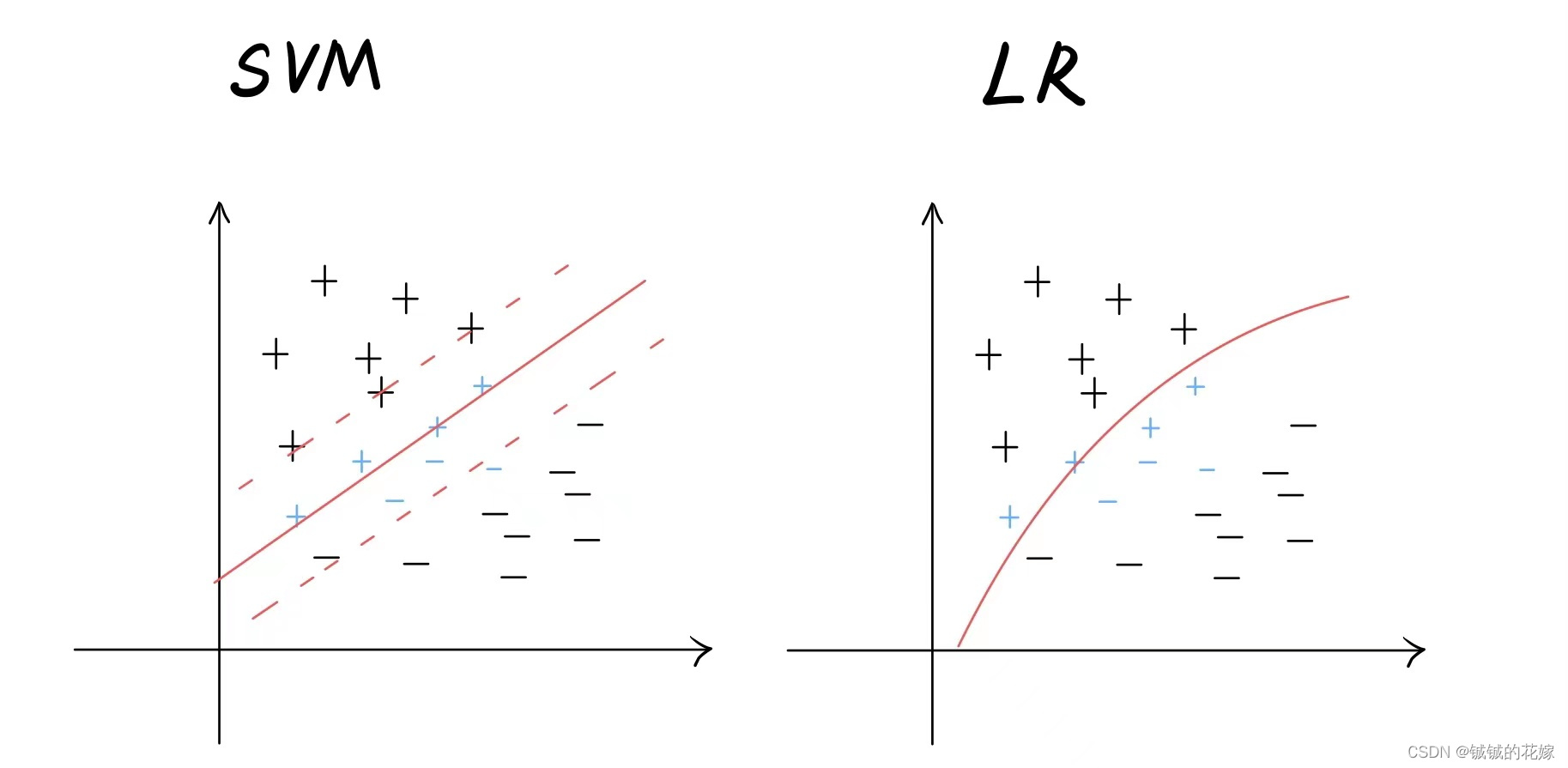
我们之前提到支持向量机会把样本点映射到高维空间，那这个是怎么做到的呢？

这里就需要引入核函数，它的主要功能就是这个，几种比较常见的核函数如下：

说到这里我们发现其实我们已经能解决问题了，但是有点时候有些数据它就是难看，我们很难找到一组非常合适的支持向量来支撑我们的超平面，这个时候我们就想到了引入软间隔和正则化。也正是因为存在软间隔，支持向量机才会出现松弛变量和对应的损失计算。

1.2. 特性

SVM说实话能做的事情挺多的，sklearn官网上就提到了分类、回归、异常值检测。优点也很明确：

• 高维空间表现好（毕竟是靠超平面划分的）
• 在样本数大于维数时表现依旧很好（个人理解是因为在SVM中大多数的样本是用不到的，只有小部分样本会被拿过来当支持向量，因此比较适应小样本的环境）
• 内存友好（因为超平面是由 几个 支持向量撑起来的，所以不需要占很大的内存空间）
• 多样性（核函数很多种多样，甚至有些核对应特定问题）

缺点也有：

• 样本数远小于特征数的时候，需要仔细选择核函数和回归类型
• SVM不会直接给出概率估计，如果真的需要，那可以用交叉验证，但是显然这样会消耗大量资源

2. 前置知识

在推导SVM之前，我们得先拣一拣忘光的数学知识。我这里只是提炼出这几个知识点中的结论，够用就好，如果想要彻底了解这几个知识点的基本原理和推导过程，还需要读者额外参考其他资料。

2.1. 超平面

关于SVM，我们需要对于超平面有最基本的认识，包括但不限于以下3点。

• 超平面的表达
• 超平面计算距离
• 超平面的正反

n维空间下的超平面表达式：
$$w^{T}x+b=0$$
其中w和x为n维向量，w = ($w_1$;$w_2$;…;$w_n$) 代表n维空间的法向量，决定超平面的方向，x代表超平面内的点，b代表位移项。实在不理解可以带入到三维空间想想。

超平面计算距离的方法很简单，超平外的一点 x 到超平面 (w,b) 的距离为：
$$r=\frac{|w^{T}x+b|}{\Vert w\Vert }$$
上式中的 $\Vert w\Vert$ 为一个L2范数，
$$\Vert w\Vert =\sqrt{\sum _{i=1}^n{w}_i^2}$$

超平面的正反意味着x点与超平面间的关系：
x 在超平面的 { 正面 , w T x + b > 0 平面上 , w T x + b = 0 背面 , w T x + b < 0 x在超平面的\left\{

$$\begin{array}{rcl} 正面 & & ,w^Tx+b>0\\ 平面上 & & ,w^Tx+b=0\\ 背面 & & ,w^Tx+b<0\\ \end{array}$$ \right. x在超平面的⎩ ⎨ ⎧​正面平面上背面​​,wTx+b>0,wTx+b=0,wTx+b<0​

我只是浅浅总结一下，主要参考这篇的，如果有小伙伴看不懂，可以去逛逛。

2.2. 拉格朗日乘子法

拉格朗日乘子法完全还给高数老师的看这里，题主讲的很不错，醍醐灌顶。

我这边浅浅总结下要用的几个点，主要强调解决这个问题的方法，基本原理和想法这里不做要求。

整体思路是面对多元函数求极值问题时，通过引入拉格朗日乘子a个变量b个约束条件的问题转化为a+b个变量无约束的问题，然后优化求解。

这个时候我们就应该考虑约束条件了，约束条件一般分为两种——等式约束和不等式约束。

等式约束

我们有目标函数和约束条件：
$$\begin{gathered} minf(x) \\ s.t.g(x)=0 \end{gathered}$$
那我们定义拉格朗日函数：
$$L(x,\lambda )=f(x)+\lambda g(x)$$
分别对$L(x,\lambda )$的$x,\lambda$的偏导置零，将变量转化为条件。目标其实就是求$L(x,\lambda )$的极值。

不等式约束

我们有目标函数和约束条件：
$$\begin{gathered} minf(x) \\ s.t.g(x)\le 0 \end{gathered}$$
定义拉格朗日函数：
$$L(x,\lambda )=f(x)+\lambda g(x)$$
约束条件转化为KKT条件：
{ g ( x ) ≤ 0 λ ≥ 0 λ   g ( x ) = 0 \left\{

$$\begin{array}{rcl} g(x)\le0\\ \lambda\ge0\\ \lambda \ g(x)=0\\ \end{array}$$ \right. ⎩ ⎨ ⎧​g(x)≤0λ≥0λ g(x)=0​
问题转化为在KKT条件下求解$L(x,\lambda )$的最小值。

2.3. 对偶问题

拉格朗日里面有个对偶问题，这里需要提一下，不然后面公式推导会有问题。我们通俗的讲就是这样的：

我需要物色我的男朋友

原问题：我要在一群高个的男生中挑一个最挫的。$ma{x}_{\alpha \beta }(mi{n}_{x}f(x,\alpha ,\beta ))$
对偶问题：我要在一堆挫的中间挑一个个最高的。$mi{n}_x(ma{x}_{\alpha \beta }f(x,\alpha ,\beta ))$

那在一般情况下，我按照这俩条件挑的最佳男友的评分不就是（用公式理解一下）
$$原问题\ge 对偶问题$$
这个就是弱对偶问题。

如果碰巧这个男生既是最高的又是最挫的，那这个时候
$$原问题=对偶问题$$
这个就是强对偶问题。

那什么时候弱对偶问题能转化为强对偶问题？

我们变回数学语言，那就是下面三个约束条件：

• 原问题是凸函数
• $g(x)$是线性约束（$a_{i}x+b<0$）
• 满足KKT条件

3. 原理推导

3.1. 公式推导

我们首先得到支持向量机的基本型。

3.2. 求解

参考西瓜书的思路，我们这里的求解也分为两部分，第一部分是利用拉格朗日乘子法和对偶问题问题转化为一个给定约束条件求目标函数最大值的问题。第二部分我们利用SMO算法迭代找到最优解，这里我们不考虑SMO算法的剪枝。

3.2.1. 转化对偶问题

条件数不够，直接求解做不了，所以我们用拉格朗日乘子法转化一下问题。

3.2.2. SMO算法

SMO算法与启发式算法的想法相似，在面对n个变量的问题的时候选择固定一个变量，一个一个推导，但是在SVM这部分推导时不能直接这么做，为什么？

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$
因为上述约束条件决定了如果只有一个变量，则可以直接推出：
$${\alpha }_1{y}_1=-\sum _{i=2}^m{\alpha }_i{y}_i$$
无法解决问题，因此我们在SMO算法中固定两个变量${\alpha }_1{\alpha }_2$，以此计算 $\alpha$ 的推导式。

4. 核函数与软间隔

这部分是SVM的精髓，但是博主目前能力有限，这部分的数学公式推导还没有完全搞明白，未来可能会出相关的推导博文，这里就先混着公式浅浅总结下。

我们之前推导的SMO算法等都是在线性约束条件下的，但是面对非线性问题以及一些线性不可分的问题的时候，我们还是需要核函数映射一下的，把非线性问题转化为线性问题求解。

4.1. 核函数

非线性问题的求解大概分两步：

1. 把非线性问题在高维空间转化为线性问题
2. 找到对应的核函数，在求解时把高维的问题在低维下求解

大概推了下，解释下上面俩步骤：

上图举例的核函数是多项式核函数：
$$(x_i\cdot x_j{)}^{d}d\ge 1$$
下面再浅浅解释一下高斯核函数的一些特性

4.2. 软间隔

SVM因为支持向量的选取的原因，很容易受噪声干扰，在现实中很容易因为部分样本导致支持向量间距过窄。这个时候我们引入软间隔，允许部分样本在间隔内。两者对比图如下。

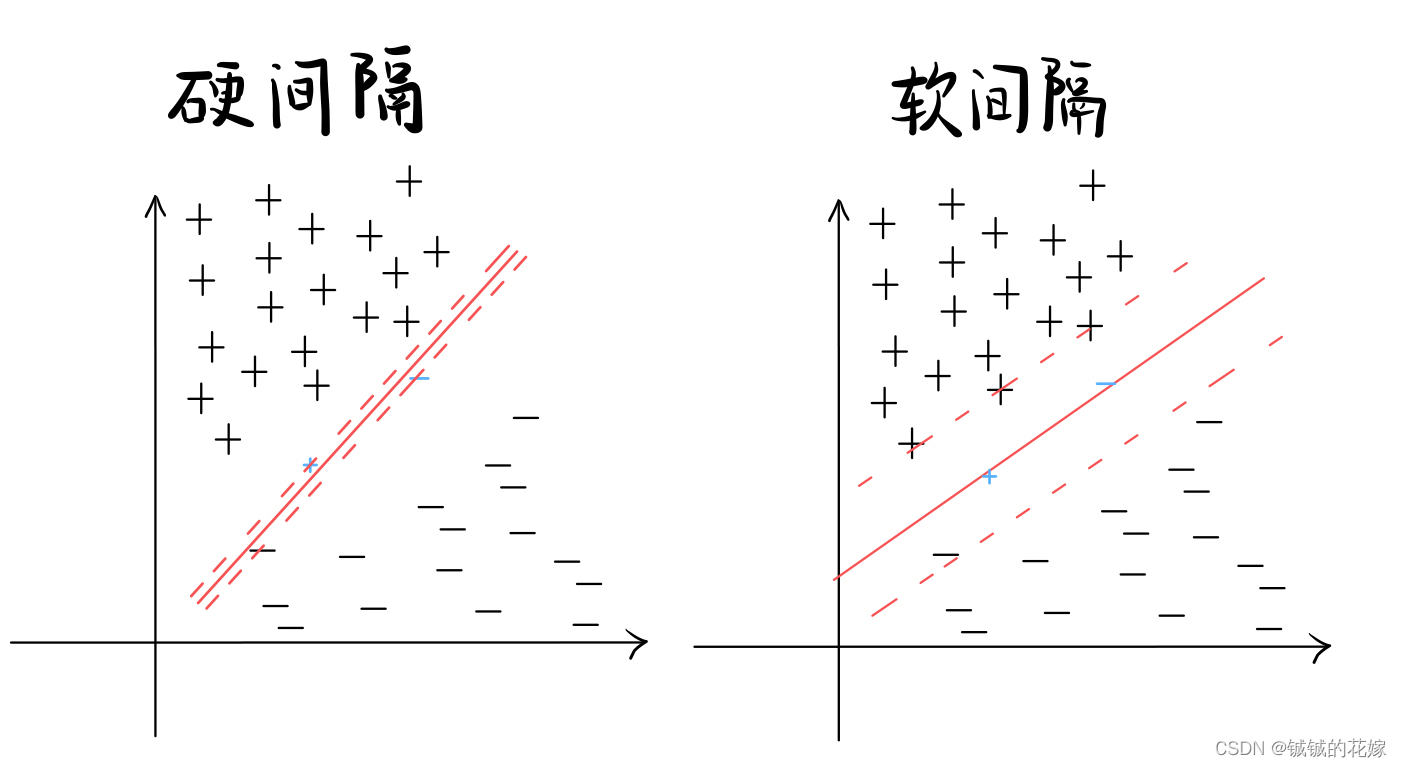
关于软间隔的几个点提一下，主要是有几个概念：

5. 几个注意点(面试问题)

  支持向量机有几个注意点，可能会在面试中被提到，还是比较能体现被面试者对这个算法的理解的。当然我们也不一定就是为了面试，搞清楚这些问题对帮助我们理解这个算法还是很有好处的。其中部分答案是博主自己的理解，如果有问题请路过的大佬评论区指正。

1. 是不是所有分类问题逻辑回归都能解决？如果不能，那还有什么其他思路吗？

答：

显然不是，线性不可分的问题逻辑回归都不能解决，如：异或问题。一般来说这种问题还有两种方法解决：1. 用感知机组成的有向图构造函数逼近器。2. 映射到高维空间中解决。支持向量机就是这个思路。

异或问题图如下，我们可以发现很难找到一条线可以很好的区分这四个点的。

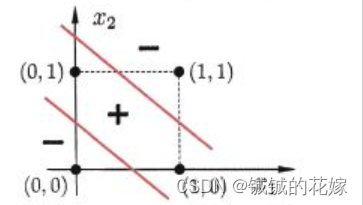
支持向量机的想法就是打算把这个二维的图映射到高维空间上，并找到一个可行的平面，如下图所示。

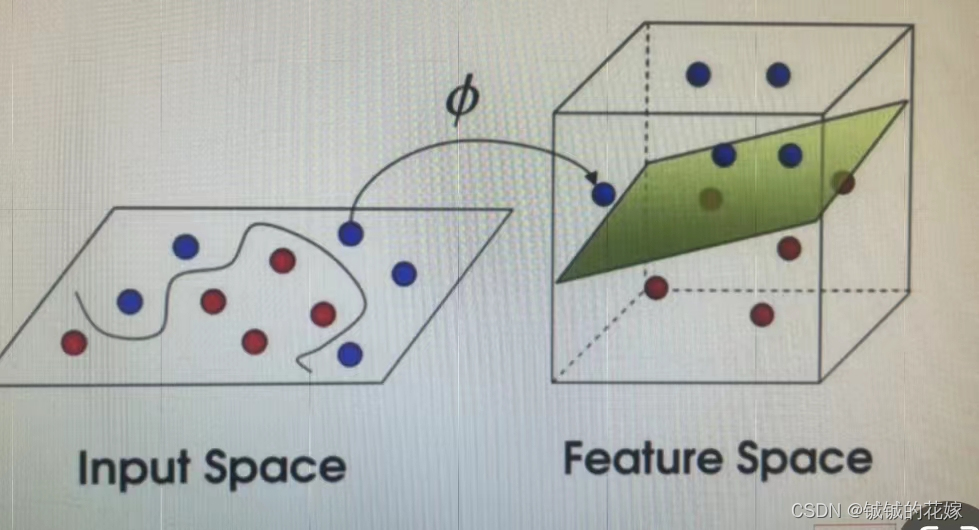
2. 支持向量机的基本思路？

答：

上面都讲了，这里不赘述。

3. 支持向量机能否用于特征选择？效果如何？

答：

能，但是效果并不理想。

4. 支持向量机中的“支持”应该怎么理解？

答：

支持向量机的思路是在样本空间中找到出一个划分的超平面，这个超平面是由很多个边界的点（支持向量）支撑起来的，所谓“支持”就是这些通过这些支持向量撑起一个最佳的划分超平面。

5. 在支持向量机中是否所有的样本都是有效的？

答：

不是，支持向量机中只有支持向量那几个样本是有效的，因为超平面的划分只跟这几个样本有关，跟其他样本无关。

7. 讨论线性判别分析（LDA）和线性核支持向量机（SVM）在何种条件下等价？

答：

• LDA针对多分类问题，SVM针对二分类问题（当然n分类也不是不可以做）。
• LDA看重同类点间方差最低和不同类样本中心间隔最大，然后投射到一条直线上，这跟SVM也不一样。

因此，在二分类和数据线性可分问题时，两者等价。

8. 高斯核SVM核RBF神经网络之间的联系？

答：

SVM 的确与神经网络有密切联系：若将隐层神经元数设置为训练样本数，且每个训练样本对应一个神经元中心，则以高斯径向基函数为激活函数的RBF网络恰与高斯核SVM的预测函数相同。（p145《休息一会儿》）出处

9. 为什么SVM对噪声敏感？

答：

SVM在硬间隔的情况下对噪声十分敏感，因为本质上SVM分类器是一开那几个支持向量划分平面的，一旦支持向量中存在噪声点，就会导致分类器划分的依据中掺杂含有噪声的数据，导致划分不当。噪声也可能导致模型的泛化能力变差，因为如果噪声点因为满足划分条件被划对了，这会压缩划分超平面时两端的间距，在使用模型时，泛化能力差。从结果导向来看，正是因为噪声对模型的影响过大，才出现了后来的软间隔方法来减少噪声对其的影响。

10. 在空间上线性可分的两类点，分别向SVM分类的超平面上做投影，这些点在超平面上的投影仍然是线性可分的吗？

答：

当然不，下面我分 3 部分解释这个命题。
1 举反例
  我们将问题简化为二维的，那么超平面将退化为一条线。那么，这些投影不一定是线性可分的结果如下：

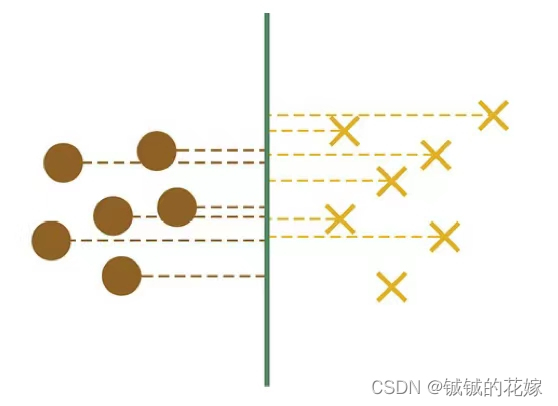
2 反证法
  我们进一步用反证法证明这一组点的投影都是线性不可分的。因为支持向量机中的超平面仅仅由支持向量决定，所以我们考虑只有支持向量的情况。在二维的情况下，假设这些点的投影是线性可分的，那么我们得到这样一个图。1号线为两组点的超平面，这两组点在这个平面上的投影线性可分。

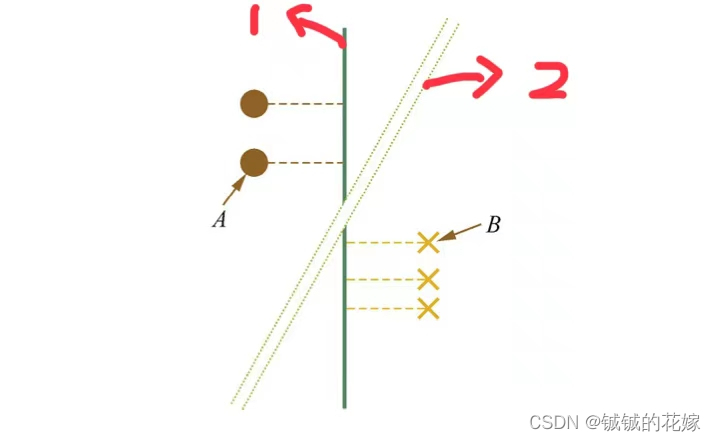
  但是，如果这两组点是一批支持向量的话，那么显然 AB 的中垂线 2号线更适合作为超平面，，是更优的超平面的解，在这个超平面中，这两组点显然是线性不可分的。
  在证明是基于在超平面换了之后，支持向量不变的情况下的，如果要严谨证明的话，那还要说明为什么超平面换了之后，支持向量不会改变，即SVM的结果仅仅依赖支持向量。我的建议是把这个当作结论来记，证明需要联系KKT条件（ $g_i(w^{\ast })<0$ 时必有 $a_i^{\ast }=0$ ）和拉格朗日对偶优化问题公式（ $g_i(w^{\ast })=-y_i(w^{\ast }\cdot x_i+{\beta }^{\ast })+1$ ），色到出支持向量外，其他系数都为零，即SVM的分类结果仅仅依靠支持向量。

3 超平面分离定理（SHT）
  对于这个问题，SHT定理是一条捷径，这个定理描述的是对于两个不相交的凸集，存在一个超平面将两个凸集分离。那么对于二维的情况，这个超平面就是两个凸包上最短的两点的连线的中垂线。接下来就是分类讨论凸包上最近的两个点的关系了。

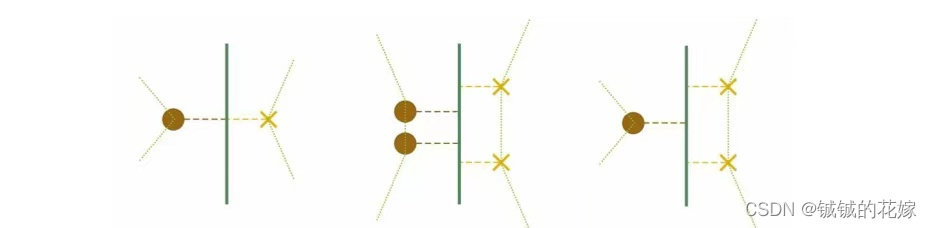
  无论哪种情况，都是线性不可分的。

11. 是否存在一组参数使得SVM训练误差为0？

答：

在所有样本的类别都被正确预测时，训练误差为0。证明我不太会，大概思路时在高斯核SVM中把$||f(x^{(j)})-y^{(j)}||\le {\sum }_{i=1,i\ne j}^m{e}^{-||f(x^{(j)})-x^{(i)}|{|}^2/{\gamma }^2}$ 放缩到 ${\sum }_{i=1,i\ne j}^m||e^{-logm}||$=$(m-1)/m<1$，这意味着预测结果与真实结果相差小于1，所以 $y^j=1$时，$f(x^{(j)})>0$；$y^j=-1$时，$f(x^{(j)})<0$。这时可以发现所有样本类别都被正确预测时，训练误差=0。

12. 一定存在训练误差为0的SVM分类器吗？

答：

一定。联系上一个问题，这个问题时找到一个参数可以使得误差=0且为SVM模型的一个解。在SVM中 $y^{(i)}\cdot f(x^{(j)})\ge 1$，所以接下来我们的目标是在上给问题的基础上多证明 $y^{(i)}\cdot f(x^{(j)})\ge 1$ 这个条件。
把预测公式 $f(x)={\sum }_{i=1}^m{\alpha }_i{y}^{(i)}K(x^{(i)},x)$ 代入限制条件中，化简得到$y^{(i)}\cdot f(x^{(j)})={\alpha }_j+{\sum }_{i=1}^m{\alpha }_i{y}^{(i)}{y}^{(j)}K(x^{(i)},x^{(j)})$，如果 ${\alpha }_j$ 大，$\gamma$ 小，那么 $K(x^{(i)},x^{(j)})$ 就很小很小，那么 $y^{(i)}\cdot f(x^{(j)})$ 将完全由 ${\alpha }_j$ 决定，很容易达到 $y^{(i)}\cdot f(x^{(j)})\ge 1$。

13. 加入松弛变量之后的SVM的训练误差可以为0吗？

答：

不一定。因为惩罚系数C为一个未知常数，所以这个问题还是有点疑惑的点的。SMO算法的线性分类器不一定的发哦训练误差=0的模型，因为我们的算法目标改变了，相比于训练误差最小，有点训练误差但是参数较小的点将会更受青睐。
特例：C=0时，w=0也能达到优化目标，但是此时显然我们的训练误差不一定=0。

14. 不是所有的非线性问题都可以通过SVM解决？

答：

是的。如果打一个数据集$x_i$映射到无限维，那一定可以找到一个维度中，这个问题是线性可分的，只不过求解的时候计算量非常大，会比较慢。

6. 代码详解

6.1. sklearn SVM

二分类问题和多分类问题都可以用SVC, NuSVC 和 LinearSVC完成，我们一一尝试。这边不详细解释原理，细究可以查看官网。SVC和NuSVC相似，LinearSVC在线性核下更快

def package_SVM(data, label):
    print("SVC")
    # 建模
    # 默认是rbf核函数，可以改poly,linear,sigmoid,precomputed核；
    # 还有正则化参数还算重要的
    # 很多svc的参数都跟特定问题相关，比如coef0就只在poly,sigmoid核下比较重要
    # 乳腺癌这个问题比较简单，我就一路默认过去了
    svc = SVC(random_state=1129)
    # 训练（这里使用交叉验证）
    score = cross_val_score(svc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))

    print("NuSVC")
    # 跟SVC相似，但是使用了一个参数去控制支持向量的数量
    nusvc = NuSVC(random_state=1129)
    # 训练（这里使用交叉验证）
    score = cross_val_score(nusvc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))

    print("LinearSVC")
    # 类似线性核下的svc，但是选惩罚函数和损失函数时更灵活，也能更好的扩展到大样本数据中
    # 有penalty(l1, l2), loss(hinge, squared_hinge)参数，不建议l1 和 hinge组合
    linearsvc = LinearSVC(random_state=1129)
    score = cross_val_score(linearsvc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

效果如下：

7. 代码实现（可直接食用）

import collections
import random
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC, NuSVC, LinearSVC
from sklearn.model_selection import train_test_split, cross_val_score


def try_SVM(dataset):

    pass


def package_SVM(data, label):
    print("SVC")
    # 建模
    # 默认是rbf核函数，可以改poly,linear,sigmoid,precomputed核；
    # 还有正则化参数还算重要的
    # 很多svc的参数都跟特定问题相关，比如coef0就只在poly,sigmoid核下比较重要
    # 乳腺癌这个问题比较简单，我就一路默认过去了
    svc = SVC(random_state=1129)
    # 训练（这里使用交叉验证）
    score = cross_val_score(svc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))

    print("NuSVC")
    # 跟SVC相似，但是使用了一个参数去控制支持向量的数量
    nusvc = NuSVC(random_state=1129)
    # 训练（这里使用交叉验证）
    score = cross_val_score(nusvc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))

    print("LinearSVC")
    # 类似线性核下的svc，但是选惩罚函数和损失函数时更灵活，也能更好的扩展到大样本数据中
    # 有penalty(l1, l2), loss(hinge, squared_hinge)参数，不建议l1 和 hinge组合
    linearsvc = LinearSVC(random_state=1129)
    score = cross_val_score(linearsvc, data, label, cv=5)
    print("%0.4f accuracy with a standard deviation of %0.4f" % (score.mean(), score.std()))



if __name__ == '__main__':
    random.seed(1129)
    data = load_breast_cancer(as_frame=True).data
    label = load_breast_cancer(as_frame=True).target
    # 标准化一下数据，方便计算
    data = StandardScaler().fit_transform(data)
    X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.2, random_state=1129)
    dataset = (X_train, X_test, y_train, y_test)
    choice = 0
    while choice != 3:
        print("0. 查看数据\n1. 手写SVM\n2. 调包SVM\n3. 退出")
        try:
            choice = int(input())
        except:
            break
        if choice == 0:
            print("特征数据：\n", data)
            print(data.shape)
            print("标签数据：\n", label)
            print(dict(collections.Counter(label)))
        elif choice == 1:
            print("手写SVM求解中...")
            try_SVM(dataset)
        elif choice == 2:
            print("调包SVM求解中...")
            package_SVM(data, label)
        else:
            print("退出成功")
            choice = 3
            break


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

参考：
吴恩达《机器学习》
《百面机器学习.》