朴素贝叶斯/SVM/LDA主题模型_lda仿真算法测试

一. 朴素贝叶斯
在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。对于大多数的分类算法，比如决策树,KNN,逻辑回归，支持向量机等，他们都是判别方法， 也就是直接学习出特征输出Y和特征X之间的关系，要么是决策函数Y=f(X),要么是条件分布P(Y|X)。 但是朴素贝叶斯却是生成方法，也就是直接找出特征输出Y和特征X的联合分布P(X,Y),然后用P(Y|X)=P(X,Y)/P(X)得出。
1.朴素贝叶斯公式

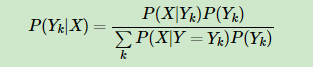
2.朴素贝叶斯的模型
从统计学知识回到我们的数据分析。假如我们的分类模型样本是：

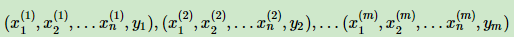
即我们有m个样本，每个样本有n个特征，特征输出有K个类别，定义为C1,C2,…,CK。 从样本我们可以学习得到朴素贝叶斯的先验分布P(Y=Ck)(k=1,2,…K), 接着学习到条件概率分布P(X=x|Y=Ck)=P(X1=x1,X2=x2,…Xn=xn|Y=Ck),然后我们就可以用贝叶斯公式得到X和Y的联合分布P(X,Y)了。联合分布P(X,Y)定义为：

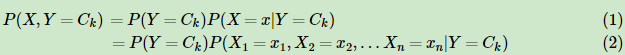
从上面的式子可以看出P(Y=Ck)比较容易通过最大似然法求出，得到的P(Y=Ck)就是类别Ck在训练集里面出现的频数。但是P(X1=x1,X2=x2,…Xn=xn|Y=Ck)很难求出,这是一个超级复杂的有n个维度的条件分布。朴素贝叶斯模型在这里做了一个大胆的假设，即X的n个维度之间相互独立，这样就可以得出:从上面的式子可以看出P(Y=Ck)比较容易通过最大似然法求出，得到的P(Y=Ck)就是类别Ck在训练集里面出现的频数。 但是P(X1=x1,X2=x2,…Xn=xn|Y=Ck)很难求出,这是一个超级复杂的有n个维度的条件分布。朴素贝叶斯模型在这里做了一个大胆的假设，即X的n个维度之间相互独立，这样就可以得出:

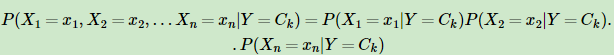
最后回到我们要解决的问题，我们的问题是给定测试集的一个新样本特征，我们如何判断它属于哪个类型？ 既然是贝叶斯模型，当然是后验概率最大化来判断分类了。我们只要计算出所有的K个条件概率P(Y=Ck|X=X(test)),然后找出最大的条件概率对应的类别，这就是朴素贝叶斯的预测了。

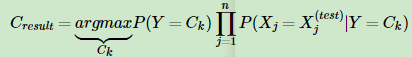
3.朴素贝叶斯算法小结
朴素贝叶斯算法的主要原理基本已经做了总结，这里对朴素贝叶斯的优缺点做一个总结。 朴素贝叶斯的主要优点有：
（1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
（2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
（3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：　
（1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
（2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
（3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
（4）对输入数据的表达形式很敏感。
4.朴素贝叶斯训练/建模

• 高斯分布型：用于classification问题，假定属性/特征是服从正态分布的。
• 多项式型：用于离散值模型里。比如文本分类问题里面我们提到过，我们不光看词语是否在文本中出现，也得看出现的次数。如果总词数为n，出现词数为m的话，说起来有点像掷骰子n次出现m次这个词的场景。
• 伯努利型：这种情况下，就如之前博文里提到的bag of words处理方式一样，最后得到的特征只有0(没出现)和1(出现过)。

# 我们直接取iris数据集，这个数据集有名到都不想介绍了...
# 其实就是根据花的各种数据特征，判定是什么花
from sklearn import datasets
iris = datasets.load_iris()
iris.data[:5]
#array([[ 5.1,  3.5,  1.4,  0.2],
#       [ 4.9,  3. ,  1.4,  0.2],
#       [ 4.7,  3.2,  1.3,  0.2],
#       [ 4.6,  3.1,  1.5,  0.2],
#       [ 5. ,  3.6,  1.4,  0.2]])

#我们假定sepal length, sepal width, petal length, petal width 4个量独立且服从高斯分布，用贝叶斯分类器建模
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
right_num = (iris.target == y_pred).sum()
print("Total testing num :%d , naive bayes accuracy :%f" %(iris.data.shape[0], float(right_num)/iris.data.shape[0]))
# Total testing num :150 , naive bayes accuracy :0.960000

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

5.朴素贝叶斯之文本主题分类器
这是朴素贝叶斯最擅长的应用场景之一，对于不同主题的文本，我们可以用朴素贝叶斯训练一个分类器，然后将其应用在新数据上，预测主题类型。