C++ 树进阶系列之笛卡尔树的两面性_c++ 笛卡尔树

1. 前言

笛卡尔树是一种特殊的二叉树数据结构，融合了二叉堆和二叉搜索树两大特性。笛卡尔树可以把数列(组)对象映射成二叉树，便于使用笛卡尔树结构的逻辑求解数列的区间最值或区间排名等类似问题。

如有数列 {5,7,1,9,12,16,2,18,3,11}，任一存储单元格均有 2 个属性：

• 值：单元格中的数据。
• 位置：单元格在数列中的位置（下标、索引）。

构建笛卡尔树要求节点至少有 2 个权重，把数列映射成树结构时，可使用这2 个属性作为笛卡尔树节点的权重。把线性结构的数列映射成笛卡尔树后，此树需要满足如下 2 个特征：

• 如果观察值，则在树中具有堆的有序性，即任一父节点的值大于（最大堆）或小于（最小堆）子节点的值。根据堆的特性，可以查询笛卡尔树或子树上的最大值或最小值。且可以使用堆排序算法排序数列。

• 如果观察位置，则在树中遵循搜索树的逻辑结构，或者说，对笛卡尔树进行中序遍历，可以得到原来的数组。

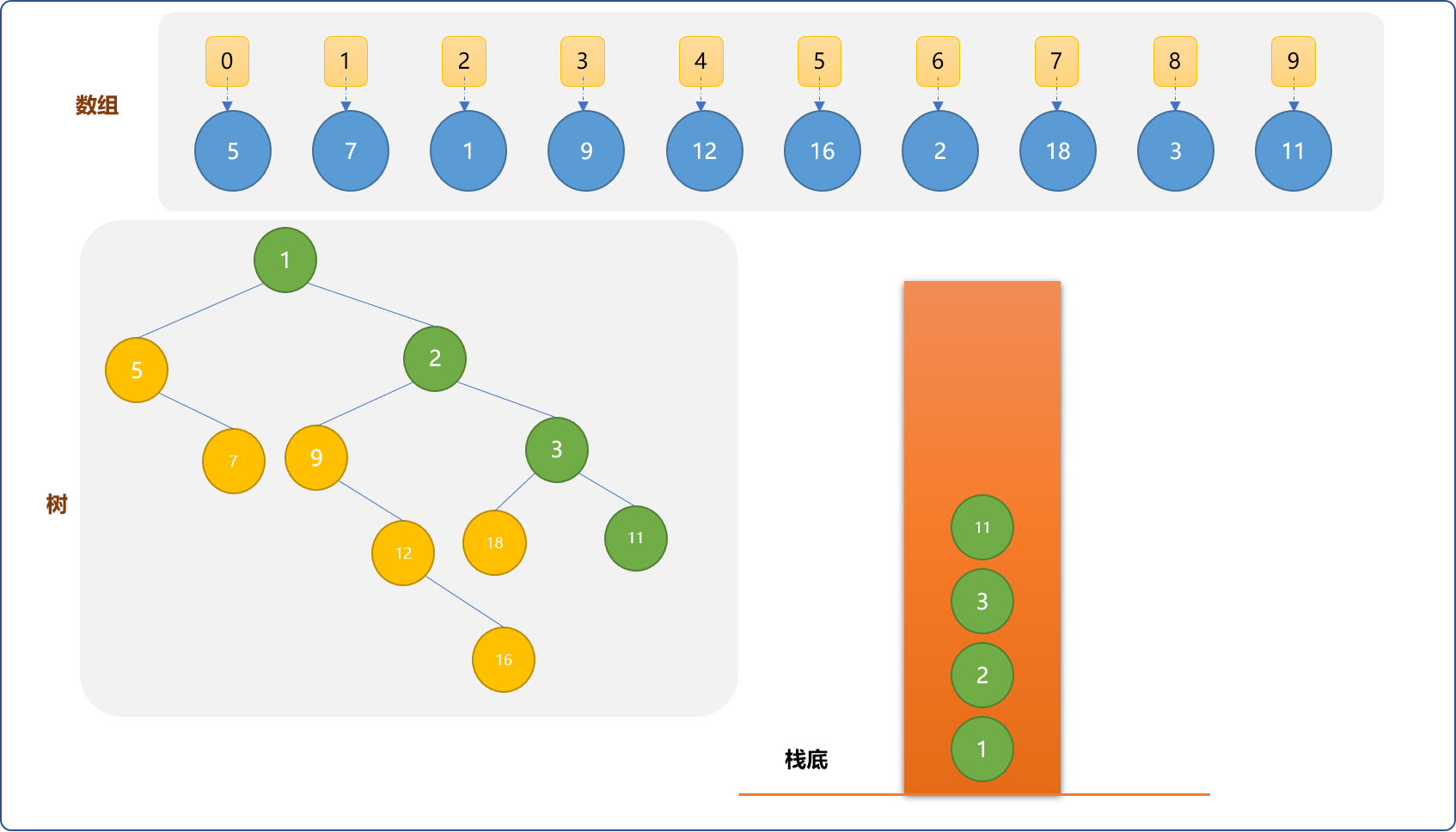
2. 构建笛卡尔树

可以说笛卡尔树是双权重的节点树。那么，如何构建才能保证数列最终能映射成笛卡尔树。

实现过程中，需要借助单调栈数据结构。

什么是单调栈？

本质指的就是栈，但在存储数据时，需要要保持栈中数据按递增或递减顺序，本文构建最小堆，要求栈单调递减。

2.1 构建流程

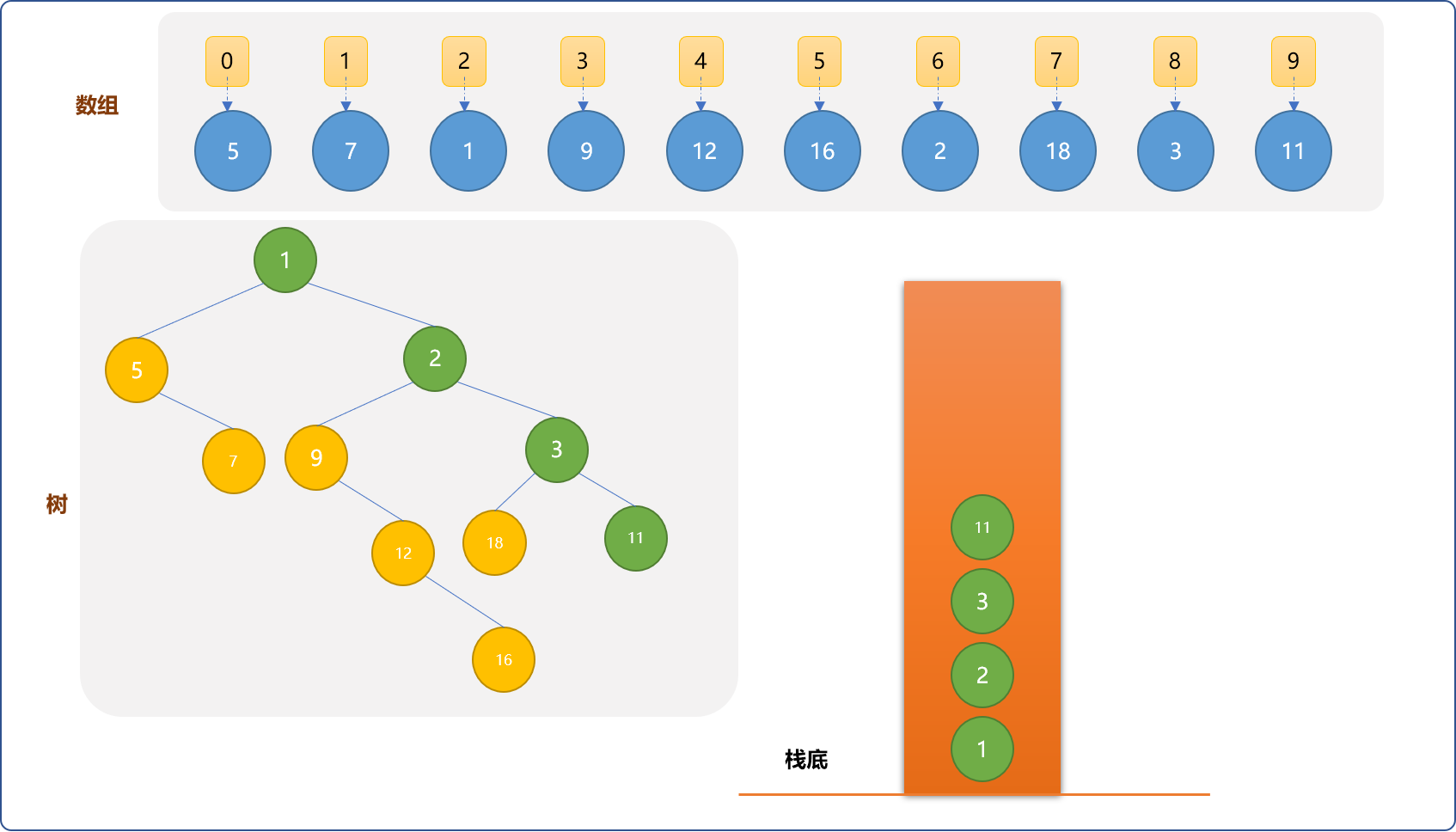
现把数组 {5,7,1,9,12,16,2,18,3,11}构建成笛卡尔树的过程详细讲解一下：

• 首先，准备一个栈。把数组中位置为 0、值为5 的元素（后面统一以(0,5)格式描述）。将其压入栈中，且设置成树的根节点。

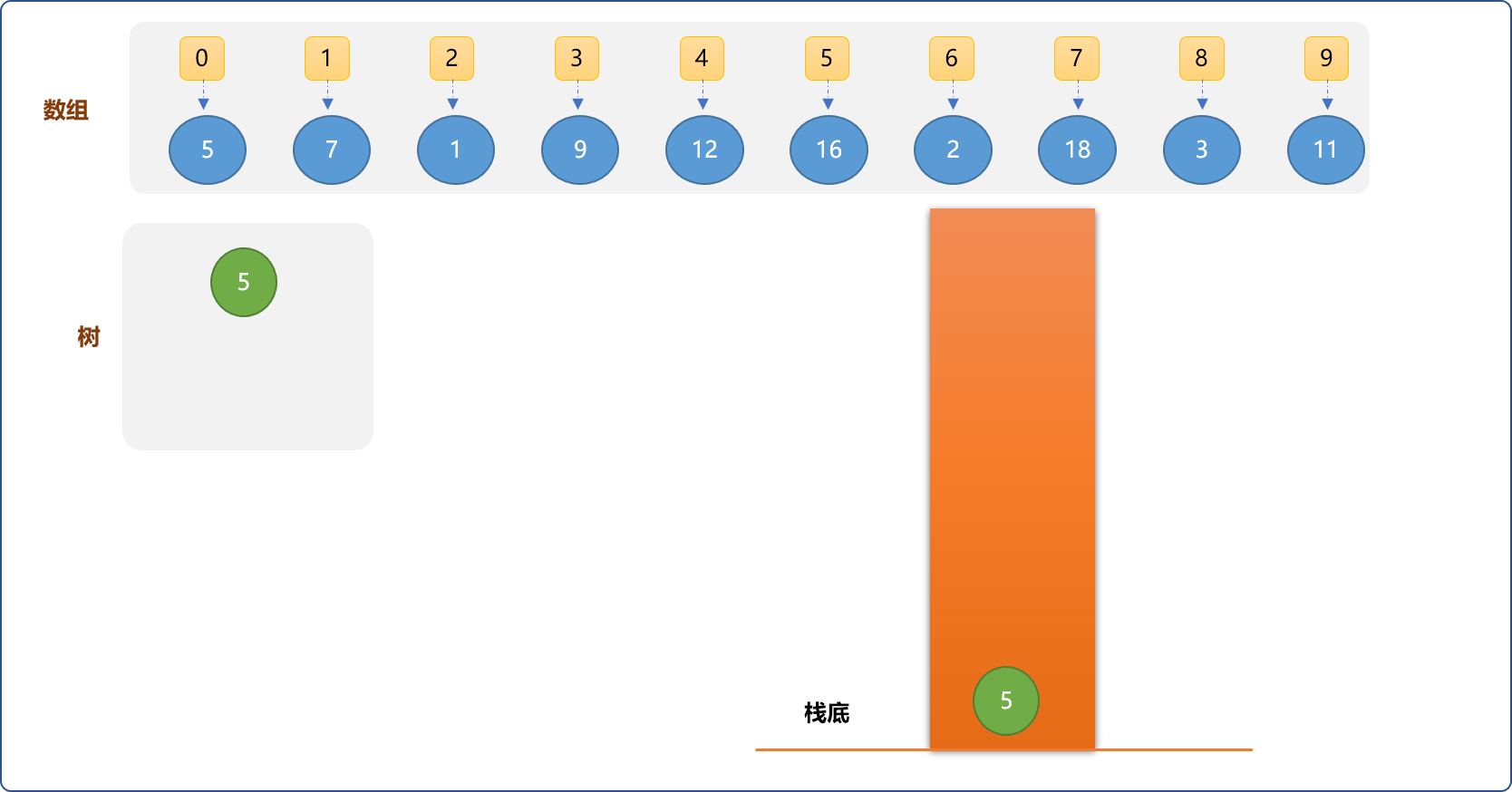
• 把数组中的(1,7)和栈中上已有元素(0,5) 比较，因值比 5 大。因能保持栈的递减顺序，可以直接入栈。且把入栈的元素作为(0,5)的右子节点。

  Tips： 至此，总结一下：能压入栈的元素作为栈中比它小的元素的右子节点。

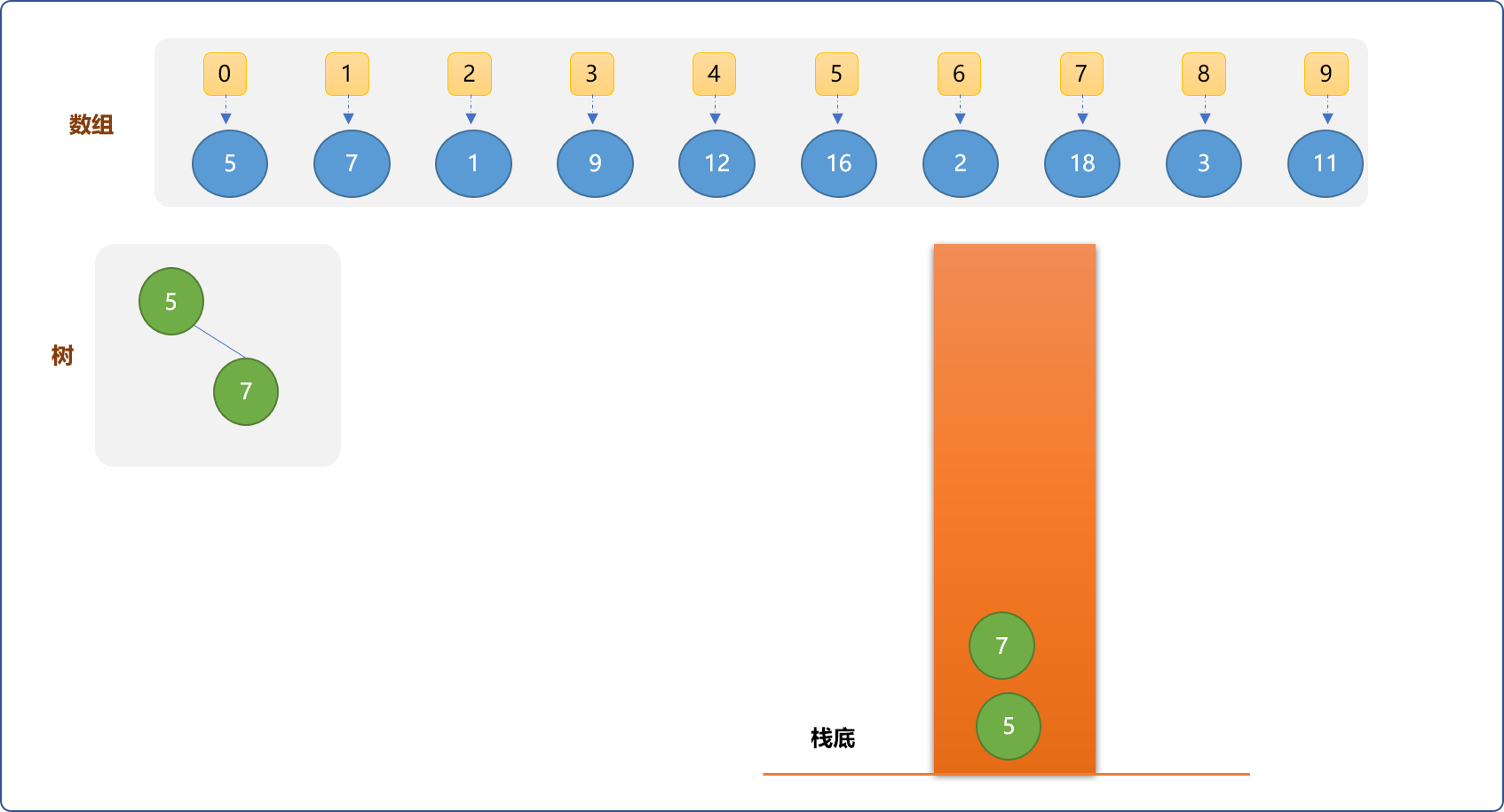
• 从数组中取出(2,1)，因比栈顶元素(1,7)小 ，不能直接入栈，则需要把比它大的元素从栈中移走，然后把最后一个比它大的元素作为它的左子结点。如下图所示：

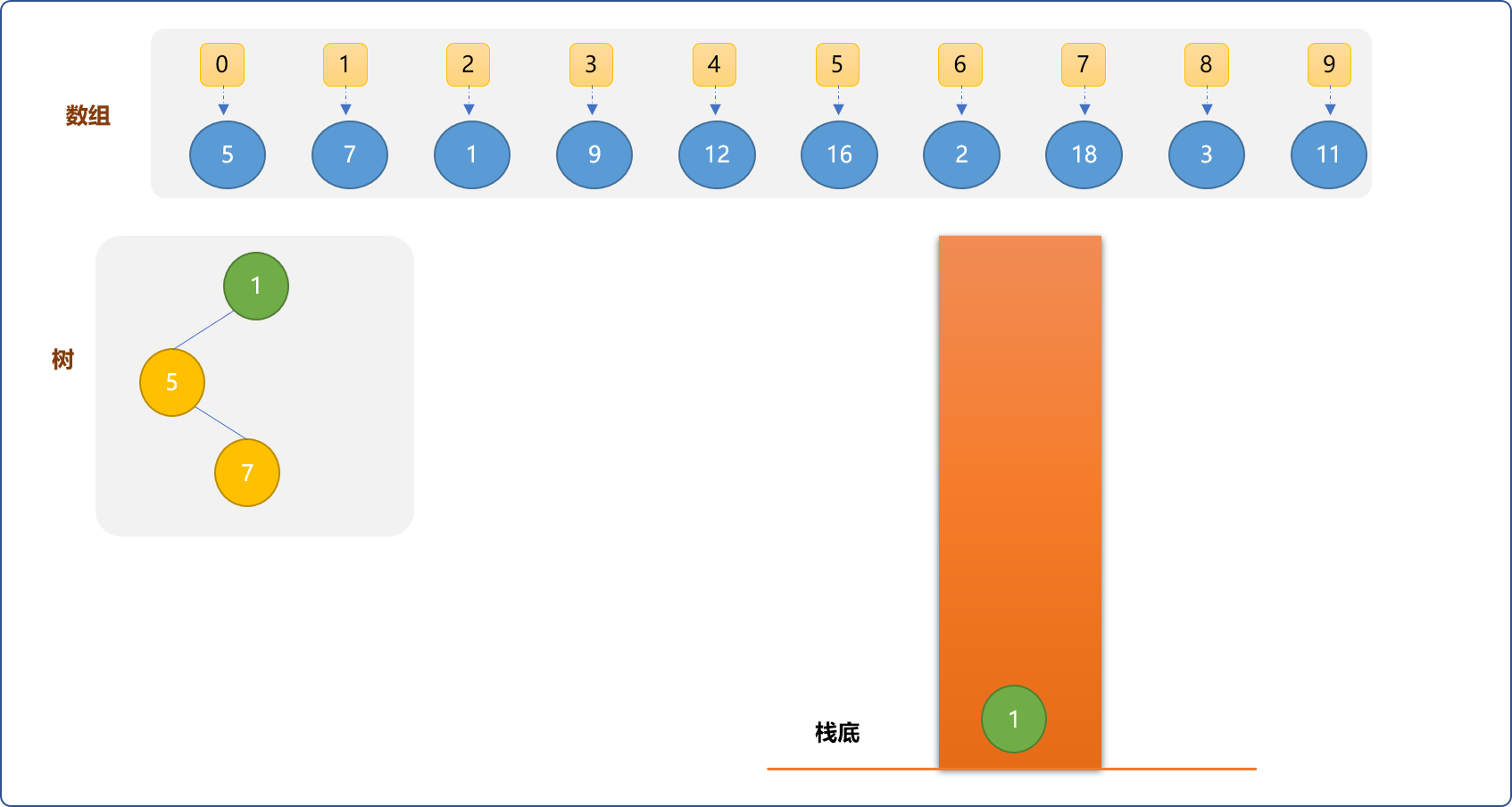
• 从数组中取出(3,9)、(4,12)、(5,16)，因都比先入栈的元素大，可以直接依次入栈，且成为比它小的节点的右子节点。

  Tips： 可以观察到，栈中的元素均为右链(图中绿色颜色所标记的节点)上的节点。

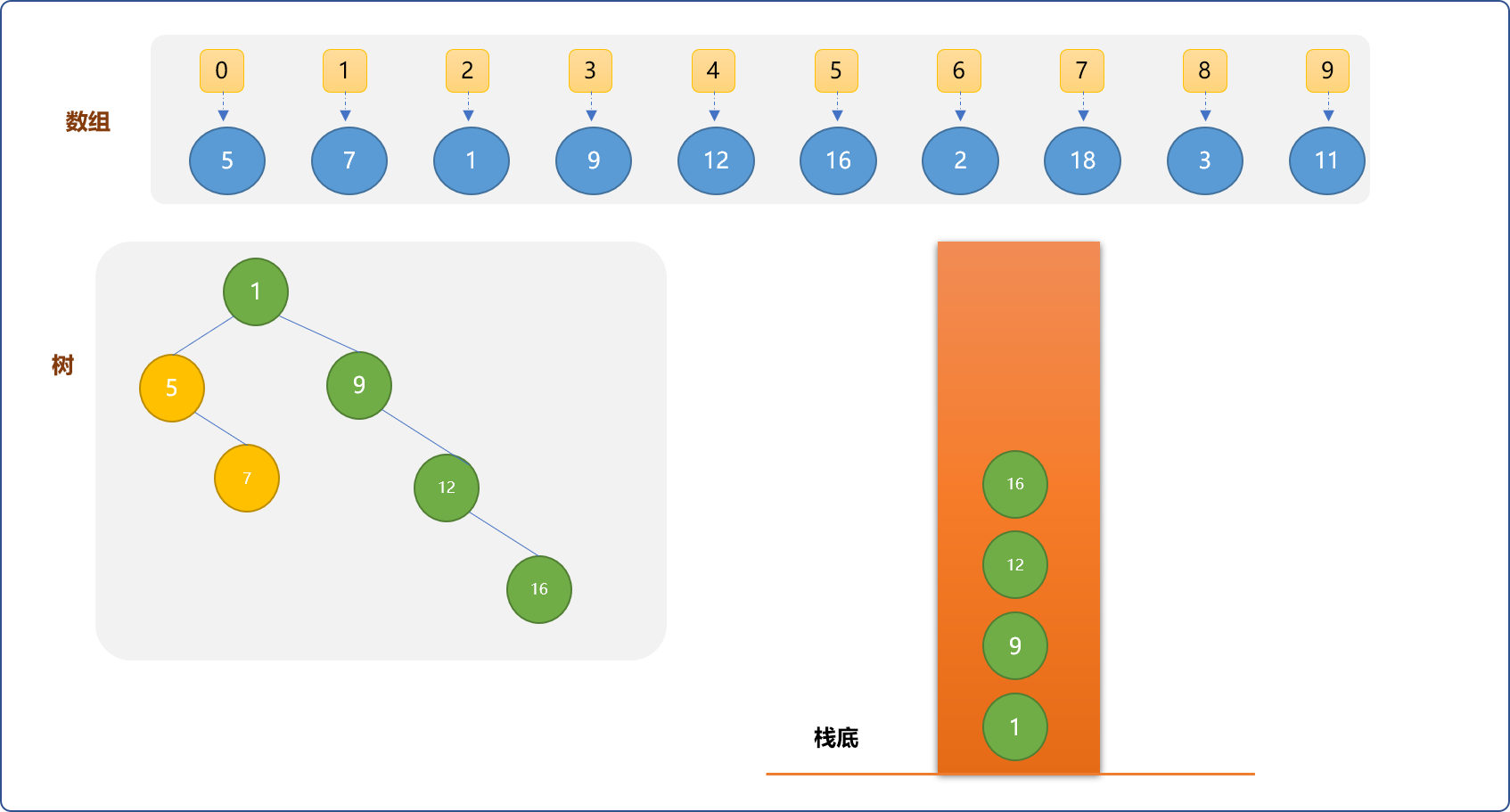
• 从数组中抽出(6,2)元素，为了维持栈的递减顺序，则需要把比它大的元素从栈中移走，直到留下(2,1)。把(6,2)作为(2,1)的右子节点，且让最后一个出栈的(3,9)成为(6,2)的左子节点。

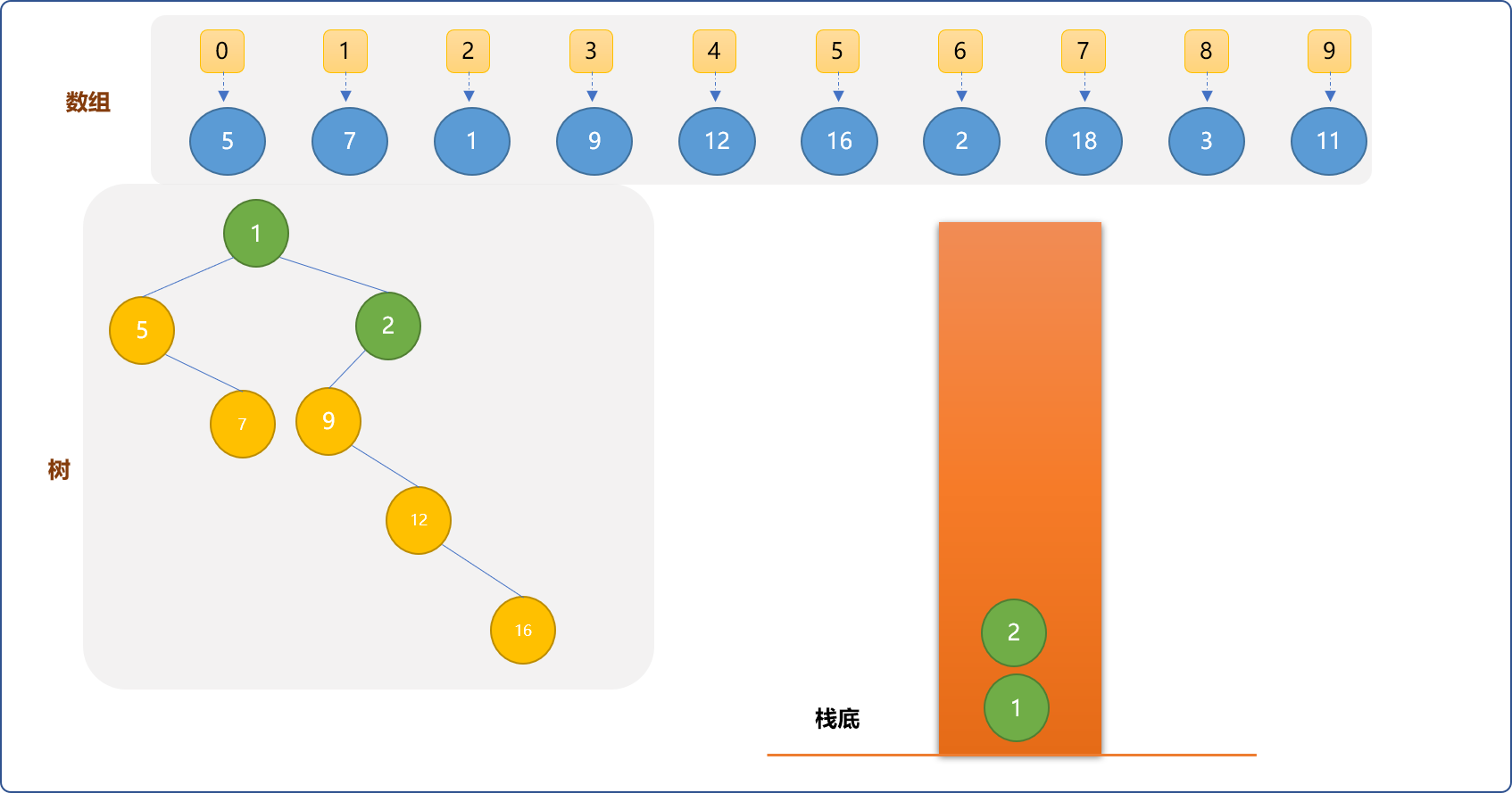
• 继续拿出(7,18)，可以直接入栈，让其成为(6,2)的右子节点。

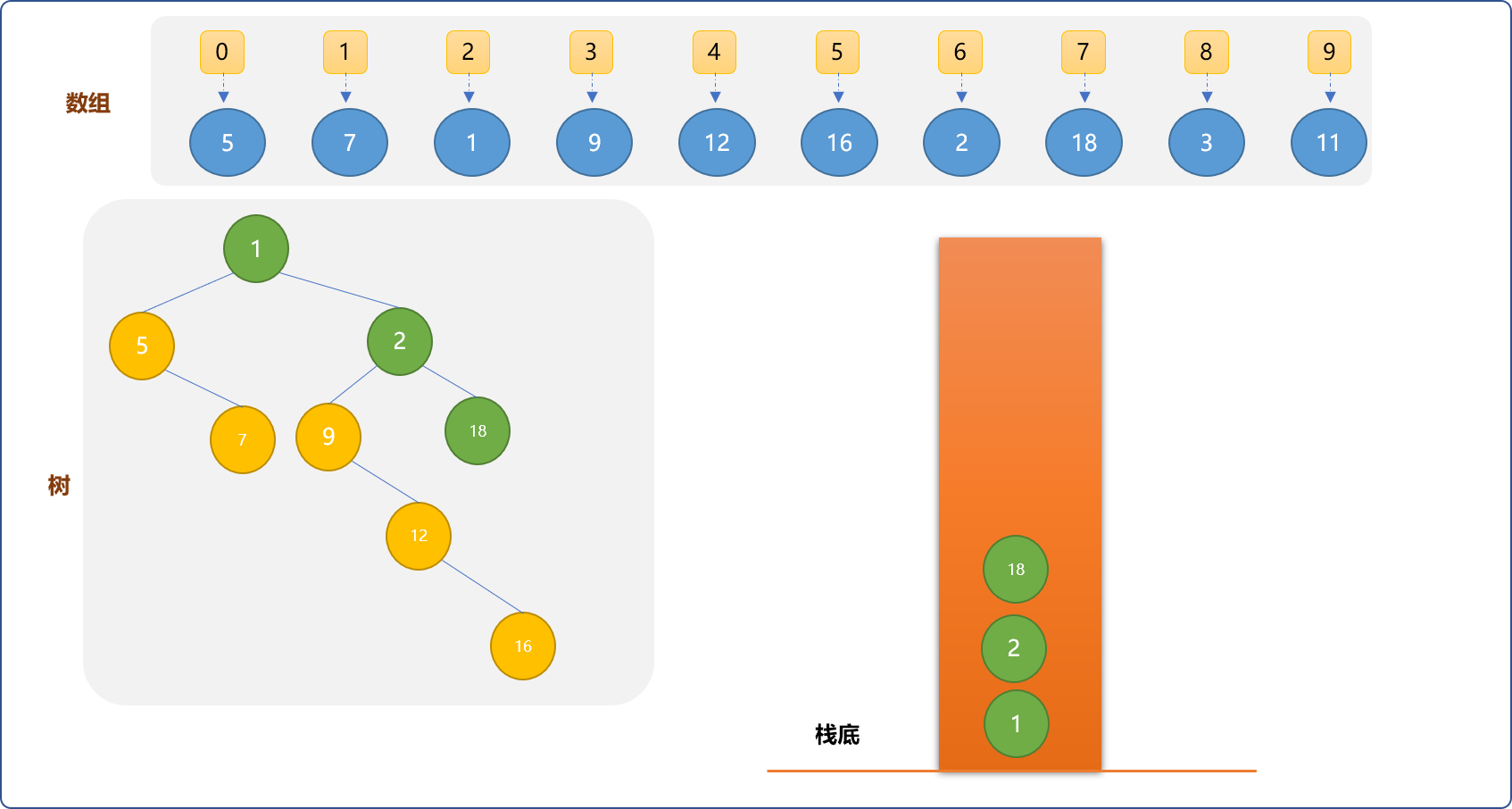
• 拿出(8,3)。把比它大的元素出栈，成为最近比它小的元素的右子结点，最后出栈的元素成为它的左子节点。

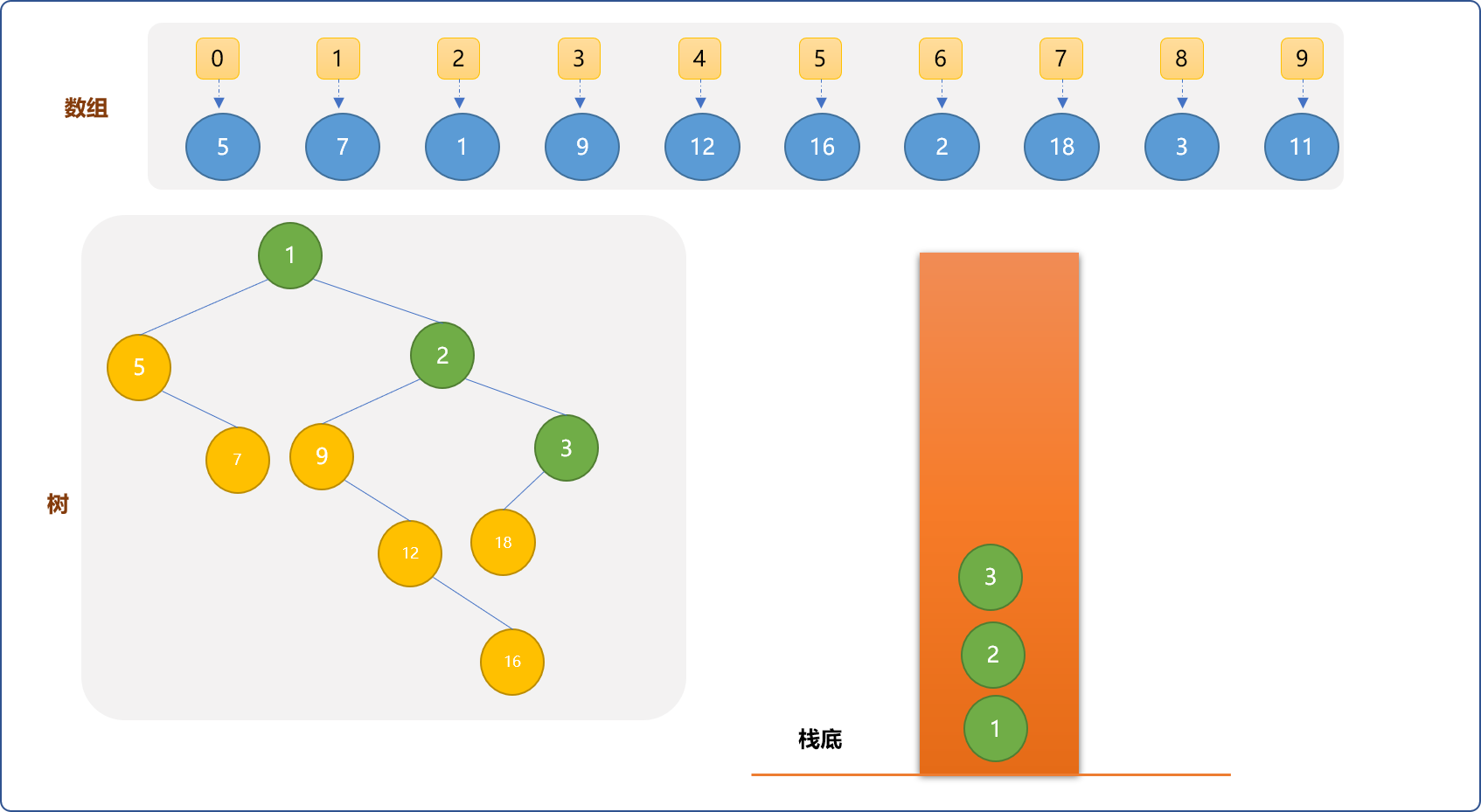
• 从数组中最后拿出(9,11)元素。因比栈中所有元素大，直接入栈，且成为栈顶元素的右子节点。

2.2 小结

使用单调栈构建笛卡尔树的原则：

• 如果需要移走其它元素后，元素才能入栈，则移走的最后一个节点成为其左子节点。
• 当数据入栈时，需要在栈中找到比它小的第一个元素，让会成为此元素的右节点。
• 栈中始终存储的最新右链上的节点。
• 构建完毕后，最后栈底的元素为根节点。

3. 笛卡尔树的物理结构

二叉树的物理实现有矩阵和链式 两种方案，本文将使用这 2 种方案：

3.1 矩阵实现

笛卡尔树类结构：

类中主要API为构建函数和中序遍历，其它的为辅助性函数。代码中有详细注解。

#include <iostream>
#include <stack>
using namespace std;
/*
*笛卡尔树类
*/
class DkeTree {
	private:
		//原数列
		int nums[10]= {5,7,1,9,12,16,2,18,3,11};
		//矩阵,描述树节点之间的关系。列号 0 表示行编号对应节点的左节点，列号 1 表示右节点
		int matrix[10][2];
		//存储元素的下标
		stack<int> myStack;
	public:
         /*
         *构造函数
         */
		DkeTree() {
             //初始化关系为 -1
			for(int i=0; i<10; i++)
				for(int j=0; j<2; j++)
					this->matrix[i][j]=-1;
		}
		/*
		* 数据入栈前的检查栈中是否有比自己大的元素
		* 参数 idx：元素在数组中位置
		* 返回最后一个比此数据大的元素编号
		*/
		int check(int idx);
		/*
		* 构建笛卡尔树
		*/
		void buildDiKeErTree();
         /*
         *中序遍历
         */
        void inOrder(int node) ;
         /*
		*返回根节点 ：栈中最后不为 -1 的元素的编号
		*/
		int getRoot() {
			int pos=-1;
			int root=pos;
			while(!myStack.empty() && (pos= myStack.top()) !=-1 ) {
				myStack.pop();
				root=pos;
			}
			return root;
		}
        /*
        *显示矩阵中节点之间的关系
        */
		void showTree() {
			cout<<"父节点"<<" 左子节点 "<<" 右子节点"<<endl;
			for(int i=0; i<10; i++ ) {
				cout<<"("<<i<<","<<nums[i]<<")->";
				for(int j=0; j<2; j++) {
					if(matrix[i][j]!=-1 )
						cout<<"("<<matrix[i][j]<<","<< nums[ matrix[i][j] ]  <<")\t";
					else
						cout<<"("<<matrix[i][j]<<","<< -1 <<")\t";
				}
				cout<<endl;
			}
		}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

实现 buildDiKeErTree 函数：

buildDiKeErTree 函数是核心API，用来构建笛卡尔树。

实现此API之前，需先实现辅助API check，用来实现把数组中的数据压入栈中时，查询到比之大的最后一个数据。本质是使用了单调栈的逻辑特性。

int DkeTree::check(int idx) {
    int pos=-1;
    //最后一个比之大的下标
    int prePos=pos;
    while( !DkeTree::myStack.empty() && (pos=DkeTree::myStack.top())!=-1 ) {
        if( DkeTree::nums[pos]<DkeTree::nums[idx] ) break;
        DkeTree::myStack.pop();
        prePos=pos;
    }
    return prePos;
}
1
2
3
4
5
6
7
8
9
10
11

buildDiKeErTree 函数：

void DkeTree::buildDiKeErTree() {
    //初始栈,压入一个较小的值，方便比较
    DkeTree::myStack.push( -1 );
    int size=sizeof(DkeTree::nums)/4;
    //遍历数组
    for( int i=0; i<size; i++ ) {
        int topIdx=DkeTree::myStack.top();
        //设置为栈顶元素的右子节点
        if(DkeTree::nums[topIdx]<DkeTree::nums[i] && topIdx!=-1) DkeTree::matrix[topIdx][1]=i;
        //从栈中移走比当前元素大的元素
        int leftIdx=DkeTree::check(i);
        if(leftIdx!=-1) {
            //置为左节点
            DkeTree::matrix[i][0]=leftIdx;
            if(DkeTree::myStack.top()!=-1)
                DkeTree::matrix[DkeTree::myStack.top()][1]=i;
        }
        //栈中存储的是数据在数组中的索引号
        DkeTree::myStack.push(i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

测试：

//测试
int main(int argc, char** argv) {
	DkeTree*  dkeTree=new DkeTree();
	dkeTree->buildDiKeErTree();
	dkeTree->showTree();
	return 0;
}
1
2
3
4
5
6
7

输出结果：-1表示不存在左或右子节点。

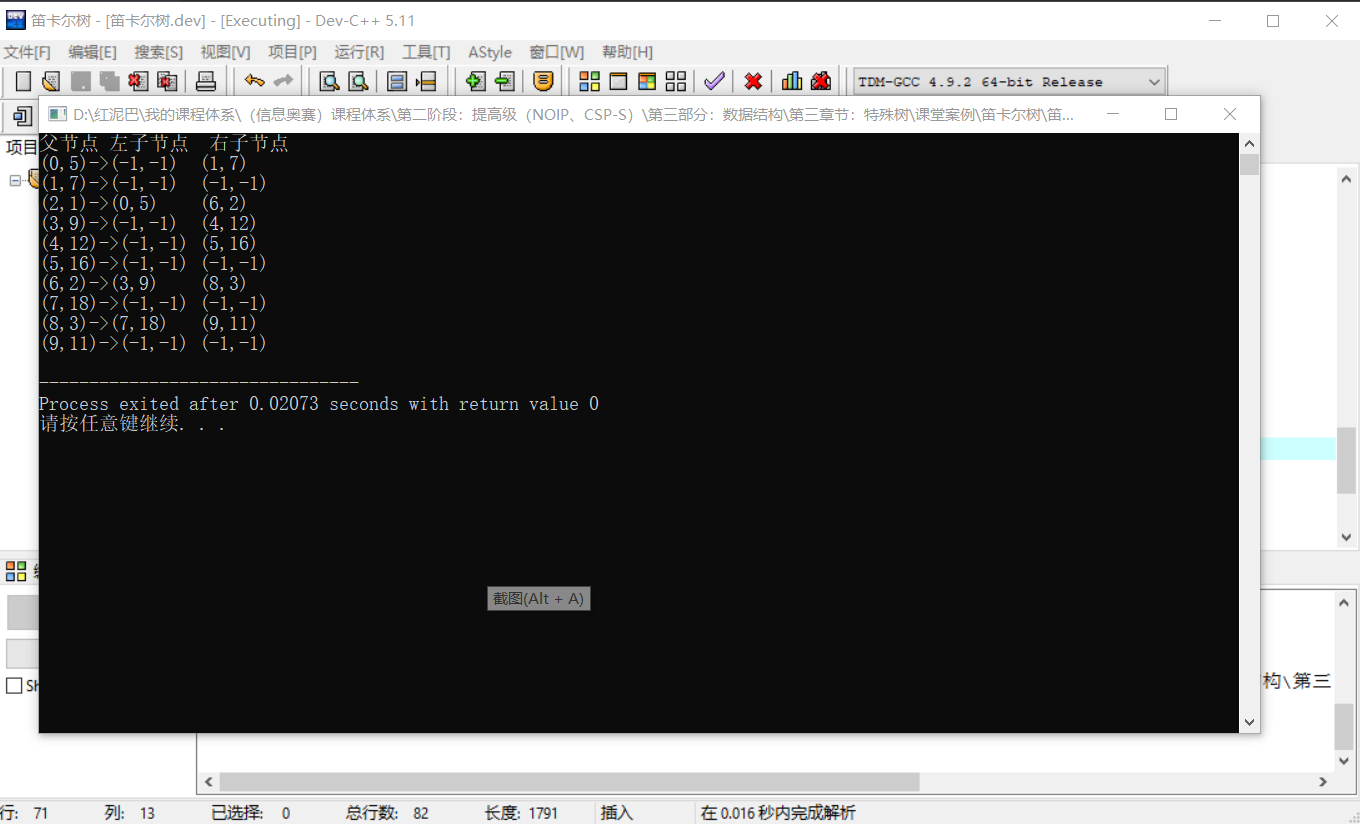
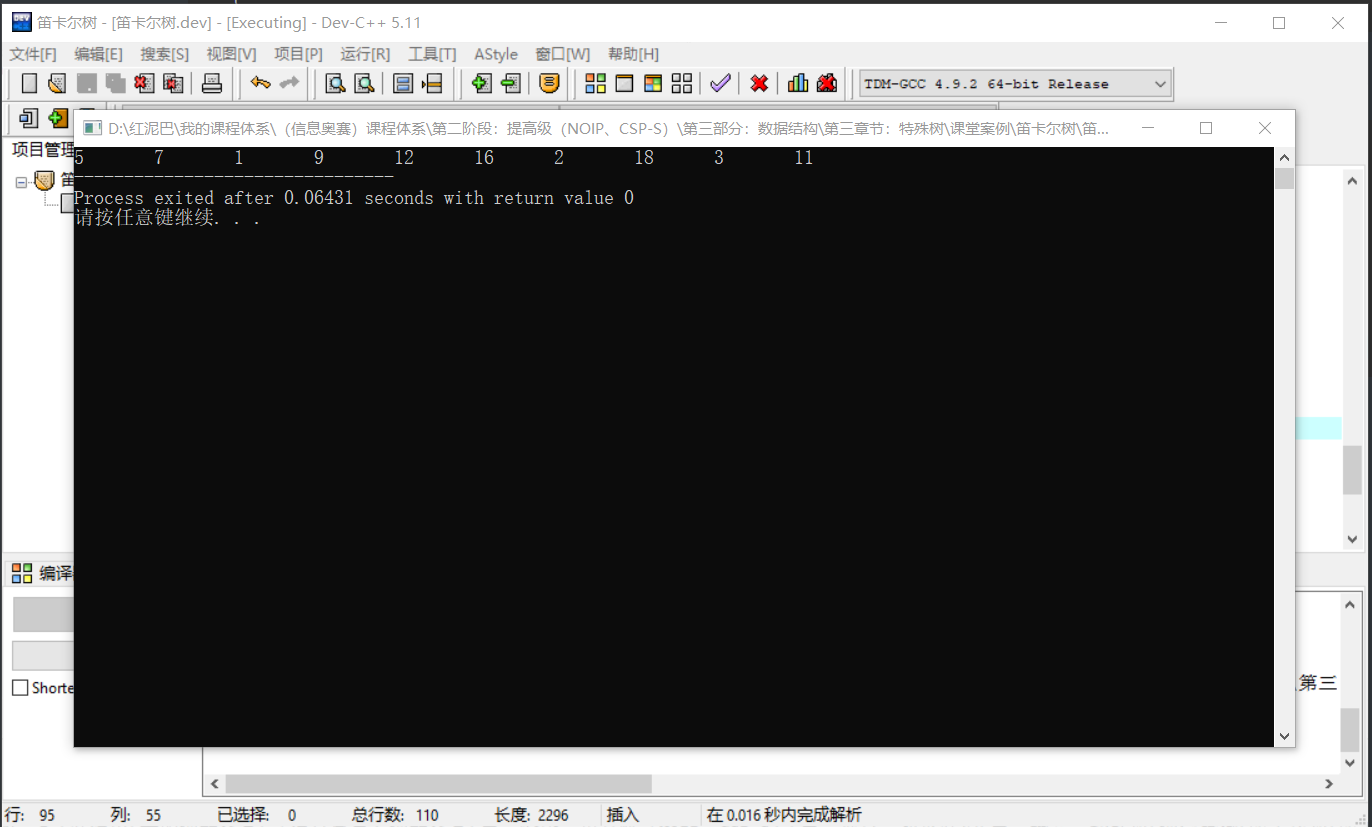
因中序遍历笛卡尔树可以输出原数组，可用于验证笛卡尔树的构建是否正确。在DkeTree类中可添加中序遍历函数的实现。

void DkeTree::inOrder(int node) {
    if( node!=-1 ) {
        //遍历左树
        inOrder(DkeTree::matrix[node][0] );
        cout<<DkeTree::nums[node]<<"\t";
        inOrder(DkeTree::matrix[node][1] );
    }
}
1
2
3
4
5
6
7
8

测试中序遍历：

int main(int argc, char** argv) {
	DkeTree*  dkeTree=new DkeTree();
	dkeTree->buildDiKeErTree();
	int root=dkeTree->getRoot();
	dkeTree->inOrder(root);
	return 0;
}
1
2
3
4
5
6
7

输出结果：

3.2 链式实现

链式实现逻辑与矩阵实现本质没有什么不一样。不做过多解释，直接上完整代码。

#include <iostream>
#include <stack>
#include <vector>
using namespace std;
/*
*节点类型
*/
struct TreeNode {
	//编号
	int idx;
	//值
	int val;
	//左子节点
	TreeNode* leftChild;
	//右子节点
	TreeNode* rightChild;
	TreeNode() {
		this->leftChild=NULL;
		this->rightChild=NULL;
	}
	TreeNode(int idx,int val) {
		this->idx=idx;
		this->val=val;
		this->leftChild=NULL;
		this->rightChild=NULL;
	}
	void show() {
		cout<<"("<<this->idx<<","<<this->val<<")";
	}
};
/*
*笛卡尔树类
*/
class DkeTree {
	private:
		//根节点
		TreeNode* root;
		//原数列
		int nums[10]= {5,7,1,9,12,16,2,18,3,11};
		//存储元素的下标
		stack<int> myStack;
		//存储树上的所有节点
		vector< TreeNode*> allNodes;
	public:
		/*
		*构造函数
		*/
		DkeTree() {}
		/*
		*  栈中查找
		*/
		int check(int idx) {
			int pos=-1;
			int prePos=pos;
			while( !myStack.empty() && (pos=myStack.top())!=-1 ) {
				if( nums[pos]<nums[idx] ) break;
				myStack.pop();
				prePos=pos;
			}
			return prePos;
		}
		/*
		* 检查树上是否存在给定的节点
		* 有：返回
		* 没有：创建
		*/
		TreeNode* findNode(int idx ) {
			for(int i=0; i<this->allNodes.size(); i++ ) 
				if( this->allNodes[i]->idx==idx )return this->allNodes[i];
			TreeNode* tmp=new TreeNode(idx,nums[idx]);
			this->allNodes.push_back(tmp);
			return tmp;
		}
        /*
        *构建笛卡尔树 
        */
		void buildDiKeErTree() {
			//初始栈,压入一个较小的值，方便比较
			myStack.push( -1 );
			int size=sizeof(this->nums)/4;
			TreeNode* node=NULL;
			TreeNode* node_=NULL;
			//遍历数组
			for( int i=0; i<size; i++ ) {
				int topIdx=myStack.top();
				//设置为栈顶元素的右子节点
				if(nums[topIdx]<nums[i] && topIdx!=-1 ) {
					node=this->findNode(topIdx);
					node_=this->findNode(i);
					node->rightChild=node_;
				}
				//从栈中移走比当前元素大的元素
				int leftIdx=check(i);
				if(leftIdx!=-1) {
					//置为左节点
					node_=this->findNode(leftIdx);
					node=this->findNode(i);
					node->leftChild=node_;
					if(myStack.top()!=-1) {
						node_=this->findNode(myStack.top());
						node=this->findNode(i);
						node_->rightChild=node;
					}
				}
				myStack.push(i);
			}
		}
		/*
		*返回根节点 ：栈中最后不为 -1 的元素的编号
		*/
		TreeNode* getRoot() {
			int pos=-1;
			int root=pos;
			while(!myStack.empty() && (pos= myStack.top()) !=-1 ) {
				myStack.pop();
				root=pos;
			}
			return this->findNode(root);
		}
		/*
		*中序遍历
		*/
		void inOrder(TreeNode* node) {
			if( node!=NULL ) {
				//遍历左树
				inOrder(node->leftChild );
				cout<<node->val<<"\t";
				inOrder(node->rightChild );
			}
		}
		void showTree() {
			for(int i=0; i<this->allNodes.size(); i++ ) {
				this->allNodes[i]->show();
				cout<<"->";
				if(this->allNodes[i]->leftChild!=NULL)this->allNodes[i]->leftChild->show();
				if(this->allNodes[i]->rightChild!=NULL)this->allNodes[i]->rightChild->show();
				cout<<endl;
			}
		}
};
/*
*测试 
*/ 
int main(int argc, char** argv) {
	DkeTree* dke=new DkeTree();
	dke->buildDiKeErTree();
	cout<<"显示所有节点"<<endl;
	dke->showTree();
	TreeNode* root= dke->getRoot();
	cout<<"中序遍历"<<endl;
	dke->inOrder(root);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153

4. 总结

本文讲解了笛卡尔树，对其特性作了较全面的分析，并且讲解了矩阵和链式两种实现方案。

本文同时收录在“编程驿站”公众号。